现代博弈论建立
现代博弈论的建立得从1944年算起,1944年冯·诺依曼的《博弈论与经济行为》以数学形式来阐述博弈论及其应用,标志着现代系统博弈理论的初步形成。冯·诺依曼被称为现代博弈论之父。
博弈论(game theory),也被称为对策论。博弈者在博弈过程中的行为(action)被称作博弈行为。
博弈行为解释:带有相互竞争性质的主体,为了达到各自目标和利益,采取的带有对抗性质的行为。
博弈论主要研究博弈行为中最优的对抗策略及其稳定局势,协助人们在一定规则范围内寻求最合理的行为方式。
博弈的要素
- 参与者或玩家(player):指的是参与博弈的决策主体。
策略(strategy):参与者可以采取的行动方案,是一整套在采取行动之前就已经准备好的完整方案。
- 某个参与者可采纳策略的全体组合形成了策略集(strategy set)。
- 所有参与者各自采取行动后形成的状态被称为局势(outcome)。
- 如果参与者可以通过一定概率分布来选择若干不同的策略,这样的策略被称为混合策略(mixed strategy)。
- 若参与者每次行动都选择某个确定的策略,这样的策略称为纯策略(pure strategy)。
收益(pay off):各个参与者在不同局势下得到的收益。
- 混合策略参与者采取的策略是按概率分布出现的,所以混合策略意义下的收益应为期望收益(expected payoff)。
- 规则(rule):指的是对参与者行动的先后顺序、参与者获得信息多少等内容的规定。
博弈论研究的基本范式
博弈论研究的基本范式:建模者对参与者(player)规定两样东西:1.可采取的策略集(strategy sets);2. 取得的收益。观察:当参与者选择若干策略以最大化其收益时会产生什么结果。最终要实现:两害相权取其轻,两利相权取其重。
囚徒困境
警方逮捕了共同犯罪的甲、乙两人,由于警方没有掌握充分证据,所以将两人分开审讯。假定条件:
- 若一人认罪并指证对方,而另一方保持沉默,则此人会被当即释放,沉默者会被监禁10年;
- 若两人都保持沉默,则根据已有的犯罪事实(无充分证据)两人各判半年;
- 若两人都认罪并相互指证,则两人各判5年。
参与者:甲、乙。
规则:甲、乙两人分别决策,无法得知对方的选择。
策略集:认罪、沉默(纯策略)。
| 乙沉默 | 乙认罪 | |
|---|---|---|
| 甲沉默 | 二人各服刑半年 | 乙被释放,甲服刑10年 |
| 甲认罪 | 甲被释放,乙服刑10年 | 二人各服刑5年 |
- 在囚徒困境中,最优解为两人同时沉默,但是两人实际倾向于选择同时认罪(均衡解)。
囚徒困境均衡解产生的原因:对两人而言认罪的收益在任何情况下都比沉默的收益高,所以两人同时认罪是一个稳定的局势。
囚徒困境表明稳定局势并不一定是最优局势。
博弈分类
合作博弈与非合作博弈
- 合作博弈(cooperative game):部分参与者可以组成联盟以获得更大的收益。
- 非合作博弈(non-cooperative game):参与者在决策中都彼此独立,不事先达成合作意向。
静态博弈与动态博弈
- 静态博弈(static game):所有参与者同时决策,或参与者互相不知道对方决策。
- 动态博弈(dynamic game):参与者所采取行为的先后顺序由规则决定,且后行动者知道先行动者采取的行为。
完全信息博弈与不完全信息博弈:
- 完全信息(complete information):所有参与者均了解其他参与者的策略集、收益等信息。
- 不完全信息(incomplete information):并非所有参与者均掌握了所有信息。
囚徒困境是一种非合作、不完全信息的静态博弈。
纳什均衡
在博弈论中有一个重要的概念:纳什均衡。
- 博弈的稳定局势即为纳什均衡(Nash equilibrium):指的是参与者所作出的这样一种策略组合,在该策略组合上,任何参与者单独改变策略都不会得到好处。换句话说,如果在一个策略组合上,当所有其他人都不改变策略时,没有人会改变自己的策略,则该策略组合就是一个纳什均衡。
- Nash定理:若参与者有限,每位参与者的策略集有限,收益函数为实值函数,则博弈必存在混合策略意义下的纳什均衡。
- 囚徒困境中两人同时认罪就是这一问题的纳什均衡。
纳什均衡的本质就是不后悔。
混合策略下纳什均衡的例子
即参与者于一定概率选择策略。混合策略纳什均衡:博弈过程中,博弈方通过概率形式随机从可选策略中选择一个策略而达到的纳什均衡被称为混合策略纳什均衡。
- 例子:公司的雇主是否检查工作与雇员是否偷懒。假定$V$是雇员的贡献,$W$是雇员的工资,$H$是雇员的付出,$C$是检查的成本,$F$是雇主发现雇员偷懒对雇员的惩罚(没收抵押金)。
- 假定$H<W<V$,$W>C$。
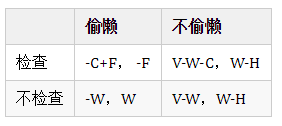
这里的参与者:
- 雇员、雇主
规则:
- 雇员与雇主两人分别决策,事先无法得知对方的选择。
混合策略集:
- 雇员:偷懒、不偷懒
- 雇主:检查、不检查
若雇主检查的概率为$\alpha$,雇员偷懒的概率为$\beta$。

由纳什均衡:其他参与者策略不变的情况下,某个参与者单独采取其他策略都不会使得收益增加。也就等价于无论雇主是否检查,雇员的收益都一样;无论雇员是否偷懒,雇主的收益也都一样。
于是有$T_{1}=T_{2}$以及$T_{3}=T_{4}$。
在纳什均衡下,由于$T_{3}=T_{4}$,可知雇主采取检查策略的概率(雇主趋向于用这个概率去检查):
$$ \alpha = \frac{H}{W+F} $$
在纳什均衡下,由于$T_{1}=T_{2}$,可知雇员采取偷懒策略的概率(雇员趋于用这个概率去偷懒):
$$ \beta = \frac{C}{W+F} $$
在检查概率为$\alpha$之下,雇主的收益:
$$ T_{1}=T_{2}=V-W-\frac{CV}{W+F} $$
对上式$W$求导,则当$W=\sqrt{CV}-F$时,雇主的收益最大,其值为:$T_{max}=V-2\sqrt{CV}+F$。
由混合策略下纳什均衡可知,雇主和雇员分别倾向于以某种概率采取策略。
我的微信公众号名称:深度学习与先进智能决策
微信公众号ID:MultiAgent1024
公众号介绍:主要研究分享深度学习、机器博弈、强化学习等相关内容!期待您的关注,欢迎一起学习交流进步!


