注:本文由不愿透露姓名的
撰写。以下为正文。
在上一篇文章中介绍了数码管如何在FPGA开发板上实现动态显示,其文章链接如下:
[走近FPGA]之数码管动态显示
本文的所有实例都使用硬木课堂Xilinx Aritx 7 FPGA板实现,且附有上板演示视频,该开发板的链接如下:
https://link.zhihu.com/?target=https://item.taobao.com/item.htm?id=612427051465
在这篇文章中,结合模块化的思想,通过分享一个二进制转BCD码的实例向大家简单介绍算法是如何在FPGA上实现的,并向大家简单介绍一种简单testbench实现自动化验证的写法。
BCD码
在数字逻辑设计课程中,我们已经学过了BCD码的相关知识,它用4位二进制数来表示1位十进制数中的0~9,是二进制编码的十进制代码,常见的BCD码有8421BCD码,2421BCD码,5421BCD码,余3码以及格雷码等等。在这篇文章中,我们所采用的BCD码为8421BCD码,8421BCD码各位的权值为8、4、2、1,用0000~1001表示十进制数,其它几种BCD码编码方式在这里不过多赘述。
二进制转BCD码(加3移位法)动态显示实例
本文实现一个二进制转十进制的电路,8位拨码开关(SW7-SW0)作为一组8位二进制输入信号,拨码开关SW11作为复位开关,拨码开关SW10作为使能开关,将8位二进制输入转为3位十进制表示,经由数码管动态显示输出。
实现这样的一个效果,可以先大致的将电路分为二进制转化和数码管显示两个部分,框架如下图所示,本篇文章主要讲述二进制转化部分。
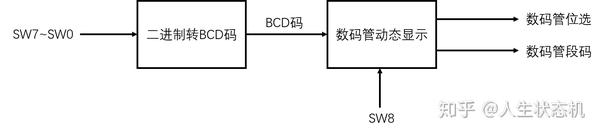
二进制转BCD码动态显示框架
二进制转BCD码看起来最简单的方法是用除法运算来获得百位、十位、个位上的值,但实际上这种方式取模会占用过多资源,底层电路设计十分复杂,这告知我们选择合适的算法对于系统是有很大帮助的,因此通常使用加3移位法实现二进制转BCD码。
在这里简单介绍一下加3移位法的原理。我们知道,四位二进制大于15才进位,而8421BCD码是大于9就进位,若四位二进制大于9时进位,这样得到的就是15的BCD码,因此将大于9的四位二进制数加6就能得到其BCD码。对于大于四位的二进制数,通过左移,逢9加6进位,即可转换任意位的二进制数,比如说,对于5位二进制数,由高4位二进制数左移一位得到,那么将前4位得到的BCD码也左移一位,并重新判断低四位是否大于9,若大于9,则加6进位,即可得到5位二进制数对应的BCD码。
加3移位法相比与加6移位法在算法上的结果是等效的,但占用的资源更小,相比于加6移位法先移位,再判断低4位是否大于9,加3移位法是先判断低四位是否大于4,再进行移位。值得一提的是,加3移位法对于最后的低4位而言无需判断低4位是否大于4,因为已经没有移位操作了。
参考网上的一个将八位二进制数255,将其转为8421BCD码的例子给大家加以说明。
0 1111 1111; //原数
1 0000 0001; //左移一次
2 0000 0011; //左移二次
3 0000 0111; //左移三次,检查低四位>4?
3.1. 0000 1010; //大于4,加3进行调整
4 0001 0101; //左移四次,检查低四位>4?
4.1. 0001 1000; //大于4,加3进行调整
5 0011 0001; //左移五次
6 0110 0011; //左移六次,检查高四位>4?
6.1. 1001 0011; //大于4,加3进行调整
7 1 0010 0111; //左移七次,检查低四位>4?
7.1. 1 0010 1010; //大于4,加3进行调整
8 10 0101 0101; //左移八次(得到BCD码255)理解了算法,接下来就是如何实现算法。实现同样功能有不同的算法,同样的,实现算法也有各式各样的电路。如何让实现的电路简单有效,就是FPGA工程师的价值所在。直白的看来,实现加3移位法,需要通过寄存器进行若干次的移位,并判断检查是否需要进位,这样“简单粗暴”实现的电路,完成一组数据的转化需要经过多个时钟周期,电路实际上也较为复杂。在这里,针对8位二进制数,我们实现的加3移位法电路结构如下图所示。
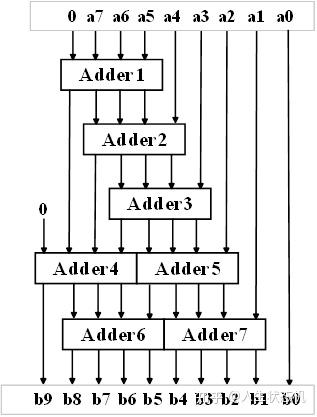
加3移位法电路
在这个电路中,Adder模块实现输入大于4就加3进位的功能,再通过人为的“移位”操作,就实现了加3移位法。具体实现过程可以理解为,首先,0和高三位(a7、a6、a5)的数据构成左移三次后的低四位二进制数据,经过Adder1模块后,得到调整后的数据;调整后数据的低三位和a4构成左移四次后的低四位数据,这四位数据作为Adder2模块的输入,就实现了“移位”,再通过Adder2进行调整数据即可;Adder3部分与Adder2部分一致,实现了左移五次的数据修正;这时,经过Adder1、Adder2和Adder3处理后的数据与a2构成了左移六次的数据,这七位有效数据的高三位可能会大于4,因而高四位和低四位都需要进行数据的调整,也就是分别通过Adder4和Adder5来修正;Adder6和Adder7与Adder4和Adder5一致,实现左移七位后的数据调整;最后,在高位填0并与最低位的a0构成最终左移八次的十二位数据。
Adder模块的功能为当输入大于4时,加3调整,当输入小于等于4时,保持原值,其电路结构如下,通过比较器,多路选择器和加法器实现功能。

Adder电路
数码管动态显示模块可以参考上一篇数码管动态显示文章加以理解,根据上一篇文章的实例一和实例二,我们可以得到这样的一个数码管动态显示模块。
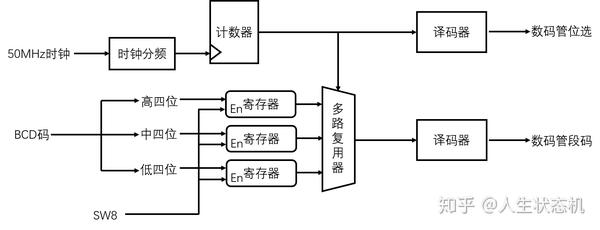
数码管动态显示电路框图
下面给出各部分RTL代码。
如下是二进制转BCD码模块的RTL代码,通过七个adder3模块以及人为的移位实现转换。
module binary2bcd(a, b);
input [7 : 0] a;
output [11 : 0] b;
wire [3 : 0] t1, t2, t3, t4, t5, t6, t7;
adder3 add1(
.x({1'b0, a[7 : 5]}),
.y(t1[3 : 0])
);
adder3 add2(
.x({t1[2 : 0], a[4]}),
.y(t2[3 : 0])
);
adder3 add3(
.x({t2[2 : 0], a[3]}),
.y(t3[3 : 0])
);
adder3 add4(
.x({1'b0, t1[3], t2[3], t3[3]}),
.y(t4[3 : 0])
);
adder3 add5(
.x({t3[2 : 0], a[2]}),
.y(t5[3 : 0])
);
adder3 add6(
.x({t4[2 : 0], t5[3]}),
.y(t6[3 : 0])
);
adder3 add7(
.x({t5[2 : 0], a[1]}),
.y(t7[3 : 0])
);
assign b = {2'b0, t4[3], t6[3 : 0], t7[3 : 0], a[0]};
endmodule
下面是adder3模块的代码,通过case语句实现功能。
module adder3(x, y);
input [3 : 0] x;
output reg [3 : 0] y;
always @ (x) begin
case (x)
4'b0000 : y <= 4'b0000;
4'b0001 : y <= 4'b0001;
4'b0010 : y <= 4'b0010;
4'b0011 : y <= 4'b0011;
4'b0100 : y <= 4'b0100;
4'b0101 : y <= 4'b1000;
4'b0110 : y <= 4'b1001;
4'b0111 : y <= 4'b1010;
4'b1000 : y <= 4'b1011;
4'b1001 : y <= 4'b1100;
default : y <= 4'b0000;
endcase
end
endmodule
接下来是动态显示的各部分代码,与上篇文章相同不赘述。
首先是时钟分频模块。
module clock_division(clk_in,divclk);
input clk_in;
output divclk;
parameter DIVCLK_CNTMAX = 24999;
reg [31:0] cnt = 0;
reg divclk_reg = 0;
always@(posedge clk_in) begin
if(cnt == DIVCLK_CNTMAX) begin
cnt <= 0;
divclk_reg <= ~divclk_reg;
end
else
cnt <= cnt + 1;
end
assign divclk = divclk_reg;
endmodule
计数器模块。
module counter(clk,cnt);
input clk;
output reg [1:0] cnt = 0;
always@(posedge clk) begin
if(cnt == 2'b10)
cnt <= 2'b00;
else
cnt <= cnt + 1'b1;
end
endmodule
寄存器模块。
module register_4bit(clk,en,data_in,data_out);
input clk;
input en;
input [3:0] data_in;
output reg [3:0] data_out;
always@(posedge clk)
if(en)
data_out <= data_in;
endmodule
三选一多路复用器模块。
module Mux(sel,ina,inb,inc,data_out);
input [1:0] sel;
input [3:0] ina,inb,inc;
output reg [3:0] data_out;
always@(*)
case(sel)
2'b00 : data_out = ina;
2'b01 : data_out = inb;
2'b10 : data_out = inc;
default : data_out = 0;
endcase
endmodule
数码管位选。
module seg_sel_decoder(bit_disp,seg_sel);
input [1:0] bit_disp;
output reg [5:0] seg_sel;
always@(bit_disp)
case(bit_disp)
2'b00 : seg_sel = 6'b111110;
2'b01 : seg_sel = 6'b111101;
2'b10 : seg_sel = 6'b111011;
default : seg_sel = 6'b111111;
endcase
endmodule
数码管段码。
module seg_led_decoder(data_disp,seg_led);
input [3:0] data_disp;
output reg [7:0] seg_led;
always@(data_disp)
case(data_disp)
4'h0 : seg_led = 8'h3f;
4'h1 : seg_led = 8'h06;
4'h2 : seg_led = 8'h5b;
4'h3 : seg_led = 8'h4f;
4'h4 : seg_led = 8'h66;
4'h5 : seg_led = 8'h6d;
4'h6 : seg_led = 8'h7d;
4'h7 : seg_led = 8'h07;
4'h8 : seg_led = 8'h7f;
4'h9 : seg_led = 8'h6f;
4'ha : seg_led = 8'h77;
4'hb : seg_led = 8'h7c;
4'hc : seg_led = 8'h39;
4'hd : seg_led = 8'h5e;
4'he : seg_led = 8'h79;
4'hf : seg_led = 8'h71;
default :seg_led = 8'h00;
endcase
endmodule
最后是顶层文件的编写,将各个功能模块例化并进行正确的连接。
module binary2bcdlight(clk,en,a,seg_led,seg_sel);
input clk,en;
input [7:0]a;
output wire [7:0]seg_led;
output wire [5:0]seg_sel;
wire [3:0]bcd1,bcd2,bcd3;
binary2bcd binary(
.a(a),
.b({bcd3[3:0],bcd2[3:0],bcd1[3:0]})
);
wire tmp_clk;
clock_division fp(
.clk_in(clk),
.divclk(tmp_clk)
);
wire [1:0] tmp_cnt;
counter count(
.clk(tmp_clk),
.cnt(tmp_cnt)
);
wire [3:0] reg_1,reg_2,reg_3;
register_4bit register_1(
.clk(clk),
.data_in(bcd1),
.en(en),
.data_out(reg_1)
);
register_4bit register_2(
.clk(clk),
.data_in(bcd2),
.en(en),
.data_out(reg_2)
);
register_4bit register_3(
.clk(clk),
.data_in(bcd3),
.en(en),
.data_out(reg_3)
);
wire [3:0] data_disp;
Mux Mux(
.sel(tmp_cnt),
.ina(reg_1),
.inb(reg_2),
.inc(reg_3),
.data_out(data_disp)
);
seg_sel_decoder seg_sel_decoder(
.bit_disp(tmp_cnt),
.seg_sel(seg_sel)
);
seg_led_decoder seg_led_decoder(
.data_disp(data_disp),
.seg_led(seg_led)
);
endmodule
借助Vivado的RTL分析功能得到对应RTL代码的电路原理图,如下图所示,能直观地看到各部分子模块及其连接方式。
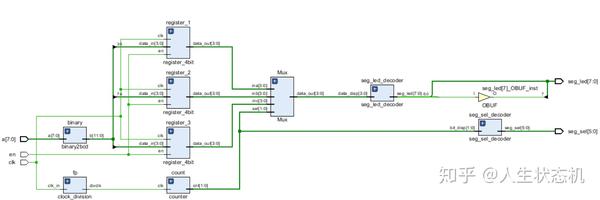
RTL分析电路原理图
在完成上述步骤后,接下来对二进制转BCD码模块进行功能仿真,验证其功能的正确性。Testbench实际上是一种验证手段,通过一种具有输入激励和输出校验的虚拟平台来进行软件层次的分析和校验。
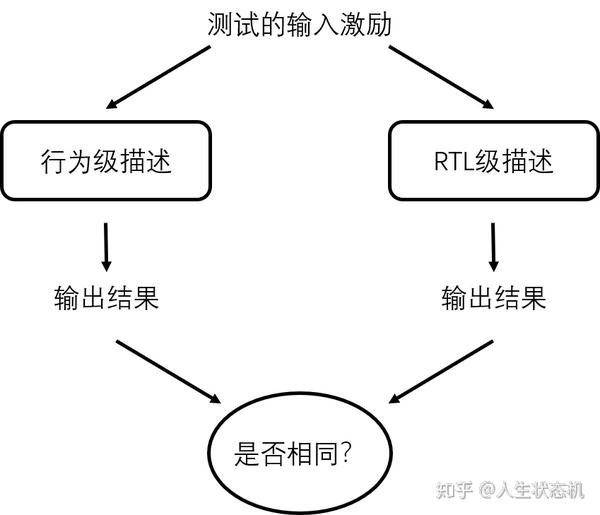
TestBench结构图
上图所示为一种简单Testbench的结构,在这个模块中行为级描述和RTL级描述是对同一功能的不同层次描述,二者的区别在于RTL级是可综合的,而行为级是为了得到结果,不关心电路结构,只注重算法,可以通过C/C++来描述。通过向两种描述方式给予足够的输入激励,就可以根据输出结果来判断我们的RTL级描述功能是否正确。
从结构图上我们也可以看出,这种结构适用于像二进制转BCD码这样直接计算的逻辑设计,但对于逻辑设计中具有复杂反馈和控制的,便需要通过UVM复杂验证框架来设计测试的结构。
下面给出Testbench模块的代码,从0不断递增1作为测试输入,来向两个描述模块进行赋值并输出结果,当二者的所有输出结果都一致时,输出“Accept”说明功能正确,否则会输出“Wrong Answer”,表明存在问题。
`timescale 1ns/1ns
module binary2bcd_tb();
reg [7 : 0] a;
wire [11 : 0] b;
binary2bcd uut(
.a(a),
.b(b)
);
initial begin : test
reg [7 : 0] i;
reg [11 : 0] b_ref;
for (i = 0; i < 255; i = i + 1) begin
a = i;
b_ref[3:0] = i % 10;
b_ref[7:4] = (i/10) % 10;
b_ref[11:8] = i/100;
#1;
if (b != b_ref) begin
$display("Wrong Answer");
$stop;
end
#9;
end
$display("Accepted");
$stop;
end
下图是Testbench在Modelsim中的仿真波形,比对输入和两种描述下的输出结果,可见两者输出一致。
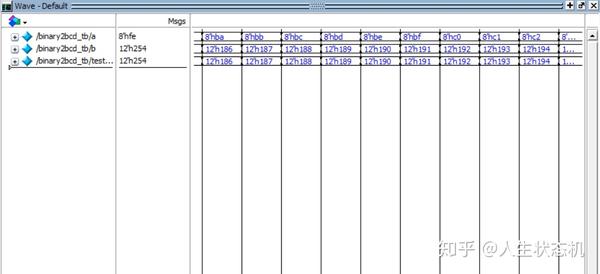
TestBench仿真波形
在Transcript窗口看到输出“Accepted”,表明电路功能正确。
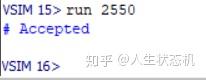
Transcript窗口输出结果
完成仿真后,就可进行后续的综合、管脚约束、布局布线以及生成比特流文件,本例具体的管脚约束如下表所示。
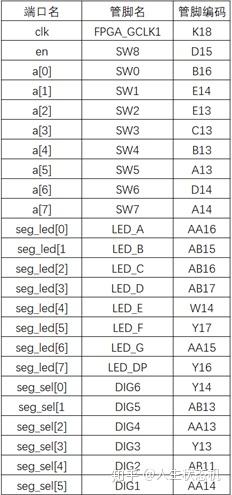
管脚约束
下面为一段该实例的上板演示视频。
实例演示视频
至此,使用加3移位法实现8位二进制转BCD码并进行动态显示的实例分享结束。在这篇文章中,借助这个实例向大家介绍了加3移位法的原理,及其如何在FPGA中得以实现,实际上实现方法有很多,而如何使得实现的电路既符合需求而又简单正是FPGA工程师的魅力所在,此外,也向大家简单介绍了一种用于没有复杂反馈和控制的逻辑设计的简单TestBench的写法。通过这篇文章,希望能够帮助大家进一步掌握模块化的思想以及理解在FPGA如何实现算法电路。
END
知乎:https://zhuanlan.zhihu.com/p/209083141
推荐阅读
- [走近FPGA]之开发板介绍篇
- [走近FPGA]之工具篇(上)-Vivado
- [走近FPGA]之工具篇(下)—Modelsim
- [走近FPGA]之组合逻辑基础
- [走近FPGA]之组合逻辑进阶——模块化设计
- [走近FPGA]之点亮LED
- [走近FPGA]之数码管动态显示
更多内容请关注其实我是老莫的网络书场专栏



