FPGA最初只是作为一种“粘合逻辑”,来实现不同芯片之间的连接和扩展。随着FPGA规模的扩大,其内部具备的查找表、乘法器、嵌入式存储器等资源逐步增加,使得FPGA具备实现需要大量运算、存储资源的数字信号处理/数值计算的能力。与之对应的是算法复杂度的也在逐步提升,对计算速度提出了更高的要求。由于FPGA内部资源较多,使用FPGA实现算法可以利用其内部查找表、乘法器等硬件实体实现并行运算,相比于纯软件实现方法通常会得到更好的性能。这是目前工程师们使用FPGA来实现算法的主要动力。但与软件方法实现算法不同,FPGA实现算法必须考虑FPGA内部硬件的连接关系、时序、控制等更为复杂的因素。受制于现在高校教育水平等诸多原因,大部分初学者对如何用FPGA来实现算法并不熟悉。因此本文介绍如何在FPGA上实现最大公约数算法,简单介绍在FPGA上实现算法的基本思想。希望通过本文的介绍,让各位朋友管中窥豹,初步形成如何用FPGA实现算法的基本概念。
辗转相除法是求解两个数的最大公约数最常用的方法,其计算步骤和正确性证明可以参考https://en.wikipedia.org/wiki/Euclidean\_algorithm。例如,计算a=1071和b=462的最大公约数的过程如下:
用1071除以462得到余数为147: 1071 mod 462 = 147
用462除以147得到余数为21: 462 mod 147 = 21
用147除以21得到余数为0: 147 mod 21 = 0
此时余数为0,所以1071和462的最大公约数为21。
下图是该过程的C++实现,输入a和b,当b不为0时,不断进行上述过程直到b为0,此时a为最大公约数。各位同学有兴趣可以自行仿真上述代码并通过单步调试观察中间过程。

辗转相除法求最大公约数的实现
在验证算法的正确性后,可以进入算法实现阶段。在FPGA上实现该算法主要有以下两个步骤,首先需要优化算法,使算法更容易在硬件上实现。之后便是将算法模型转化为RTL模型,并用硬件描述语言将模型描述出来。下面分别介绍这两个步骤。
算法优化
在上述过程中,存在使用除法求余数的步骤。用硬件实现除法开销较大,一般情况下会考虑将除法替换为其它运算操作。由于除法和减法之间存在等价关系,除法取余数本质上是不断做减法直到被除数小于除数。在这里可以首先考虑将该使用减法实现求余操作,可以使用以下方式实现辗转相除法:

使用减法实现求余操作
当a大于b时不断用a减去b,最后a的结果就是a mod b。当a小于b时则不断用b减去a,最后a的结果就是a mod b。当a等于b时,此时无论是a mod b还是b mod a都为0,因此,此时a的值即为a与b的最大公约数。
修改后的算法用减法实现取模操作,降低了硬件实现的开销。但是取模操作始终是用大的数去减小的数得到余数,因此并不需要两个减法器。如果规定a为a和b中的大数,每次取模运算都都求a mod b的值,则只需要使用到一个减法器。但这需要一个判断的步骤,在a小于b时交换a和b的值,以维护a始终大于b这一关系。按照这种思路可以写出如下代码:

用于最终实现的版本
在以上代码中,当b大于a时交换a和b,确保a永远是两个数中较大的那个数。否则不断用a减去b得到a mod b,直到b为0,此时a的值即为a和b的最大公约数。至此,我们将算法优化为更易于硬件实现的版本:首先将取模使用减法实现,再减少减法器的数量,得到了用于最终实现的版本。
简要总结一下,优化算法的目标有以下几点:
1. 减少硬件开销
2. 提高吞吐率,降低延迟
3. 降低系统功耗
而要实现这些目标主要可以考虑以下优化方向:
1. 将复杂的计算模块用简单的替换,比如使用减法算余数,但可能会带来计算时间的增加
2. 通过量化等方法减少数据位宽
3. 提高系统的并行度,增加数据处理的并发性
4. 调整计算顺序,优化计算过程以更符合硬件结构
在算法优化完成以后,下一步便是设计合适的硬件结构。
硬件结构
对于一般性的数字系统而言,其基本结构可以分为控制逻辑和数据通路两个部分。数据通路包含运算电路和保存中间结果的寄存器,用以完成对数据的处理。而控制逻辑则产生对于数据通路的控制信号,控制数据通路来完成数据处理的全过程。基于上一节得到的优化后的算法,可以设计出如下图所示的核心计算电路。
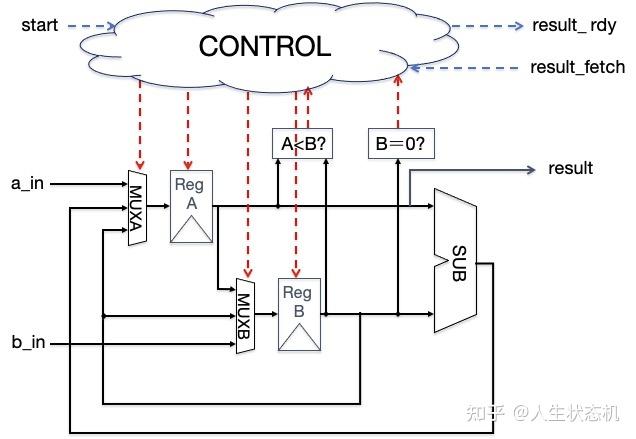
核心计算电路
图中,control部分是控制逻辑。最基本的控制逻辑可以由状态机加以实现,而复杂的控制逻辑往往需要使用微码控制器甚至于专用的微控制器等。如果系统功能进一步复杂,则需要采用SoC(片上系统)设计方法学。这部分就要看我们另外一个系列走近SoC了(虽然现在还是个大坑)。
从系统的角度看,系统的输入有数据a\_in和b\_in、start信号和result\_fetch,系统的输出则包含result\_rdy和result。设置这些信号是为了保障系统能正常运行。a\_in和b\_in为数据输入,result为计算结果,这三个输入输入是必须要配置的基本信号,无需多言。但对于一个硬件电路而言,a\_in和b\_in何时为一个有效数据,则是需要有一个信号来加以表示的。假如我们用拨码开关来实现a\_in和b\_in的数据输入,在我们拨动拨码开关的过程中显然会出现很多中间结果,这些都不是需要被计算的。只有当拨动结束,数据准备就绪以后,才需要将准备好的数据送入FPGA中加以计算。这一数据准备的过程在任何硬件电路中都是存在的,所以在这里需要使用start信号来控制计算的启动。由于计算是多次迭代完成的,在计算没有真正完成之前result上的数据其实只是一个中间结果而已。因此我们需要用result\_rdy表示一次计算是否完成,当result\_rdy输出高电平时,此时result为a\_in和b\_in的最大公约数。在有了正确的计算结果之后,下一级电路(在我们的实例中是显示电路)需要将结果取走,result\_fetch表示上一次计算的结果是否已经被取走。 当结果被取走之后电路才能重新进入就绪状态,响应下一次有效的输入。否则需要一直等待下一级电路把本次运算的正确结果取走_。_
从数据通路的角度看,数据通路需要完成算法中的几个核心操作。首先是赋值,那么需要有专门的电路来保存a和b的值。因此这里需要有2个寄存器来保存a和b的值,分别命名为Reg A和Reg B。a的值有三种赋值的可能性:最初状态时,a等于外部赋值,即等于a\_in;当a小于b时,a和b的值互换,此时a的值等于旧的b的值;当a大于等于b时,a的值等于旧a的值减去旧b的值。因此Reg A的输入需要连接一个3输入的多路复用器(MUX)来确定当前应该保存哪一个值。Reg B同样有三种情况,分为保存输入的b\_in的值,保存旧的a值以及保持不变。因此Reg B的输入同样需要连接一个3输入的MUX。
在初始状态,Reg A和Reg B分别选择a\_in和b\_in作为输入。在运算过程中,当a小于b时,MUXA选择RegB,MUXB选择RegA即可实现数据交换。否则MUXA选择a减去b的结果,MUXB选择RegB保持不变即可。为判断a是否小于b,需要用一个专门的比较器来比较二者当前的值。运算结束的标志是当前b是否已经为0,因此需要比较Reg B中保存的值和0是否相等。这两个比较器的输出信号agtb和beq0可以用于控制在运算过程中MUX的选择信号以及触发器的使能信号。
参考已有的整体架构,可以写出对于的Verilog代码来描述RTL模型。数据通路的参考代码如下:
module datapath(
input clk,
input rst_n,
input [7:0] a,
input [7:0] b,
input [1:0] sel_a, // A MUX sel
input [1:0] sel_b, // B MUX sel
input en_a, // DFF enable
input en_b, // DFF enable
output beq0, // if b = 0, beq0 = 1
output agtb, // if a > b, agtb = 1
output [7:0] res // result
);
wire [7:0] ain, bin;
reg [7:0] areg, breg;
assign ain = (sel_a == 2'b00) ? a : (
(sel_a == 2'b01) ? areg-breg : (
(sel_a == 2'b10) ? breg : 8'b0));
assign bin = (sel_b == 2'b00) ? b : (
(sel_b == 2'b01) ? areg : (
(sel_b == 2'b10) ? breg : 8'b0));
always @ (posedge clk) begin
if (~rst_n) begin
areg <= 8'b0;
breg <= 8'b0;
end else begin
if (en_a)
areg <= ain;
if (en_b)
breg <= bin;
end
end
// result output
reg [7:0] res_reg;
always @ (posedge clk) begin
if (~rst_n)
res_reg <= 8'b0;
else
res_reg <= areg;
end
assign res = res_reg;
// for control
assign agtb = areg >= breg;
assign beq0 = breg == 8'b0;
endmodule
规模较小的数字系统/子系统的控制逻辑一般采用状态机来实现。根据前述分析,对应的计算过程可以分为等待输入、计算、等待输出等三步。对应的状态图可以划分为IDLE、CALC、FINISH等三个状态。可以设计如下图所示的状态机跳转图(复位信号未在图中标出,任意时刻复位信号rst\_n有效时将跳转至IDLE状态)。
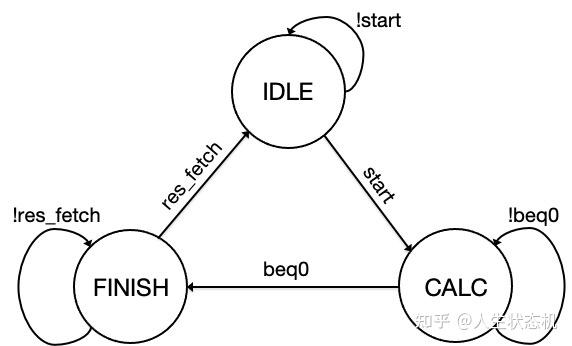
状态跳转图
系统复位后处于IDLE状态,当start信号有效时,系统跳到CALC状态开始计算。在CALC状态中需要根据数据通路中输出的agtb信号输出不同的MUX选择信号和触发器使能信号保证算法按照预定的规则持续进行。直到b等于0,beq0信号有效时跳至FINISH状态。在FINISH状态时res\_rdy将输出高电平,通知下一级此时计算已完成,可以将有效数据取走进行后续处理。输入res\_fetch信号有效时表示结果被取走,进入IDLE状态,等待下一次数据输入后启动。
参照对于状态机的规定,控制模块的参考代码如下:
module control(
input clk,
input rst_n,
input agtb, // if a > b, agtb = 0
input beq0, // if b = 0, beq0 = 1
input start, // start calculation
input res_fetch, // res fetched
output res_rdy, // result ready
output [1:0] sel_a, // A MUX select
output [1:0] sel_b, // B MUX select
output en_a, // A reg enable
output en_b // B reg enable
);
parameter IDLE = 3'b001;
parameter CALC = 3'b010;
parameter FINISH = 3'b100;
reg [2:0] cur_state, nxt_state;
always @ (*) begin
case(cur_state)
IDLE : nxt_state = start ? CALC : IDLE;
CALC : nxt_state = beq0 ? FINISH : CALC;
FINISH : nxt_state = res_fetch ? IDLE : FINISH;
default: nxt_state = IDLE;
endcase
end
always @ (posedge clk) begin
if (~rst_n)
cur_state <= IDLE;
else
cur_state <= nxt_state;
end
assign res_rdy = cur_state[2];
assign en_a = cur_state[1] | cur_state[0];
assign en_b = cur_state[1] | cur_state[0];
assign sel_a = cur_state[1] ? (agtb ? 2'b01 : 2'b10) : 2'b00;
assign sel_b = cur_state[1] ? (agtb ? 2'b10 : 2'b01) : 2'b00;
endmodule
分别描述了数据通路和控制逻辑两部分模块后,可以在顶层模块中把数据通路和控制模块连接起来。这部分在此前的专题中已经描述过多次了,不再详述。参考代码如下:
module gcd(
input clk,
input rst_n,
input [7:0] a,
input [7:0] b,
input start, // start calculation
input res_fetch, // result fetched
output res_rdy, // result ready
output [7:0] res // result
);
wire [1:0] sel_a;
wire [1:0] sel_b;
wire beq0;
wire agtb;
wire en_a;
wire en_b;
datapath dp (
.clk (clk)
,.rst_n (rst_n)
,.a (a)
,.b (b)
,.sel_a (sel_a)
,.sel_b (sel_b)
,.en_a (en_a)
,.en_b (en_b)
,.beq0 (beq0)
,.agtb (agtb)
,.res (res)
);
control ctrl (
.clk (clk)
,.rst_n (rst_n)
,.agtb (agtb)
,.beq0 (beq0)
,.start (start)
,.res_fetch (res_fetch)
,.res_rdy (res_rdy)
,.sel_a (sel_a)
,.sel_b (sel_b)
,.en_a (en_a)
,.en_b (en_b)
);
endmodule
在实现最大公约数的核心计算模块后,我们应该对其进行功能仿真以验证其正确性。下面给出简单的testbench模块:
`timescale 1ns/1ps
module gcd_tb();
reg clk, rst_n, start, res_fetch;
reg [7:0] a, b;
wire [7:0] res;
wire res_rdy;
gcd gcd_test (
.clk (clk)
,.rst_n (rst_n)
,.a (a)
,.b (b)
,.start (start)
,.res_fetch (res_fetch)
,.res_rdy (res_rdy)
,.res (res)
);
initial begin
clk = 0;
rst_n = 0;
start = 0;
a = 60;
b = 48;
res_fetch = 0;
#21 rst_n = 1;
#21 start = 1;
#10 start = 0;
#155 res_fetch = 1;
#11 res_fetch = 0;
a = 30;
b = 24;
#21 start = 1;
end
always #5 begin
clk = ~clk;
end
endmodule
在一次计算完成后,使res\_fetch信号有效,以取走当前结果,输入下一组数据,仿真波形如下图所示。
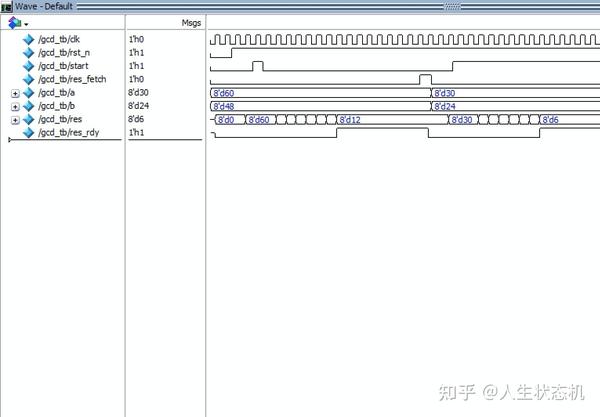
仿真波形
可以看到,res\_rdy信号有效时表示res为最终的计算结果,gcd(60,48)=12,gcd(30,24)=6,结果正确。
对核心计算单元进行初步的功能验证之后,为了便于上板调试观察,我们还需要增加一系列外围模块。本文使用拨码开关作为数据输入,矩阵键盘作为控制信号的输入,七段数码管显示结果,一个LED灯标志当前计算是否完成。
整个系统的结构如下图,输入数据a、b,当按键启动时开始计算,计算完成时输出结果res,经过二进制转bcd模块生成bcd码用于数码管显示,同时输出res\_rdy有效表示结果已经准备就绪。当我们看到数码管上显示的结果后,便可通过按键的方式“告诉”计算单元结果已被我们取走(即res\_fetch信号有效),此时计算单元状态机跳到IDLE状态,等待下一组数据输入以及启动信号start有效后开始新的一次计算。
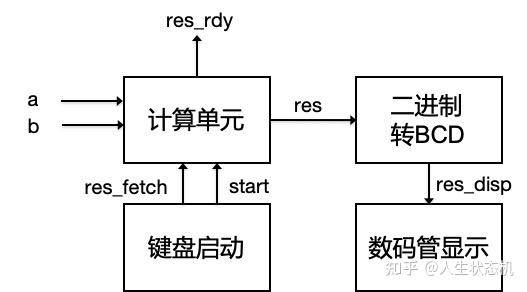
系统结构图
除计算单元以外,其他模块在本系列专栏文章里已经有过详细的介绍,所以本文不对其具体实现进行展开,可以参考以下文章:
顶层模块的参考代码如下:
module top(
input clk,
input rst_n,
input [3:0] col,
input [4:0] a,
input [4:0] b,
output row,
output [7:0] seg_led,
output [5:0] seg_sel,
output res_rdy,
output led7
);
assign led7 = 1'b0;
wire clk_1ms;
wire [3:0] key_pulse;
wire [7:0] res;
wire [11:0] res_disp;
assign row = 1'b0;
keyboard keyboard_inst (
.clk (clk)
,.rst_n (rst_n)
,.col (col)
,.key_pulse (key_pulse)
);
clk_div clk_div_inst (
.clk_in (clk)
,.rst_n (1'b1)
,.clk_out (clk_1ms)
);
gcd gcd_inst (
.clk (clk)
,.rst_n (rst_n)
,.a ({3'b0, a})
,.b ({3'b0, b})
,.start (key_pulse[3])
,.res_fetch (key_pulse[2])
,.res_rdy (res_rdy)
,.res (res)
);
binary2bcd binary2bcd_inst (
.clk (clk)
,.rst_n (rst_n)
,.en (res_rdy)
,.a (res)
,.b (res_disp)
);
wire [7:0] seg_led0, seg_led1, seg_led2;
seg_led_decoder seg_led_decoder_inst0 (
.data_disp (res_disp[3:0])
,.seg_led (seg_led0)
);
seg_led_decoder seg_led_decoder_inst1 (
.data_disp (res_disp[7:4])
,.seg_led (seg_led1)
);
seg_led_decoder seg_led_decoder_inst2 (
.data_disp (res_disp[11:8])
,.seg_led (seg_led2)
);
reg [1:0] cnt;
wire [1:0] cnt_nxt = (cnt == 2'b10) ? 2'b00 : cnt + 1'b1;
always @ (posedge clk_1ms or negedge rst_n) begin
if (~rst_n)
cnt <= 2'b00;
else
cnt <= cnt_nxt;
end
assign seg_led = (cnt == 2'b00) ? seg_led0 : (
(cnt == 2'b01) ? seg_led1 : (
(cnt == 2'b10) ? seg_led2 : 6'b111111));
seg_sel_decoder seg_sel_decoder_inst (
.bit_disp (cnt)
,.seg_sel (seg_sel)
);
endmodule
借助Vivado的RTL分析功能得到对应RTL代码的电路原理图,如下图所示。从图中能直观地看到各模块及其连接方式。
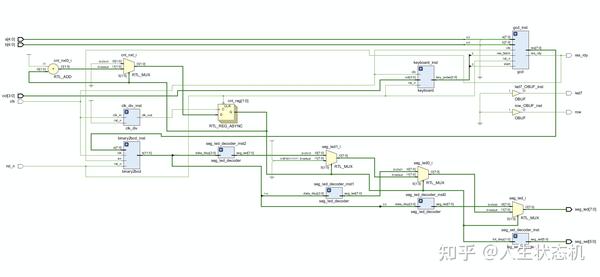
RTL分析图
接下来便是熟悉的建立工程、综合、管脚约束、布局布线以及生成比特流文件,本文介绍的例子中具体管脚约束如下表所示。需要说明的是,由于拨码开关数量有限,用于上板测试时输入a、b的位宽设置为5位。
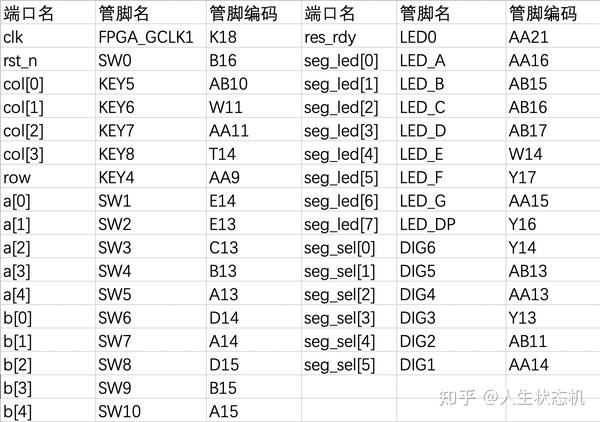
管脚约束
下面为一段该实例的上板演示视频。
GCD演示视频
至此,我们完成了最大公约数算法的FPGA实现,本文借助该例子介绍了在FPGA上实现一个算法的基本思路,首先是优化算法,使得其更容易在硬件上实现,之后便是将算法模型转化为RTL模型进行具体实现。在实际应用中,由于需求的不同,也会有不同的优化、实现方式,需要灵活变通。希望本文对读者有所帮助。
END
知乎:https://zhuanlan.zhihu.com/p/365058686
推荐阅读
- [走近FPGA]之开发板介绍篇
- [走近FPGA]之工具篇(上)-Vivado
- [走近FPGA]之工具篇(下)—Modelsim
- [走近FPGA]之组合逻辑基础
- [走近FPGA]之组合逻辑进阶——模块化设计
- [走近FPGA]之点亮LED
- [走近FPGA]之数码管动态显示
- [走近FPGA]之二进制转BCD码
- [走近FPGA]之矩阵键盘
更多内容请关注其实我是老莫的网络书场专栏



