以下有部分公式,如果无法显示,请访问原文链接
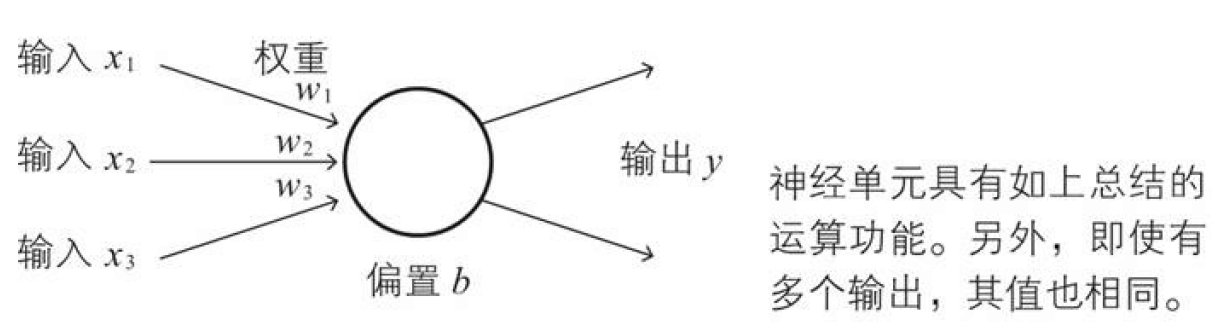
书接上文,继续说说神经网络的结构。首先我们要回顾上一篇文章深度学习数学基础(一)之神经元构造中讲到的两个公式。
- 加权输入公式
$$z=w_1x_1+w_2x_2+w_3x_3+...+b $$
- 激活公式
$$y=a(z)$$
还有神经元构造图:
我们只要将这样的神经元连接成网络状,那么就形成了神经网络。这里我们主要说最基础的阶层型神经网络,像卷积神经网络,循环神经网络等需要学习完本系列后再进行学习。
那么我们先来通俗的比喻下神经网络用来干什么的,我们以往在写程序的时候都是求结果,而神经网络求得却不是结果,而是公式或规则(比喻),其实神经网络就是通过大量的计算来不断的减小误差来求距离正解最相似的公式的权重和偏置等(统称参数)。所以感觉神经网络高大上的朋友们不要有感觉自己学不会的想法,其实神经网络并不难,就是一个又一个的公式组合起来而已,不同的算法其实就是各个大佬用数学建模,我们不看那么远,先跟我一起把神经网络的基础入门一下吧。
1 神经网络
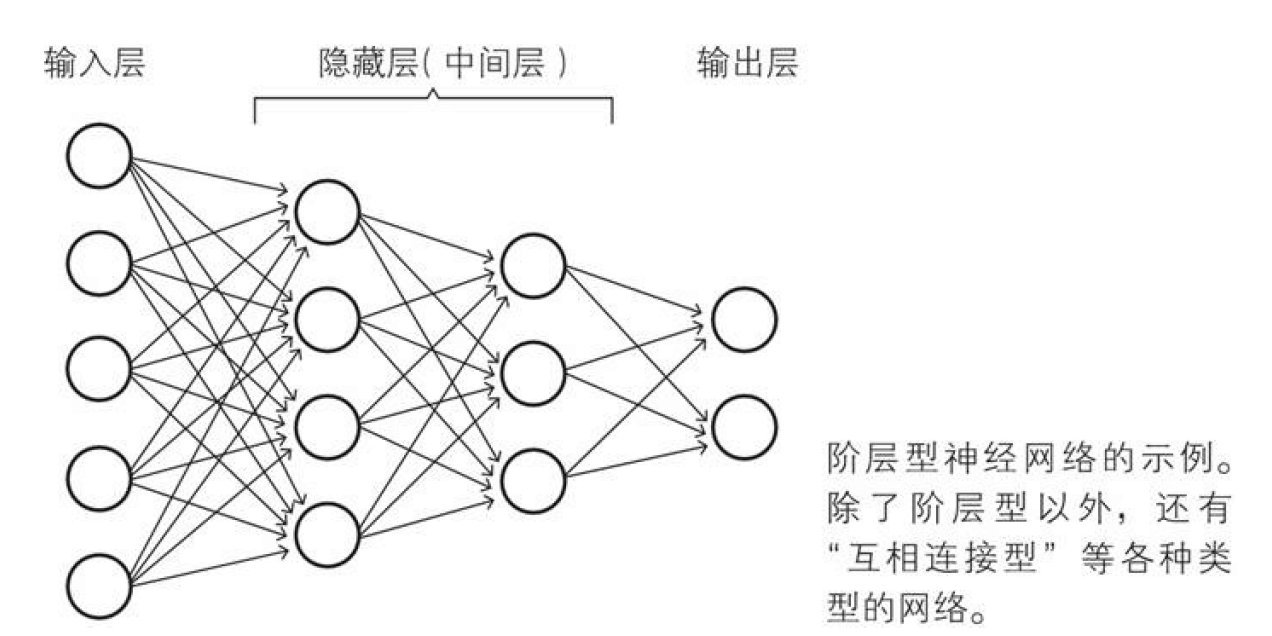
下面就是一个阶层型的神经网络的图片,按照层对该神经网络划分,可分为输入层,隐藏层(也称为中间层),输出层。
2 神经网络层级的职责
下面我们说说神经网络中各层的职责:
输入层:该层负责读取神经网络需要的数据,这个层的神经元没有输入监听,他们的输出是将读取的数据原样输出。输入==输出隐藏层:该层神经元则负责上面我们所回顾的两个公式的计算操作,在神经网络中,这层是实际处理信息的部分。计算z和y输出层:该层与隐藏层一样,执行两个公式的计算,并且显示神经网络的计算结果,也就是最终输出。计算z和y并显示结果
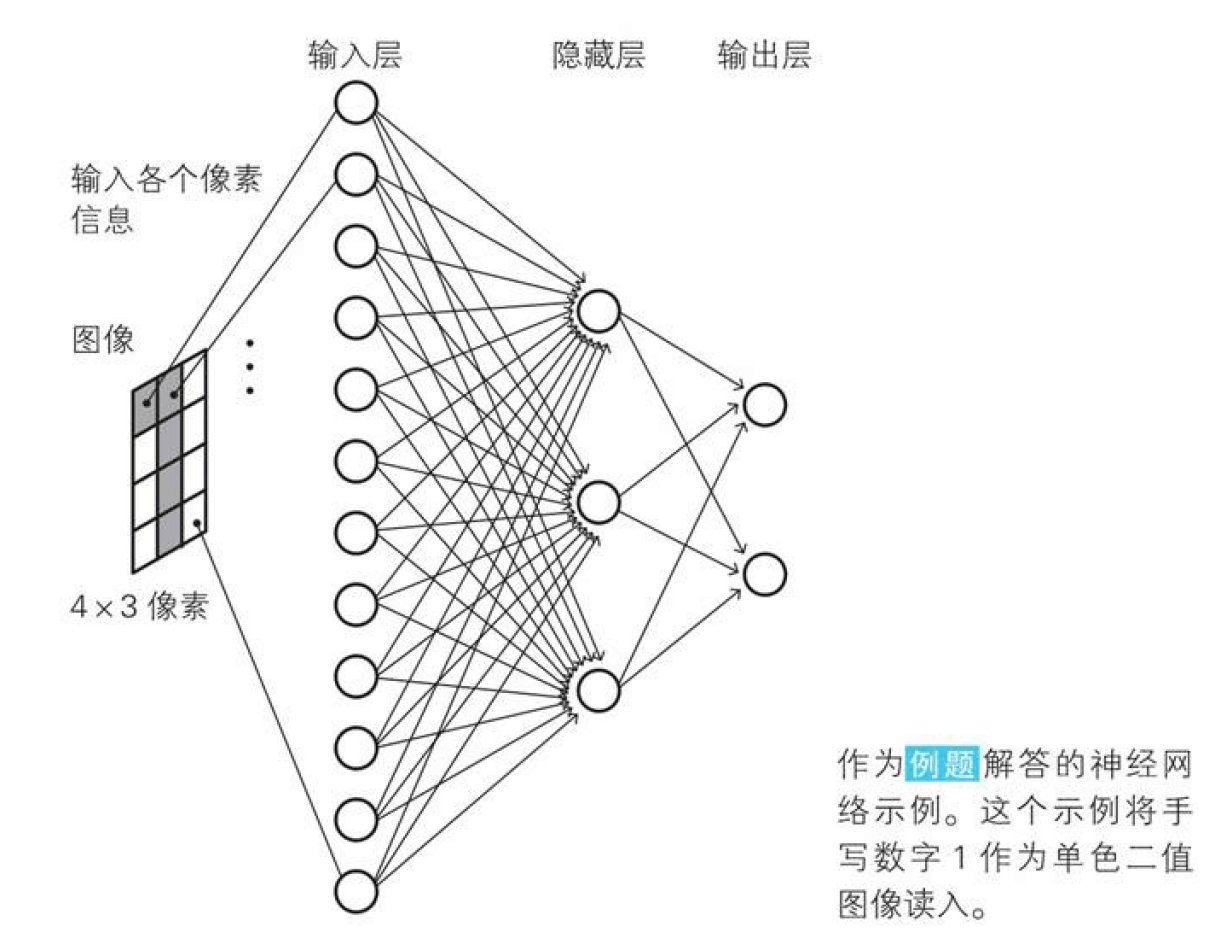
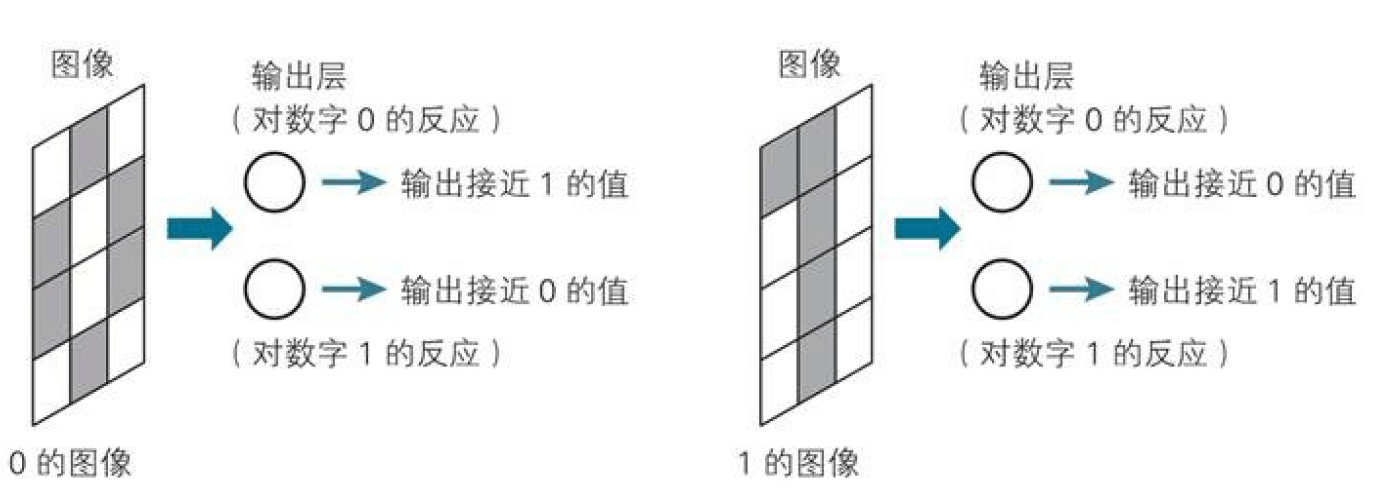
下图是一个最简单的神经网络示例,用于我们来理解神经网络的本质。这个简单的神经网络的特征是,前一层的神经单与下一层的所有神经元都有箭头连接,这样的层构造称为全连接层(fully connected layer)
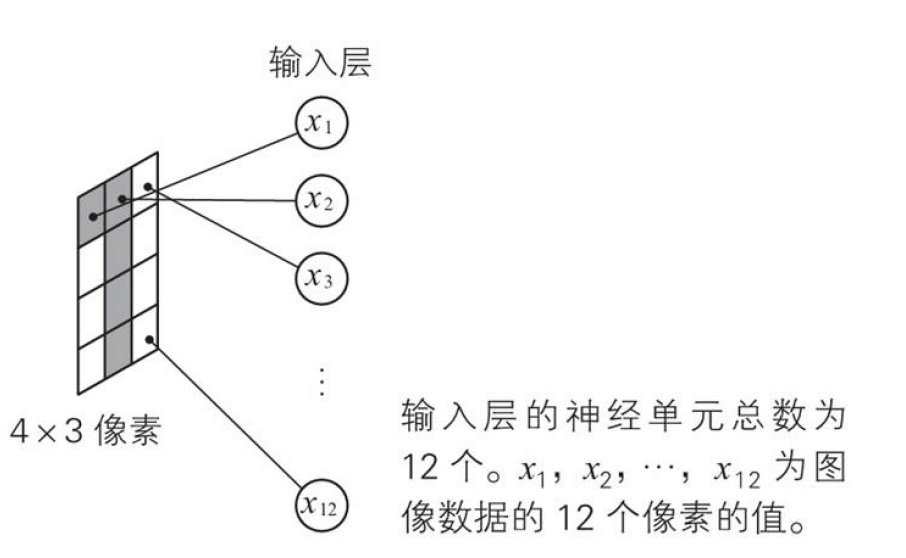
输入层:输入与输出是相同的,如果一定要引入激活函数,那激活函数就是恒等函数$a(z)=z$,该示例中输入层有12个神经元,对应图片的12个像素数据
隐藏层:输入是变量,根据对应的权重和偏置来计算z,再经由激活函数计算,输出值传递到下一层
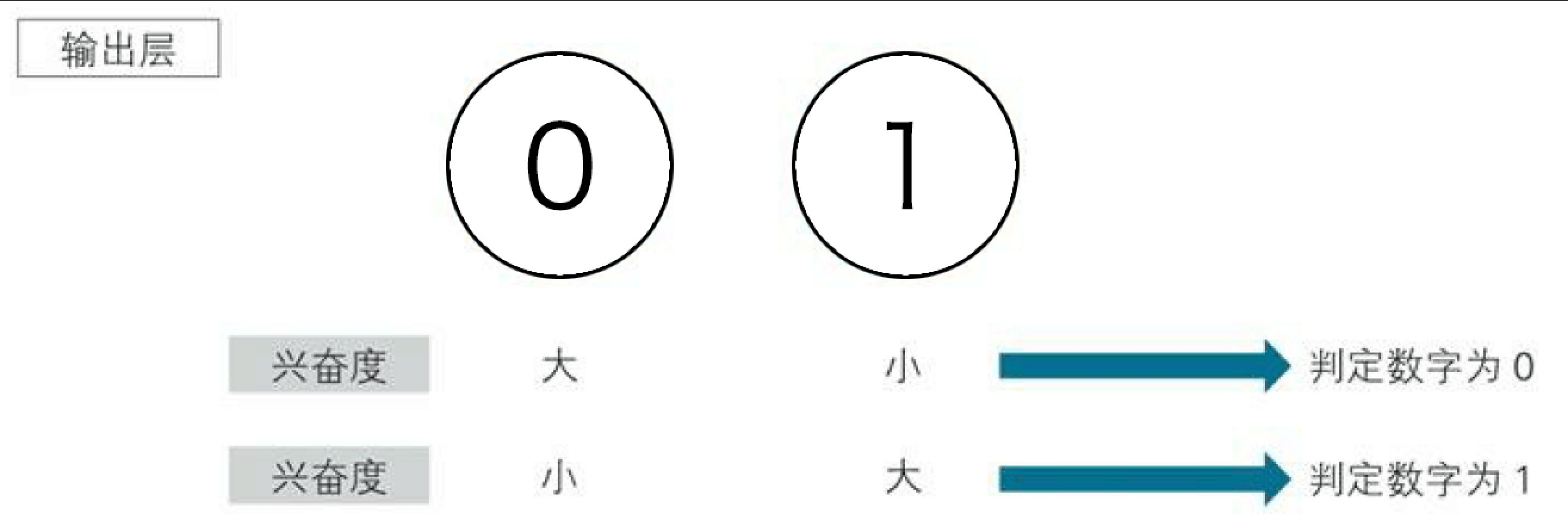
输出层:该层有两个神经元,分别对应着要识别的数字0和1,两个神经元分别是对两个输出值较为兴奋的神经元,通过sigmoid我们可以拿到两个神经元对数据的兴奋度,通过对连个兴奋度做比较,我们就可以来猜这个数据到底是什么了!
3 神经网络的结构
3.1 示例说明
我们还使用上方的示例来进行说明
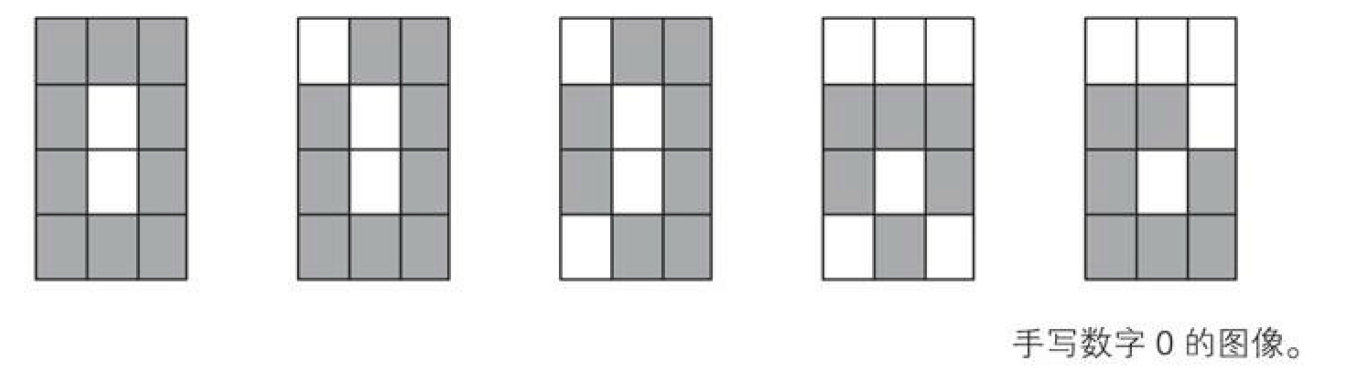
建立一个神经网络,用来识别通过 4×3 像素的图像读取的手写数字 0 和 1。学习数据是 64 张图像,其中像素是单色二值。
模式识别的难点在于答案不标准,这个例题也体现了这样的特性。即使是区区一个 4×3 像素的二值图像,所读入的手写数字0 和 1 的像素模式也是多种多样的。例如,上方图像可以认为是读入了手写数字 0。对于这样的数字 0,即使人能设法识别出来,让计算机来判断也十分困难。下面让我们使用一个小故事来了解下如何使用神经网络来解决这个问题。
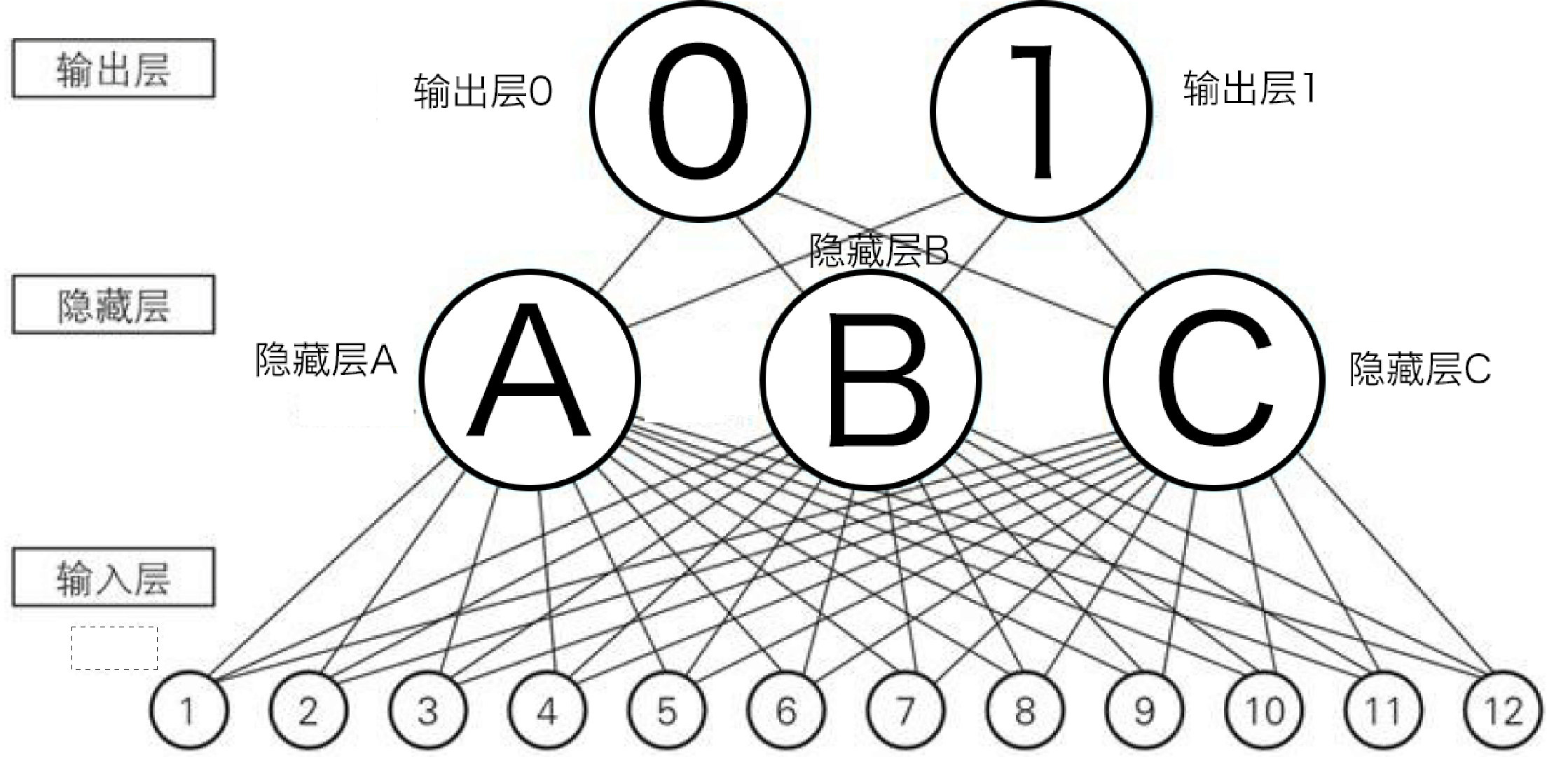
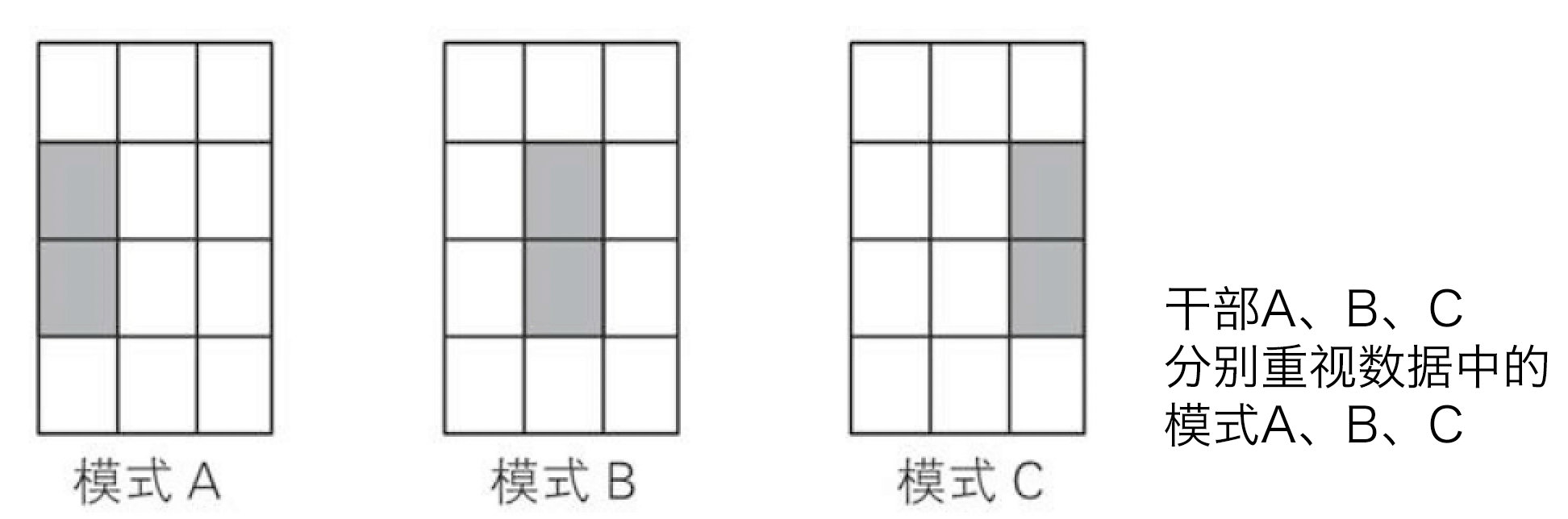
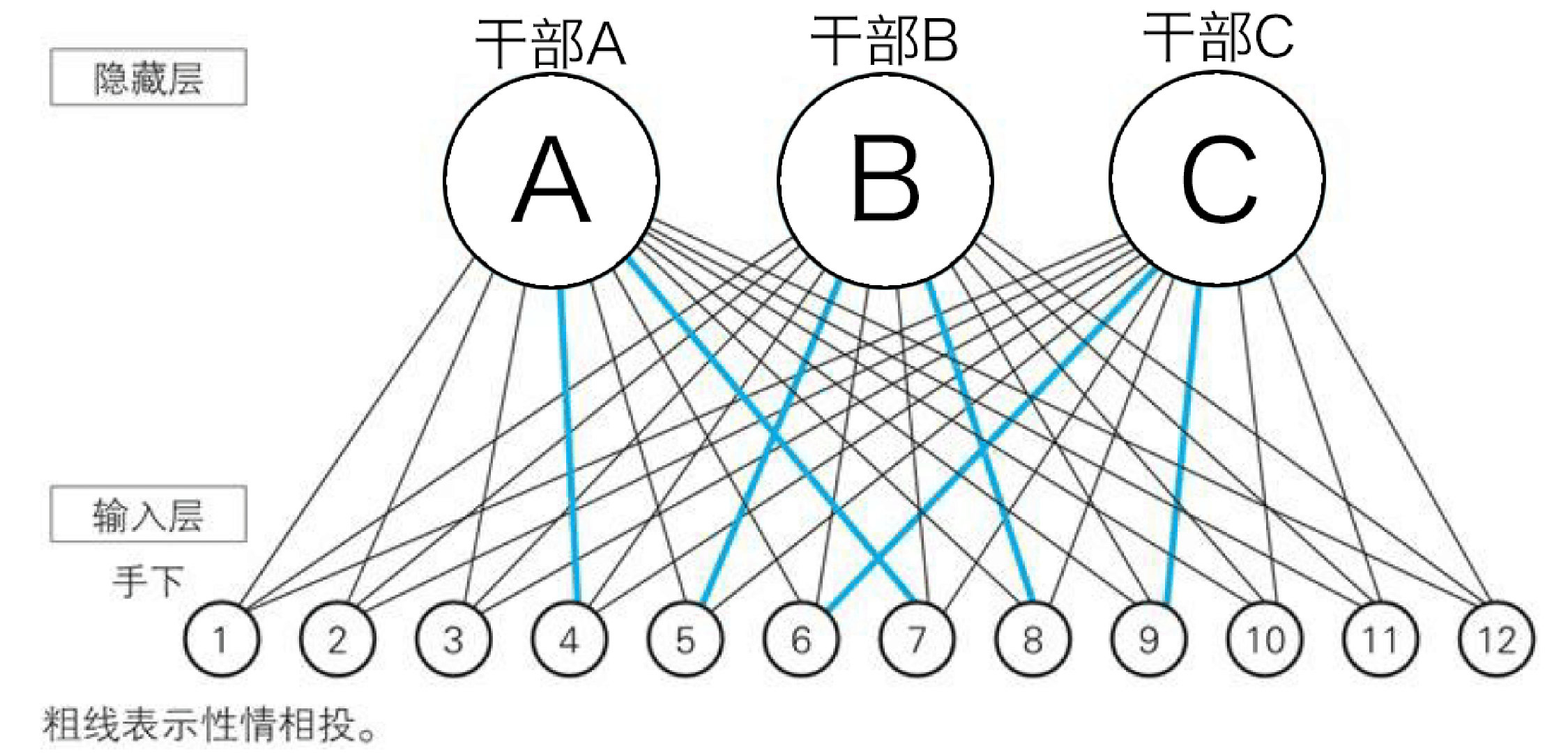
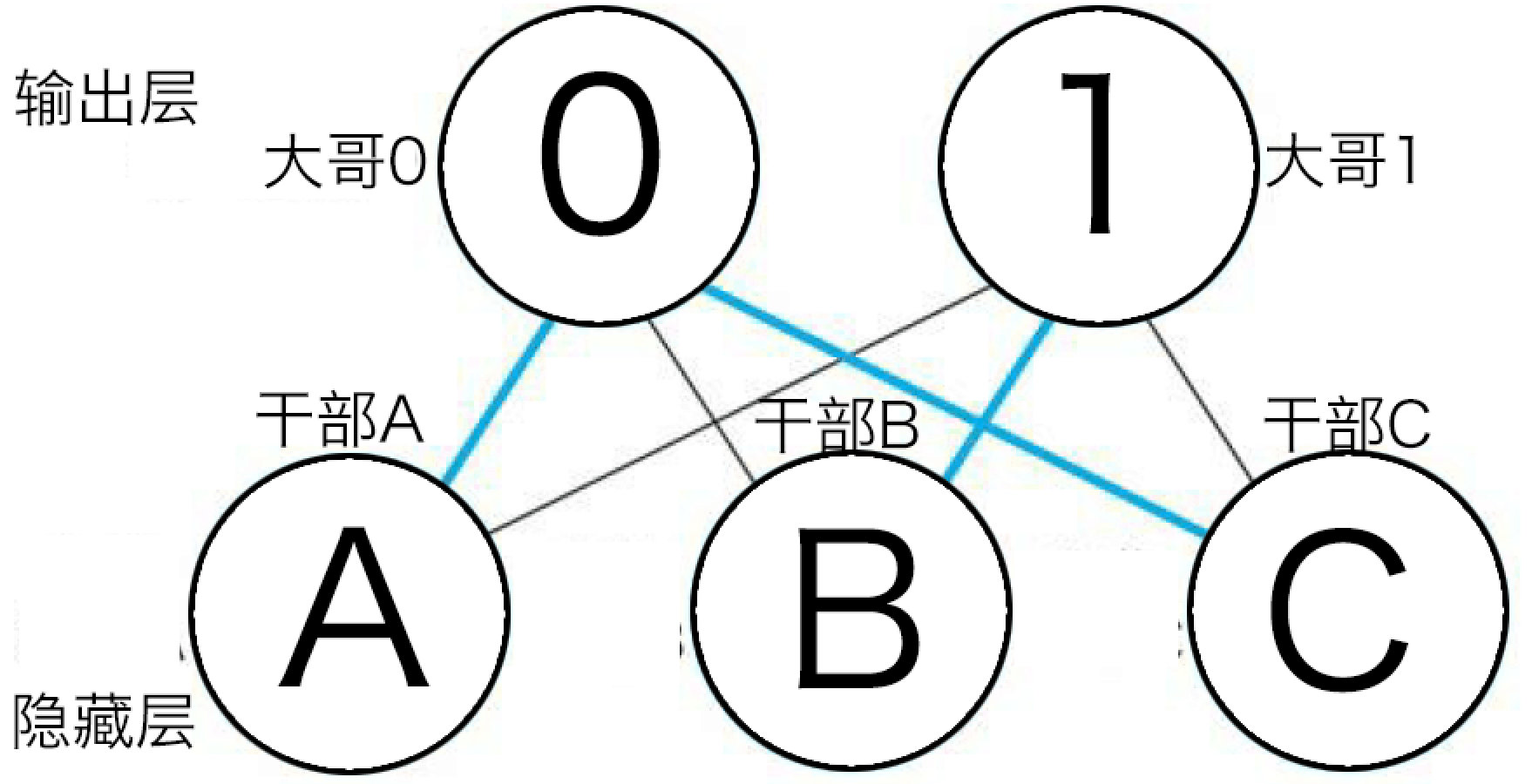
假设有个神经网络,输入层12个神经元小弟,隐藏层住着3个神经元中层干部,顶层住着2个神经元大哥,
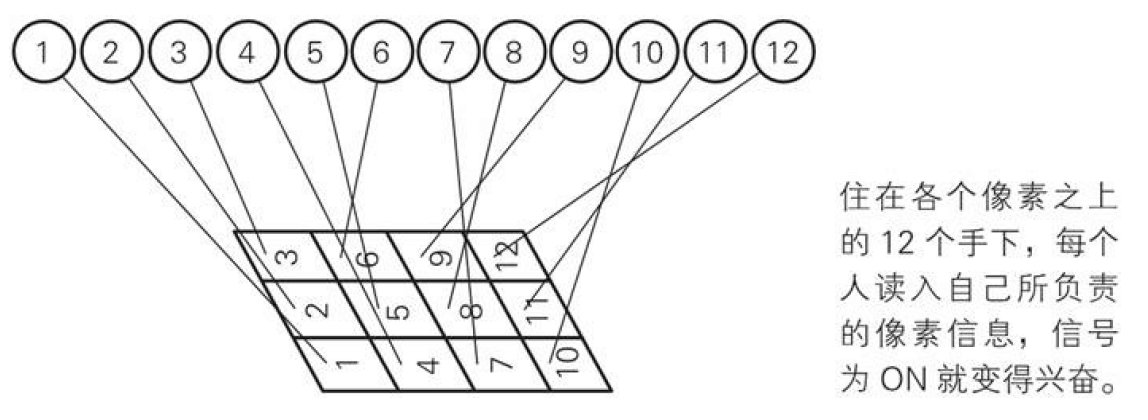
底层输入层的12个小弟接到任务要监控图片的动静,所以12个输入层小弟分别住在4x3像素的图像的各个像素上对图片进行监控,如果像素信号是白色0,小弟就睡觉不管,如果像素是黑色1,小弟就兴奋向上层通风报信,将他们的信息传递个他们的领导A、B、C
住在隐藏层的3个中层干部ABC分别重视下面三个地方,从下面的小弟那里拿到信息,然后自身对信息的思考(计算z和y),看看有没有需要自己注意的地方,把自己的想法跟顶层的两个大哥汇报
住在最顶层输出层的大哥拿到下面三个干部递交的信息,与三个干部一样,也进行了思考作出了对应的策略,然后两个大哥看了下各自的策略,选出更好的那一个(兴奋度高的)作为了这次行动的策略。
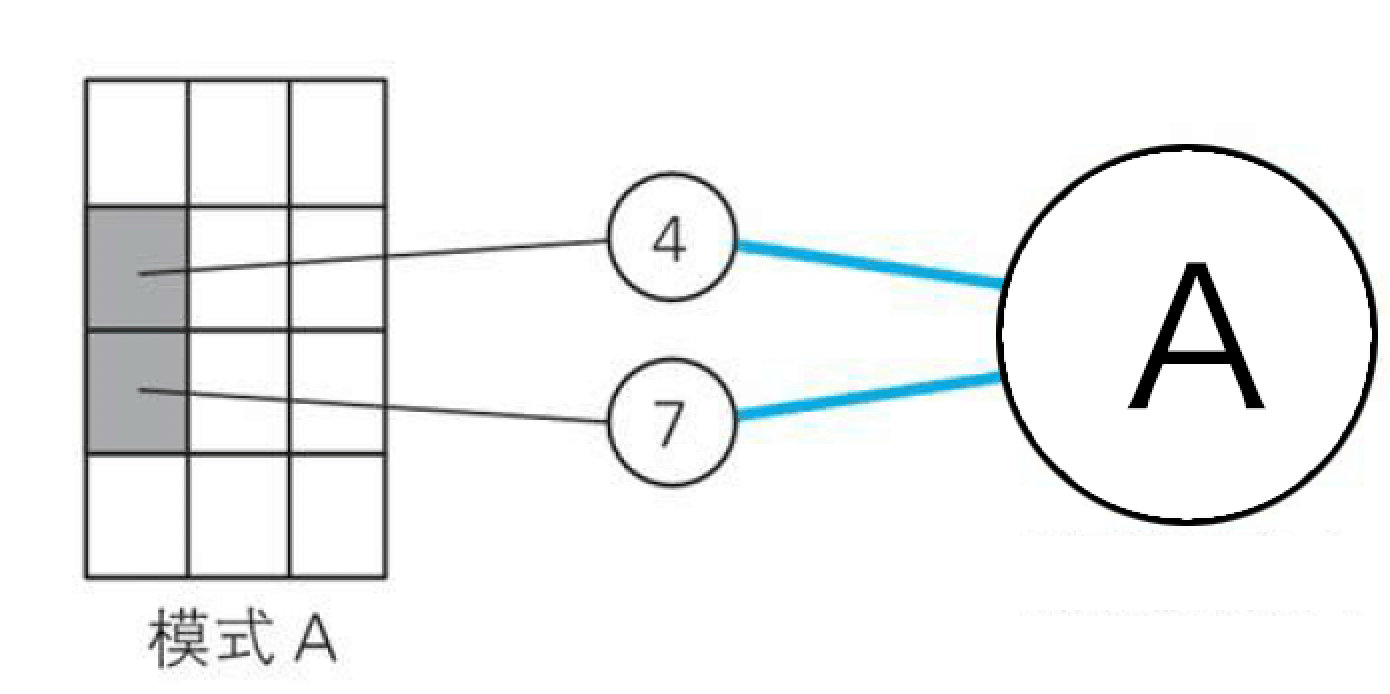
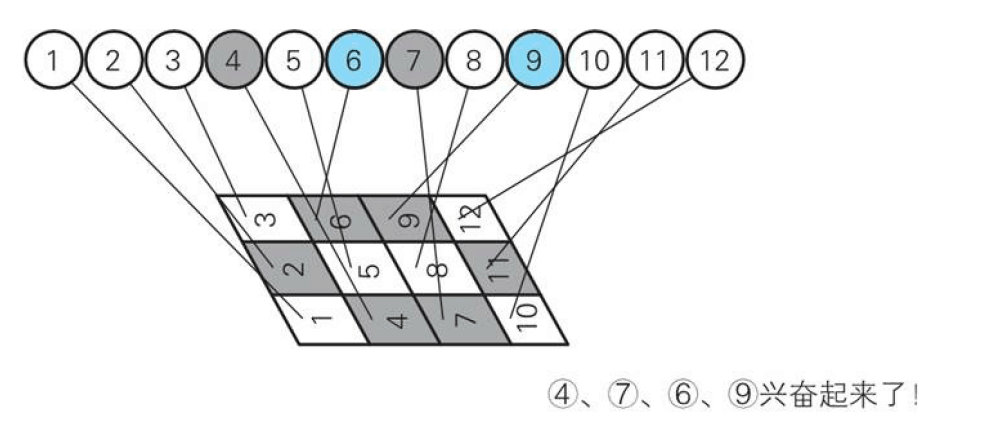
让我们再来回顾下上面说到的隐藏层,3个中层干部分别重视三个模式,所以3个中层干部对12个手下各有偏爱,比如A干部就看重小弟4和7,B干部看重小弟5和8,C干部看中小弟6和9。
所以这几个干部有点偏心,着重看了直接小弟给的情报,所以他们之间传递的兴奋度的管道也变粗了。
而住在顶层的大哥对中层的干部也各有偏爱,比如大哥0喜欢干部A和C,大哥1喜欢干部B
那么,我们读入手写数字0,下面的小弟4、7、6、9看到这个图就特别兴奋了
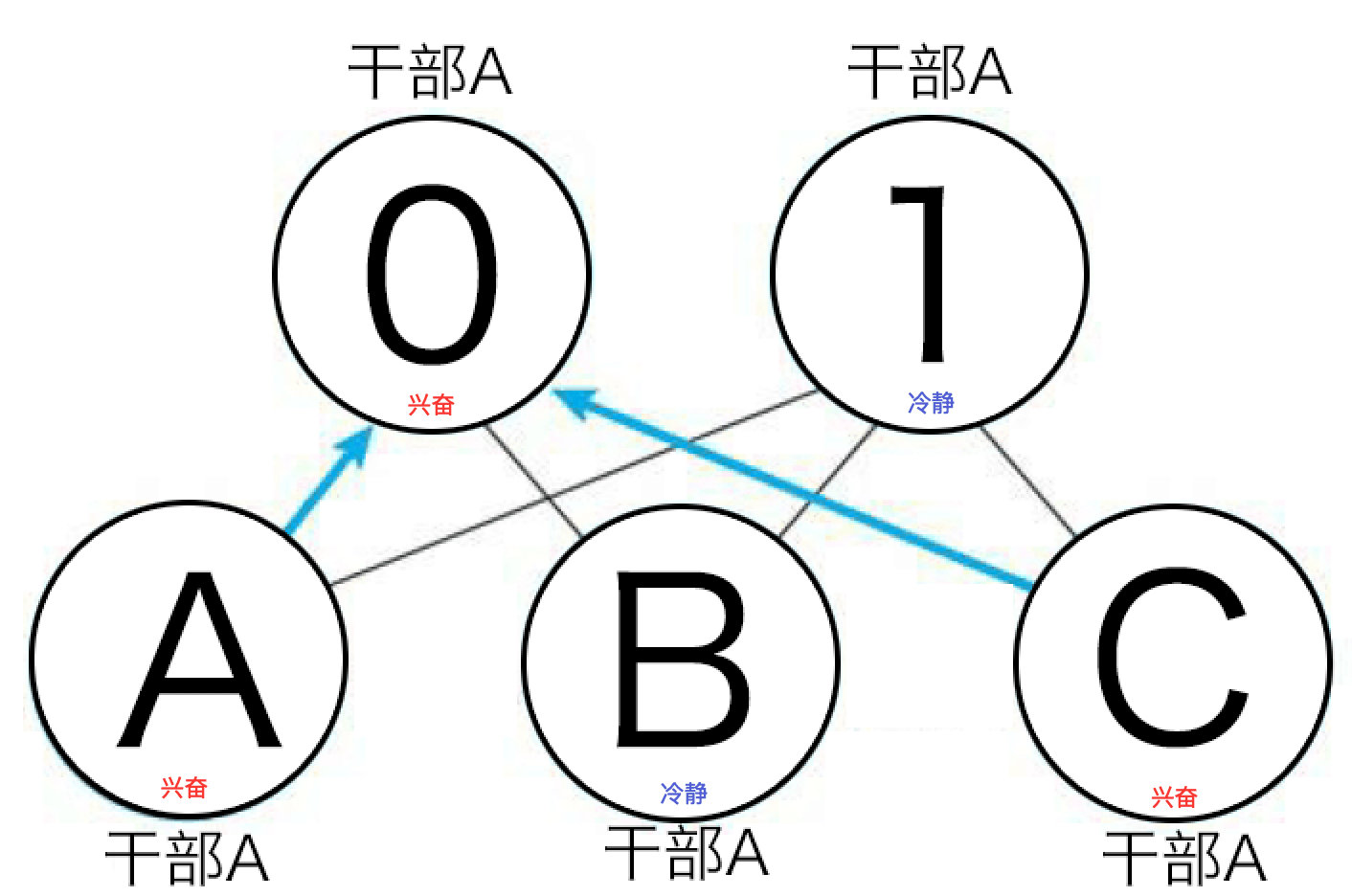
兴奋的小弟4和7向干部A传递消息,兴奋的小弟6和9向干部C传递了消息,没人向干部B传递消息。
干部A和C也接到了小弟传来的信息也兴奋了起来,于是干部A和C也向上层向大哥0发送信息,而干部B由于没有掌握到信息,就没有向大哥1发送消息。
由于大哥0是兴奋地,而大哥1是冷静的,根据之前说的大哥0的兴奋度比大哥1高,所以就判断这个图片是0
3.2 偏置
在上面的示例中,下层的兴奋度会或多或少的向上层传递,但是除了干部看中小弟和大哥看中干部的关系而传送的兴奋度外,还遗漏了一些信息,这个信息就是”噪音“,如果这些噪声迷住了每个人的脑子,就会导致无法正确的传递兴奋度信息,隐藏我们需要减少噪音的功能,也就是我们所说的偏置,将偏置放在每个人(神经元)的心中,用来忽略少量的噪音,这个心中的偏置,就是各个人固有的个性。
3.3 实例解释
在上面的示例中,我们理解了神经网络识别数字的的模式识别,而我们应该看到了每个人之间的关系(就是权重)和每个人的个性(偏置)合作推导出了答案,也就是神经网络整体的判断。所以我们应该明白,我们最终从神经网络中获取的应该是关系和个性,也就是权重和偏置,也就是我们所说的模型的参数。
4 神经网络的信息说明
上面我们通过实例考察了大哥带着小弟来识别数字0、1的结构,只要将这个组织替换为神经网络,我们就可以理解神经元进模式识别的结构。
4.1 权重与偏置
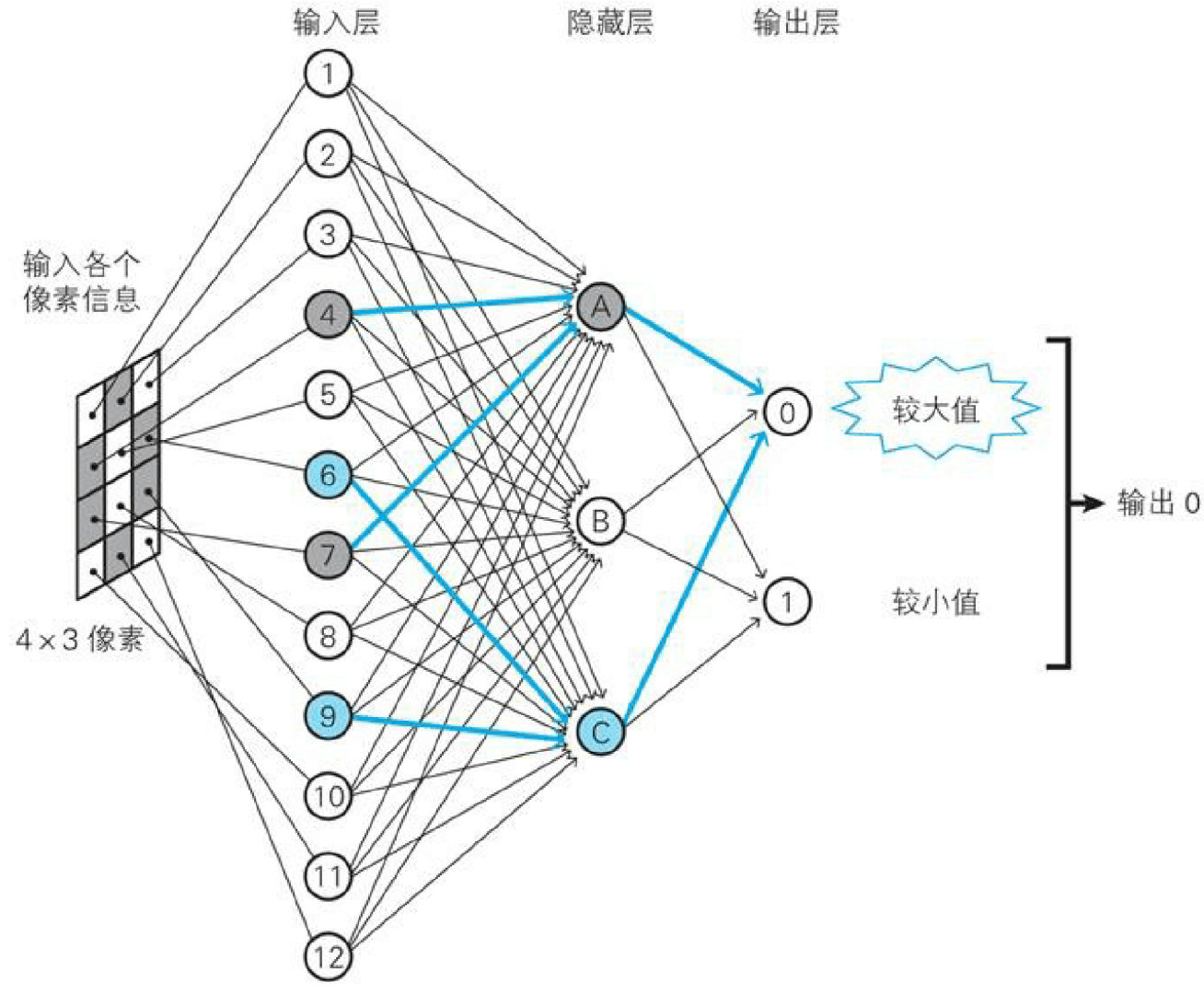
观看下面的两张图,我们就会发现,输入层的12个小弟其实就是输入层的12个神经元,隐藏层的3个干部其实就是隐藏层的3个神经元,而顶层的两个大哥就是输出层的两个神经元。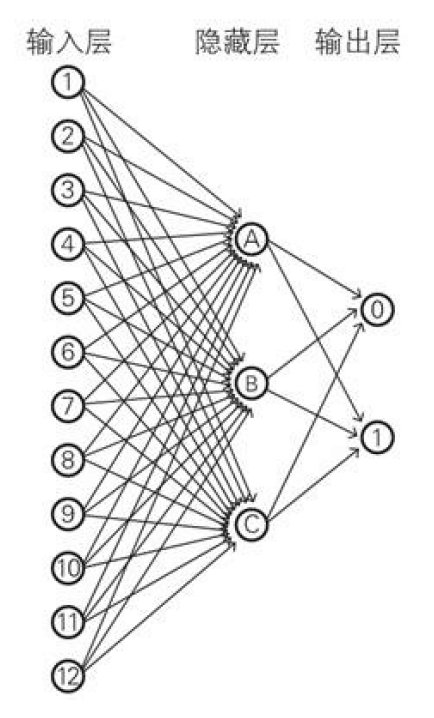
接下来,我们将层级中领导对下级的看重的关系看做神经元的权重,干部A看重小弟4和7,这种关系可以看做是输入层的神经元4和7指向隐藏层的神经元A的箭头的权重较大,隐藏层与输出层的关系类似,下面我们将这种权重关系通过图片标记出来。通过这样的权重关系,最后输出层神经元0的输出值较大,所以最终输出0
在像上图这种前一层与后一层全连接的情况下,输入图像0时,原本不希望隐藏层B神经元以及输出层1神经元也有信号传递,所以我们需要禁止掉这种信号,使信号更清晰,这种功能就是我们说的偏置。
4.2 模型合理性
上面我们将小故事翻译成了神经网络,但是也不能保证一定能求出权重和偏置。如果想实际建立基于上面这个想法的神经网络,能充分解释所给的数据就能验证它的合理性,这点需要一定的数学计算,需要将我们的语言描述转化为数据的式子,我们会在下篇文章开始讲一些会用到的数学。
4.3 网络自学习的神经网络
本文开篇我们说神经网络是通过大量计算来算出权重和偏置等参数,而在上一个示例中,我们事先假定了权重的大小(假定中层对小弟的看看着关系),那么这个权重的大小应该如何确定呢?神经网络中比较重要的一点就是利用网络自学习算法来确定权重大小
神经网络的参数确定方法分为有监督学习和无监督学习,在这个系列里我们只介绍有监督学习。
4.3.1 有监督学习
有监督学习:为了确定神经网络的权重和偏置,事先给予数据,这些数据成为学习数据、训练数据。根据给定的数据确定权重和偏置,称为学习、训练。
4.3.2 最优解
神经网络是如何学习的呢?
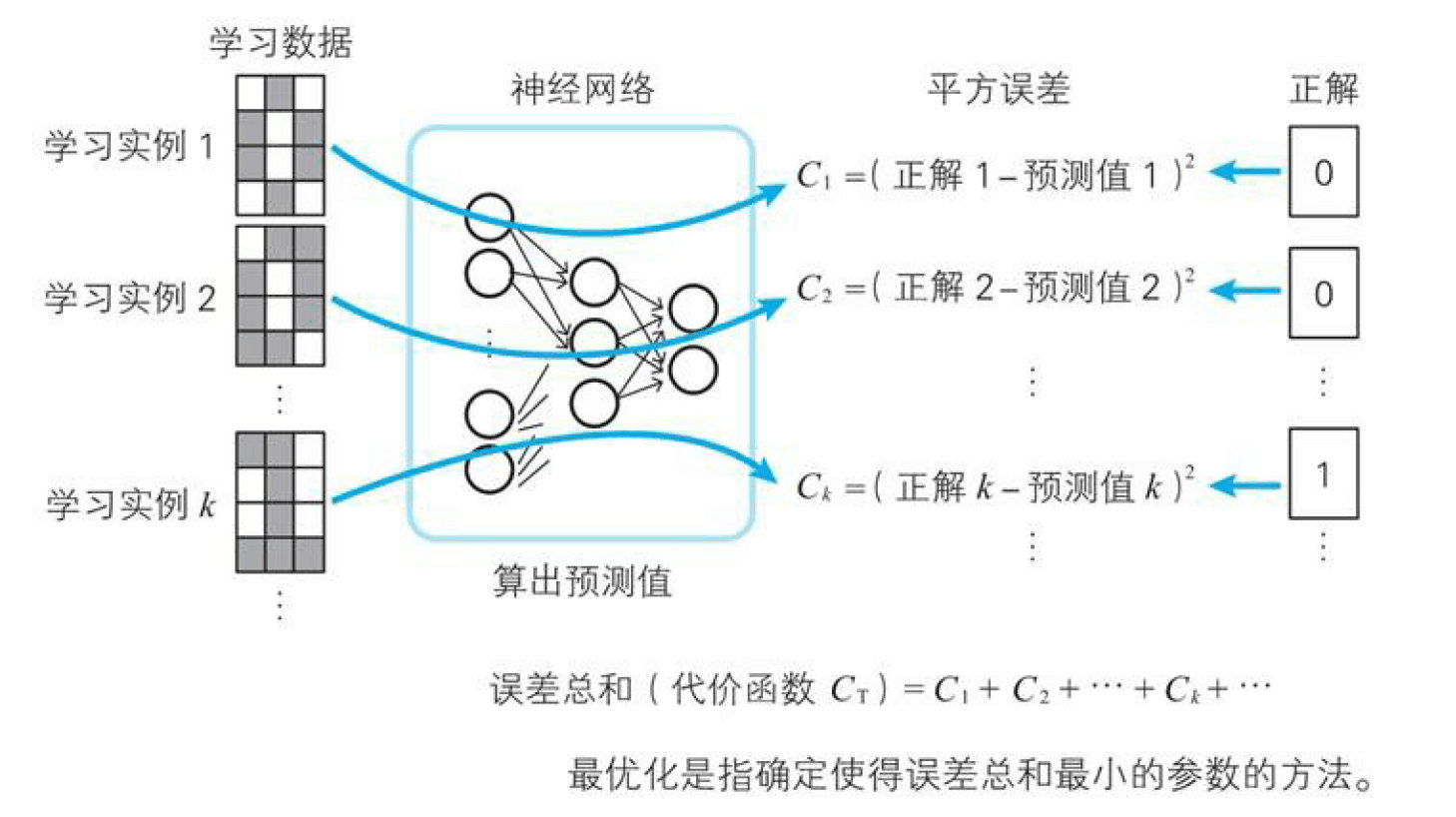
神经网络学习的思路:计算神经网络得出的预测值与正解的误差,确定使误差总和达到最小的权重和偏置,这在数学上成为模型的最优化4.3.3 代价函数
关于预测值和正解的误差总和,有各种各样的定义。这个误差的总和称为代价函数,符号表示是${C}_{T}$(T是Total的首字母)
我们这个系列中使用最经典的方式平方误差和,利用平方误差确定参数的方法在数学上成为最小二乘法,它在统计学中是回归分析的常规手段。
平方误差和:通过计算预测值与正解的误差的平方再求和
下一篇开始,我们就要正式的进入数学的领域,兴奋不兴奋!
评论请转至原文链接
本文来自纳兰小筑,本文不予回复,评论请追溯原文