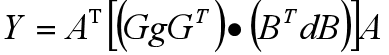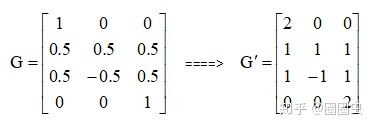本文是基于ARM平台的CNN加速算法Winograd的量化原理及实现过程。
作者:圈圈虫
首发知乎
背景
2019年已经过半,今年人工智能-计算机视觉方向在边缘计算、移动终端、嵌入式终端的产品落地进入白热化阶段。终端落地的很大一个指标依旧是Inference Time,网络模型压缩的需求越来越大,其中网络模型量化(低比特量化)开始大规模在终端设备上部署并取得了较好的市场认可,同时上游芯片设计公司依次推出了针对低比特量化(Int8)的专属加速指令集或Int8-Tensor-Unit。
然而实际操作中有一个很现实的问题,那就是当前网络模型大量使用的Conv3x3s1在Float32推理过程中采用了Winograd算法(理论上论文中最快的F(6,3)加速比是5.0625,实际工程中即使引入更多的访存、矩阵转换耗时后的最优加速比也有3.0左右),极大减少计算量,而反观目前int8的推理过程,绝大多数基于Im2col+SGEMM或Direct Conv的计算方式进行量化。最终导致大量使用Conv3x3s1结构的网络模型采用Int8量化后的速度相比Float32没有可见优势,甚至更慢。
“魔高一尺道高一丈”,Int8 Winograd被推上舞台,开始它的表演。
量化原理
本文尽量从工程角度来介绍Int8 Winograd F(2x2,3x3)的实现细节,至于Winograd的原理不想讲。(可以看看这篇详解Winograd变换矩阵生成原理
Winograd的计算公式
Winograd F(2x2,3x3),到底在计算神马?里面的“2x2”和“3x3”是啥意思啊!
- “2x2”: 输出4个结果(因为2x2 = 4)
- “3x3”: 卷积核是3x3(conv3x3s1的卷积核当然是3x3)
因此,需要输入的Feature Map就是4x4的matrix。我们回到上面那个Winograd公式中:
- Y 输出的matrix[2,2],4个结果
- g 卷积核matrix[3,3],9个数据
- d 输入的matrix[4,4],16个输入
A^T ,G,B^T都是已知的matrix:
Winograd计算转换所需的辅助Matrix
好,Winograd计算过程介绍完了!后面有空补充一份python实现。
目前我能够掌握的Convolution Int8量化的公式是下面这样的:
实现过程
初看这两个公式,这怎么可能融合到一起嘛!
远看炮台吓死人,近看五对负重轮
回顾下我们的目标是Winograd定点化计算。我们并不需要对Winograd的计算过程进行量化,而是将量化后的数据进行Winograd计算。(应该不是一个意思吧)
再看看那个唬人的Winograd公式,除了Matrix G中有0.5,其他的Matrix都是Int8的整形数据了。那么只需要做一个简单的操作将Matrix G变成Int8整形就行了:G’ = G x 2
想办法将其变成整形数据
最后我们得到的Y’再除以4(为什么是4不是2呢?因为乘以了两次的,G与G^T)就是我们需要的Y了。我们的Int8 Convolution 计算流程变化如下:
Int8 Convolution 流程:
input_fp32 -> quantize -> int8-conv -> Int32 -> dequantize -> output_fp32
Int8 Winograd流程:
input_fp32 -> quantize -> int8-winograd -> Int32 -> dequantize -> output_fp32
至此Int8 Winograd F(2x2,3x3)核心计算过程就讲好了。
精度讨论
这里介绍的Int8 winograd F(2x2,3x3)的精度与普通Int8 Convolution完全一致!最终网络模型的精度呢?这个与大家Int8的量化策略有关了,这个得单独挖坑详细讨论,什么post train quantization、quantize aware train之类的吧。
推广应用
Int8 Winograd F(4x4,3x3)同理可得。目前腾讯CSIG优图实验室开源的ncnn推理框架在年初已经开源支持Int8 Winograd的两种实现,欢迎试用。
最新进展
ncnn Int8最新优化进展:已完成更低位宽的a7w6(activation 7bit,weight 6bit)量化实现及arm32/arm64平台优化。
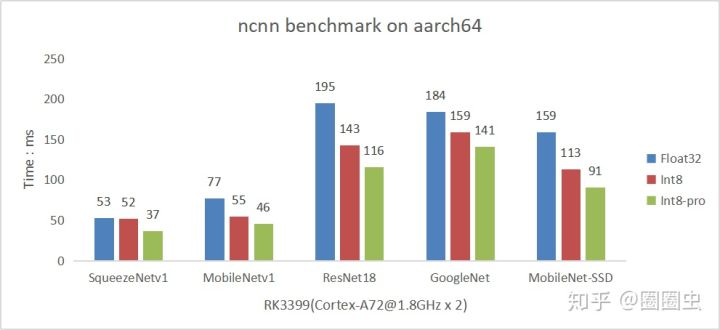
The benchmark of ncnn Int8 20190603
更多AI移动端优化相关技术干货请关注嵌入式AI专栏 及知乎账号圈圈虫