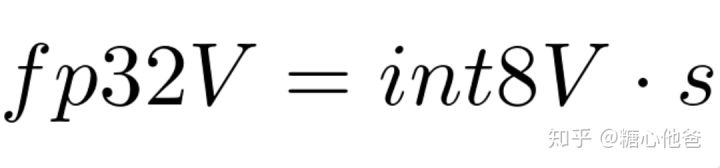最近调研了一些关于CNN网络量化的论文,结合之前基于MNN的使用感受,打算跟大家谈一谈MNN中的模型量化以及其相关的数学模型。本文可能关于数学的描述会更多一些,后面会再出一些偏工程的描述文章,方便大家对比。MNN中提供了一个功能强大的工具箱,其中有一个工具在生产环境中应用非常广泛(特别是低算力场景)---- 那就是模型量化工具。与此同时,MNN中也相应的集成了与量化工具配对使用的量化算子,目前支持对二元运算、conv、dwconv算子的量化支持。
首发:https://zhuanlan.zhihu.com/p/81243626
作者:张新栋
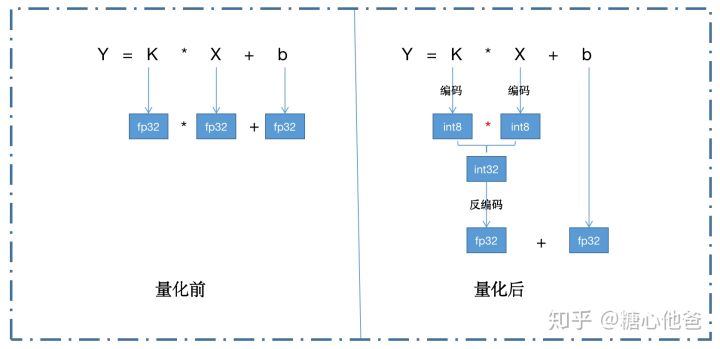
使用模型量化的好处,笼统来说,就是将fp32的计算转化成int8运算,从而达到模型压缩、算子加速的目的。我们可以对比一下卷积算子量化前后两者的数据流:
从上面数据流我们可以看到,通过量化操作后,我们将conv2d-fp32的操作,转化成了如下几个操作的组合:权重编码、fp32-to-int8-IO、输入编码、fp32-int8-IO、conv2d-int8操作、输出反编码、int32-to-fp32-IO。假设当前计算的寄存器位宽为128,理论上fp32算子的峰值加速比为4,int8算子的峰值加速比为16。但为什么我们量化后,从fp32到int8的加速比达不到4呢?因为我们还做了很多额外的操作,IO上的操作如两个fp32-to-int8-IO、一个int32-to-fp32-IO,编码操作如一个权重编码和一个输入编码,反编码操作int32-to-fp32-IO。在经过这一系列额外的操作后,很多情况下,我们依然还能达到约1.2~1.5的加速比。与此同时,量化还能减轻模型的存储压力和内存压力(fp32的权值转由int8权值进行存储)。缺点嘛,会带来精度损失!如何最小化精度损失呢?
量化的模型建立
现在我们知道了如何做量化推断,下一步是如何去建立量化模型,或者说我们应该用一个什么样的方式才能求得量化权重和量化输入呢?现在已知我们的输入为fp32,我们想用int8来对原fp32的数据进行表示,其中的转化关系假设为:
fp32和int8值之间的转化关系
对于每个数据块,我们都希望用一个尺度因子来对其进行int8的刻画,这个尺度因子就是上面式子中的s。经过上面式子之后,我们就能找到int8值和fp32值的一个对应关系。下面我们看看具体的从fp32到int8的值求解过程,这里假设我们已经知道了尺度因子s和阶段关系,那么int8的值我们可以通过如下式子获得:
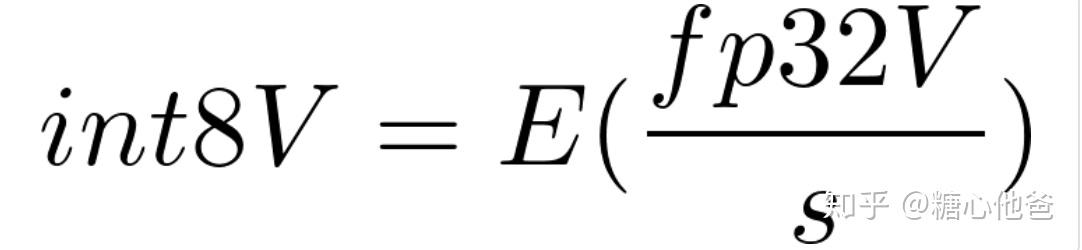
int8值的求解过程
其中E是一个分段函数,表示如下。在数轴上看这个函数,是一个分段线性函数,且每个分段的导数为0,在阶梯跳跃处的整数点不可导。这个性质是一个很好用的性质,文中后续将会用到这个性质。
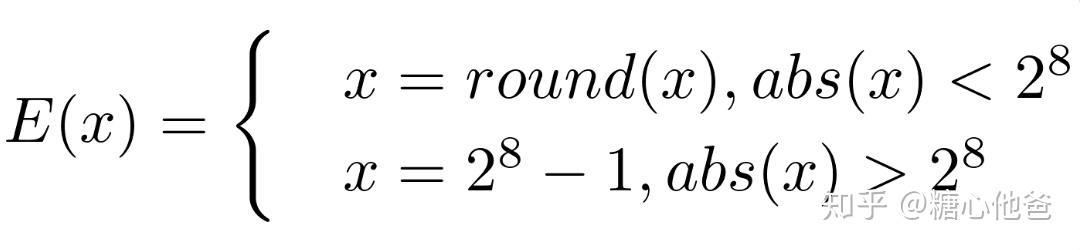
截断函数
在经过了这一系列过程后,我们就由fp32值得到了int8的值,我们进一步抽象这个过程,为了后面的数学推导做准备。为此,我们再定义一个函数f,我们称之为编码函数;反过来f的逆,我们称之为反编码函数,由上式我们很容易得到:
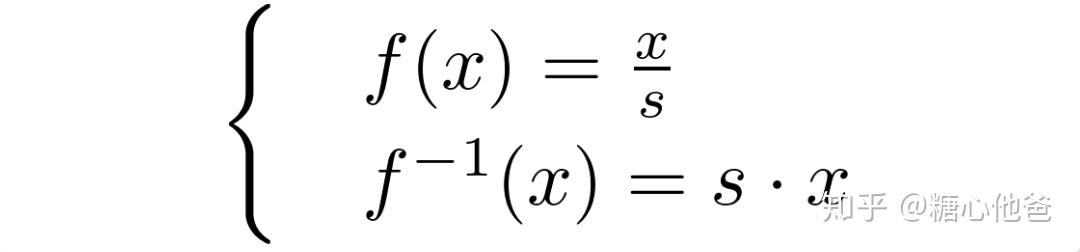
所以,在进行int8值的量化编码时候,我们执行了如下操作,
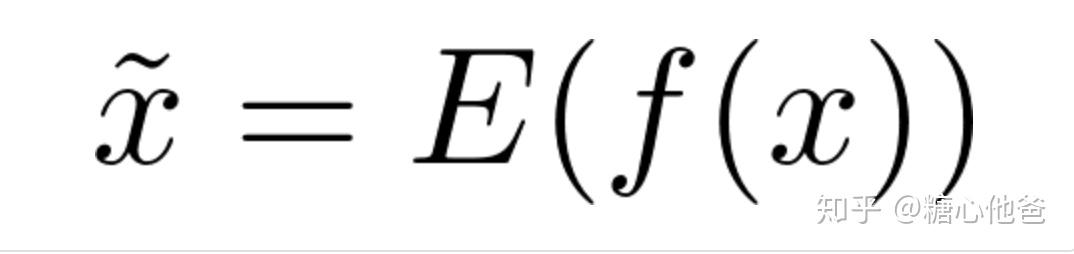
int8的编码过程
由于进行了数据截断,该过程不可逆,所以这个是一个信息损失的过程,为了度量损失的程度,我们下面将会介绍两种思路,也是MNN中解决该问题的两种算法。其目的都是为了,尽量的在编码过程中减少信息的损失。一种是从概率分布的角度出发的,目的是让编码后的数据分布和编码前的数据分布尽可能的一致,采用的概率分布度量为KL-散度;另一种是从最优化优化角度出发的,目的是让编码后的数据在进行反编码后的结果,尽可能和原数据接近,采用的度量可以是L2、L1或是广义范数,但由于L2度量的优化算法求解方便,我们后面也主要基于L2度量进行讨论。
从概率出发的求解思路(对应MNN中的KL求解)
假设我们这个需要进行量化的算子为conv2d算子,数学表达式为y = k*x + b,我们需要对该层的输入特征x和权重k同时进行量化。我们可以借助的数据,可以是训练数据中抽取的一批样本,也可以是测试数据,一般选取1000左右的数据就可以达到很好的效果,当然选取的数据越多、理论上逼近效果越好,但缺点是求解时间就会相应的增加。从概率的角度出发,我们知道,需要去度量编码后的int8数据和原始fp32数据的分布差异,度量我们可选用KL-散度。但是目前我们还不知道尺度因子是什么,我们该如何去计算尺度因子呢?确定尺度因子的方式也很简单,只要确定采样方式就可以。TensorRT的量化算法,这个PPT中介绍了一种采样方式,思路比较偏工程师思维,简单、暴力、好用!具体的求解过程,大家可以参考PPT,数学上已经没有什么好讨论的了,后面我们也会再写一篇文章从工程上介绍该方法的实现过程。得到了量化后的数据,假设为其分布为Q,量化前的分布为P,由于两者的采样粒度可能不一样。如PPT中介绍的,原数数据的采样粒度为2048,量化数据的采样粒度为128,所以两者不能直接求KL散度。解决的方式也很简单,只需要对粗粒度的信号进行上采样就可以,即对Q的分布进行一个上采样,如由128上采样到2048。假设分布Q经过上采样后得到Qe,我们就可以计算Qe和P的KL-散度。最后尺度因子的确定也很暴力,枚举所有采样,选取KL-散度最小的采样所对应的尺度因子即可。KL散度的计算方式如下,
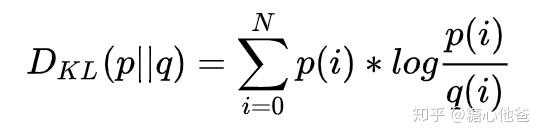
从优化的角度出发(对应MNN中的ADMM求解)
从优化的角度出发,又该如何进行建模和求解呢?首先如果我们想从优化角度去解决该问题,我们首先需要先建立目标函数,这里我们定义一个目标:希望编码后的数据(int8)经过反编码后,跟原数据的”距离“尽可能的接近。该描述可以通过如下数学公式进行刻画:
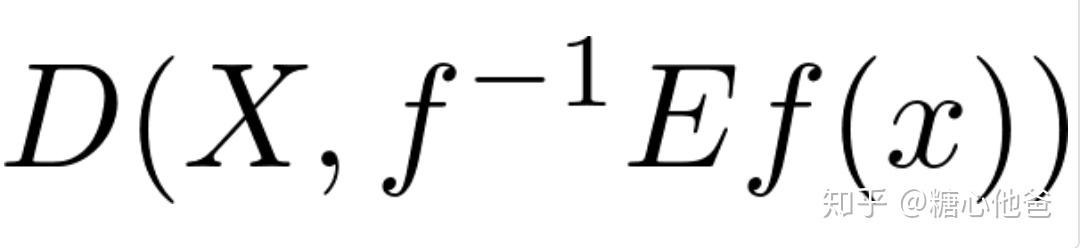
广义目标函数
进一步的,假设我们这里选定的度量D为L2度量,f和E的选取跟文章一开始时候介绍的一致,我们可以将上面式子转化如下:

目标函数
所以,求解尺度因子s的过程,就变成了极小化上述目标函数的过程。而且,上面我们也提到过,E的函数性质很有特点,其在阶段域内整点处处不可导,其余点处处导数为0。利用该阶段函数的特点,我们很容对上述目标函数进行求解。不过先别急,我们先算算上面目标函数相对于s的导数,如下:
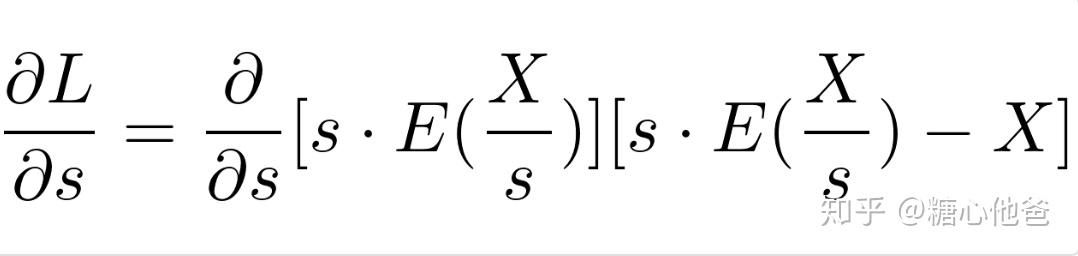
目标函数L关于s的导数
由于E函数的特点,我们知道E关于s的隐函数求导,在可导处的函数值处处为0,不可导的地方我们先忽略掉(工程实现只需要避免奇点即可)。我们可以将上述式子再进一步简化如下:
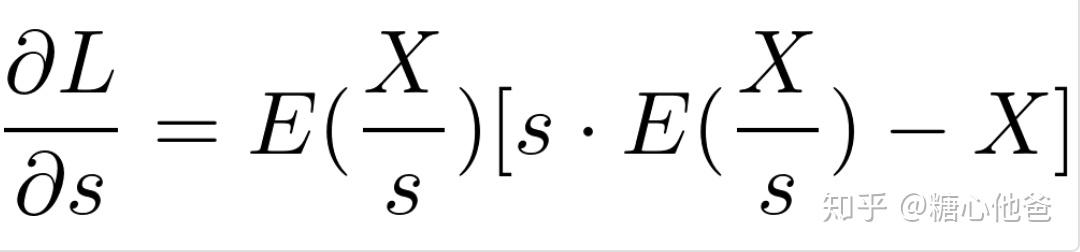
目标函数L关于s的导数
再得到目标函数关于s的导数公式以后,后续的求解就非常简单了,我们给出几种求解思路。第一种,比较直接的方法,可以采用梯度下降法,流程简单如下:
## 给定s的初值(可以统计数据的min、max进行强映射初始化)
1、 计算L关于s的梯度
2、 更新s的值
3、 判断终止条件
4、 更新步长第二种,稍微麻烦点,由第一种算法我们可以知道,步长的选取是启发性的,收敛性虽然基本都能 得到保证,但如果我们想自适应的计算最优步长,可以采用golden-search的求解方式,求解过程跟梯度下降法很接近,如下:
## 给定s的初值(可以统计数据的min、max进行强映射初始化)
1、 计算L关于s的梯度
2、 计算最优步长
3、 更新s的值
4、 判断终止条件第三种方式,类似一阶收敛(梯度下降、golden-search)和二阶收敛(牛顿等)我就不再拓展了;我们这里介绍一下MNN中采用的优化算法,ADMM(交替方向法)。在得到L关于s的梯度公式后,如下图:
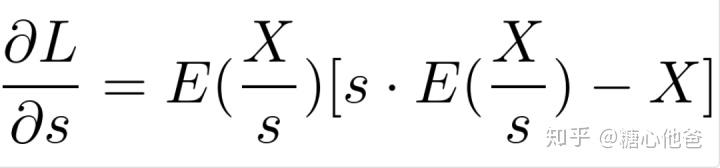
目标函数L关于s的导数
其进行了一个概念转化,求解L的极小化问题,转化成求解L关于s的导数为0的数学问题。但由于函数E中还包含了未知数s,MNN在求解这个数据问题的时候,采用了ADMM的思想,先freezeE中的s变量,进行s值的求解;然后再通过求解后的s去估计E的值,如此反复直到s值收敛到最优。于是上述的式子要弱化为如下公式:
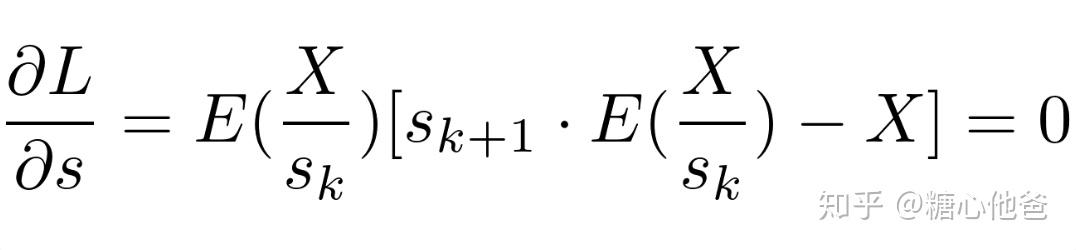
ADMM等式构造
所以迭代的过程就变成了交替迭代求解如下两个公式的过程,
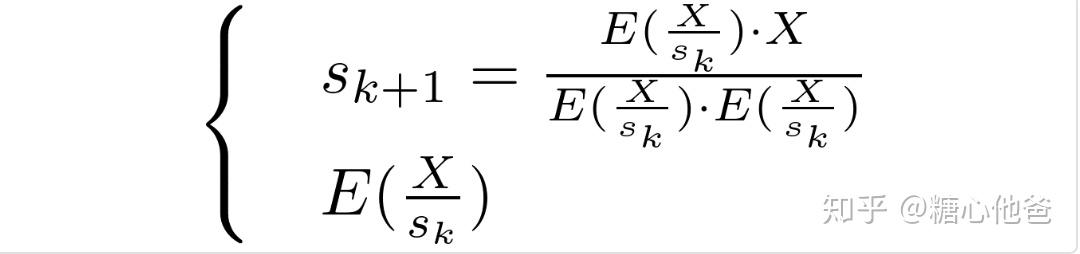
ADMM的迭代过程
于是算法流程可构造如下:
## 给定s的初值(可以统计数据的min、max进行强映射初始化)
1、 计算E的值
2、 更新s的值
3、 判断终止条件关于三种算法的终止条件判断,可以采用l2 loss的方式即||L(k+1) - L(L(k)) || / N。也可以采用相对变化率的方式,即当前迭代变化和上次迭代变化的比值。不过其实不判断问题也不大,如MNN中的源码实现中是按照最大固定迭代次数来实现的。
最后
关于量化模型的问题定义和算法,可改进的地方还有很多,后面有机会还会继续跟大家分享。今天介绍的东西,可能数学的东西多了一点,后面我们会从工程的角度来跟大家谈谈网络量化的实现方式。欢迎大家留言讨论,关注专栏、公众号!谢谢大家!
参考
1.http://on-demand.gputechconf.com/gtc/2017/presentation/s7310-8-bit-inference-with-tensorrt.pdf
2.https://zhuanlan.zhihu.com/p/73207495
推荐阅读
专注嵌入式端的AI算法实现,欢迎关注作者微信公众号和知乎嵌入式AI算法实现专栏。
更多嵌入式AI相关的技术文章请关注极术嵌入式AI专栏。