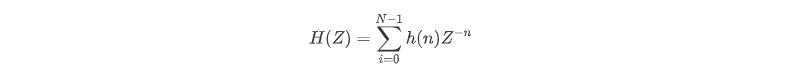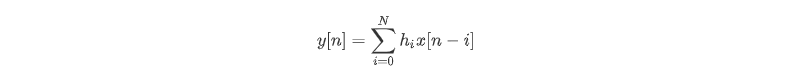FIR滤波器之What？

LTI线性时不变系统冲激响应按照其是有限长还是无限长可分为FIR(Finite Impulse Response)有限长冲激响应系统以及无限长冲激响应IIR(Infinite Impulse Response)系统。FIR是全零点系统，也即Z传递函数在Z复平面极点全在Z=0处。至于这些概念是如何得来的，不是本文重点，如果有兴趣深究，可以查阅数字信号处理方面的书籍。

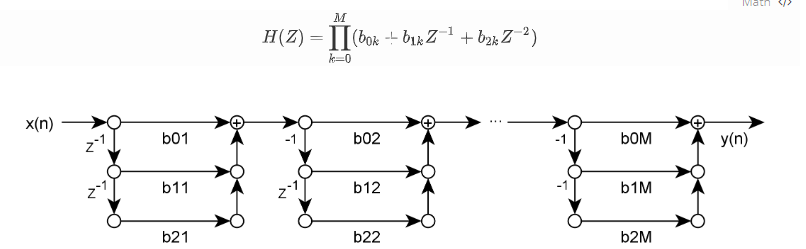
FIR滤波器具有多种实现形式，比如直接型、二阶级联型、Lattice结构，都只是上述基本传递函数的不同数学表达形式，没有本质区别，只是在具体算法实现上各具特点。这里将二阶级联形式描述如下。

二阶级联的意思是将上述传递函数分解为二阶多项式块连乘的形式，其数学表达如下：

FIR滤波器之Why？

为啥称前面的传递函数形式的系统为有限长冲激响应呢？要从概念上理解，首先须从冲激响应说起，什么是系统的冲激响应？系统在单位冲激函数激励下引起的零状态响应被称之为该系统的“冲激响应”。

那么什么又是是冲激函数呢？

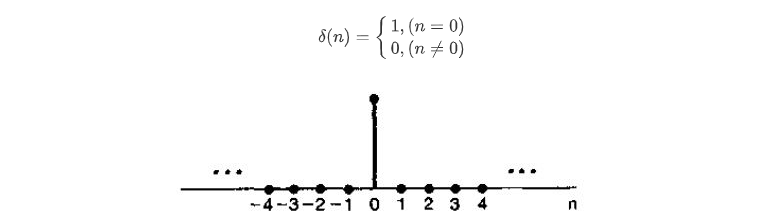
单位冲激函数（Unit-Impulse Function）是信号与系统学科中的一个重要概念。它是一个面积等于1的理想化了的窄脉冲。也就是说，这个脉冲的幅度等于它的宽度的倒数。当这个脉冲的宽度愈来愈小时，它的幅度就愈来愈大。当它的宽度按照数学上极限法则趋近于零时，那么它的幅度就趋近于无限大，这样的一个脉冲就是“单位冲激函数”。在实际工程中，像“单位冲激函数”这样的信号是不存在的，至多也就是近似而已。在理论上定义这样一个函数，完全是为了分析研究方便的需要。<百度百科>

单位冲激函数又称为狄拉克函数，定义为：

这玩意纯数学表达仅为从严谨角度出发，却不易懂，在数字信号处理领域或者称为离散系统领域，定义单位冲激（也有的称为单位采样/单位函数/单位脉冲，管它张三、李四）这里只需要明白其物理含义即可：

那么所谓单位冲激函数响应，就是一个系统输入这样一个能量激励，在输出端所观测到的响应信号，那么对于FIR系统而言，其响应在经过有限长的序列后，最后将稳定在0，这就是有限长冲激响应的内涵，而无限长则是有这样一个冲激激励后，其响应经过无限长序列后仍不会稳定到0。再进一步思考，为什么呢？因为FIR系统输出不会反馈回输入端，则保证其输出响应是有限长序列，因此，“有限冲激响应”几乎与“无反馈”等价。但是，如果采用反馈，但脉冲响应是有限的，则滤波器仍然是FIR。一个示例是移动平均滤波器，其中每次有新采样进入时都会减去（反馈）第N个先前的采样。即使使用反馈，该滤波器也具有有限的脉冲响应：在N个采样样本之后，输出将始终为零。IIR滤波器使用反馈，因此，当输入脉冲时，理论上输出会无限地振荡。所以对于这两个概念的区分从字面去理解即可。

在实践中，即使是IIR系统，其脉冲响应也通常接近零，并且可以忽略不计。但是，引起IIR或FIR响应的物理系统是不同的，这就是区别的重要性。例如，由电阻器，电容器和/或电感器（也许还有线性放大器）组成的模拟电子滤波器通常是IIR滤波器。另一方面，基于不使用反馈的抽头延迟线的离散时间滤波器（通常是数字滤波器）必然是FIR滤波器。模拟滤波器中的电容器（或电感器）具有“记忆特性也即储能特性”，并且其内部状态不会因脉冲而完全放松。但是在后一种情况下，在脉冲到达抽头延迟线的末端之后，系统不再对该脉冲进行存储，并返回到其初始状态。超出该点的脉冲响应恰好为零。多说一句，在使用IIR时，是否稳定包括在模拟电路设计时，需要考虑的一个重要指标就是其系统的相位裕度的概念。有兴趣的可以去研究一下。

FIR滤波器之Where？

FIR滤波器的应用领域非常的广泛：

音频信号处理领域，会在信号处理层大量运用FIR滤波器进行信号滤波
Sigma-Delta ADC芯片内部就利用数字逻辑电路实现了FIR滤波器
涉及到采集信号的仪器仪表领域广为应用
系统辨识领域，对于系统建模也常常采用滤波器滤除采集信号，以消除噪声提高建模的准确性
图像处理领域也广为应用
......

说了这么多，就是想说这个东东非常有用，个人认为这是电子类开发工程师进阶神器，值得深入研究，反复探究，这也是为什么花这么多精力写这个系列的初心，希望自己的一些经验你能帮助到其他的人。所以如果你没有这方面的经验，刚好看到这系列的文章，还请帮忙转发分享以帮助到更多的人，哈哈哈。当然如果您是这方面的行家里手如果发现文中有错误或者需要改进的地方，也真诚的期待能告诉与我，帮助我纠正错误。所以导读中所说恳请指正，绝非套话。

FIR滤波器之When？

当实现传感器时，个人建议首先理清楚信号链模型，信号的频域带宽，是否有潜在混入噪声的可能。是故个人认为：

如果在硬件电路处理后任然有噪声，此时就可以考虑采用滤波器，如果所用芯片算力不错，就可以考虑采用FIR滤波器
如果在硬件也能实现有源滤波器能解决产品中的噪声干扰，但是发现硬件的方法需要成本比较高，或者PCB面积受限时，也推荐考虑采用数字滤波器实现。因为往往有源滤波器要实现一个比较好的通频带高Q值时，其阶数往往很高，而且可能需要一些特殊规格的电阻电容实现所需的频带，此时数字滤波器仅需要一段代码搞定，而且效果往往比硬件滤波器更好也更灵活。
如果在系统中发现采用IIR拓扑类型滤波器无法满足线性相位需求，或者发现使用IIR滤波器，滤波器输出出现严重失真或者不稳定现象时，推荐考虑采用FIR滤波器。
再比如你是用FPGA设计一个系统，也需要实现模拟信号采集，此时也可以考虑直接用数字电路直接实现FIR滤波器，因为FPGA的硬并行特性为实现高阶FIR滤波器提供了非常好硬件基础。
......

FIR滤波器之How？

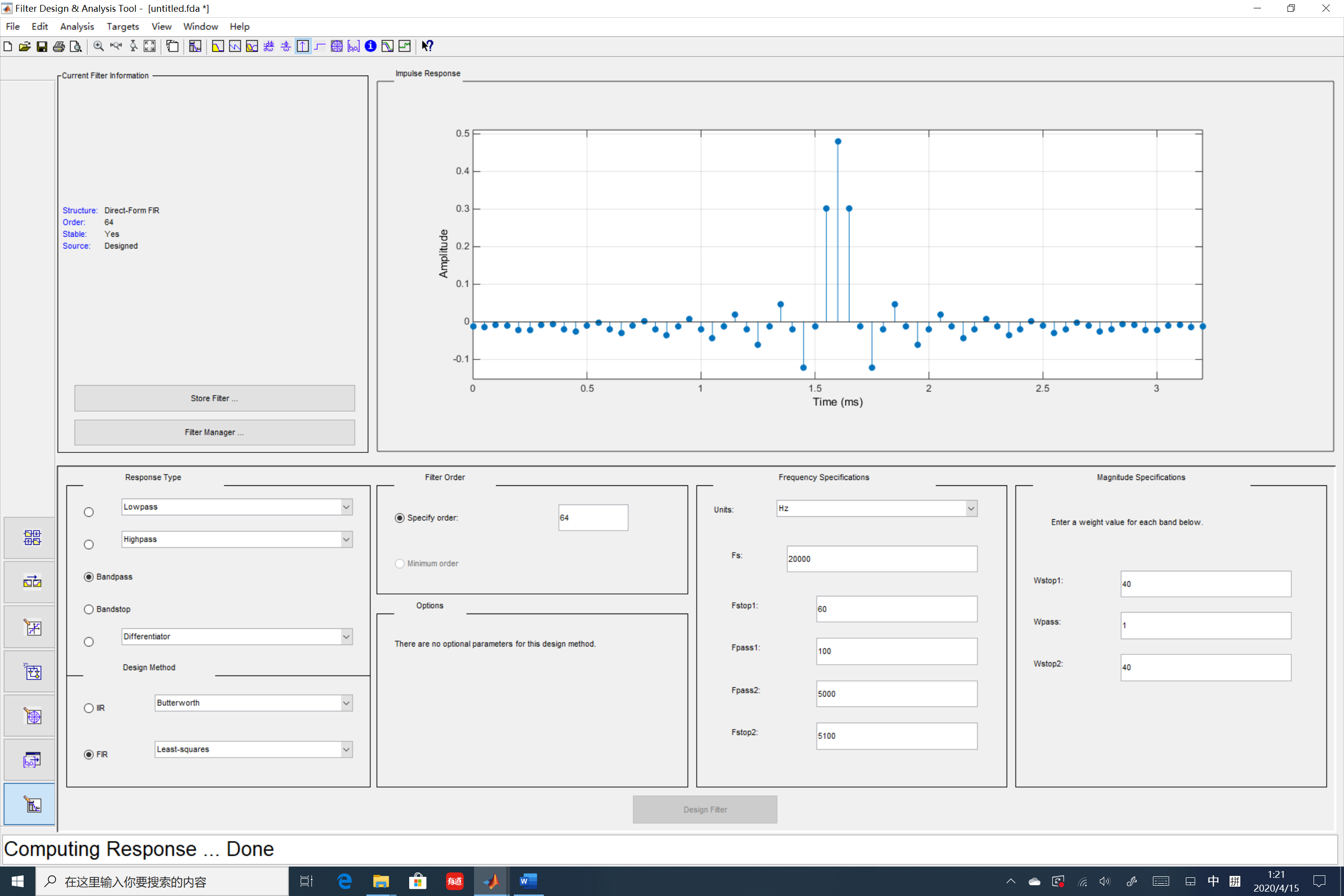
设计FIR滤波器从书本知识，可以发现有窗函数法、切比雪夫逼近法、最小均方差等方法，这些方法从数学理论上给出了设计原理，但作为工程师而言，个人认为只需要理解其概念内涵即可。学以致用才是目的，所以强大的MATLAB 工具fdatool以及实现了这些基本的设计方法。当然如果对于MATLAB函数很熟悉，直接来段MATLAB程序效果也是一样的。这里仍然利用fdatool来示例如何设计实现FIR滤波器。

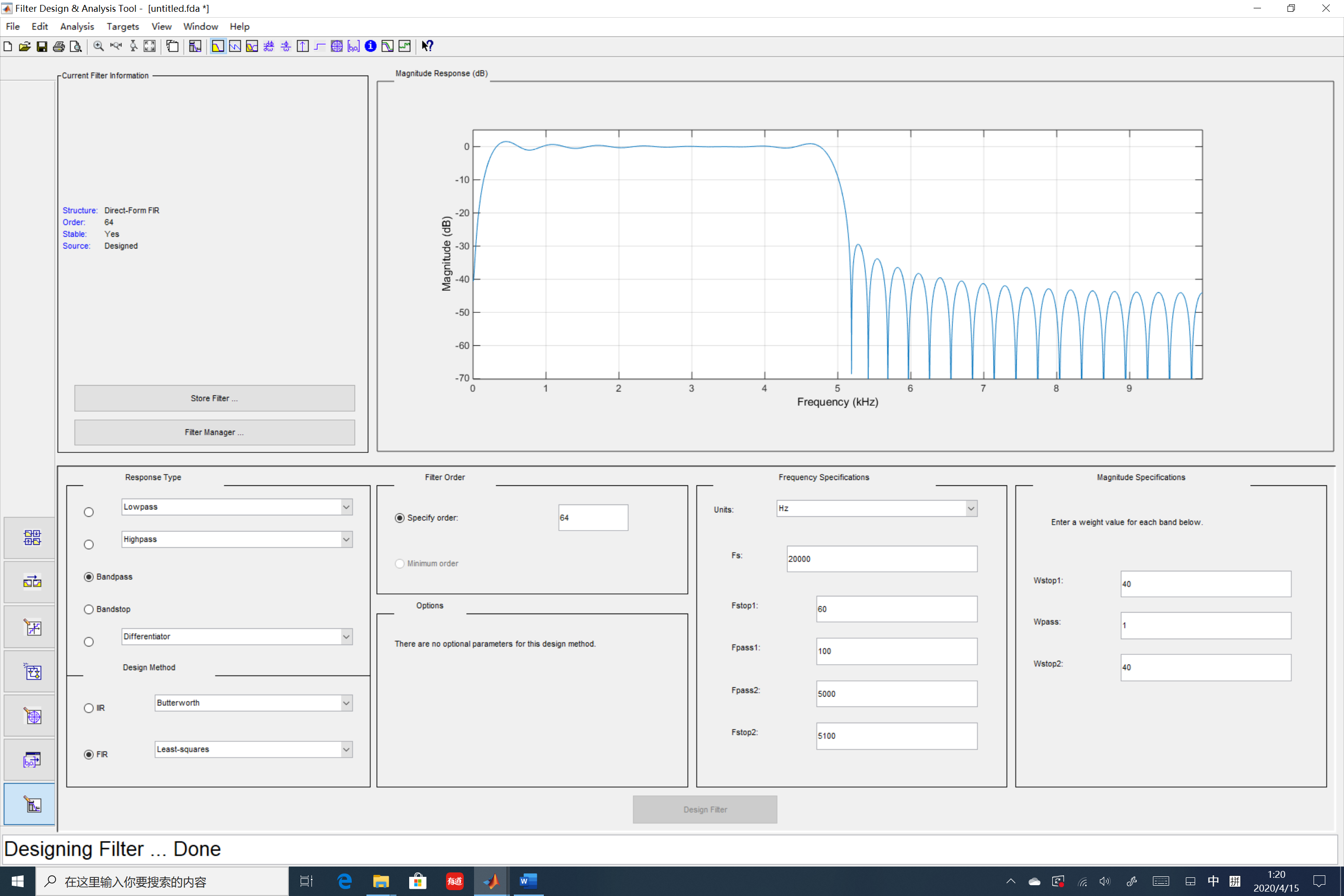
本文以实现采样频率48kHz，带宽为100Hz～10KHz带通滤波器，假定是一个麦克风语音采集系统，人的发声频率在100Hz(男低音)到10000Hz(女高音)范围内。

假设设计一个512阶的FIR带通滤波器，其指标为：

Fstop1为60Hz, Fpass1为100Hz
Fpass2为10000Hz, Fstop2为10200Hz
Wstop1 为40dB,Wstop2 为40dB,

其幅频响应为：

相频响应如下图，可见在通频带内，随频率的增加，其相位延迟也是线性增加的，这就是线性相位的含义。

前面说到冲激响应，这里将图附上帮助理解。

其参数太长就不贴在这里了，直接放到测试代码中。

接下来就进行C代码实现，由其Z传递函数，比较容易得到其差分方程为：

C语言实现及测试程序如下：

#include <stdio.h>
#include <math.h>
#include <string.h>

/*长度应为阶数+1*/
#define FIR_RANK  64
typedef float E_SAMPLE;
typedef float E_COEFF;

/*定义移动平均寄存器历史状态*/
typedef struct _t_FIR_STATE
{
    E_SAMPLE x[FIR_RANK];
    int index;
}t_FIR_STATE;
typedef struct _t_FIR_COFF
{
    E_COEFF coeff[FIR_RANK+1];
}t_FIR_COFF;

void fir_init(t_FIR_STATE * pFir)
{
    memset(pFir,0,sizeof(t_FIR_STATE));
    pFir->index = -1;
}

E_SAMPLE fir_filter(t_FIR_STATE * pFir,const t_FIR_COFF *pCff,E_SAMPLE xn)
{
    double yn=0;
    int i=0;
    if(pFir->index==-1)
    {
        for(i=0;i<FIR_RANK;i++)
        {
            pFir->x[i] = xn;
        }
        pFir->index = FIR_RANK-1;
    }

    //if(pCmf->index<FIR_RANK-1)
    yn = pCff->coeff[0]*xn;
    for(i=pFir->index+1;i<FIR_RANK;i++)
    {
        yn += pCff->coeff[i-pFir->index]*pFir->x[i];
    }

    for(i=0;i<=pFir->index;i++)
    {
        yn += pCff->coeff[FIR_RANK+i-pFir->index]*pFir->x[i];
    }

    /*存储yn为下次迭代准备*/
    pFir->x[pFir->index] = xn;


    if(pFir->index==0)
        pFir->index = FIR_RANK-1;
    else
        pFir->index--;

    return yn;
}

#define SAMPLE_RATE 20000.0f
#define SAMPLE_SIZE 1024
#define PI 3.415926f
const t_FIR_COFF coff={
-0.011262440038163873,-0.013943401141922421,-0.0081737662228137248,-0.0098154763556324871,
-0.02113385595071398,-0.02217110374674186, -0.0086760432252453272,-0.0053777731960091618,
-0.020684485378668873,-0.026487927162555332,-0.0099598536658154907,-0.0020760557762302574,
-0.020234665687863043,-0.030631983578413714,-0.010974822973539177, 0.0018520388094555051,
-0.019945227624679929,-0.035904990372740073,-0.011725945979530706, 0.0077957069084101244,
-0.019771168997491595,-0.044197538806107613,-0.012256200606615813, 0.018808015681099421,
-0.01967177670413162, -0.06116090480347313, -0.012595538855093001, 0.047238864700837428,
-0.019621294906038051,-0.12211186053365741,-0.012761289558492961, 0.30206303190057837,
 0.4803940881892042,   0.30206303190057837,-0.012761289558492961,-0.12211186053365741,
-0.019621294906038051, 0.047238864700837428,-0.012595538855093001,-0.06116090480347313,
-0.01967177670413162,  0.018808015681099421,-0.012256200606615813,-0.044197538806107613,
-0.019771168997491595, 0.0077957069084101244,-0.011725945979530706,-0.035904990372740073,
-0.019945227624679929, 0.0018520388094555051,-0.010974822973539177,-0.030631983578413714,
-0.020234665687863043,-0.0020760557762302574,-0.0099598536658154907,-0.026487927162555332,
-0.020684485378668873,-0.0053777731960091618,-0.0086760432252453272,-0.02217110374674186,
-0.02113385595071398, -0.0098154763556324871,-0.0081737662228137248,-0.013943401141922421,
-0.011262440038163873
};
int main()
{
    E_SAMPLE rawSin[SAMPLE_SIZE];
    E_SAMPLE outSin[SAMPLE_SIZE];

    t_FIR_STATE fir;

    FILE *pFile=fopen("./simulationSin.csv","wt+");
    if(pFile==NULL)
    {
        printf("simulationSin.csv opened failed");
        return -1;
    }

    for(int i=0;i<SAMPLE_SIZE;i++)
    {
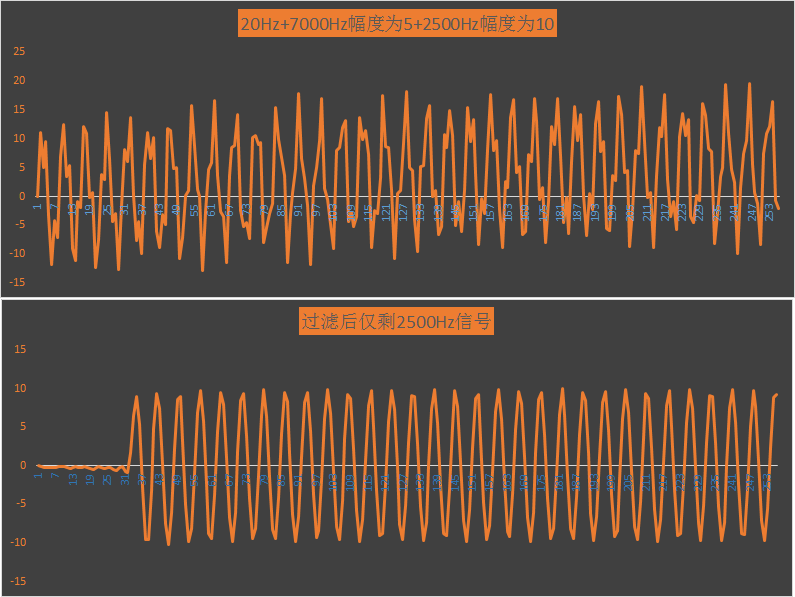
        rawSin[i]  = 5*sin(2*PI*20*i/SAMPLE_RATE);//+rand()%10;
        rawSin[i] += 5*sin(2*PI*7000*i/SAMPLE_RATE);
        rawSin[i] += 10*sin(2*PI*2500*i/SAMPLE_RATE);
    }

    /*初始化*/
    fir_init(&fir);
    /*滤波*/
    for(int i=0;i<SAMPLE_SIZE;i++)
    {
        outSin[i]=fir_filter(&fir,&coff,rawSin[i]);
    }

    for(int i=0;i<SAMPLE_SIZE;i++)
    {
        fprintf(pFile,"%f,",rawSin[i]);
    }

    fprintf(pFile,"\n");
    for(int i=0;i<SAMPLE_SIZE;i++)
    {
        fprintf(pFile,"%f,",outSin[i]);
    }

    fclose(pFile);

    return 0;
}

同样利用excel生成波形：

可见滤波效果不错。下面进行总结：

FIR滤波器与IIR滤波器相比的优势：

可以很容易地将它们设计为“线性相位”（通常是）。简而言之，线性相位滤波器会延迟输入信号，但不会使其相位失真。
很容易实现。在大多数DSP微处理器上，可以通过循环一条指令来完成FIR计算。
适合于多速率应用。所谓多速率，是指“抽取”（降低采样率），“内插”（提高采样率）或两者兼而有之。有兴趣的可进一步深入研究，无论是抽取还是插值，FIR滤波器的使用都可以省略某些计算，从而提供了重要的计算效率。相反，如果使用IIR滤波器，则即使要丢弃每个输出，每个输出也必须单独计算。
具有令人满意的数值属性。实际上，大部分DSP滤波器都必须使用有限精度算法（即有限的定点位数）来实现。由于使用了反馈，因此在IIR滤波器中使用有限精度算术会引起严重的误差问题，但是没有反馈的FIR滤波器通常可以使用更少的位来实现，并且设计人员需要解决的与非理想算术有关的实际问题也更少。
可以使用分数算法来实现。与IIR滤波器不同，始终可以使用幅度小于1.0的系数来实现FIR滤波器。（如果需要，可以在FIR滤波器的输出处调整其总增益。）使用定点DSP时，这是一个重要的考虑因素，因为它使实现更加简单。

FIR滤波器与IIR滤波器相比的劣势：

需要更多的内存和/或计算才能实现给定的滤波器响应特性。而且，某些响应对于用FIR滤波器不易实现，因为阶数太高。

另外如果使用的芯片具有乘累加指令，则非常利于实现FIR滤波器。
文章出自微信公众号：嵌入式客栈，更多内容，欢迎关注交流

手把手教系列之FIR滤波器设计

FIR滤波器之What？

FIR滤波器之Why？

FIR滤波器之Where？

FIR滤波器之When？

FIR滤波器之How？

推荐阅读

目录