文章转载于:知乎
作者:BBuf❝ [GiantPandaCV导语] 这篇文章是基于NCNN的Sgemm卷积为大家介绍Im2Col+Pack+Sgemm的原理以及算法实现,希望对算法优化感兴趣或者做深度学习模型部署的读者带来帮助。
❞
1. 前言
最近空闲时候在给MsnhNet贡献Arm端的代码,地址详见:https://github.com/msnh2012/Msnhnet 。对于卷积运算一种最常见的实现方法就是Im2Col加上Sgemm,这样可以把复杂的卷积运算转换成两个矩阵直接相乘,在OpenBlas中就提供了矩阵相乘的多种算法如Sgemm。所以这篇文章的目的就是讲清楚如何对卷积层进行Im2Col将其转换为矩阵乘法,以及为了进一步加速矩阵乘法的计算过程使用了NCNN中的Pack策略,最后再使用Neon对主要的计算过程进行优化。
2. Im2Col+Sgemm计算卷积原理
相信大家对于卷积的概念都非常熟悉了,这里就不再重复提起了,我大概说一下我了解的卷积的计算方式有哪些吧。首先是暴力计算,这是最直观也是最简单的,但是这种方式访存很差,效率很低。其次是我在基于NCNN的3x3可分离卷积再思考盒子滤波介绍过的手工展开某些特定的卷积核并且一次处理多行数据,这样做有个好处就是我们规避掉了一些在行方向进行频繁切换导致的Cache Miss增加,并且在列方向可以利用Neon进行加速。再然后就是比较通用的做法Im2Col+Sgemm,这种方式可以使得访存更好。其它常见的方法还有Winograd,FFT,Strassen等等。
本文的重点是尝试讲清楚Im2Col+Sgemm的算法原理及其实现思路,以及在Im2Col的基础上进行数据Pack进一步改善矩阵乘法的计算中由于Cache Miss带来的性能下降。
「首先」,让我们来考虑一个单通道的长宽均为的输入特征图,并且假设卷积核的大小是,那么它经过Im2Col之后会变成什么样呢?如下图所示:
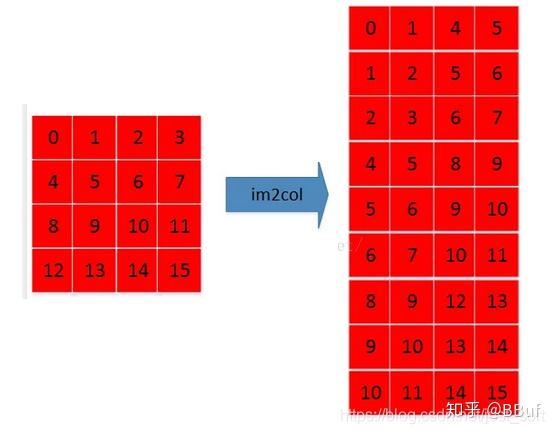
单通道长宽均为4的特征图Im2Col的结果
其实变换的方式非常简单,例如变化的第一步如下图所示:
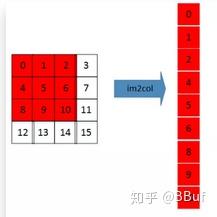
Im2Col的第一步
直接在卷积核滑动的范围内,把所有元素顺序排列成一列即可,其它位置处同理即可获得Im2Col的结果。多通道和单通道的原理一样,如下图所示:
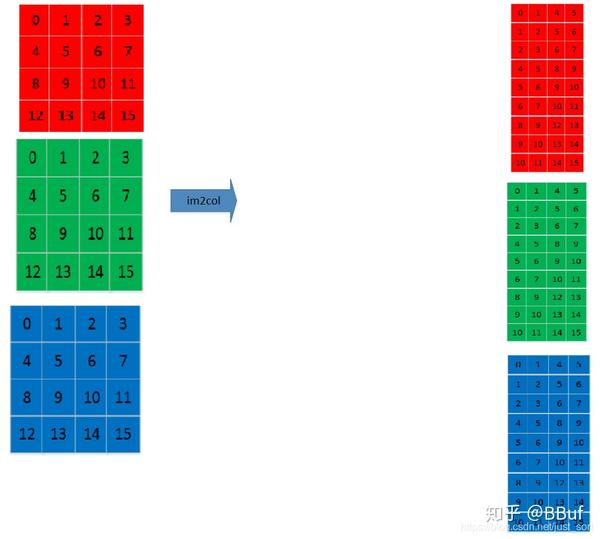
3通道特征图的Im2Col
「其次」,让我们来考虑一下卷积核经过Im2Col操作后应该是什么样子的,对于多通道如下图所示(单通道就是其中一种颜色):
卷积核的Im2Col
最后,输入特征图和卷积核都进行了Im2Col之后其实都变成了一个二维的矩阵,我们就可以使用矩阵乘法来直接计算结果了。下图展示了一个的特征图和一个的卷积核经过Im2Col之后之后使用Sgemm进行计算的过程,其中每一种颜色都代表一个输出通道。
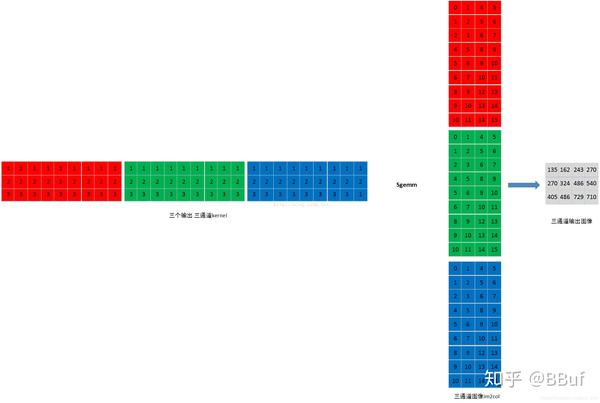
4x4x3的特征图和3x3x3的卷积核使用Im2Col+Sgemm策略进行卷积获得一个2x2x3的特征
相信看了上面几个图之后,大家对Im2Col和Sgemm结合用来做卷积的过程有所了解,为了更加严谨,下面还是以「公式化的形式」再来总结一下:
假设输入的特征图维度是,表示Batch为1,通道数为,高为,宽为,卷积核的维度是,表示输出通道数为,卷积核大小是,则输入特征图的Im2Col过程如下所示,窗口从左到右上到下的顺序在每个输入通道同步滑动,每个窗口内容按行展开成一列,然后再按通道顺序接上填到 buffer对应的列,并且 buffer按照从左到右的顺序填写。
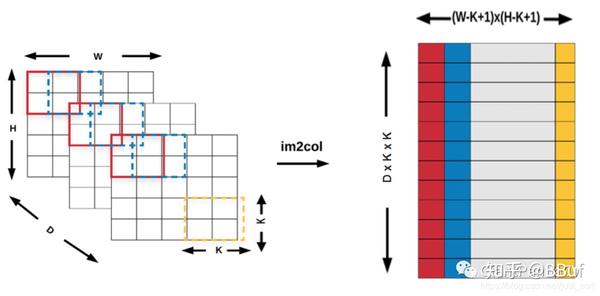
输入特征图的Im2Col
由于这个地方没有padding并且步长是1,那么卷积的输出特征图的高为,同理宽为。所以最后 buffer的宽维度为,高维度则是,最后再把权值Im2Col成,这样卷积就可以直接变成两个二维矩阵的乘法了。
最后再获得了乘积矩阵之后只需要按照通道进行顺序排列就可以获得输出特征图了,这个过程就是Im2Col的逆过程,学名叫作Col2Im,也比较简单就不再赘述了。
3. 如何实现Im2Col
这里我们先做一些约定,变量src表示输入特征图的数据,输入特征图的维度是,输入卷积核的维度是,最后卷积操作执行完之后的输出特征图维度就是。
3.1 对输入特征图进行Im2Col
首先我们对输入特征图进行Im2Col操作,按照之前的介绍可知,我们要得到的结果矩阵的维度是,这个过程只需要窗口从左到右上到下的顺序在每个输入通道同步滑动,每个窗口内容按行展开成一列,然后再按通道顺序接上填到 buffer对应的列,并且 buffer按照从左到右的顺序填写。不难写出这部分的代码实现,这里的src_im2col等价于 buffer:
// 1. im2col
float *src_im2col = new float[outWidth * outHeight * kernelH * kernelW * inChannel];
const int Stride = kernelW * kernelH * outHeight * outWidth;
//const int inSize = inHeight * inWidth;
const int outSize = outHeight * outWidth;
const int kernelSize = kernelH * kernelW;
// inCahnnel x kW x kH
// outWidth x outHeight
for(int cc = 0; cc < inChannel; cc++){
const float *src0 = src + cc * kernelH * kernelW * inChannel;
int dst_idx = Stride * cc;
for(int i = 0; i < kernelH; i++){
for(int j = 0; j < kernelW; j++){
for(int x = 0; x < outHeight; x++){
for(int y = 0; y < outWidth; y++){
int row = x * StrideH + i;
int col = y * StrideW + j;
int ori_idx = row * inWidth + col;
src_im2col[dst_idx] = src0[ori_idx];
dst_idx++;
}
}
}
}
}
3.2 对卷积核进行Im2Col
按照我们第二节的介绍,我们同样可以轻易写出对卷积核进行Im2Col的操作,代码如下:
int Stride = 0;
for(int cc = 0; cc < outChannel; cc++){
int c = cc;
const float* k0 = kernel + c * inChannel * kernelSize;
Stride = kernelSize * inChannel;
float* destptr = dest + c * Stride;
for(int i = 0; i < inChannel * kernelSize; i++){
destptr[0] = k0[0];
destptr += 1;
k0 += 1;
}
}
3.3 优化点之Pack策略
按照第二节介绍的思路,在获取了输入特征图和卷积核的Im2Col变换矩阵之后其实就可以利用Sgemm计算出卷积的结果了。
但是如果直接使用矩阵乘法计算,在卷积核尺寸比较大并且输出特征图通道数也比较大的时候,我们会发现这个时候Im2Col获得矩阵是一个行非常多列非常少的矩阵,在做矩阵乘法的时候访存会变得比较差,从而计算效率边地。这是因为当代CPU架构的某些原因,导致程序在行方向上的处理始终比列方向慢一个档次,所以我们如果能想个办法使得行方向的元素变少,列方向的元素变多这样就可以有效改善缓存达到加速的目的,另外列方向上元素增多更容易让我们发挥Neon指令集的作用。所以,这就是本文将要提到的第一个优化技巧,数据打包(Pack)。
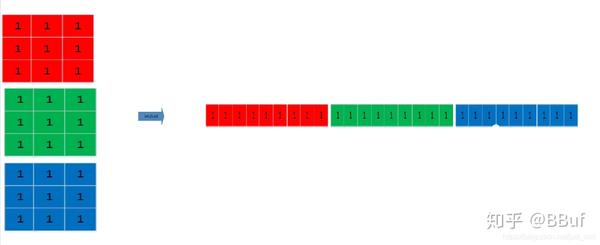
具体来说,对于卷积核我们进行的Pack,如下图所示:
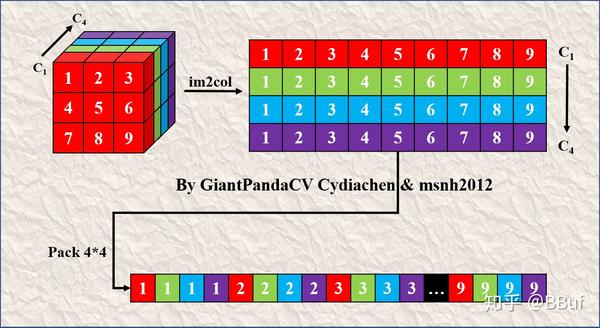
一个3x3x4的卷积核进行Im2Col之后再Pack变成了一行
这是一个的卷积核并且输出通道数为,它经过Im2Col之后首先变成上图的上半部分,然后经过Pack 之后变成了上图的下半部分,即变成了每个卷积核的元素按列方向交织排列。(所谓 的Pack就是在Im2Col获得的二维矩阵的高维度进行压缩,在宽维度进行膨胀,不知道我这种说法是否合适,参考一下下面的图应该很好理解)
这部分的代码也比较容易实现,「另外一个技巧」是,「每次在执行卷积计算时,对于Image的Im2col和Pack每次都会执行,但对于卷积核,Im2col和Pack在任意次只用做一次,所以我们可以在模型初始化的时候提前把卷积核给Pack好,这样就可以节省卷积核Im2Col和Pack耗费的时间」,代码实现如下:
void ConvolutionLayerSgemm::convolutionTransformKernel(float *const &kernel, const int &kernelW, const int &kernelH, float* &dest, const int &inChannel,
const int &outChannel){
int kernelSize = kernelH * kernelW;
int ccOutChannel = 0;
int ccRemainOutChannel = 0;
int Stride = 0;
ccOutChannel = outChannel >> 2;
ccRemainOutChannel = ccOutChannel << 2;
for(int cc = 0; cc < ccOutChannel; cc ++){
int c = cc << 2;
const float* k0 = kernel + c * inChannel * kernelSize;
const float* k1 = kernel + (c + 1) * inChannel * kernelSize;
const float* k2 = kernel + (c + 2) * inChannel * kernelSize;
const float* k3 = kernel + (c + 3) * inChannel * kernelSize;
Stride = 4 * kernelSize * inChannel;
float* destptr = dest + (c / 4) * Stride;
for(int i = 0; i < inChannel * kernelSize; i++){
destptr[0] = k0[0];
destptr[1] = k1[0];
destptr[2] = k2[0];
destptr[3] = k3[0];
destptr += 4;
k0 += 1;
k1 += 1;
k2 += 1;
k3 += 1;
}
}
for(int cc = ccRemainOutChannel; cc < outChannel; cc++){
int c = cc;
const float* k0 = kernel + c * inChannel * kernelSize;
Stride = 4 * kernelSize * inChannel;
float* destptr = dest + (c / 4 + c % 4) * Stride;
for(int i = 0; i < inChannel * kernelSize; i++){
destptr[0] = k0[0];
destptr += 1;
k0 += 1;
}
}
}
注意这个地方如果Pack的时候有拖尾部分,也就是说outChannel不能被4整除时,那么直接按照原始顺序排列即可,后面在Sgemm方法计算的时候需要注意一下。下图展示了一个的卷积核经过Im2Col再经过Pack4x4之后获得的结果,可以看到拖尾那一行是直接复制的,不够的长度直接置0即可。
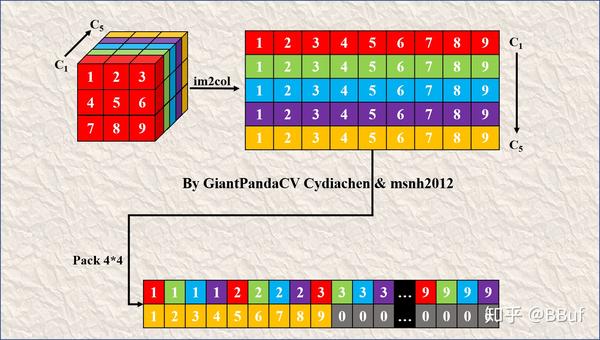
Pack时有拖尾部分的处理
接下来我们继续讲一下对于输入数据的Pack,我这里以对输入数据进行8x8的Pack为例子来讲解输入数据Pack之后应该是什么样子,以及如何和刚才已经4x4Pack好的卷积核执行「矩阵乘法」以完成整个卷积过程。至于为什么这里要使用Pack8x8而不是Pack4x4,因为考虑到MsnhNet后面的版本中需要支持Armv8的实现并且无论如何Pack也基本不影响计算的逻辑。下面我们举个例子来加以说明。
下面展示了一个输入维度为的特征图使用Im2Col进行展开并Pack8x8之后获得结果(卷积核维度为),其中左边代表的是Im2Col后的结果,右边是将其进一步Pack8x8后获得的结果。这个地方由于不能被8整除,所以存在拖尾部分无法进行Pack,即结果图中的第二和第三列,直接顺序放就可以了。
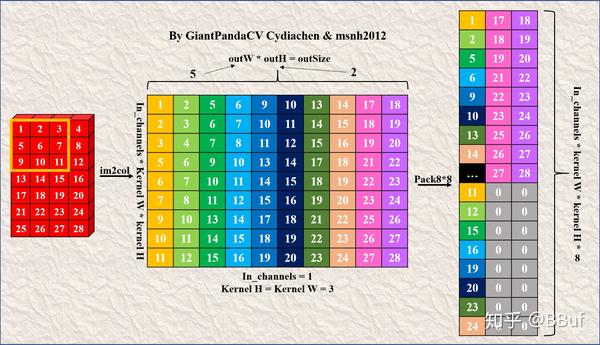
对输入特征图进行Pack8x8
这部分的代码实现也比较简单,如下所示:
// pack 8x8
// preapare
const int packChannel = outSize / 8 + outSize % 8;
const int packHeight = inChannel;
const int packWidth = 8 * kernelSize;
int kernelPackChannel = outChannel / 4 + outChannel % 4;
const int kernelPackHeight = inChannel;
const int kernelPackWidth = 4 * kernelSize;
float *src_im2col_pack = new float[packHeight * packWidth * packChannel];
// pack start
int colCount = outSize >> 3;
int remainColCount = colCount << 3;
#if USE_OMP
#pragma omp parallel for num_threads(OMP_THREAD)
#endif
for(int i = 0; i < colCount; i++){
int newi = i << 3;
const float *src0 = src_im2col;
src0 += newi;
float *packptr = src_im2col_pack + i * packHeight * packWidth;
for(int j = 0; j < inChannel * kernelSize; j ++){
#if USE_NEON
#if __aarch64__
throw Exception(1, "Error: armv8 temporarily not supported!", __FILE__, __LINE__, __FUNCTION__);
#else
asm volatile(
"pld [%0, #256] \n"
"vld1.f32 {d0-d3}, [%0] \n"
"vst1.f32 {d0-d3}, [%1] \n"
: "=r"(src0), // %0
"=r"(packptr) // %1
: "0"(src0),
"1"(packptr)
: "memory", "q0", "q1"
);
#endif
#else
packptr[0] = src0[0];
packptr[1] = src0[1];
packptr[2] = src0[2];
packptr[3] = src0[3];
packptr[4] = src0[4];
packptr[5] = src0[5];
packptr[6] = src0[6];
packptr[7] = src0[7];
#endif
packptr += 8;
src0 += outSize;
}
}
// pack tail
#if USE_OMP
#pragma omp parallel for num_threads(OMP_THREAD)
#endif
for(int i = remainColCount; i < outSize; i++){
const float *src0 = src_im2col;
src0 += i;
float *packptr = src_im2col_pack + (i / 8 + i % 8) * packHeight * packWidth;
for(int j = 0; j < inChannel * kernelSize; j++){
packptr[0] = src0[0];
packptr += 1;
src0 += outSize;
}
}
3.4 优化点之带Pack的矩阵乘法
现在我们已经获得了输入特征图和卷积核的「Im2Col+Pack」操作后的矩阵,那么我们就可以使用矩阵乘法来计算出最后的结果了,即Sgemm算法,但这里因为Pack的原因不能使用OpenBlas标准库。这里介绍一下如何手写一个Sgemm算法。首先Sgemm的接口大概是:
sgemm (int M, int N, int K, float *A, float *B, float *C)
其中输入矩阵A的特征维度是,输入矩阵B的特征维度是,输出矩阵的特征维度是,不考虑任何优化的情况下复杂度是。因为我们这里Pack了数据,所以访存相比于原始版本会变好一些,但计算量实际上还是没变的。除此之外,由于行方向的数据增多我们可以更好的在行方向上进行利用Neon优化使得整个计算过程的效率更好。
所以就目前的情况来说,矩阵A就是我们的「卷积核」经过「Im2Col+Pack4x4」获得的输出矩阵,矩阵B就是我们的输入特征图经过「Im2Col+Pack8x8」之后获得的输出矩阵,然后「矩阵C」就是经过矩阵乘法之后获得的输出特征图了。在实现矩阵乘法的时候,以矩阵A为基准一次处理4行,并且在列方向分别处理4或者8个元素,这个可以结合上面的输入特征图的Im2Col+Pack8x8的示意图来想。最后,对于矩阵A不够4的拖尾部分,进行暴力处理即可。这个地方考虑的是当代典型的CNN架构一般通道数都是的倍数,暂时没有实现拖尾部分的Neon优化,下面先看一下这个算法实现的整体部分,复刻NCNN。
这部分的代码实现如下:
// sgemm (int M, int N, int K, float *A, float *B, float *C)
// A (M x K)
// B (K x N)
// C (M x N)
//int M = outChannel;
int N = outHeight * outWidth;
int K = kernelSize * inChannel;
int ccOutChannel = outChannel >> 2;
int ccRemainOutChannel = ccOutChannel << 2;
#if USE_OMP
#pragma omp parallel for num_threads(OMP_THREAD)
#endif
for(int cc = 0; cc < ccOutChannel; cc++){
int c = cc << 2;
float *destptr0 = dest + c * outSize;
float *destptr1 = dest + (c + 1) * outSize;
float *destptr2 = dest + (c + 2) * outSize;
float *destptr3 = dest + (c + 3) * outSize;
int i = 0;
// N = outHeight*outWidth
for(; i + 7 < N; i = i+8){
const float *ptrB = src_im2col_pack + (i / 8) * packHeight * packWidth;
#if __aarch64__
throw Exception(1, "Error: armv8 temporarily not supported!", __FILE__, __LINE__, __FUNCTION__);
#else
const float *ptrA = kernel_im2col_pack + (c / 4) * kernelPackHeight * kernelPackWidth;
#endif
#if USE_NEON
#if __aarch64__
throw Exception(1, "Error: armv8 temporarily not supported!", __FILE__, __LINE__, __FUNCTION__);
#else
asm volatile(
);
#endif
#else
float sum0[8] = {0};
float sum1[8] = {0};
float sum2[8] = {0};
float sum3[8] = {0};
int j = 0;
// K = kernelSize * inChannel
// 同时计算4行,同时在每一列计算8个输出
for(; j + 7 < K; j = j + 8){
for(int n = 0; n < 8; n++){
sum0[n] += ptrA[0] * ptrB[n];
sum1[n] += ptrA[1] * ptrB[n];
sum2[n] += ptrA[2] * ptrB[n];
sum3[n] += ptrA[3] * ptrB[n];
ptrA += 4;
sum0[n] += ptrA[0] * ptrB[n + 8];
sum1[n] += ptrA[1] * ptrB[n + 8];
sum2[n] += ptrA[2] * ptrB[n + 8];
sum3[n] += ptrA[3] * ptrB[n + 8];
ptrA += 4;
sum0[n] += ptrA[0] * ptrB[n + 16];
sum1[n] += ptrA[1] * ptrB[n + 16];
sum2[n] += ptrA[2] * ptrB[n + 16];
sum3[n] += ptrA[3] * ptrB[n + 16];
ptrA += 4;
sum0[n] += ptrA[0] * ptrB[n + 24];
sum1[n] += ptrA[1] * ptrB[n + 24];
sum2[n] += ptrA[2] * ptrB[n + 24];
sum3[n] += ptrA[3] * ptrB[n + 24];
ptrA += 4;
sum0[n] += ptrA[0] * ptrB[n + 32];
sum1[n] += ptrA[1] * ptrB[n + 32];
sum2[n] += ptrA[2] * ptrB[n + 32];
sum3[n] += ptrA[3] * ptrB[n + 32];
ptrA += 4;
sum0[n] += ptrA[0] * ptrB[n + 40];
sum1[n] += ptrA[1] * ptrB[n + 40];
sum2[n] += ptrA[2] * ptrB[n + 40];
sum3[n] += ptrA[3] * ptrB[n + 40];
ptrA += 4;
sum0[n] += ptrA[0] * ptrB[n + 48];
sum1[n] += ptrA[1] * ptrB[n + 48];
sum2[n] += ptrA[2] * ptrB[n + 48];
sum3[n] += ptrA[3] * ptrB[n + 48];
ptrA += 4;
sum0[n] += ptrA[0] * ptrB[n + 56];
sum1[n] += ptrA[1] * ptrB[n + 56];
sum2[n] += ptrA[2] * ptrB[n + 56];
sum3[n] += ptrA[3] * ptrB[n + 56];
ptrA -= 28;
}
ptrA += 32;
ptrB += 64;
}
// K = kernelSize * inChannel * 4
// 如果是pack4x4那么末尾一定是4的倍数
for(; j < K; j++){
for(int n = 0; n < 8; n++){
sum0[n] += ptrA[0] * ptrB[n];
sum1[n] += ptrA[1] * ptrB[n];
sum2[n] += ptrA[2] * ptrB[n];
sum3[n] += ptrA[3] * ptrB[n];
}
ptrA += 4;
ptrB += 8;
}
for(int n = 0; n < 8; n++){
destptr0[n] = sum0[n];
destptr1[n] = sum1[n];
destptr2[n] = sum2[n];
destptr3[n] = sum3[n];
}
#endif
destptr0 += 8;
destptr1 += 8;
destptr2 += 8;
destptr3 += 8;
}
3.5 优化点之Neon的应用
上面的列方向一次处理多个元素的累乘和累加过程可以进一步使用Neon优化,将上面的一次处理4行,每列一次计算8个输出的代码翻译为Neon汇编代码即可,代码实现以及简要的注释如下:
asm volatile(
"veor q1, q0, q0 \n"
"vdup.f32 q8, d2[0] \n"
"vdup.f32 q9, d2[0] \n"
"vdup.f32 q10, d2[0] \n"
"vdup.f32 q11, d2[0] \n"
"vdup.f32 q12, d2[0] \n"
"vdup.f32 q13, d2[0] \n"
"vdup.f32 q14, d2[0] \n"
"vdup.f32 q15, d2[0] \n"
// r4 = K >> 2
"lsr r4, %12, #2 \n"
// 如果nn等于0,使用beq进行循环跳转,即跳转到循环1
"cmp r4, #0 \n"
"beq loop1 \n"
// for(; nn != 0; nn--) && nn = K >> 2
"loop0: \n"
// kernel q0-q3
"pld [%5, #512] \n"
"vldm %5!, {d0-d7} \n"
// input q4-q7
"pld [%4, #512] \n"
"vldm %4!, {d8-d15} \n"
//calc
// sum0[n] += ptrA[0] * ptrB[n];
"vmla.f32 q8, q4, d0[0] \n"
// sum1[n] += ptrA[1] * ptrB[n];
"vmla.f32 q9, q5, d0[0] \n"
// sum0[n] += ptrA[0] * ptrB[n + 8];
"vmla.f32 q10, q4, d0[1] \n"
// sum1[n] += ptrA[1] * ptrB[n + 8];
"vmla.f32 q11, q5, d0[1] \n"
// sum0[n] += ptrA[0] * ptrB[n + 16];
"vmla.f32 q12, q4, d1[0] \n"
// sum1[n] += ptrA[1] * ptrB[n + 16];
"vmla.f32 q13, q5, d1[0] \n"
// sum0[n] += ptrA[0] * ptrB[n + 24];
"vmla.f32 q14, q4, d1[1] \n"
// sum1[n] += ptrA[1] * ptrB[n + 24];
"vmla.f32 q15, q5, d1[1] \n"
// sum2[n] += ptrA[2] * ptrB[n];
"vmla.f32 q8, q6, d2[0] \n"
// sum3[n] += ptrA[3] * ptrB[n];
"vmla.f32 q9, q7, d2[0] \n"
// sum2[n] += ptrA[2] * ptrB[n + 8];
"vmla.f32 q10, q6, d2[1] \n"
// sum3[n] += ptrA[3] * ptrB[n + 8];
"vmla.f32 q11, q7, d2[1] \n"
// sum2[n] += ptrA[2] * ptrB[n + 16];
"vmla.f32 q12, q6, d3[0] \n"
// sum3[n] += ptrA[3] * ptrB[n + 16];
"vmla.f32 q13, q7, d3[0] \n"
// sum2[n] += ptrA[2] * ptrB[n + 24];
"vmla.f32 q14, q6, d3[1] \n"
// sum3[n] += ptrA[3] * ptrB[n + 24];
"vmla.f32 q15, q7, d3[1] \n"
// ptrA += 4x4
"pld [%4, #512] \n"
"vldm %4!, {d8-d15} \n"
// sum0[n] += ptrA[0] * ptrB[n + 32];
"vmla.f32 q8, q4, d4[0] \n"
// sum1[n] += ptrA[1] * ptrB[n + 32];
"vmla.f32 q9, q5, d4[0] \n"
// sum0[n] += ptrA[0] * ptrB[n + 40];
"vmla.f32 q10, q4, d4[1] \n"
// sum1[n] += ptrA[1] * ptrB[n + 40];
"vmla.f32 q11, q5, d4[1] \n"
// sum0[n] += ptrA[0] * ptrB[n + 48];
"vmla.f32 q12, q4, d5[0] \n"
// sum1[n] += ptrA[1] * ptrB[n + 48];
"vmla.f32 q13, q5, d5[0] \n"
// sum0[n] += ptrA[0] * ptrB[n + 56];
"vmla.f32 q14, q4, d5[1] \n"
// sum1[n] += ptrA[1] * ptrB[n + 56];
"vmla.f32 q15, q5, d5[1] \n"
// sum2[n] += ptrA[2] * ptrB[n + 32];
"vmla.f32 q8, q6, d6[0] \n"
// sum3[n] += ptrA[3] * ptrB[n + 32];
"vmla.f32 q9, q7, d6[0] \n"
// sum2[n] += ptrA[2] * ptrB[n + 40];
"vmla.f32 q10, q6, d6[1] \n"
// sum3[n] += ptrA[3] * ptrB[n + 40];
"vmla.f32 q11, q7, d6[1] \n"
// sum2[n] += ptrA[2] * ptrB[n + 48];
"vmla.f32 q12, q6, d7[0] \n"
// sum3[n] += ptrA[3] * ptrB[n + 48];
"vmla.f32 q13, q7, d7[0] \n"
// sum2[n] += ptrA[2] * ptrB[n + 56];
"vmla.f32 q14, q6, d7[1] \n"
// sum3[n] += ptrA[3] * ptrB[n + 56];
"vmla.f32 q15, q7, d7[1] \n"
"subs r4, r4, #1 \n"
// 第一个for循环的结束,nn>0
"bne loop0 \n"
// 开始写第二个for循环
"loop1: \n"
// K = kernelSize * inChannel * 4
// K >> 2 == inChannel>>2 = inChannel & 3
// 计算完之后进行第三个for循环进行最后的赋值
"and r4, %12, #3 \n"
"cmp r4, #0 \n"
"beq loop3 \n"
"loop2: \n"
// kernel q0 && ptrA += 4
// q0 = [d0, d1] = [ptrA[0], ptrA[1], ptrA[2], ptrA[3]]
"pld [%5, #128] \n"
"vld1.f32 {d0-d1}, [%5]! \n"
// input q4, q5 && ptrB += 8
// q4, q5 = [d8, d9, d10, d11] = [ptrB[0], ..., ptrB[7]]
"pld [%4, #256] \n"
"vld1.f32 {d8-d11}, [%4]! \n"
// for(int n = 0; n < 8; n++){
// sum0[n] += ptrA[0] * ptrB[n];
// sum1[n] += ptrA[1] * ptrB[n];
// sum2[n] += ptrA[2] * ptrB[n];
// sum3[n] += ptrA[3] * ptrB[n];
// }
"vmla.f32 q8, q4, d0[0] \n"
"vmla.f32 q9, q5, d0[0] \n"
"vmla.f32 q10, q4, d0[1] \n"
"vmla.f32 q11, q5, d0[1] \n"
"vmla.f32 q12, q4, d1[0] \n"
"vmla.f32 q13, q5, d1[0] \n"
"vmla.f32 q14, q4, d1[1] \n"
"vmla.f32 q15, q5, d1[1] \n"
"subs r4, r4, #1 \n"
"bne loop2 \n"
// 完成赋值
"loop3: \n"
"vst1.f32 {d16-d19}, [%0] \n"
"vst1.f32 {d20-d23}, [%1] \n"
"vst1.f32 {d24-d27}, [%2] \n"
"vst1.f32 {d28-d31}, [%3] \n"
: "=r"(destptr0), // %0
"=r"(destptr1), // %1
"=r"(destptr2), // %2
"=r"(destptr3), // %3
"=r"(ptrB), // %4
"=r"(ptrA) // %5
: "0"(destptr0),
"1"(destptr1),
"2"(destptr2),
"3"(destptr3),
"4"(ptrB),
"5"(ptrA),
"r"(K) // %12
: "cc", "memory", "r4", "q0", "q1", "q2", "q3", "q4", "q5", "q6", "q7", "q8", "q9", "q10", "q11", "q12", "q13", "q14", "q15"
);
4. 优化效果
下面给出一些测试数据来验证一下此算法的有效性,注意算法的「正确性」笔者已经预先做过一些测试,基本可以保证,不久后此代码也将合并到MsnhNet的下一个发行版本中。
- 下面的测试结果都默认开启了Neon优化,单核A53,Armv7a架构。
- 并且所有的优化方法代码实现都在:https://github.com/msnh2012/Msnhnet 的Arm部分。
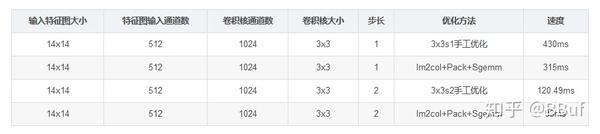
可以看到这里Im2Col+Pack+Sgemm的速度明显快于之前的手动展开版本,在stride为1时优化了100+ms。
下面我们再测一组更大的特征图看一下此算法的表现,一般特征图比较大那么通道数就比较小,我们对应修改一下:
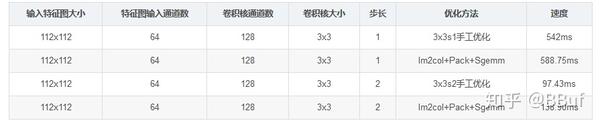
什么鬼?竟然降速了,这是为什么呢?
有一个直观的「猜测」就是当「输入通道数和卷积核尺寸的乘积」也就是卷积核Im2Col获得的矩阵的宽度比较大时,本文介绍的Im2Col+Pack+Sgemm能带来加速效果。在输入特征图通道数较小并且特征图较大时「甚至会比手工优化更慢」,因为这个时候对访存的优化效果很小,因为这个时候Im2Col的矩阵行数和列数差距并不大,这个时候手工优化带来的Cache Miss并不会对卷积的计算带啦很大的影响。因此,此算法并非所有情况适用,需要灵活判断。
本实验进行得比较有限,关于何时切换Sgemm策略进行卷积可以关注MsnhNet的后续实现。
5. 后记
最近花了比较久的时间陆陆续续写完这篇文章并在MsnhNet上实现了这个代码,希望能给想了解Im2Col以及NCNN的Pack优化策略以及如何手动实现一个类Sgemm算法并对其进行优化的读者一些帮助。完整代码可以见:https://github.com/msnh2012/Msnhnet 的Arm端实现部分。另外提供了一个单个OP测试工程,地址为:https://github.com/BBuf/ArmNeonOptimization,目前支持Conv3x3s1,Conv3x3s2,BatchNorm,ConvSgemm 的测试。
6. 致谢
7. 广告时间
MsnhNet是一款基于纯c++的轻量级推理框架,本框架受到darknet启发。
项目地址:https://github.com/msnh2012/Msnhnet
本框架目前已经支持了X86、Cuda、Arm端的推理(支持的OP有限,正努力开发中),并且可以直接将Pytorch模型(后面也会尝试接入更多框架)转为本框架的模型进行部署,欢迎对前向推理框架感兴趣的同学试用或者加入我们一起维护这个轮子。
推荐阅读
更多Tengine相关内容请关注Tengine-边缘AI推理框架专栏。


