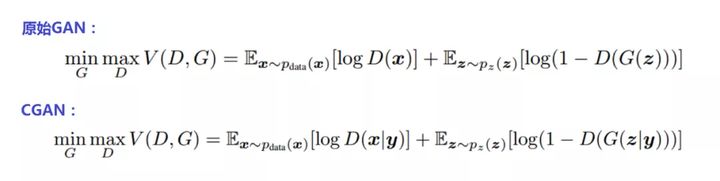从“自由挥洒”到“有的放矢”
1、给GAN加个“按钮”
上一篇《四天搞懂生成对抗网络(一)——通俗理解经典GAN》中,我们实现了一个生成手写数字的GAN 网络。并且,为了完成我的执念——“集齐常用CV数据增广的tricks”(后来发现这个想法太navie了,只要大神们不断造trick发论文,哪有集齐的一天。集不齐也集~~),而尝试使用生成的手写数字样本来提升分类网络的精度,结果自然是缘木求鱼。
因为GAN只是拟合原数据集的像素概率分布,生成的样本并没有提供新的信息以优化模型的分类边界。我理解,样本插值还能优化一下分类边界,原始GAN充其量只能添加一点噪声,或许能增强一点模型泛化能力吧(真做数据增强还得InforGAN、styleGAN这样的才好,能通过潜空间插值对图像做高级语义的增强,这是后话。)。
原始GAN用起来也不方便,为了分别生成0~9的数字,得将原数据集按标签分为10组,每组用一个模型训练,一共需要10个模型。训练时由于每组的数据量少到原来的十分之一,也会发生因样本太少导致模型无法拟合的现象。所以,意欲降伏GAN的大神给原始GAN装了个钮,让GAN乖乖要啥给啥。这个带按钮的改进版就是CGAN。
2、风格迁移网络的“精神始祖”
这个“加个按钮”的思想,不但驯服了CGAN,而且启发了后来的一系列用于风格迁移的GAN,包括Pix2Pix、CycleGAN、StarGAN等。从此,GAN更加的好玩,可以给灰度图片上色修复、把图片变成蓝图或反之、让妹子进入二次元、甚至把照片变成印象派大师的作品(鹿鼎小帅哥就在项目《梵高风格图像生成 一起来玩风格迁移呀!》里展示了一个AI大佬的艺术追求~~)。这也是为什么我将CGAN的项目放到风格迁移GAN系列中来。本来,我是因为看了UGATIT介绍的注意力加强版的CycleGAN,喜欢得不得了,所以想写一个介绍从Pix2Pix到CycleGAN的技能树解锁笔记,敬献给感兴趣的小伙伴们。后来,收集整理资料时了解到CycleGAN的“爹滴”Pix2Pix其实也是一种CGAN,于CGAN的思想是一脉相承的。所以为了搞清来龙去脉,我们先从CGAN讲起...
《梵高风格图像生成 一起来玩风格迁移呀!》AI Studio项目地址:
https://aistudio.baidu.com/ai...
CGAN(Conditional GAN)介绍
1、CGAN的原理
CGAN的全称是Conditional Generative Adversarial Nets,即条件生成对抗网络。故名思议,就是通过添加限制条件,来控制GAN生成数据的特征(类别)。
当我第一次了解了CGAN原理,我惊诧于它给GAN“加按钮”的方法竟然如此简单粗暴,要做仅仅就是“把按钮加上去”——训练时将控制生成类别的标签连同噪声一起送进生成器的输入端,这样在预测时,生成器就会同样根据输入的标签生成指定类别的图片了。判别器的处理也是一样,仅仅在输入加上类别标签就可以了。
那么,为什么加了标签,CGAN就乖乖听话、要啥给啥了呢?原理也是十分简单,我们知道GAN要干的就是拟合数据的概率分布,而CGAN拟合的就是条件下的概率分布。
看看原始GAN和CGAN的公式对比:
原始GAN的优化目标是在判别器最大化真实数据与生成数据差异的情况下,最小化这个差距(详细的解释请参考《四天搞懂生成对抗网络(一)——通俗理解经典GAN》),以训练生成器,能够将输入的正态分布的随机噪声z尽可能完美的映射为训练集数据的概率分布。
而上面CGAN公式中的条件y就是咱给GAN装的“钮”。加上了这个条件按钮,GAN优化的概率期望分布公式就变成了CGAN优化的条件概率期望分布公式。即CGAN优化的目标是:在条件Y下,在判别器最大化真实数据与生成数据差异的情况下,最小化这个差距。训练CGAN的生成器时要同时送入随机噪声z和和条件y(在本项目中y就是MNIST手写数字数据集的数字标签)。就是这么简单!
其实,在《四天搞懂生成对抗网络(一)——通俗理解经典GAN》中,我们介绍判别网络与生成网络的区别时曾经分析过:判别网络学习的是输入x条件下的条件概率分布p(y|x),而生成网络学习的是概率分布p(x)。那么我们给生成网络也加上个条件y,学习条件y下的条件概率分布p(x|y)就是CGAN了。
详细的理论推导请参考原论文《Conditional Generative Adversarial Nets》:
https://arxiv.org/pdf/1411.17...
那么,下面我们就来看看装了按钮(条件y)的CGAN到底有何不同。
2、CGAN的结构
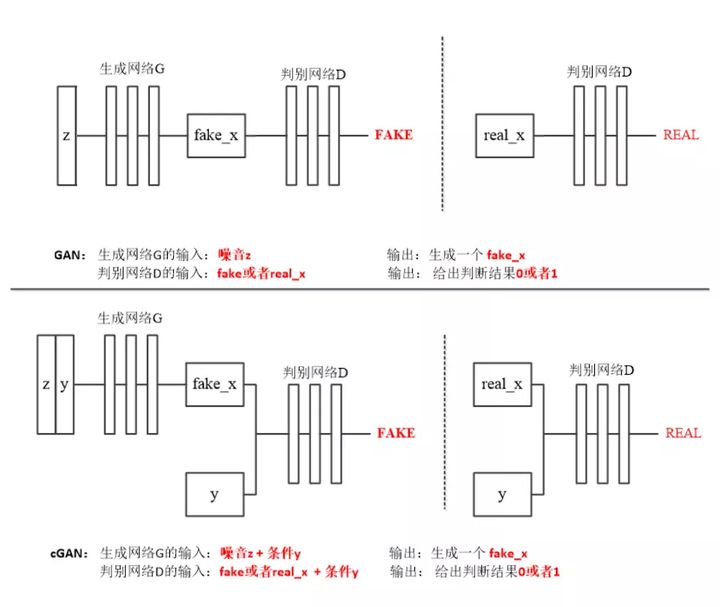
CGAN设计巧妙,而结构也十分简单、清晰,与经典GAN只有输入部分稍许不同。我们看看原始GAN与CGAN的结构对比(包括生成器和判别器),上半部份的是经典GAN,下半部分是CGAN:
我们先回顾下经典GAN的结构流程(如上图上半部份所示):
训练判别器。将噪声z送入生成器,输出fake_x;将fake_x送入判别器,在更新判别器参数时尝试拉近判别器的输出与真标签1的距离,即最小化判别器输出与真标签1的交叉熵损失。再将真图片送入判别器,更新判别器参数时尝试拉近判别器的输出与假标签0的距离,即最小化判别器输出与假标签0的交叉熵损失。这个过程中,用真、“假”图片训练判别器的顺序不必需固定,真、假标签取值0、1也无需固定(可相反,效果没有区别)。要注意的是,训练判别器的过程中,只更新判别器参数,不更新生成器参数。
训练生成器。生成器训练的过程和判别器基本一样,只是将生成器输出的“假图片”送入判别器后,将判别器的输出与真标签(1)拉近。目的就是,使生成器参数更新的方向朝着“骗过判别器的目标”进行,也就是所谓“对抗过程”。当然判别器出掌(判别器更新参数)时,生成器不还手(生成器不更新参数),轮到生成器还手(生成器更新参数)时,判别器也得双手背后(判别器不更新参数)。不然就打成一团,谁也看不到招式(无法正确更新参数,提高生成能力)了~~
我们再看下CGAN给GAN加的“料”(如上图下半部份所示):
先看判别器。如图,无论是给判别器送入真图片还是生成器生成的假图片时,都要加上个“条件y”,也就是分类标签。判别器输出没有变化仍然只是判断输入图片的真假。老实说,当时我曾想:既然咱都conditional GAN了,这个判别器是不是要输出分类标签y来训练Condition那部分?但转念一想,不行,判别器还是得判别真假,不然没法和生成器对抗了。BUT,后来我发现还真有走这个路线的GAN,叫InfoGAN。这个InfoGAN给生成器配了两个判别器,一个判真假,一个分类别。
再看生成器。生成器的输入除了随机噪声z外,也加入了“条件y”。到这儿,我又想:既然有了条件标签,就不用输入噪声z了吧~。答案当然是,不行!因为,噪声z的维度是和生成器输出图片的尺寸、复杂度相关的。本项目中输出图片尺寸是28×28=784。按理说模型进行映射的输入、输出尺寸应该是相等的。但是输出图片只是手写数字,规律比较简单,输入的尺寸可以进行一定程度的压缩。一般噪声z的维度为几十到一百就能生成比较理想的图片细节,如果太低会导致生成器拟合能力不足,生成图片质量低下。条件z只是一个取值0~9的维度为一的向量,模型拟合像素概率分布的效果可想而知。后面我们介绍的Pix2Pix模型的输入是一张和输出尺寸相同的图片,就不再输入噪声z了。
CGAN需要注意的一点是:输入的条件标签y不但要在输入时与噪声z融合在一起,在生成器和判别器的每一层输入里都要与特征图相融合,才能让模型“学好条件y”。不然,标签可能不灵~
下面就是我最喜欢的部分了——跑代码
CGAN码上实现
1、数据读取
数据读取部分与原始GAN略有不同。原始GAN只需读入图片数据,而CGAN需要同时读取图片数字的label标签,一起送入判别器和生成器进行训练。
## 定义数据读取
import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph import Conv2D, Pool2D, Linear, Conv2DTranspose
import numpy as np
import matplotlib.pyplot as plt
# 噪声维度
Z_DIM = 100
BATCH_SIZE = 128
# BATCH_SIZE = 3 # debug
# 噪声生成,通过由噪声来生成假的图片数据输入。
def z_reader():
while True:
yield np.random.normal(0.0, 1.0, (Z_DIM, 1, 1)).astype('float32')
# 生成真实图片reader
mnist_generator = paddle.batch(
paddle.reader.shuffle(paddle.dataset.mnist.train(), 30000), batch_size=BATCH_SIZE)
# 生成假图片的reader
z_generator = paddle.batch(z_reader, batch_size=BATCH_SIZE)
import matplotlib.pyplot as plt
%matplotlib inline
data_tmp = next(mnist_generator())
print('一个batch图片数据的形状:batch_size =', len(data_tmp), ', data_shape =', data_tmp[0][0].shape, ', num = ', data_tmp[0][1])
plt.imshow(data_tmp[0][0].reshape(28, 28))
plt.show()
z_tmp = next(z_generator())
print('一个batch噪声z的形状:batch_size =', len(z_tmp), ', data_shape =', z_tmp[0].shape)
一个batch图片数据的形状:batch_size = 128 , data_shape = (784,) , num = 7
一个batch噪声z的形状:batch_size = 128 , data_shape = (100, 1, 1) 2、生成器与判别器
这部分是CGAN代码的重点。加入的标签y不是来参观旅游的(是来当产品经理的~~)。它要作为条件约束来限制生成器的输出,就要深入到模型各层参与训练过程。
参与的方法就是,将标签y拼接到生成器和判别器的每层网络生成的特征图上。拼接时 注意以下两点:
噪声拼接使用Paddle框架的fluid.layers.concat()函数实现。为了使代码清晰,我们将拼接特征图(包括全连接层和噪声输出的一维特征图 与 卷积层输出的和原始图片的二维特征图)与噪声的代码封装在conv_concatenate()函数里。
在生成器与判别器的前向计算过程中,除了最后一层的输出,生成器输入的噪声、判别器输入的图片都要拼接噪声。
(注:原论文中作者将标签embedding在了长度为10的one-hot向量上,本项目中则直接使用了长度为1的float32类型的数值(0~9的分类标签)与特征图拼接)
## 定义CGAN
# 定义特征图拼接
def conv_concatenate(x, y):
# print('---', x.shape, y.shape)
# y = fluid.dygraph.to_variable(y.numpy().astype('float32'))
if len(x.shape) == 2: # 给全连接层输出的特征图拼接噪声
y = fluid.layers.reshape(y, shape=[x.shape[0], 1])
ones = fluid.layers.fill_constant(y.shape, dtype='float32', value=1.0)
elif len(x.shape) == 4: # 给卷积层输出的特征图拼接噪声
y = fluid.layers.reshape(y, shape=[x.shape[0], 1, 1, 1])
ones = fluid.layers.fill_constant(x.shape, dtype='float32', value=1.0)
x = fluid.layers.concat([x, ones * y], axis=1)
# print(ones.shape, x.shape, y.shape, '---')
return x
# 定义生成器
class G(fluid.dygraph.Layer):
def __init__(self, name_scope):
super(G, self).__init__(name_scope)
name_scope = self.full_name()
# 第一组全连接和BN层
self.fc1 = Linear(input_dim=100+1, output_dim=1024)
self.bn1 = fluid.dygraph.BatchNorm(num_channels=1024, act='relu')
# 第二组全连接和BN层
self.fc2 = Linear(input_dim=1024+1, output_dim=128*7*7)
self.bn2 = fluid.dygraph.BatchNorm(num_channels=128*7*7, act='relu')
# 第一组转置卷积运算
self.convtrans1 = Conv2DTranspose(256, 64, 4, stride=2, padding=1)
self.bn3 = fluid.dygraph.BatchNorm(64, act='relu')
# 第二组转置卷积运算
self.convtrans2 = Conv2DTranspose(128, 1, 4, stride=2, padding=1, act='relu')
def forward(self, z, label):
z = fluid.layers.reshape(z, shape=[-1, 100])
z = conv_concatenate(z, label) # 拼接噪声和label
y = self.fc1(z)
y = self.bn1(y)
y = conv_concatenate(y, label) # 拼接特征图和label
y = self.fc2(y)
y = self.bn2(y)
y = fluid.layers.reshape(y, shape=[-1, 128, 7, 7])
y = conv_concatenate(y, label) # 拼接特征图和label
y = self.convtrans1(y)
y = self.bn3(y)
y = conv_concatenate(y, label) # 拼接特征图和label
y = self.convtrans2(y)
return y
# 定义判别器
class D(fluid.dygraph.Layer):
def __init__(self, name_scope):
super(D, self).__init__(name_scope)
name_scope = self.full_name()
# 第一组卷积池化
self.conv1 = Conv2D(num_channels=2, num_filters=64, filter_size=3)
self.bn1 = fluid.dygraph.BatchNorm(num_channels=64, act='leaky_relu')
self.pool1 = Pool2D(pool_size=2, pool_stride=2)
# 第二组卷积池化
self.conv2 = Conv2D(num_channels=128, num_filters=128, filter_size=3)
self.bn2 = fluid.dygraph.BatchNorm(num_channels=128, act='leaky_relu')
self.pool2 = Pool2D(pool_size=2, pool_stride=2)
# 全连接输出层
self.fc1 = Linear(input_dim=128*5*5+1, output_dim=1024)
self.bnfc1 = fluid.dygraph.BatchNorm(num_channels=1024, act='leaky_relu')
self.fc2 = Linear(input_dim=1024+1, output_dim=1)
def forward(self, img, label):
y = conv_concatenate(img, label) # 拼接输入图片和label
y = self.conv1(y)
y = self.bn1(y)
y = self.pool1(y)
y = conv_concatenate(y, label) # 拼接特征图和label
y = self.conv2(y)
y = self.bn2(y)
y = self.pool2(y)
y = fluid.layers.reshape(y, shape=[-1, 128*5*5])
y = conv_concatenate(y, label) # 拼接特征图和label
y = self.fc1(y)
y = self.bnfc1(y)
y = conv_concatenate(y, label) # 拼接特征图和label
y = self.fc2(y)
return y
## 测试生成网络G和判别网络D
with fluid.dygraph.guard():
g_tmp = G('G')
l_tmp = fluid.dygraph.to_variable(np.array([x[1] for x in data_tmp]).astype('float32'))
tmp_g = g_tmp(fluid.dygraph.to_variable(np.array(z_tmp)), l_tmp).numpy()
print('生成器G生成图片数据的形状:', tmp_g.shape)
plt.imshow(tmp_g[0][0])
plt.show()
d_tmp = D('D')
tmp_d = d_tmp(fluid.dygraph.to_variable(tmp_g), l_tmp).numpy()
print('判别器D判别生成的图片的概率数据形状:', tmp_d.shape)生成器G生成图片数据的形状:(128, 1, 28, 28)
判别器D判别生成的图片的概率数据形状:(128, 1)
3、辅助函数
用于打印输出训练、预测图片
## 定义显示图片的函数,构建一个18*n大小(n=batch_size/16)的图片阵列,把预测的图片打印到note中。
import matplotlib.pyplot as plt
%matplotlib inline
def show_image_grid(images, batch_size=128, pass_id=None):
fig = plt.figure(figsize=(8, batch_size/32))
fig.suptitle("Pass {}".format(pass_id))
gs = plt.GridSpec(int(batch_size/16), 16)
gs.update(wspace=0.05, hspace=0.05)
for i, image in enumerate(images):
ax = plt.subplot(gs[i])
plt.axis('off')
ax.set_xticklabels([])
ax.set_yticklabels([])
ax.set_aspect('equal')
plt.imshow(image[0], cmap='Greys_r')
plt.show()
show_image_grid(tmp_g, BATCH_SIZE)4、训练过程
CGAN的训练过程与原始GAN基本没有区别,只是因为要让模型输出的数字较好的受输入标签y的约束(避免输出的数字错乱),需要较长的训练迭代步数,使模型更好的学习标签y与生成数字的对应关系。所以,CGAN采用了LSGAN的loss来稳定训练过程,避免长时训练时发生模式崩溃。具体做法如下:
去掉判别器最后一层的sigmoid激活函数。
使用最小二乘损失代替原来的交叉熵损失。
替换loss函数在代码上只需修改一句:将原来的
1 real_cost = fluid.layers.sigmoid_cross_entropy_with_logits(p_real, ones)替换为
1 real_cost = (p_real - ones) ** 2 #lsgan本项目中每轮迭代时,分别使用真假数据各训练一次判别器,再加上训练一次生成器。所以上面loss函数的修改要在这三处全部实施。
## 训练CGAN
from visualdl import LogWriter
import time
import random
def train(mnist_generator, epoch_num=10, batch_size=128, use_gpu=True, load_model=False):
# with fluid.dygraph.guard():
place = fluid.CUDAPlace(0) if use_gpu else fluid.CPUPlace()
with fluid.dygraph.guard(place):
# 模型存储路径
model_path = './output/'
d = D('D')
d.train()
g = G('G')
g.train()
# 创建优化方法
g_optimizer = fluid.optimizer.AdamOptimizer(learning_rate=2e-4, parameter_list=g.parameters())
d_optimizer = fluid.optimizer.AdamOptimizer(learning_rate=2e-4, parameter_list=d.parameters())
# 读取上次保存的模型
if load_model == True:
g_para, g_opt = fluid.load_dygraph(model_path+'g')
d_para, d_opt = fluid.load_dygraph(model_path+'d')
g.load_dict(g_para)
g_optimizer.set_dict(g_opt)
d.load_dict(d_para)
d_optimizer.set_dict(d_opt)
iteration_num = 0
print('Start time :', time.strftime("%Y-%m-%d %H:%M:%S", time.localtime()), 'start step:', iteration_num + 1)
for epoch in range(epoch_num):
for i, real_data in enumerate(mnist_generator()):
# 丢弃不满整个batch_size的数据
if(len(real_data) != BATCH_SIZE):
continue
iteration_num += 1
'''
判别器d通过最小化输入真实图片时判别器d的输出与真值标签ones的交叉熵损失,来优化判别器的参数,
以增加判别器d识别真实图片real_image为真值标签ones的概率。
'''
# 将MNIST数据集里的图片读入real_image,将真值标签ones用数字1初始化
ri = np.array([x[0] for x in real_data]).reshape(-1, 1, 28, 28)
rl = np.array([x[1] for x in real_data]).astype('float32')
real_image = fluid.dygraph.to_variable(np.array(ri))
real_label = fluid.dygraph.to_variable(rl)
ones = fluid.dygraph.to_variable(np.ones([len(real_image), 1]).astype('float32'))
# 计算判别器d判断真实图片的概率
p_real = d(real_image, real_label)
# 计算判别真图片为真的损失
# real_cost = fluid.layers.sigmoid_cross_entropy_with_logits(p_real, ones)
real_cost = (p_real - ones) ** 2 #lsgan
real_avg_cost = fluid.layers.mean(real_cost)
'''
判别器d通过最小化输入生成器g生成的假图片g(z)时判别器的输出与假值标签zeros的交叉熵损失,
来优化判别器d的参数,以增加判别器d识别生成器g生成的假图片g(z)为假值标签zeros的概率。
'''
# 创建高斯分布的噪声z,将假值标签zeros初始化为0
z = next(z_generator())
z = fluid.dygraph.to_variable(np.array(z))
zeros = fluid.dygraph.to_variable(np.zeros([len(real_image), 1]).astype('float32'))
# 判别器d判断生成器g生成的假图片的概率
p_fake = d(g(z, real_label), real_label)
# fl = rl
# for i in range(batch_size):
# fl[i] = random.randint(0, 9)
# fake_label = fluid.dygraph.to_variable(fl)
# p_fake = d(g(z, fake_label), fake_label)
# 计算判别生成器g生成的假图片为假的损失
# fake_cost = fluid.layers.sigmoid_cross_entropy_with_logits(p_fake, zeros)
fake_cost = (p_fake - zeros) ** 2 #lsgan
fake_avg_cost = fluid.layers.mean(fake_cost)
# 更新判别器d的参数
d_loss = real_avg_cost + fake_avg_cost
d_loss.backward()
d_optimizer.minimize(d_loss)
d.clear_gradients()
'''
生成器g通过最小化判别器d判别生成器生成的假图片g(z)为真的概率d(fake)与真值标签ones的交叉熵损失,
来优化生成器g的参数,以增加生成器g使判别器d判别其生成的假图片g(z)为真值标签ones的概率。
'''
# 生成器用输入的高斯噪声z生成假图片
fake = g(z, real_label)
# 计算判别器d判断生成器g生成的假图片的概率
p_fake = d(fake, real_label)
# 使用判别器d判断生成器g生成的假图片的概率与真值ones的交叉熵计算损失
# g_cost = fluid.layers.sigmoid_cross_entropy_with_logits(p_fake, ones)
g_cost = (p_fake - ones) ** 2 #lsgan
g_avg_cost = fluid.layers.mean(g_cost)
# 反向传播更新生成器g的参数
g_avg_cost.backward()
g_optimizer.minimize(g_avg_cost)
g.clear_gradients()
if(iteration_num % 100 == 0):
print('epoch =', epoch, ', batch =', i, ', d_loss =', d_loss.numpy(), 'g_loss =', g_avg_cost.numpy())
show_image_grid(fake.numpy(), BATCH_SIZE, epoch)
print('End time :', time.strftime("%Y-%m-%d %H:%M:%S", time.localtime()), 'End Step:', iteration_num)
# 存储模型
fluid.save_dygraph(g.state_dict(), model_path+'g')
fluid.save_dygraph(g_optimizer.state_dict(), model_path+'g')
fluid.save_dygraph(d.state_dict(), model_path+'d')
fluid.save_dygraph(d_optimizer.state_dict(), model_path+'d')
# train(mnist_generator, epoch_num=1, batch_size=BATCH_SIZE, use_gpu=True)
train(mnist_generator, epoch_num=1, batch_size=BATCH_SIZE, use_gpu=True, load_model=True)
# train(mnist_generator, epoch_num=20, batch_size=BATCH_SIZE, use_gpu=True, load_model=True) #11m
# train(mnist_generator, epoch_num=800, batch_size=BATCH_SIZE, use_gpu=True, load_model=True) #440mStart time : 2020-11-09 18:34:07 start step: 1
epoch = 0 , batch = 99 , d_loss = [0.00953399] g_loss = [1.1064374]
epoch = 0 , batch = 199 , d_loss = [0.01267804] g_loss = [0.87320054]
epoch = 0 , batch = 299 , d_loss = [0.01677028] g_loss = [0.9350312]
epoch = 0 , batch = 399 , d_loss = [0.01072838] g_loss = [1.0959808]
End time : 2020-11-09 18:34:35 End Step: 468
5、预测过程
赶快用训练好的模型,按照标签约束分别生成数字0~9看看效果吧。
## 使用CGAN分别生成数字0~9
def infer(batch_size=128, num=0, use_gpu=True):
place = fluid.CUDAPlace(0) if use_gpu else fluid.CPUPlace()
with fluid.dygraph.guard(place):
# 模型存储路径
model_path = './output/'
g = G('G')
g.eval()
# 读取上次保存的模型
g_para, g_opt = fluid.load_dygraph(model_path+'g')
g.load_dict(g_para)
# g_optimizer.set_dict(g_opt)
z = next(z_generator())
z = fluid.dygraph.to_variable(np.array(z))
label = fluid.layers.fill_constant([batch_size], dtype='float32', value=float(num))
fake = g(z, label)
show_image_grid(fake.numpy(), batch_size, -1)
for i in range(10):
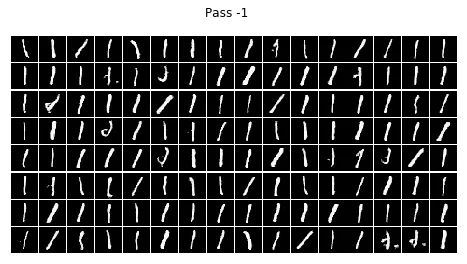
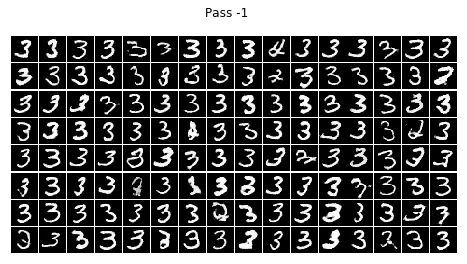
infer(batch_size=BATCH_SIZE, num=i)结论
不看广告看疗效~~CGAN已经完全治好了原始GAN的数字混乱,生成的数字都乖乖的按照输入的标签齐刷刷的立正站好......
在训练的过程中我发现,训练个二十轮后,CGAN就已经能够像他哥原始GAN那样生成比较清晰的数字,但标签控对数字的控制还很不好,按钮时灵时不灵。生成一个batch size的数字,少一半都站错了队。在训练一个晚上后(轮数没记录下来,可以按时间估算),模型总算总算学会了让生成的数字们按标签y站好队。
但是,生成的结果还是不完美。有些生成的数字是四不像。这点还可以理解,毕竟有些训练集里的字符本身就不是很清楚规整,所以生成的也是那副德行。还有些字符清清楚楚就不属于生他的标签(抱错了吧,哈哈),比如标签为4的那一组,好几个3恬不知耻的站在那里碍眼。我推测原因可能如下:
可能和生成四不像的原因一样,是数据集标注错误导致的。这样的话就不是模型的问题了,起码不是模型精度的问题。
也可能是模型训练得还不充分,再训练一个晚上也许就调教好了。我真是觉得GAN模型不像分类模型那么好炼,火大火小(过拟合欠拟合)一目了然,GAN同时训练至少两个模型,就像水多加面、面多加水,到底熟没熟经常尝不出来~~
还有一种可能就是控制变量y在训练的过程中比例占得太小了,输入的噪声100维,拼接上了1维y变成101维,控制变量在特征中所占比例才1%,拼接入全连接层特征图则比例更低,拼接入卷积层特征图则比例更更低。我想如果像原论文那样采用one-hot编码会不会好一点,控制变量y的权重可以扩大10倍。
欢迎各位同学大佬交流心得,指点迷津,在Deep Learnning的道路上互相拔扯,拉人出坑,功德无量~~
这个CGAN项目我们给GAN“加个钮”,下个Pix2Pix项目我们就试着给GAN“画张图”~~