本作品介绍参与极术社区的有奖征集|分享研电赛作品扩大影响力,更有重磅电子产品免费领取!
论文题目:
基于ADRC的双轴反作用轮自平衡杆
Dual-axis reaction wheel self-balancing rod based on ADRC
参赛单位: 广西科技大学
队伍名称: 平衡空间
指导老师: 文家燕
参赛队员: 温林荣、陈家宝、闻海潮
完成时间: 2021.6.19
本篇并非完全由本人所写,本人只做了原理推导部分,工程实现部分是拼凑起来的。对这个课题感兴趣的读者可以移步https://blog.csdn.net/qq_4551... ,那里有详细的MATLAB代码。
摘 要
倒立摆系统因其非线性结构特点,在实际控制问题中具有重要地位,控制三维自由物体和机器人的方向与速度是一项非常困难的任务。由于各种限制,传统的致动器应用效果比较困难。在这种情况下,反作用轮的使用变得突出。基于反作用轮的系统被广泛应用于航天器、运输系统和其他类似系统的定向、协调和平衡。本研究设计、制造并控制了基于双轴自平衡反应轮的倒立摆系统,该系统是许多复杂系统的基础。结合双轴反作用论倒立摆动力学模型的多变量、强耦合问题,进行控制方案的分析与论证,最终选择自抗扰控制。本作品的创新之处是要实现倒立摆的大角度回正平衡控制,即当摆杆的初始姿态偏离竖直状态的角度较大时,摆杆通过两个反作用轮的调节最终能够回到竖直状态并稳定平衡。最后通过STM32F103系列产品作为主控芯片,完成了对机器人实物的设计和实现,并具有良好的抗干扰性能。
关键字:动量轮、自平衡、自抗扰控制
Abstract
The inverted pendulum system plays an important role in actual control problems due to its non-linear structural characteristics. It is a very difficult task to control the direction and speed of three-dimensional free objects and robots. Due to various limitations, the application effect of traditional actuators is more difficult. In this case, the use of reaction wheels becomes prominent. Systems based on reaction wheels are widely used in the orientation, coordination and balance of spacecraft, transportation systems and other similar systems. This research designed, manufactured and controlled an inverted pendulum system based on a dual-axis self-balancing reaction wheel, which is the basis of many complex systems. Combining with the multi-variable and strong coupling problem of the dual-axis reaction theory inverted pendulum dynamic model, the control scheme is analyzed and demonstrated, and the auto disturbance rejection control is finally selected. The innovation of this work is to realize the large-angle return balance control of the inverted pendulum, that is, when the initial posture of the pendulum rod deviates from the vertical state by a large angle, the pendulum rod can finally return to the vertical position through the adjustment of the two reaction wheels Straight state and stable balance. Finally, the STM32F103 series products are used as the main control chip to complete the design and realization of the robot, and it has good anti-interference performance.
KEYWORDS:Momentum wheel, self-balancing, auto disturbance rejection control
目 录
第1章 绪论 1
1.1研究背景及其意义 1
1.2设计难点与创新 2
1.3本文的主要研究内容及结构安排 2
第2章 方案的设计与论证 3
2.1双反作用轮倒立摆定点自平衡动力学模型 3
2.2控制系统设计方案 6
2.2.1自抗扰控制原理 6
2.2.2系统解耦 6
2.2.3 自抗扰控制控制器算法 7
2.2.4 自抗扰控制器参数整定 8
第3章 硬件系统设计 9
3.1机械结构的设计 9
3.1.1电机的选择 9
3.1.2结构设计 10
3.2硬件设计 11
3.2.1设计总览 11
3.2.2 各个功能模块的具体结构和作用 12
3.3 系统总成 16
第4章 软件系统设计及分析 16
4.1软件描述部分 16
4.1.1电机速度反馈信号处理程序 17
4.1.2陀螺仪姿态数据处理程序 18
4.2实验装置测试及结果分析 18
第5章 总结 19
参考文献 20
第1章 绪论
1.1研究背景及其意义
早在20世纪60年代,人们就开始了对倒立摆系统的研究。1966 年Schacfer和Cannon应用Bang-Bang控制理论,将一个曲轴稳定于倒置位置。到了20世纪60年代后期,倒立摆作为一个典型不稳定、非线性的例证被提出。自此,对于倒立摆系统的研究便成了控制界关注的焦点。倒立摆的种类很多,有悬挂式倒立摆、平行倒立摆、环形倒立摆、平面倒立摆;倒立摆的级数可以是一级、二级、三级、四级乃至多级;倒立摆的运动轨道可以是水平的或是倾斜的;控制电机可以是单电机,也可以是多级电机。
倒立摆控制系统是一个复杂的、不稳定的、非线性系统,是进行控制理论教学及开展各种控制实验的理想实验平台。对倒立摆系统的研究能有效的反映控制中的许多典型问题:如非线性问题、鲁棒性问题、镇定问题、随动问题以及跟踪问题等。通过对倒立摆的控制,用来检验新的控制方法是否有较强的处理非线性和不稳定性问题的能力。同时,其控制方法在军工、航天、机器人和一般工业过程领域中都有着广泛的用途,如:(1)机器人的站立与行走类似双倒立摆系统,尽管第一台机器人在美国问世至今已有三十年的历史,机器人的关键技术--机器人的行走控制至今仍未能很好解决。
(2)在火箭等飞行器的飞行过程中,为了保持其正确的姿态,要不断进行实时控制。
(3)通信卫星在预先计算好的轨道和确定的位置上运行的同时,要保持其稳定的姿态,使卫星天线一直指向地球,使它的太阳能电池板一直指向太阳。
(4)侦察卫星中摄像机的轻微抖动会对摄像的图像质量产生很大的影响,为了提高摄像的质量,必须能自动地保持伺服云台的稳定,消除震动。
(5)为防止单级火箭在拐弯时断裂而诞生的柔性火箭(多级火箭),其飞行姿态的控制也可以用多级倒立摆系统进行研究。
对倒立摆这样的一个典型被控对象进行研究,无论在理论上和方法上都具有重要意义。不仅由于其级数增加而产生的控制难度是对人类控制能力的有力挑战,更重要的是实现其控制稳定的过程中不断发现新的控制方法,探索新的控制理论,并进而将新的控制方法应用到更广泛的受控对象中。各种控制理论和方法都可以在这里得以充分实践,并且可以促成相互间的有机结合。而基于反作用轮的倒立摆系统,人们已经做了很多研究。文献[1]对反作用轮式倒立摆的线性控制进行了研究。文献[2]对双轴倒立摆的非线性控制进行了研究。文献[3]对基于模糊逻辑的控制进行了研究。Spong等人在[4]中对基于反作用轮的系统进行了建模和控制研究。反作用轮可以利用旋转轮的惯性向它们所连接的物体施加扭矩,通过这种方式,它们可以改变物体的方向。倒立摆系统有非常丰富的背景,它们经常被用于测试、实现和比较新的控制概念和理论。
一般来说,反作用轮用于在没有重力和摩擦力的空间中控制航天器的方向,而不使用火箭燃料或任何其他致动器。基本工作原理基于牛顿第三定律:“对于每一个动作,都有一个相等且相反的反作用力。”在此基础上,附着在任何电机上的反作用轮都会产生一个动量,该动量与角动量相等且相反,因为动量守恒定律取决于其角速度。反作用轮只能围绕质心产生动量。因此,它们不能产生平移运动。
就像任何其他系统一样,如果没有施加外部扭矩,角动量将是守恒的。因此,通过用反作用轮向下降方向施加反扭矩,可以平衡系统。为此目的而控制的马达使摆锤围绕摆锤接触地面的点保持平衡。
1.2设计难点与创新
单级倒立摆根据获得反作用力的方式大致可以分为两类,一类是通过摆杆底端旋转滚轮与地面接触产生反作用力与力矩来改变姿态,另一类是通过摆杆顶部的旋转飞轮加减速来接收地面的反作用力与力矩。前者在调整平衡的过程中会在支撑面上移动,而后者是固定支撑点的。本作品是固定支撑点的倒立摆如图1所示,并且摆杆的运动自由度是3,如图2所示的姿态描述方式。本作品的创新之处是要实现倒立摆的大角度回正平衡控制,即当摆杆的初始姿态偏离竖直状态的角度较大时,摆杆通过两个反作用轮的调节最终能够回到竖直状态并稳定平衡。本作品的难点是控制算法的设计。由于三自由度的倒立摆是一个多输入多输出、非线性请耦合的控制系统,一直以来都是控制领域的难题。传统的双反作用轮定点倒立摆平衡控制方法是小偏角的直接去耦合法,就是将摆杆三自由度的运动简化成只考虑一个自由度的摆动来建立动力学模型和设计控制器。以成熟的线性系统理论为基础,这种控制器的算法较为简单,缺点是倾角回正范围太小。要扩大可回正倾角需要考虑大角度时的非线性和耦合效应,需要用到解耦合相关的理论。
1.3本文的主要研究内容及结构安排
第1章 主要介绍本设计的研究背景及难点与创新
第2章 主要建立模型说明系统方案的设计
第3章 主要介绍硬件系统设计
第4章 主要介绍软件系统设计及分析
第2章 方案的设计与论证
2.1双反作用轮倒立摆定点自平衡动力学模型
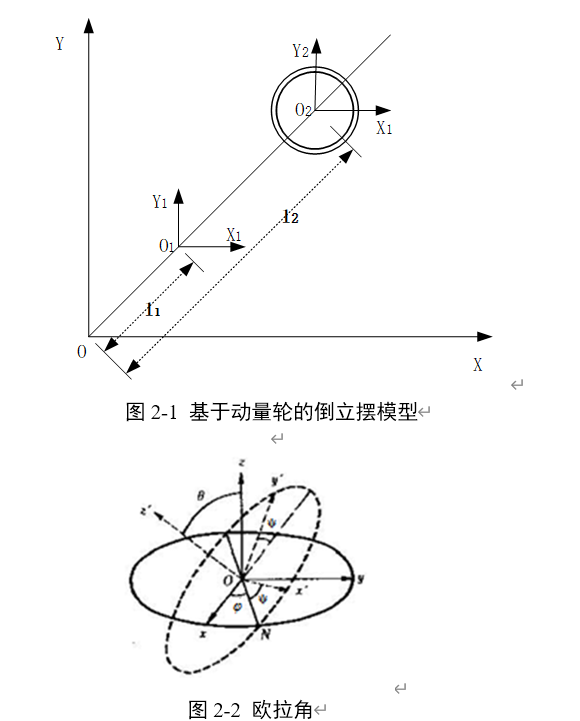
如图2-1所示,摆杆上端两反作用轮轮轴相互垂直且共同与杆垂直布置,分别由两固定于杆上的直流电机驱动。整个系统可以看做是由三个刚体组成的。摆杆(包括电机的外壳和定子部分)为刚体1,两反作用轮(包括电机的转子部分)为刚体2、3。刚体的质心到地面质点间的距离分别为l1、l2、l3。刚体质量分别为m1、m2、m3。刚体三个轴的转动惯量(坐标轴与惯性主轴重合)为I1x、I1y、I1z、I2x、I2y、I2z、I3x、I3y、I3z。采用欧拉角描述摆杆在静止坐标系中的姿态。如图2-2所示,o-xyz为静止坐标系,o-x_1’y_1’z_1’是固连在摆杆上的坐标系。章动θ、自转ψ、进动φ。整个系统运动部件的自由度是5(摆杆3个自由度、反作用轮各一个)。摆杆固连坐标系各轴角速度与欧拉角的关系为:反作用轮1转轴z_2’与摆杆坐标轴y_1’平行反向,相对电机定子或摆杆的转动角用α表示。相应角速度与摆杆角速度之间的关系为: 反作用轮2转轴z_3’与摆杆坐标轴x_1’平行反向,相对电机定子或摆杆的转动角用β表示。相应角速度与摆杆角速度之间的关系为:采用拉格朗日力学建立动力学方程组。系统拉格朗日函数其中T是系统的总动能,V是系统的总重力势能(注:以下角速度符号统一使用摆杆角速度代替,坐标轴所带角标均省略)。系统拉格朗日函数的广义坐标对应系统所有运动部件的自由度,因此L函数有五个广义坐标θ、ψ、φ、α、β。列出拉格朗日方程和广义坐标及其对应的广义力其中τ_1、τ_2是两轮的驱动力矩。将L函数代入拉格朗日方程,就可以得到系统的动力学方程组。由于涉及变量比较多,导致方程组表达式过于冗长、繁杂。为了便于分析,必须对其进行简化。如何简化才能对模型精度影响最小,保证可控性,又能使表达式更简洁?进行以下简单的定性分析:章动角θ和自转角ψ都是输出变量,不能省略。两轮转动角α和β是快速变化量,也不能省去。只有进动角φ是慢变量,对系统的动力学模型影响最小,且表达式中只有φ的一、二阶导(即进动角速度和加速度),因此省略后完全不用考虑进动角的变化。简化后得到方程组
由于省略了一个广义坐标,因此方程组中有一个方程是多余的。
采用直流电机驱动动量轮。直流电机的动力学简化模型
其中u和i分别是电机的实时驱动电压和电阻,Lm是电枢自感系数,Rm是电枢电阻,Ke是反电势系数,ω是电机的输出转速,kt是电机的输出转矩系数。由于自感系数Lm较小,因此略去自感项。
再将简化的方程 代入方程 的第四和五方程(用=替换≈),得到
将此方程代入方程组 的第一和三方程(用=替换≈),第二个方程被略去,得到
选择略去的第二个方程的原因会在后续的分析中给出。
2.2控制系统设计方案
2.2.1自抗扰控制原理
方程组表明这是一个二输入二输出的非线性耦合控制系统。自抗扰控制理论中有较为简便的处理非线性和解耦合的方法,因此选择ADRC作为此系统控 制算法的理论基础。(简要介绍...)自抗扰控制器结构如图2-3所示2.2.2系统解耦
根据ADRC理论中多输入多输出控制系统的表达形式将动力学方程改成
其中
称为系统的“动态耦合”部分,
称为“静态耦合”部分。引入“虚拟控制量”
于是多变量耦合的MIMO控制系统 变成了由控制量U分别以U1和U2分量分别作用于两个方程的解耦合系统。显然,解耦合成功的条件是控制矩阵B可逆。
求B的行列式,得
由此可得,只有当章动角θ=0(即摆杆完全竖直)时,才不可解耦。只要摆杆偏离竖直状态,就可以解耦控制。方程组 第二个方程无法化成显含控制量的形式, 不能满足解耦的条件,这就是略去它的原因。利用虚拟控制量U,耦合控制系统分解为了两个分别单独受控的两输入两输出系统。因此,可以分别对这两个控制回路(通道)设计自抗扰控制器。如图2-4所示
2.2.3 自抗扰控制控制器算法
自抗扰控制器一般由过度过程发生器、扩张状态观测器和状态误差反馈控制器等环节组成。其中扩张状态观测器是自抗扰理论中的核心。状态观测器是用来估计系统实时状态为状态反馈提供条件。而扩张状态观测器的作用除了估计状态(以二阶系统为例)的“位置”和“速度”之外,还要估计出状态受内外扰动获得的“加速度”,方程中的 和 。之所以要估计状态的“加速度”,正是因为被控对象建模不够精确,这种不精确就是所谓的“内扰”。利用扩张状态观测器来估计内外扰动,从而在控制量中添加相应的补偿项抵消扰动。
1)扩张状态观测器
一般的状态观测器要用到被控对象的模型信息,即中的

所以本文采用一中通用的不含被控对象模型信息的扩张状态观测器。
2)过渡过程发生器
在给控制系统输入阶跃信号时,系统响应通常会经历一个超调过程,有时甚至会伴随而来经久不息的震荡。给控制系统安排过度过程可以使阶跃信号变成渐变的信号,从而改善响应的动态品质。过度过程发生器通常也由非线性跟踪微分器构成。
3)误差反馈控制器
本文采用改进型的被称为“非线性PID”的误差反馈控制器。其中非线性体现在采用了非线性跟踪微分器的结构对输出量的微分信号进行提取。
这种非线性跟踪微分器具有低通滤波的功能,能够抑制输出信号中的噪声,同时又能以最小的相位滞后代价跟踪输出信号的导数。由非线性跟踪微分器构成的PID控制器克服了传统PID控制器的快速性与超调小相矛盾的固有缺陷。
2.2.4 自抗扰控制器参数整定
根据自抗扰设计的分离性原理,分别对自抗扰控 制器TD、ESO和NLSEF三个模块进行独立设计。基 于以上模块在设计上的独立性,综合采用经验试凑法 和带宽法对每个模块参数单独整定,再综合调整[23]。1) 微分跟踪器
在跟踪微分器中需要整定h、r0、h0,采用经验试凑法整定参数。h与采样时间有关,根据立方体机器人的电器硬件处理速度,采用50 ms采样及处理周期可以满足控制要求,取h = 0.05;微分跟踪器的跟踪速度r0影响系统的跟踪精度和过渡过程时间,r0过大会使过渡过程太短,跟踪信号无限逼近输入信号,r0过小则过渡过程较长,影响系统的响应速度,通常取r0 = 0.000 1/h2;增大的滤波因子h0可提高滤波效果,但同时会使跟踪信号的相位滞后,通常取h0 = 20h。2) 扩张状态观测器
在扩张状态观测器中,需要整定参数δ、β01、β02、β03。δ为函数fal( )在原点附件的线性区间宽度,δ过小容易出现原点附近的高频震颤,δ过大会减弱ESO 对非线性信号的逼近能力,一般取δ = 0.01。 ESO是自抗扰控制技术的最关键、最核心模块,参数β01、β02、β03的整定效果决定自抗扰控制器的控制性能[24]。根据文献[25]提出的基于带宽的参数整定方法,将控制器参数转换为带宽的函数,根据观测器带宽ωo,给定β01、β02、β03的整定值满足β01 = 3ωo, β02 = 3ωo2 , β03 = ωo3。通过选择合理的观测器带宽ωo,可同时确定反馈增益参数,有效减少了调节参数的数量。3) 非线性误差反馈.
在非线性误差反馈中,需要整定c、r、h1、b01。根据积分步长,阻尼系数c = 0.5,控制量增益r满足 r = c/hα, α = 1.5 − 0.5sign(1 − h)。精度因子h1取值越小,控制精度越高,但过小会引起系统抖振现象。根据阻尼系数c,精度因子取值满足h1 = ch。第3章 硬件系统设计
3.1机械结构的设计
3.1.1电机的选择
由分析可知,因为控制周期T_c=10 ms,所以要求电机的电气常数τ≤1 ms,同时,由分析结果可以得到,电机可能在调节的初期发生过载,所以要求电机有一定的瞬时过载能力,综上,我们选用一款领新电气的无刷直流电机,电机的外观如图3-1(a),电气参数如图4-1(b)。该电机功率50W,机械时间常数12ms,电气常数0.3ms,满足要求,并且具有32.4mNm/A的转矩输出。
图3-1(b)
图3-1 (a)电机实物图;(b)电机数据图
3.1.2结构设计
使用Solidworks三维CAD软件设计,包括摆杆、动量轮和连接支架等。图3-2、图3-3分别是设计效果图和实物图。3.2硬件设计
3.2.1设计总览
本设计的主控芯片采用STM32F103,主要由主控模块、无刷直流电机驱动、Gyro模块、功能开关、BOOST电路及BUCK电路构成。整体硬件设计框图如图3-4所示。电机驱动和控制电路分别由BOOST模块和BUCK模块提供动力,其中继电器的作用是为了保护驱动电路,当电源开关打开时,系统先使控制电路达到稳定状态,再通过软件开关使得继电器闭合,给驱动电路提供动力;同时当驱动器过流时会给芯片一个中断,使得继电器断开,从而达到保护驱动电路的目的。无刷电机是通过主控芯片发出的6路PWM波控制的;霍尔信号不仅可以提供换相信号,也可以用于计算电机的转速。Gyro模块是检测Cubli的Roll角和GyroRoll,为自抗扰控制提供必要的信息。上位机通讯是将系统的实时状态发送给计算机,作为监测和记录。功能开关为用户提供不同的功能选项。3.2.2 各个功能模块的具体结构和作用
1.主控模块是控制电路的核心,采用的是STM32F104VET6核心板,实物如图3-5所示。整个系统的主要控制任务包括无刷电机的控制、Cubot的控制、Gyro信息的读取和处理、上位机信息的交互等。其中最占用资源的是无刷电机的控制,因为电机的电气时间常数较低,所以PWM的载波频率随之提高,随之而来的计算频率增高,并且无刷直流电机的控制需要6路PWM波,所以综上所述使用STM32F103系列芯片,又因为整个控制需要GPIO个数较多,所以使用F103系列中的VET6型号,该芯片拥有72MHz的主频,2个ADC,可以采集电压和电流信号,硬件PWM电路,和霍尔异或电路,为电机的控制提供了充分的便利。
2.控制电路
主控制电路主要由五个部分组成,分别是核心板电路、按键输入电路、过流调节电路、继电器控制电路、电机端电压滤波电路。A.核心板电路(如图3-6)
共有72GPIO端口,已用24个,包括:6路PWM输出端口、3路外部中断端口、三路电流采样端口(PS:只做监测使用)、三路端电压采样端口(监测使用)、陀螺仪通讯端口和上位机通讯端口、三个霍尔信号输入端口以及驱动电路控制端口。
B.按键输入电路(如图3-7)
总共三个常开按钮,按钮PIN_1接入3.3V电压,PIN4接入主控芯片相应的外部中断引脚,当按下按钮,芯片引脚为高电平,触发上升沿中断。
C. 过流调节电路
该电路输出是OC_ADJ信号,是电机驱动电路的输入,通过调节分压阻的大小,得到不同的过流信号。
D.继电器控制电路(如图3-8)
RELAY引脚接STM32GPIO,当RELAY为低,三极管工作在截止区域,当RELAY为高,三极管工作在饱和区,该电路的目的是控制继电器的关断。二极管起到续流作用
E.电机端电压滤波电路(如图3-9)
该电路作为上位机调试用,因为电机的端电压是一个PWM波,所以为了或者可读的端电压数值,需要对其进行滤波,并且截止频率ω_c=k∙2πf_c,k<1,f_c为PWM载波频率。
3.无刷直流电机驱动
电机驱动器的目的是了将直流电压逆变成交流电压,驱动电机旋转。该驱动使用DRV8602驱动芯片驱动6个MOS管,MOS管的型号是NCE82H110D(V_DS=82V,I_D=110A,R_DS(ON) <7mΩ)。
主要包括逆变电路、驱动芯片电路、驱动芯片稳压电路、电流采样电路及端电压电压跟随电路。该电路并不具备通讯能力,这也就意味着,驱动电机所需要的控制算法、PWM信号都必须由主控芯片输出。
4.陀螺仪模块
实物如图3-14 所示
该模块采用MPU9250,并结合Cortex-M0内核处理器,利用卡尔曼滤波融合算法,解算出实时稳定的姿态角。与主控芯片通讯频率为200Hz,能够满足控制要求。
5.电源驱动模块
Boost模块可以将锂电池11.1V的电压转换成24V的驱动电压,并且拥有60W的最大输出功率,保证了电机的正常运行,Buck模块将锂电池电压转换成稳定的5V电压,为控制电路提供高品质的输入功率。如图3-15 所示
3.3 系统总成
动量轮采用3D打印加工而成,摆杆采用铝合金加工而成,其整体图如3-16所示:第4章 软件系统设计及分析
4.1软件描述部分
软件部分主要包括主控芯片接受MPU9250发送的姿态信息的串口中断服务程序,电机速度反馈信号处理程序和控制算法程序等三个部分。主程序包含串口、定时器、延时、PWM输出函数的初始化。
4.1.1电机速度反馈信号处理程序
电机的反馈信号是一系列的的高低电平,经过示波器检测得到高电平的时长是电机旋转一周的十分之一。当电机匀速运行时,反馈信号时序如图4-2所示使用stm32的定时器输入捕获功能,对测量反馈信号的一个高电平时间即可获得此高电平时间段内的电机转速。分别使用定时器TIM2和定时器TIM5来测量电机1和电机2的速度反馈信号。在电机速度角快时,输入捕获中断正常进入和结束,当电机速度太小时,受到控制周期的限制,中断时间不能持续太长,应该显示在一个控制周期内。所以,通过反馈信号获取的速度值存在一个下限,小于这个值就测量不到了。4.1.2陀螺仪姿态数据处理程序
陀螺仪的数据是通过和陀螺仪模块串口通讯得到,因为陀螺仪向单片机发送数据的频率是200Hz,为了保证信息的连续性和完整性,需要赋予该串口通讯最高优先级。数据以数据帧的形式传输,每一种数据一帧包含11个字节,帧头占两个字节,第一个0x55是帧头标志字节,第二个0xXX区分信息类兴型。以下是角度和角速度的数据帧格式。此控制系统只需用到姿态角和姿态角变化速率两个信息。陀螺仪需要发送的信息类型已经在上位机中设置好了。角速度数据帧格式:
0x55 0x52 wxL wxH wyL wyH wzL wzH TL TH SUM
计算方法:
wx=((wxH<<8)|wxL)/32768*2000(°/s)
wy=((wyH<<8)|wyL)/32768*2000(°/s)
wz=((wzH<<8)|wzL)/32768*2000(°/s)
校验和:
Sum=0x55+0x52+wxH+wxL+wyH+wyL+wzH+wzL+TH+TL
角度数据帧格式:
0x55 0x53 RollL RollH PitchL PitchH YawL YawH TL TH SUM
计算方法:
滚转角(x 轴)Roll=((RollH<<8)|RollL)/32768180(°)
俯仰角(y 轴)Pitch=((PitchH<<8)|PitchL)/32768180(°)
偏航角(z 轴)Yaw=((YawH<<8)|YawL)/32768*180(°)
校验和:
Sum=0x55+0x53+RollH+RollL+PitchH+PitchL+YawH+YawL+TH+TL
4.2实验装置测试及结果分析
4.2.1单轴平衡试验
为了验证算法和电路结构,预先搭建了一个验证平台,平台包括一个3D打印的动量轮单摆结构、电机驱动以及STM32开发板,见图4-3。该平台实现了单摆的平衡。4.2.2陀螺仪数据传输与姿态换算
根据陀螺仪的串口通信协议,按照需求接收陀螺仪发送过来的角速度与角度数据。原始数据是由是一个一字节的十六进制数组成的数据帧组成的。通过转换成浮点数得到角速度和欧拉角的实际值。欧拉角需要再一次转化才能变成需要的姿态数值。如图4-4所示是主控芯片打印到串口助手上的摆杆实时姿态。Theta1表示摆杆偏转方向是绕动量轮1的轴,逆时针方向正,顺时针方向负。Theta2表示摆杆偏转方向是绕动量轮2的轴,逆时针方向正,顺时针方向负。4.2.3动量轮速度的测量
根据电机反馈信号的高电平的宽度可以算出电机转动一周的时间,进而得到电机的转速。利用STM32 定时器的输入捕获功能可以测得反馈信号的电平的宽度。图4-4是测得电机转速打印到串口助手的数值。第5章 总结
本作品是对多输入输出非线性强耦合控制系统的一次实践探索,实现了一个具有较高鲁棒性的双轴动量轮倒立摆大角度回正并自平衡。在着手进行实物设计之前做了大量的分析,得到单闭环PID无法校正系统的理论依据,针对系统的多输入多输出耦合的特性采用自抗扰控制。通过引入ADRC中的虚拟控制量的方法来解耦合,通过扩张状态观测器来估计内外扰动量的大小。动态性能以及对输入能量的控制方面都比前者更优秀,同时为了提高有限输入情况下系统的鲁棒性。仿真和实验结果证明了混合控制系统具有良好的鲁棒性。
在理论层面:从建立动力学模型到设计控制器都考虑了系统的非线性和耦合效应。并且在控制器的选择上也有针对性的考察了控制器对非线性和解耦合系统的控制性能。实践层面:实现了陀螺仪与主控芯片的通信,成功获取摆杆的姿态数据并转化成所需的坐标变量。通过对电机反馈信号的处理得到电机的瞬时速度。这些都是实施控制算法的基础。由于所选电机在启动、换向上速度突变的特性,使得摆杆的平衡效果不如预期。在以后的实践中加强理论与实践的学习。
参考文献
[1] 王贤明, 陈炜, 赵新华. 倒立摆系统起摆与稳摆控制算法研究综述[J]. 自动化技术与应用, 2015, 34(11): 5-9.
[2] 陈志刚, 阮晓钢, 李元. 立方体机器人自抗扰平衡控制方法[J]. 控制与决策, 2019, 34(06): 1203-1210.
[3] Türkmen A, Korkut M Y, Erdem M, et al. Design, implementation and control of dual axis self-balancing inverted pendulum using reaction wheels[C]2017 10th International Conference on Electrical and Electronics Engineering (ELECO). IEEE, 2017: 717-721.
[4] 王德爽. 基于自抗扰算法的导弹制导系统设计研究[D]. 哈尔滨工程大学, 2012.
[5] 叶镭, 夏元清, 付梦印, 李春明. 无人炮塔炮控系统自抗扰控制[J]. 控制理论与应用, 2014, 31(11): 1580-1588.
[6] Gao Z. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the American control conference. 2006, 6: 4989-4996.
[7] 王俊伟, 于新海, 温荣, 白春梅, 肖晓. 倒立摆状态观测器的输出反馈控制器研究[J]. 机床与液压, 2021, 49(08): 152-155.
[8] 李臻, 刘龙龙, 宋战胜, 宋正河, 朱忠祥. 基于动量飞轮的单轴倒立摆系统实验装置[J]. 实验室研究与探索, 2021, 40(04): 75-78+91.
[9] 韩京清. 从PID技术到“自抗扰控制”技术[J].控制工程, 2002(03): 13-18.
[10] 韩京清. 自抗扰控制技术[J]. 前沿科学, 2007(01): 24-31.
[11] 张荣, 韩京清. 串联型扩张状态观测器构成的自抗扰控制器[J]. 控制与决策,2000(01): 122-124.
[12] Olivares M, Albertos P. Linear control of the flywheel inverted pendulum[J]. ISA transactions, 2014, 53(5): 1396-1403.
更多研电赛作品请查看2021年研电赛获奖作品合集