摘要:本文将由浅入深的介绍永磁同步电机转动的控制方法,涵盖的内容包括位置开环控制——让电机转动起来,有传感器和无传感器的位置闭环控制,永磁同步电机的数学模型——电机规格书上各个参数的含义,部分现代控制理论——观测器设计和控制器参数配置,以及弱磁控制,高频注入等其他方向。
1.直流电机
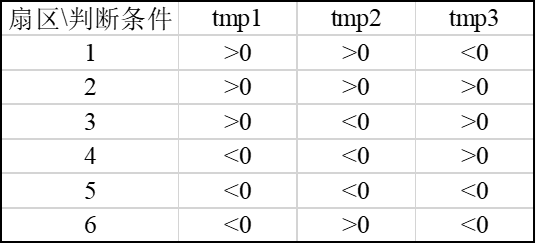
首先复习一下直流电机,直流电机的转子由线圈组成,定子由永磁体组成。根据麦克斯韦理论,线圈通电后会产生磁场,成为另一个磁体。当线圈处于如图1.1所示位置时,根据朴素的生活经验——“同性相斥、异性相吸",此时磁铁会发生转动;当线圈转到处于如图1.2所示位置时,线圈磁场和永磁体磁场正交时,此时线圈不受磁场力的作用,理论上线圈可于此位置处静止;而当线圈转到处于如图1.3所示位置时,线圈磁场和永磁体磁场相吸时,如果没有电刷这项伟大的发明的话,线圈将不再转动,电刷此时会自动使线圈电流反相,从而改变线圈磁场方向,使电机重新处于图1.1的状态,直流电机转动情况如图2所示。 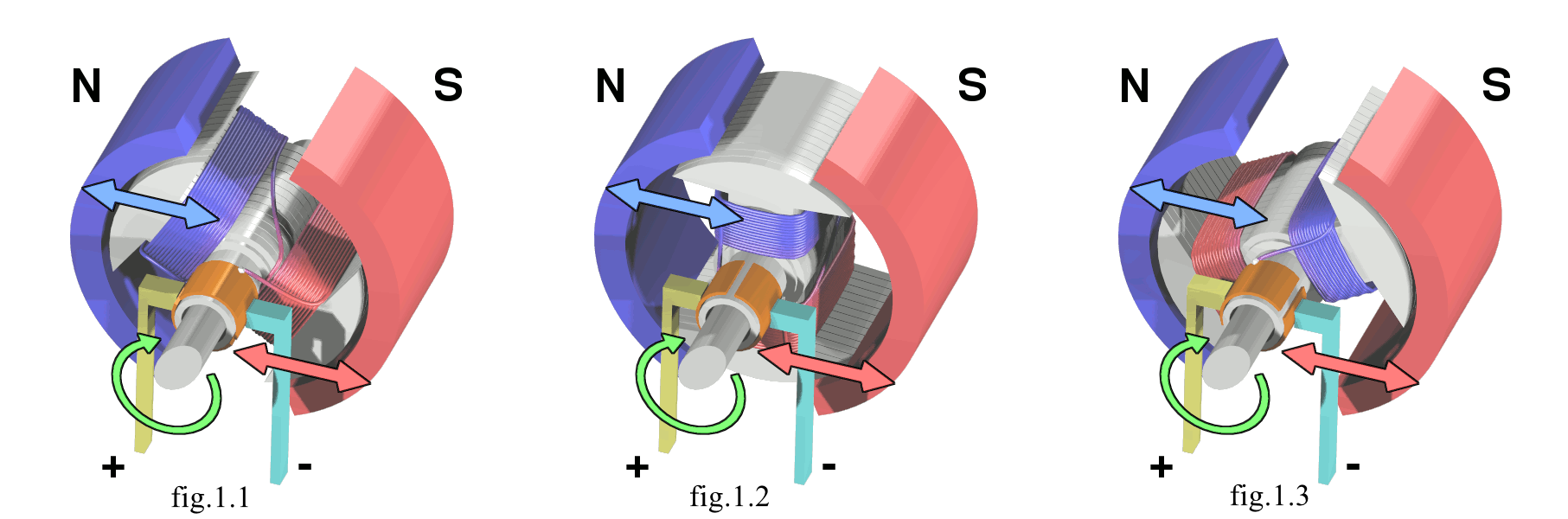
电刷极大简化了直流电机的控制——只要通以母线直流电压,直流电机就可以直接转动,但是在电刷进行线圈电流换相时,部分绕组直接短路于母线电压之下,损害了直流电机的寿命。 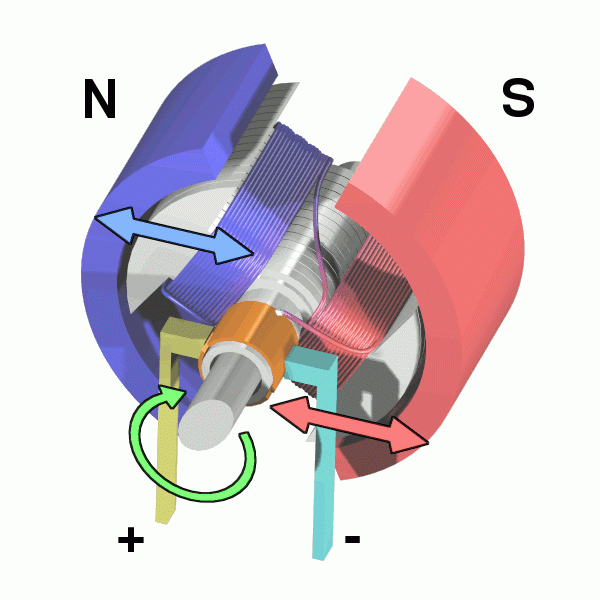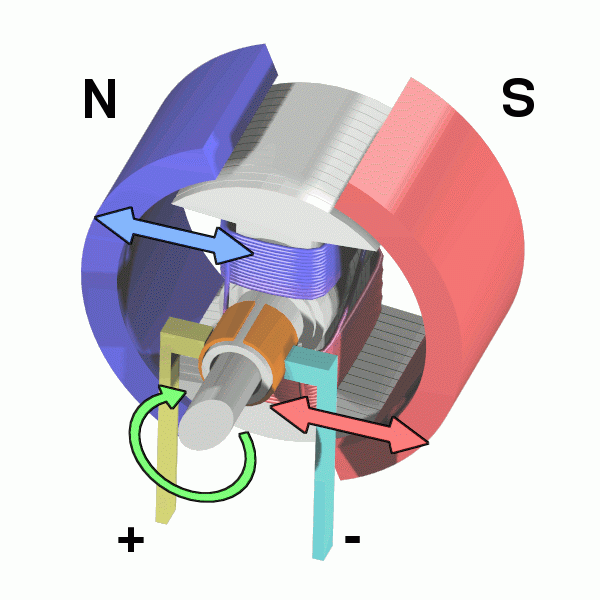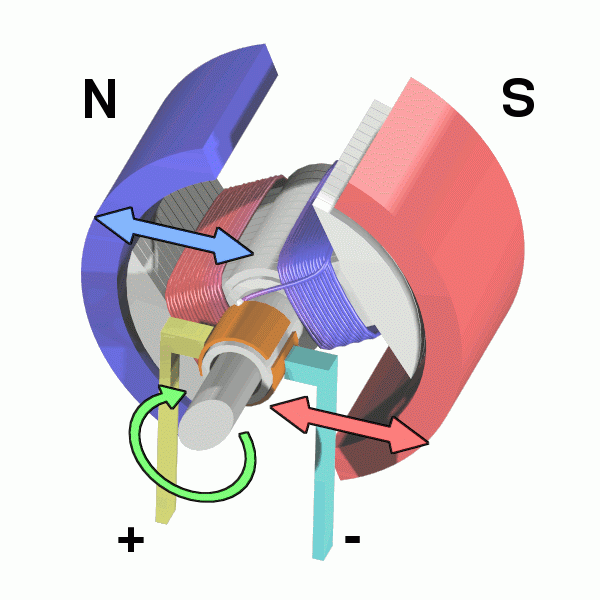
根据直流电机的原理和弊端,人们就开始思考:"永磁体磁场难以控制,而线圈的磁场可以通过改变电流的方式任意控制",因而"永磁体作为转子,线圈作为定子"的永磁同步电机应运而生,如图3所示。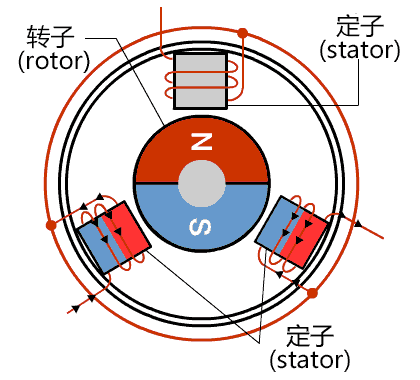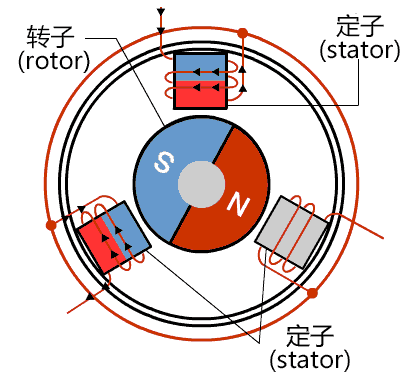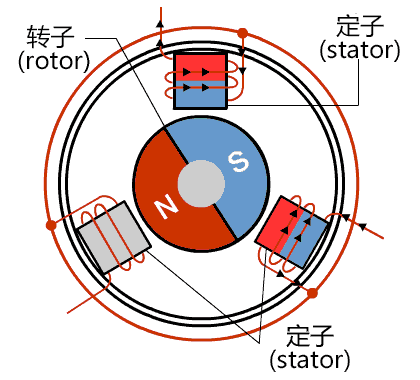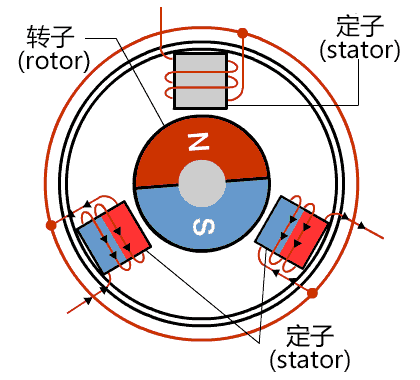
永磁同步电机又被称为无刷直流电机,为了使永磁体不断转动,线圈必须产生旋转的磁场,正负极性不断切换才能和永磁体一直处于相斥的状态,因此虽然永磁同步电机的母线电压是直流电压,但是其线圈上的电流却是交流的,永磁同步电机实际上是一种交流电机。
2.电流反馈与坐标变换
阅读过以上内容,想必大家对永磁同步电机已经有了直观的感受,下面的内容会涉及一些数学推导。
根据麦克斯韦方程,可以知道电流是产生磁场的真正激励。现在永磁同步电机具有三相绕组,自然而然可得到三相静止坐标系,定子相电流ia、ib、ic是三相定子相电流,考虑到三相定子电流为矢量,三相定子电流为幅值相等,时间相位上相差了120°,同时三相绕组在三相静止坐标系中空间相位上也相差了120°。同时考虑时间和空间上的相位差,三相定子电流矢量的合成如图6所示。 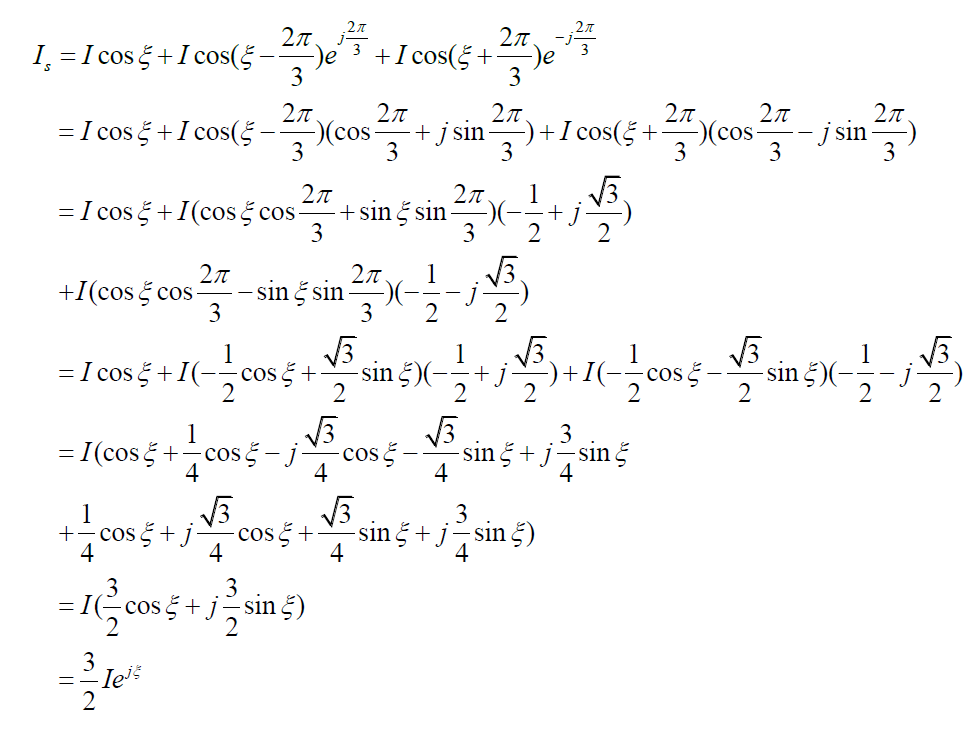
为便于计算和使用方便,现将相差120°的三相静止坐标系转化为相差90°的两相静止坐标系,此变换被称为clark变换,将三相定子电流ia、ib、ic向两相静止坐标系投影(alpha,beta)可得ialpha,ibeta。同时由图6可见三相合成的矢量大小是三相静止坐标系下相电流矢量大小的3/2倍,为保证等值变换,则需要在变换矩阵中乘以2/3这个系数。 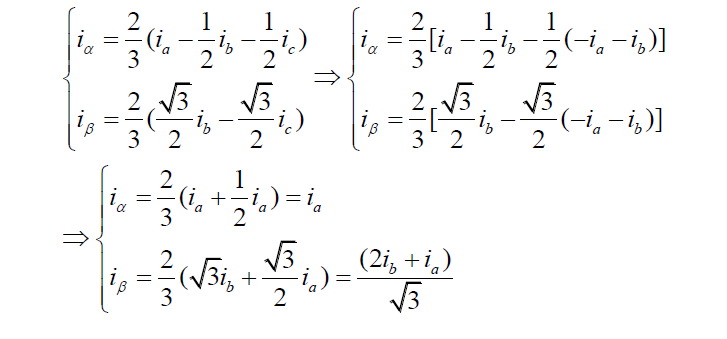
clark变换只是数学上的一个把戏,而引出park变换则需要一点技巧,引用TI的例子:请思考如何用摄像机拍摄旋转木马上的小女孩? 
答案是把摄像机也架设在旋转木马上。
请记住永磁同步电机中的电流矢量是空间和时间维度上的概念。因而将两相静止坐标系变换为两相同步旋转坐标系,其中d轴为永磁体转子磁场方向,q轴为垂直于永磁体转子磁场方向。 

经过一系列坐标变换,定子电流矢量由三相静止坐标系下复杂的表达式,变为同步旋转坐标系下的简洁表达式,可以表达为id、iq、theta这三个标量的形式,d轴电流产生磁通,q轴电流产生旋转力矩,因此通过给定固定大小的q轴电流和一个随时间变换的角度theta就可以得到随时间变化的三相定子电流的空间矢量,使永磁体转子随三相定子电流产生的旋转磁场转动起来。
3.SVPWM与标幺值
实际应用中,通常无法直接给定三相定子电流,只能通过给定相应的电压激励产生所需电流,三相逆变器实现了由直流母线电压到三相交流定子电流的转换,如图11所示。 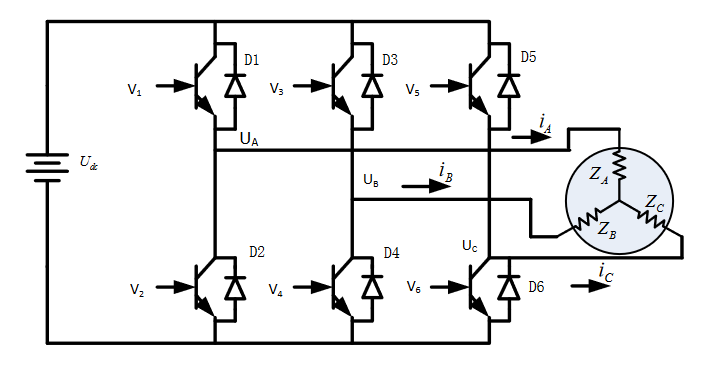
忽略永磁同步电机中耦合项的影响,可认为d轴电压产生磁通,q轴电压产生旋转力矩,给定Vd=0、固定Vq和随时间变化的角度theta,即可产生永磁体转子旋转的力矩。通过park逆变换和clark逆变换,可实现由同步旋转坐标系到三相静止坐标系的变换,产生所需的VAN、VBN、VCN三相定子电压。 
由逆变换可知,所需的VAN、VBN、VCN三相定子电压幅值随时间变化呈正弦波,而通过SVPWM调制可使六个电力电子开关工作于特别开关切换顺序,在定子上生成类似正弦的电流。
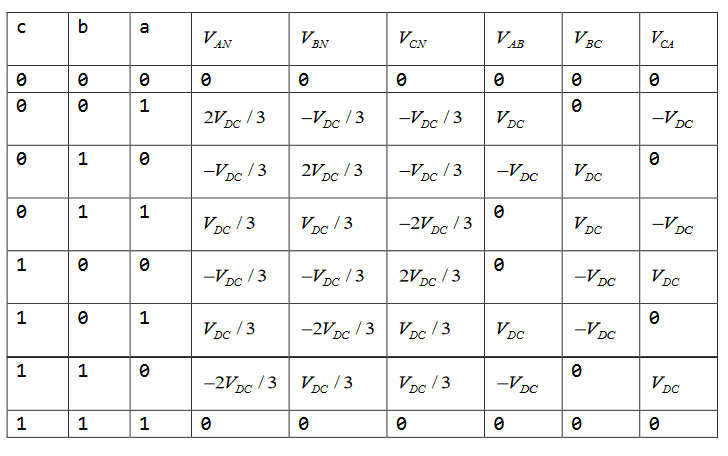
下面考虑如何用三相逆变器生成所需电压,假设电机三相阻抗相等为Z,接入直流母线电压后共有"一相进两相出"和"两相进一相出"两种情况,其中并联的两相绕组阻抗为Z/2。若上桥臂开关管导通记为“1”,关断记为“0”,并且每相上桥臂开关管开关状态以c、b、a排列,电机接入直流母线电压为“一相进两相出”的情况有(0,0,1)、(0,1,0)、(1,0,0)。接入直流母线电压为“两相进一相出”的情况有(0,1,1)、(1,0,1)、(1,1,0),另外电机未接入直流母线电压的情况有(1,1,1)和(0,0,0)。不同开关组合状态下对应三相逆变器的相电压和线电压如表1所示。 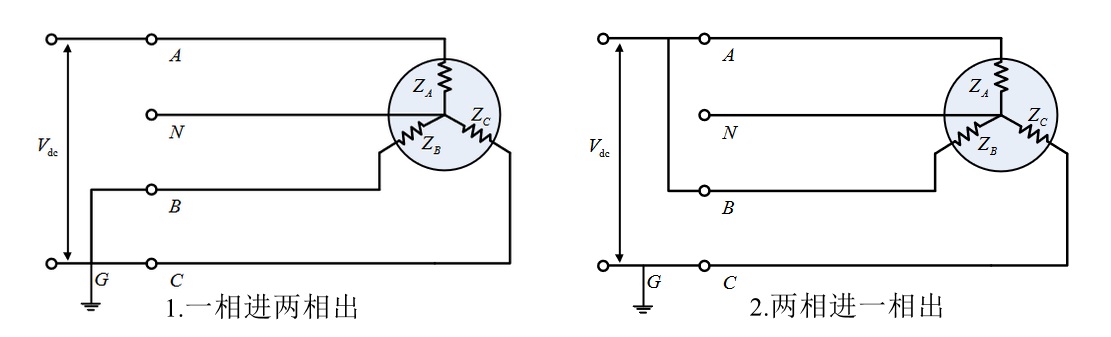
再复习一下,clark变换是幅值、频率完全等效的数学变换,其合成矢量完全一致,只是相位由原来相差120°的三相静止坐标系变成了相差90°的两相静止坐标系。不同开关组合状态下对应三相逆变器在两相静止坐标系下电压如表2所示。 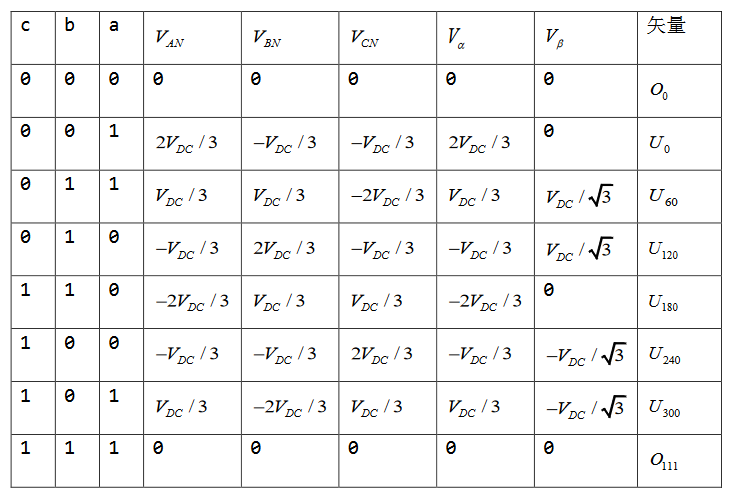
容易得到两相静止坐标系下电压幅值同样为2/3Vdc,并借助相对于alpha轴的夹角命名六个非零电压空间矢量和两个零矢量,六个非零矢量按照三相逆变器不同开关状态分布,相邻之间夹角为60°,两个零矢量位于原边处,如图14所示。 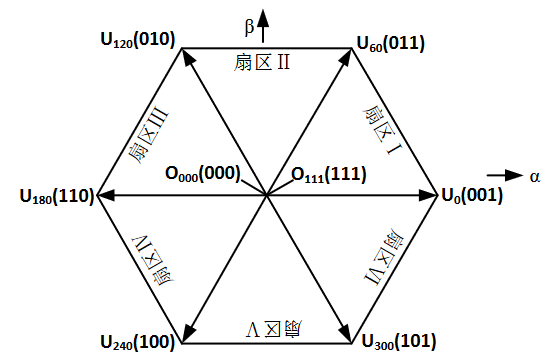
为方便分析,现进行标幺值定义。根据线圈的星型连接方式,容易得到线电压幅值即母线电压为Vdc,相电压为Vdc/sqrt(3),以相电压为基准,各基本空间矢量电压2/3Vdc为2/sqrt(3)。
由于非零矢量的基本电压矢量只有6个,因此只能形成一个正六边形的磁链轨迹。为获得近似圆形的磁链轨迹,可以利用这几个非零的基本电压空间矢量的线性时间组合来合成所需的电压矢量,同时插入零矢量进行调整。以位于扇区1的电压矢量Vref为例, 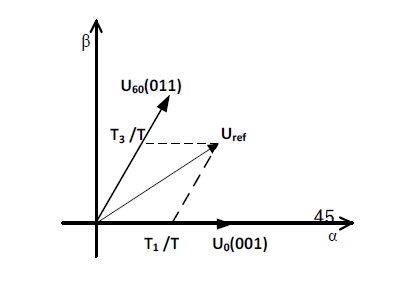
图15中有两组矢量基,分别是两相静止坐标系(alpha,beta)和扇区1中的基本空间矢量(U0,U60)。其中两相静止坐标系下的值是控制电机所需的电压矢量,可用扇区1内的基本空间矢量来表示,如图16所示: 
由图16所示公式,可以计算出基本空间矢量的作用时间,全部使用标幺值计算,先算出T3,然后把T3代入可以算出T1,周期T内剩余时间为零矢量作用时间: 
其他扇区的基本空间矢量的作用时间,可由相同原理得出。
在确定了基本空间矢量的作用时间后,本着开关切换次数最少的原则,在两个非零基本空间矢量作用之间插入零矢量,从而确定基本空间矢量作用的先后次序。
基本空间矢量的排列顺序为:以零矢量O(000)开始,然后是只含有一个"1"的U0(001),U120(010),U240(100),然后是含有两个"1"的U60(011),U180(110),U300(101),最后作用的是另外一个零矢量O(111),这是上半个PWM周期的基本空间矢量的作用次序。
由于采用对称的PWM调制方法,在下半个PWM周期中,以零矢量O(111)开始,然后然是含有两个"1"的U60(011),U180(110),U300(101),然后是只含有一个"1"的U0(001),U120(010),U240(100),最后作用的是另外一个零矢量O(000)。
然后根据基本空间矢量的作用时间,规定零矢量作用时间为T0,只含有一个"1"的基本空间矢量作用时间为T1,含有两个"1"的基本空间矢量作用时间为T2,从而确定不同桥臂的PWM波形的占空比。 
a. 只含有一个"1"的基本空间矢量作用开始的时刻即零矢量O(000)结束的时刻为taon;
b.含有两个"1"的基本空间矢量作用开始的时刻为tbon;
c.零矢量O(111)作用开始的时刻为tcon; 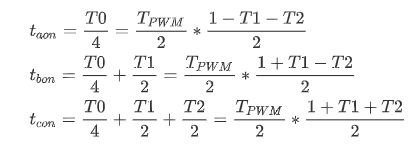
以第一扇区为例,可得到逆变器三相PWM波形如图19所示: 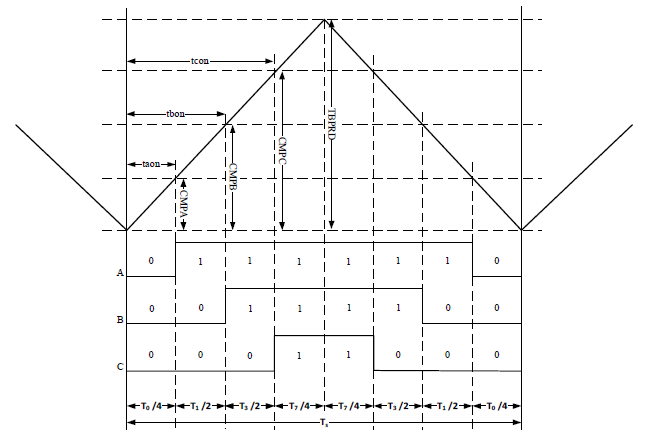
由图19可知,已知基本空间矢量作用时间后,为得到三相桥臂的各相占空比,需确定目标矢量所在扇区,根据两相静止坐标系下的电压矢量值关系进行判断,其实就是图20所示的三条直线的线性规划问题: 
4.总结
到这里为止,已经构建了从理论到作用于电机的实际电压矢量的桥梁,终于可以实现本章开始的目标,让电机转动起来(位置开环控制)。
给定ud=0,uq=常量,转子位置theta按恒定速度递增,使线圈产生一个恒定的磁场,经park反变换到两相静止坐标系,得到ualpha和ubeta,然后经SVPWM调制作用于三相逆变桥,电机转子即可转动起来。
由于此时转子位置theta由外部任意给定,并不是转子真正的位置,因而称为位置开环控制,电机转动耗费电流较大,转换效率较低,需要调整合适的uq电压常量和给定的恒定速度,才能实现电机较为平稳的转动。
在下一章中,将介绍利用外部磁传感器获取转子真正位置后,如何实现电机转子的定向磁场控制(FOC)。
更多电机控制技术干货请关注电机控制技术专栏。扫描下方二维码加入电机控制技术交流群与作者交流,如二维码失效请添加极术小姐姐微信(id:aijishu20),备注电机控制,加入微信群。