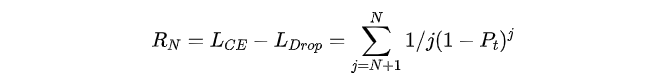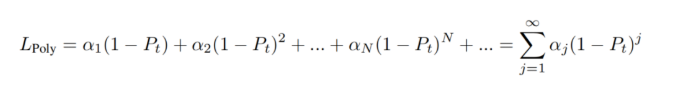Cross-entropy loss和Focal loss是在训练深度神经网络进行分类问题时最常见的选择。然而,一般来说,一个好的损失函数可以采取更灵活的形式,并且应该为不同的任务和数据集量身定制。通过泰勒展开来逼近函数,作者提出了一个简单的框架,称为
PolyLoss,将损失函数看作和设计为多项式函数的线性组合。PolyLoss可以让Polynomial bases(多项式基)的重要性很容易地根据目标任务和数据集进行调整,同时也可以将上述Cross-entropy loss和Focal loss作为PolyLoss的特殊情况。大量的实验结果表明,在
PolyLoss内的最优选择确实依赖于任务和数据集。只需引入一个额外的超参数和添加一行代码,PolyLoss在二维图像分类、实例分割、目标检测和三维目标检测任务上都明显优于Cross-entropy loss和Focal loss。
1、简介
原则上,损失函数可以是将预测和标签映射到任何(可微)函数。但是,由于损失函数具有庞大的设计空间,导致设计一个良好的损失函数通常是具有挑战性的,而在不同的工作任务和数据集上设计一个通用的损失函数更是具挑战性。
例如,L1/L2 Loss通常用于回归的任务,但很少用于分类任务;对于不平衡的目标检测数据集,Focal loss通常用于缓解Cross-entropy loss的过拟合问题,但它并不能始终应用到其他任务。近年来,许多研究也通过元学习、集成或合成不同的损失来探索新的损失函数。
在本文中,作者提出了PolyLoss:一个新的框架来理解和设计损失函数。
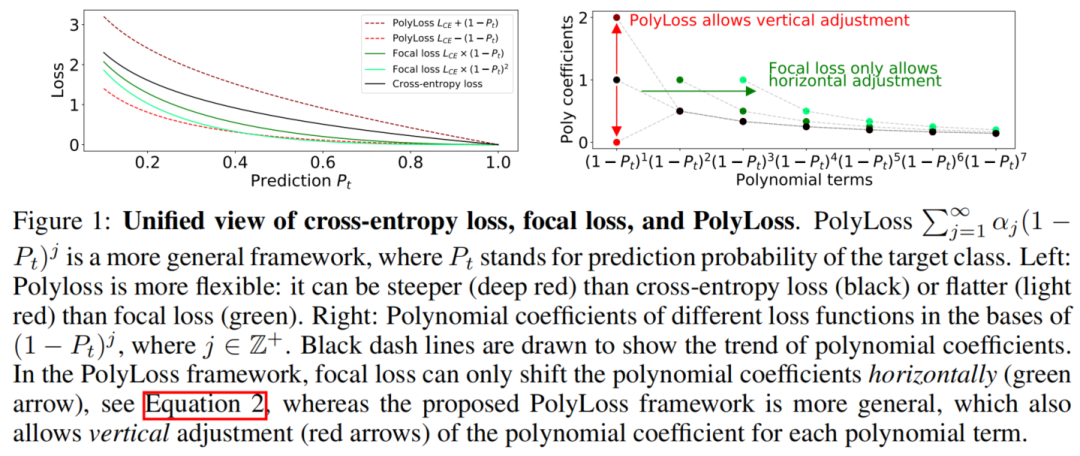
作者认为可以将常用的分类损失函数,如Cross-entropy loss和Focal loss,分解为一系列加权多项式基。
它们可以被分解为的形式,其中为多项式系数,为目标类标签的预测概率。每个多项式基由相应的多项式系数进行加权,这使PolyLoss能够很容易地调整不同的多项式基。
- 当时,
PolyLoss等价于常用的Cross-entropy loss,但这个系数分配可能不是最优的。
研究表明,为了获得更好的结果,在不同的任务和数据集需要调整多项式系数。由于不可能调整无穷多个的,于是作者便探索具有小自由度的各种策略。作者实验观察到,只需调整单多项式系数,这里表为示,足以实现比Cross-entropy loss和Focal loss的更好的性能。
2、主要贡献
图1
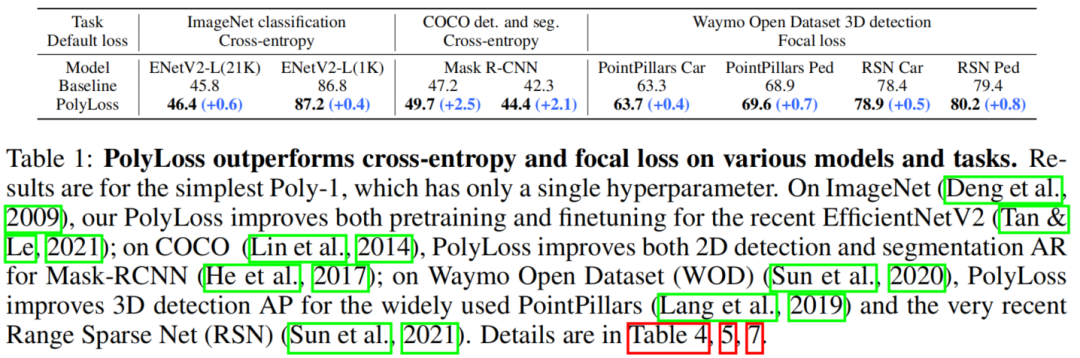
Insights on common losses:提出了一个统一的损失函数框架,名为PolyLoss,以重新思考和重新设计损失函数。这个框架有助于将Cross-entropy loss和Focal loss解释为多损失族的2种特殊情况(通过水平移动多项式系数),这是以前没有被认识到的。这方面的发现促使研究垂直调整多项式系数的新损失函数,如图1所示。New loss formulation:评估了垂直移动多项式的不同方法,以简化超参数搜索空间。提出了一个简单而有效的Poly-1损失,它只引入了一个超参数和一行代码。New findings:作者发现Focal loss虽然对许多检测任务有效,但对于不平衡的ImageNet-21K并不是很优秀。作者还发现多项式在训练过程中对梯度有很大的贡献,其系数与预测置信度相关。Extensive experiments:在不同的任务、模型和数据集上评估了PolyLoss。结果显示PolyLoss持续提高了所有方面的性能。
3、PolyLoss
3.1 Cross-entropy loss as PolyLoss
3.2 Focal loss as PolyLoss
3.3 与回归和一般形式的联系
4、理解多项式系数的影响
在前面的谈论中建立了PolyLoss框架,并展示了Cross-entropy loss和Focal loss简单地对应于不同的多项式系数,其中Focal loss就可以表达为水平移动了多项式系数的Cross-entropy loss。
这里要深入研究了垂直调整多项式系数对于训练可能的影响。具体来说,作者探索了3种分配多项式系数的不同策略:
- 去掉高阶项
- 调整多个靠前多项式系数
- 调整第1个多项式系数
作者发现,调整第1个多项式系数(Poly-1)便可以最大的增益,而且仅仅需要很小的代码更改和超参数调整。
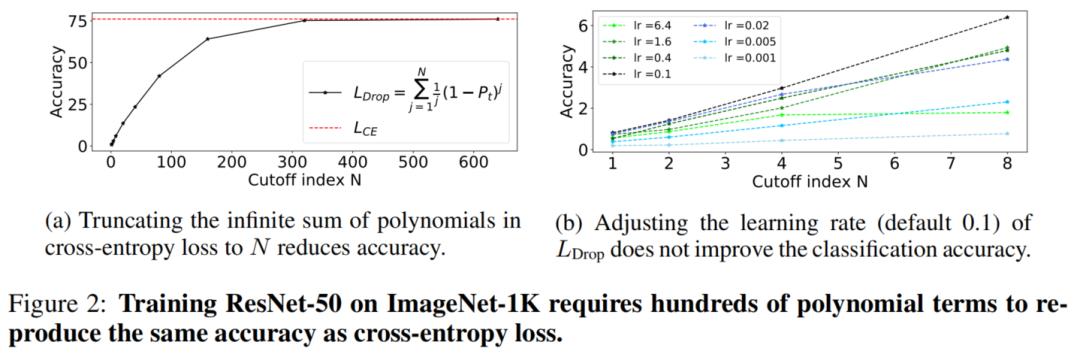
4.1 :回顾高阶多项式项的删除
已有研究表明,降低高阶多项式和调整前置多项式可以提高模型的鲁棒性和性能。作者采用相同的损失公式
Cross-entropy loss的性能。
如图2a所示,需要求和超过600个多项式项才能匹配Cross-entropy loss的精度。值得注意的是,去除高阶多项式不能简单地解释为调整学习率。为了验证这一点,图2b比较了在不同的截止条件下不同学习率下的性能:无论从初始值0.1增加或减少学习率,准确率都会变差。
为了理解为什么高阶项很重要,作者对Cross-entropy loss中去除前N个多项式项后的结果进行了求和:
定理1:
4.2 :扰动重要的多项式系数
在本文中提出了在PolyLoss框架中设计一个新的损失函数的替代方法,其中调整了每个多项式的系数。一般来说,有无穷多个多项式系数需要调节。因此,对最一般损失进行优化是不可行的:
第4.1小节已经表明,在训练中需要数百个多项式来很好地完成诸如ImageNet-1K分类等任务。如果天真地将方程中的无限和截断到前几百项,那么对这么多多项式的调优系数仍然会带来一个非常大的搜索空间。此外,综合调整许多系数也不会优于Cross-entropy loss。
为了解决这一问题,作者提出扰动交叉熵损失中的重要的多项式系数(前N项),同时保持其余部分不变。将所提出的损失公式表示为,其中N表示将被调整的重要系数(前N项)的数量。
4.3 :简单而有效
注意,所有训练超参数都针对Cross-entropy loss进行了优化。即便如此,对Poly-1公式中的第1个多项式系数进行简单的网格搜索可以显著提高分类精度。作者还发现对LPoly-1的其他超参数进行优化还可以获得更高的精度。
4.4 PolyLoss的Tensorflow实现
(1)、PolyLoss-CE
`def poly1_cross_entropy(logits, labels, epsilon=1.0):
# pt, CE, and Poly1 have shape [batch].
pt = tf.reduce_sum(labels * tf.nn.softmax(logits), axis=-1)
CE = tf.nn.softmax_cross_entropy_with_logits(labels, logits)
Poly1 = CE + epsilon * (1 - pt)
return Poly1
`
(2)、PolyLoss-Focal Loss
`def poly1_focal_loss(logits, labels, epsilon=1.0, gamma=2.0):
# p, pt, FL, and Poly1 have shape [batch, num of classes].
p = tf.math.sigmoid(logits)
pt = labels p + (1 - labels) (1 - p)
FL = focal_loss(pt, gamma)
Poly1 = FL + epsilon * tf.math.pow(1 - pt, gamma + 1)
return Poly1
`
5、实验
5.1 图像分类
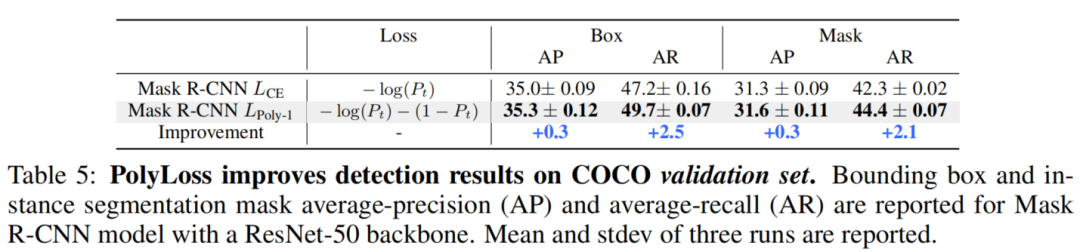
5.2 目标检测
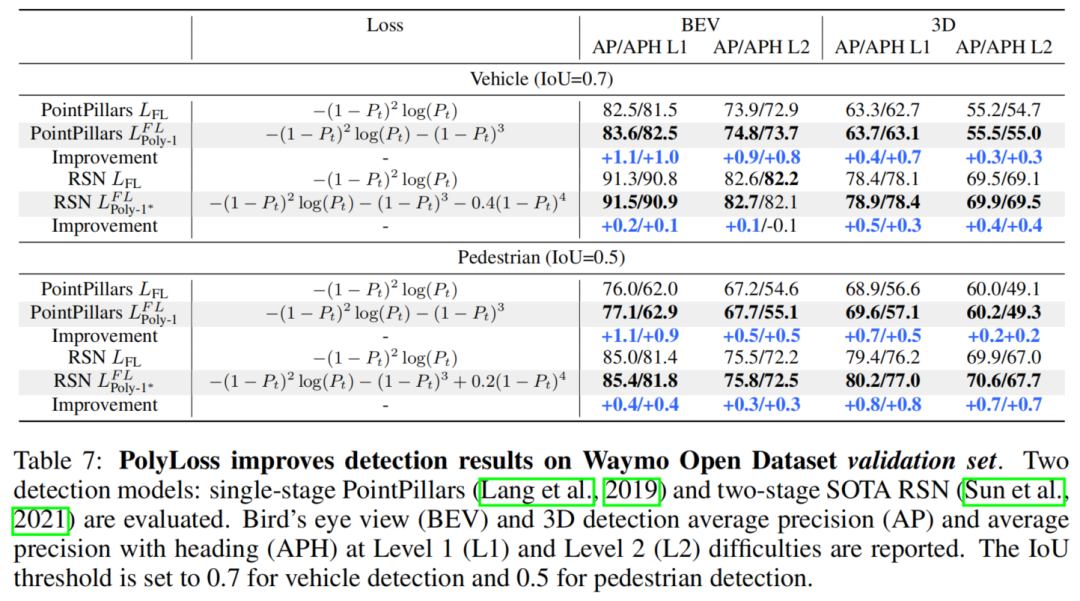
5.3 3D目标检测
原文:集智书童
推荐阅读