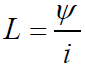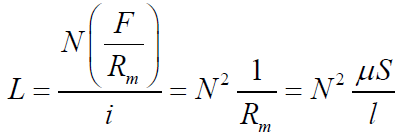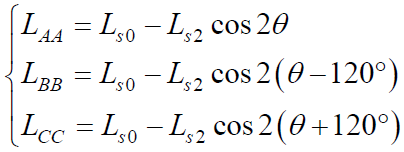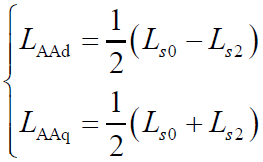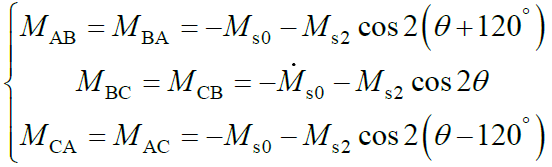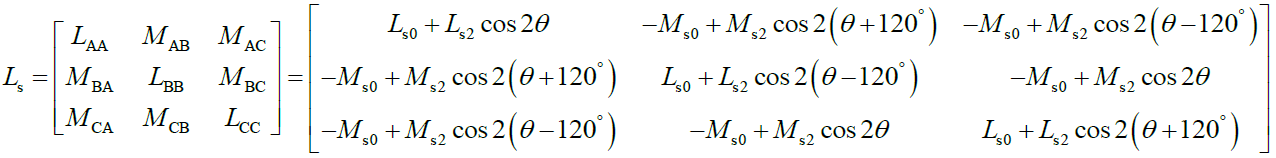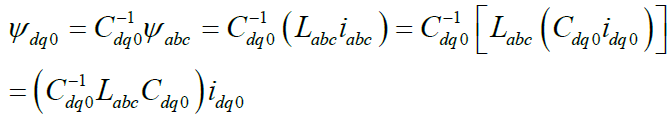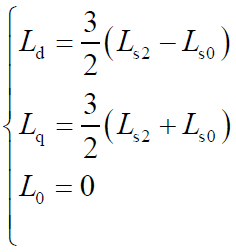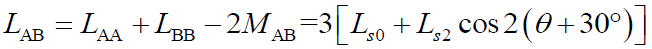作者:heguojia
来自:西莫电机论坛
1 dq电感的计算
电感是电机控制中的重要问题。电机控制中主要关注的是电机的dq轴电感。本节介绍dq轴电感的计算。
电感是衡量线圈电磁感应能力的物理量。我们用_ψ_表示磁链,_i_表示电流,则电感_L_可以表示为
(1)
上面是电感的定义式,用来定量分析的时候并不是很直观。所以,下面给出了电感的计算公式,表示了电感和磁路中各个物理量的关系。电感的计算公式为
(2)
式中,_l_为气隙长度,N为匝数,S为绕组的截面积,_μ_为磁导率。
在普通电感中,以上几个参数均为常数,因此电感是个恒定值(在不饱和的情况下)。在电机中,这种情况会有所不同。
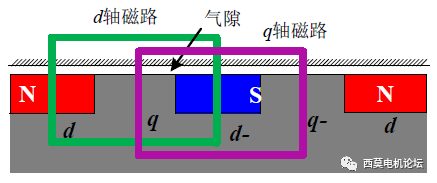
图1 内置式永磁同步电机磁路示意图
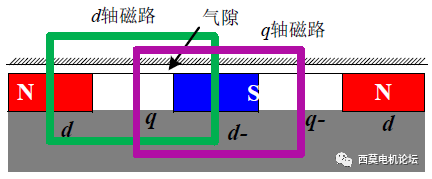
图1为内置式永磁同步电机的磁路示意图。由图可知d轴磁路由气隙、永磁体、铁芯组成。而q轴磁路由气隙和铁芯组成。在铁芯没有饱和的情况下,我们可以将铁芯的磁导率看作无穷大,此时磁路的磁阻取决于气隙和永磁体。在图1中很容易可以看出,d轴磁路的磁阻明显大于q轴磁路的磁阻,因此q轴电感要大于d轴电感。在内置式永磁同步电机中,由于转子在旋转过程中,永磁体和相轴线的相对位置发生变化,磁路一直在发生变化,因此等效磁阻,或者说等效磁导率是周期性变化的,这样导致电感的周期性变化。而在表贴式电机中,由于气隙磁导率处处相等,因此磁导率是一直保持不变的。如图2所示。关于dq轴电相对大小的问题,我们有了初步的结论。
图2 表贴式永磁同步电机磁路示意图
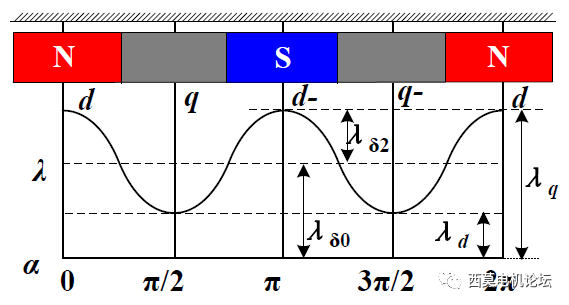
前面提到,内置式电机随着电机转子转动,磁路等效磁导率规律性变化,则定子绕组的自感和互感也会规律性变化。如图3所示为定转子的相对位置,在一个电角度周期之内,磁路变化了两个周期,根据公式,电感也会变化两个周期。因此,即电角度周期是电感变化周期的两倍。将图3中的磁导率变化曲线总结为公式。
(3)
式中,_α_为以_d_轴为原点时,某点距d轴的电角度。
图3 气隙磁导示意图
因此,对于内置式永磁同步电机,三相绕组的自感分别为
(4)
对于表贴式电机,由于气隙均匀,则其自感为
(5)
式中,_L_s0和_L_s2分别为自感_L_AA、_L_BB、_L_CC中的恒定分量和二次谐波的幅值;_θ_为电角度。
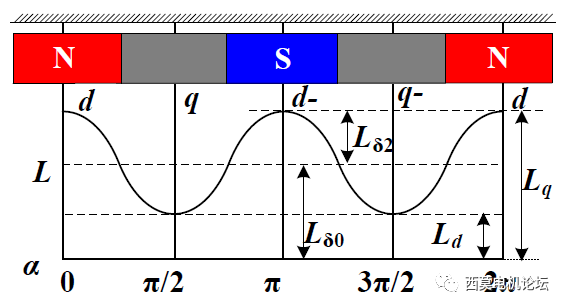
图4 电感曲线示意图
其实,细心的读者从图4中也可以看出,d轴的电感是电感曲线的谷值,q轴电感是电感曲线的峰值。但是,我们还没有考虑互感,所以还没有办法过早下结论,等我们在最后总结。
以BC相绕组之间的互感_M_CB为例。根据互感定义,_M_CB表示单位B相电流产生的基波磁场与C相绕组中所形成的互感磁链为
(6)
式中_L_AAd和_L_AAq是A相绕组轴线与直轴和交轴重合时,与通过气隙进入转子这部分磁链相应的电感。由图3可知
(7)
则相应的互感为
(8)
在忽略漏感的情况下
(9)
同样的,_M_s0为恒定分量,_L_s0为二次分量幅值。
所以,由于漏感很小,因此对于理想电机,可以认为
(10)
其余的相间互感可以表示为
(11)
对于表贴式电机,其相间互感
(12)
通过以上步骤,我们得到了三相电感的自感和互感的表达式。但是为了得到dq电感,我们还需要对三相电感进行变换。
从上面的分析中我们可以看出,相电感的表达式中含有2_θ_的周期性分量。我们可以通过dq0变换把时变的定子电感矩阵对角线化和常数化。将电感矩阵写为
(13)
在确定了图中的电感矩阵之后,我们有两条路线去得到dq0电感。
(1)磁链方程
首先,我们已经知道Park变换矩阵及其逆矩阵为
(14)
那么,求解磁链矩阵时,有
(15)
因此,可以得到
(16)
(2)求对角矩阵
这是一种更直接的方法。但是物理意义并不是很容易看出来。对于电感矩阵,我们如果想得到dq0电感矩阵,需要求其特征值。
令,则
(17)
解以上方程可以得到三个特征根。
(18)
在前面我们提到,
(10)
因此,
(19)
如果根据特征值进一步推导可以发现,把电感矩阵对角化的两个变换矩阵就是dq0变换的矩阵及其逆矩阵。
综合来看,我们可以知道,在电感曲线中q轴电感为电感曲线最大值1.5倍,d轴电感为电感曲线最小值的1.5倍。
其实,大家更关心的问题是,怎样通过外部测量来知道dq轴电感。对于电机控制来说,只需要知道dq轴电感多大就可以建立电机的数学模型。所以一种快速简单估算dq电感的方法是很重要的。根据前面的推导,我们已经知道了dq轴电感与一相自感的关系。但是,在接不到中性点的情况下,我们没有办法直接测相电感。在这种情况下,我们可以通过ABC三端中的两端来间接获取单相电感。
图5 电感测量电路
如图5为测量电感的电路,我们以AB相之间为例。我们现在已经知道A相自感、B相自感、AB相互感的表达式。因此,根据电感串联规则可以算出AB之间的电感为
(20)
根据上面的公式可知
(21)
当然,我们可能知道不容易获得特定的转子角度,但是,通过使用LCR表测量_L_AB的变化曲线即可以根据_L_AB的最大值和最小值,我们可以得到dq电感的估计值。
2 电感的饱和
电机控制环路的参数,弱磁控制的给定值都与电感大小有关。如果在电机运行中发生电感饱和现象,电机控制的效果和性能将受到很大的影响。在上一节的推导过程中,我们假设磁路仅受转子旋转时位置变化导致的等效磁阻变化影响。因此,算得的dq轴电感是恒定值。但是,这一结论的前提为电机是理想电机,没有铁芯饱和。在电机工作在大转矩或者弱磁区中时,定子电流较大,往往使电机铁芯发生饱和的情况。本节简单分析dq轴电流变化对dq轴电感的影响。
根据上一节提到的电感的计算公式我们知道,电机定子绕组的匝数,截面积等参数是不变的。电感大小主要受磁路中的磁导率影响。
(2)
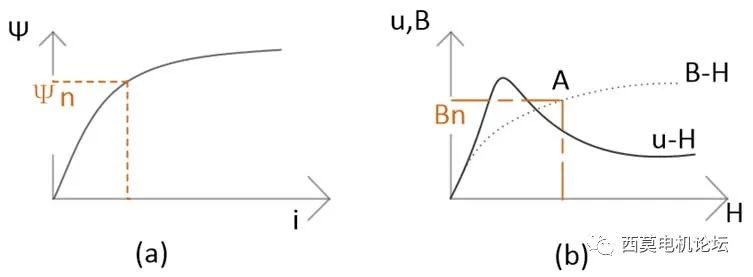
在电机的磁路中,有铁芯、气隙、永磁体三种材料。其中,气隙和永磁体的磁导率很小,磁阻很大,可以看作是恒定值。但是铁芯存在饱和的现象。如图6所示为铁芯的磁导率曲线示意图,当电流增大时,磁动势增大,但是由于铁芯的磁导率进入饱和区后会变小,产生的磁链与磁动势不成比例,因此,电感会减小。
图6 铁芯磁导率曲线示意图
具体到永磁同步电机,由于工况变化,电流矢量会影响铁芯饱和,从而影响绕组电感的大小。但是,电流矢量又分解为dq轴电流,因此,dq轴电流针对铁芯饱和情况的影响又各不相同。
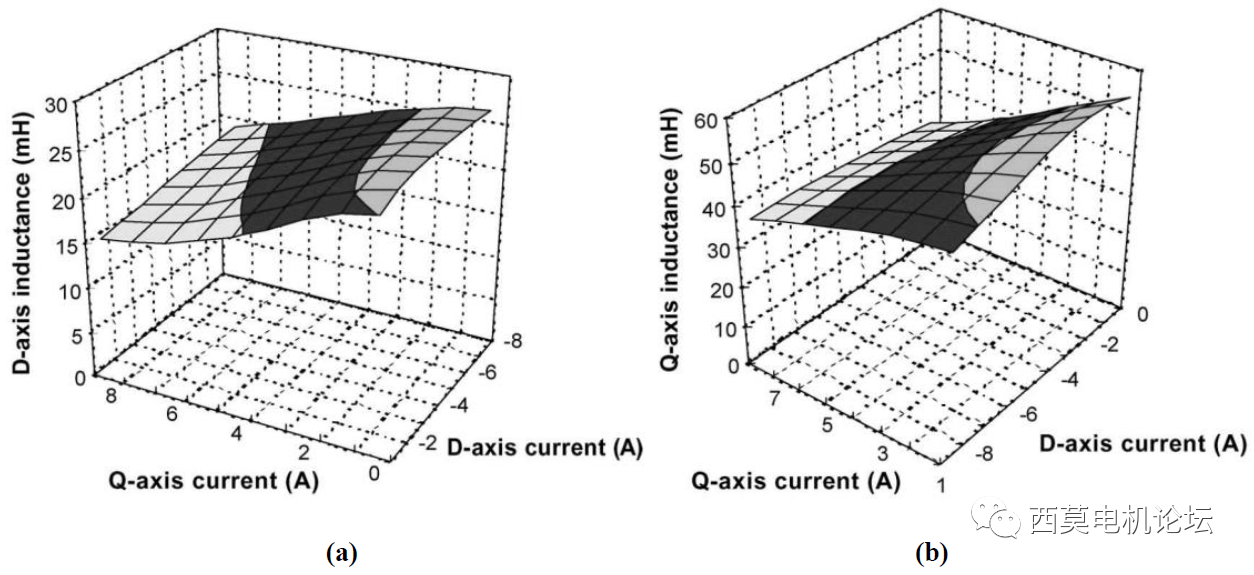
对于q轴,当电机输出转矩增大的时候,由于q轴电流增大,所以q轴磁路中出现饱和,q轴电感相应减小。
对于d轴,当电机工作在弱磁状态时,d轴电流向反方向增加,d轴磁路处于弱磁状态。此时,由于d轴磁链被削弱,因此,d轴电感是增大的。但是,由于d轴磁路的磁阻比q轴大,因此,在相同的电流幅值作用下,d轴电感的变化比q轴的要更小。
图7 dq电感随电流变化示意图
如图7为dq电感随电流变化的示意图。从图8(a)可以看出,在d轴电流反向增大时,d轴电感增大。从图8(b)可以看出,在q轴电流增大时,q轴电感减小。
3 总结
电感是电机中的重要参数,涉及内容非常复杂。但本文没有只是从电机控制的角度去简单理解永磁同步电机中dq电感的计算和变化特性。相信对于快速评估dq轴电感有重要的作用。dq轴电感的实际情况更为复杂,比如,dq轴之间还存在交叉饱和效应、电感的漏感以及电感的高次谐波问题,都会对控制产生影响。但是,限于笔者的水平和时间,这篇文章仅展示了电感的冰山一角。
参考文献:
- [1] 汤蕴璆, 交流电机动态分析. 交流电机动态分析,2005.
- [2] G. Qi, J. T.Chen, Z. Q. Zhu, D. Howe, L. B. Zhou and C. L. Gu, Influence of Skew andCross-Coupling on Flux-Weakening Performance of Permanent-Magnet Brushless ACMachines, IEEE Transactions on Magnetics, 2009, (45)5: 2110–2117.
- [3] 王艾萌, 新能源汽车新型电机的设计及弱磁控制[M]. 新能源汽车新型电机的设计及弱磁控制, 2014.
- [4] L. Chedot andG. Friedrich, A cross saturation model for interior permanent magnet synchronousmachine. Application to a starter-generator [C], Industry ApplicationsConference, 2004: 64–70.
- [5] X. Liang, A.M. El-Serafi and S. O. Faried, Application of the Finite-Element Method for theDetermination of the Parameters Representing the Cross-Magnetizing in SaturatedSynchronous Machine [J], IEEE Transactions on Energy Conversion, 2010, 8(3):333-342.