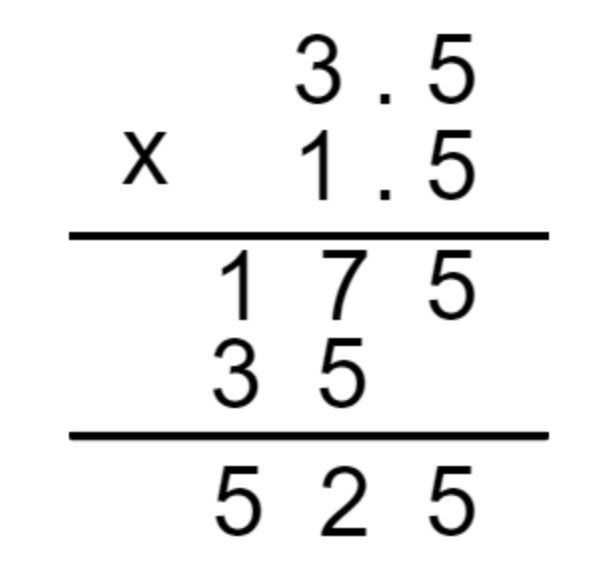1. 前言
linux 内核有一套对系统负载的衡量算法,其底层使用的是指数衰退算法。
指数衰退算法从逻辑上是必须要依赖小数运算的,然而如你所知,内核中不允许使用浮点运算,硬浮点会引入 FPU,这将导致内核态-用户态之间切换时,需要保存更多的浮点寄存器而引入额外的开销,而软浮点依赖编译器实现的软浮点运算子,亦是额外的开销。
本文的出发点即在此,从工程角度分析 linux 内核负载计算所涉及到的技巧细节。这个分析是有普适价值的,可以借鉴到读者自己的内核态编程中,同时也适用于其他需要高效进行小数计算的场景。
本文基于 4.9 内核。
2. 指数衰退
本章节介绍指数衰退算法,已经熟悉了的同学直接跳过。
2.1 是什么
假设有这样一组系统的负载采样时序:
我们希望衡量系统这段时间内的负载情况,要求将过去时间点上的负载采样也纳入对系统整体负载的影响考量。
一个最容易想到的算法就是取 Tn-5 - Tn 这段时间内的负载均值,作为系统负载的量化。
一定时间内负载采样点取均值,该思想的本质是过去一段时间内,任意采样点上的值,对当前系统负载的评估的影响有相同权重。
指数衰退的思想,本质上是不同时间点上的采样的对整体评估的影响权重不同,离当前时刻越近的采样点影响权重越高,反之越小,并且采样点间的影响权重呈指数级衰退。该思想也常用于对曲线的滤波平滑(指数平滑)。
2.2 数学推导
假设当前时刻采样对整体评估的影响权重是 w,写成公式(1):
L = w \* Ln + (1 - w) \* w \* Ln-1 + (1 - w)2 \* w \* Ln-2 \+ (1 - w)3 \* w \* Ln-3 + (1 - w)4 \* w \* Ln-4 \+ (1 - w)5 \* w \* Ln-5 \+ ...记上一次采样点上系统的整体负载为 L',得 式(2):
L' = w \* Ln-1 + (1 - w) \* w \* Ln-2 + (1 - w)2 \* w \* Ln-3 \+ (1 - w)3 \* w \* Ln-4 + (1 - w)4 \* w \* Ln-5 \+ ...式(2) 两边乘上 (1 - w),得 式(3):
(1 - w ) \* L' = (1 - w) \* w \* Ln-1 + (1 - w)2 \* w \* Ln-2 + (1 - w)3 \* w \* Ln-3 \+ (1 - w)4 \* w \* Ln-4 + (1 - w)5 \* w \* Ln-5 \+ ...式(3) 代入 式(1),得 式(4):
L = w \* Ln + (1 - w ) \* L' 2.3 工程化
对于式(4):
w:当前采样值对整体负载评估的贡献权重
Ln:当前采样值
L':上个采样点上,系统的整体负载评估值
L:当前采样点上,系统的整体负载评估值
写成代码:
/* curr 是当前采样值
* last_load 是上一时刻的系统负载
*/
double cal_load(double last_load, unsigned long long curr)
{
// 0.6 只是随意取的一个权重值
static double w = 0.6;
return w * curr + (1 - w) * last_load;
}
int main() {
int i;
double load;
unsigned long long samplings[] = {
[0] = 9,
[1] = 8,
[2] = 7,
[3] = 6,
[4] = 5,
[5] = 7,
[6] = 6,
[7] = 4,
[8] = 2,
[9] = 1,
};
for (i = 0; i < sizeof(samplings) / sizeof(unsigned long long); ++i) {
load = cal_load(load, samplings[i]);
printf("%lf\n", load);
}
}
输出:
5.400000
6.960000
6.984000
6.393600
5.557440
6.422976
6.169190
4.867676
3.147070
1.8588283. 浮点数
3.1 浮点数的存储
有关此话题更为严谨的讨论,参考 《IEEE Standard 754Floating Point Numbers》Steve Hollasch 一文。
对浮点数在计算机的存储很懂的同学直接跳过本节。
如你所知,单精度(float)、双精度(double)数在计算机中的存储,是遵循 IEEE 标准的。这个很好理解,因为计算只认识 0 和 1,无论什么数存到内存之后就是一坨 01 序列。如果不制定标准,计算机就不知道该怎么解释这串 01 序列。
本节以单精度的表示来讲解(双精度原理一样,只是阶码、尾数所占的比特位数与单精度不同)。
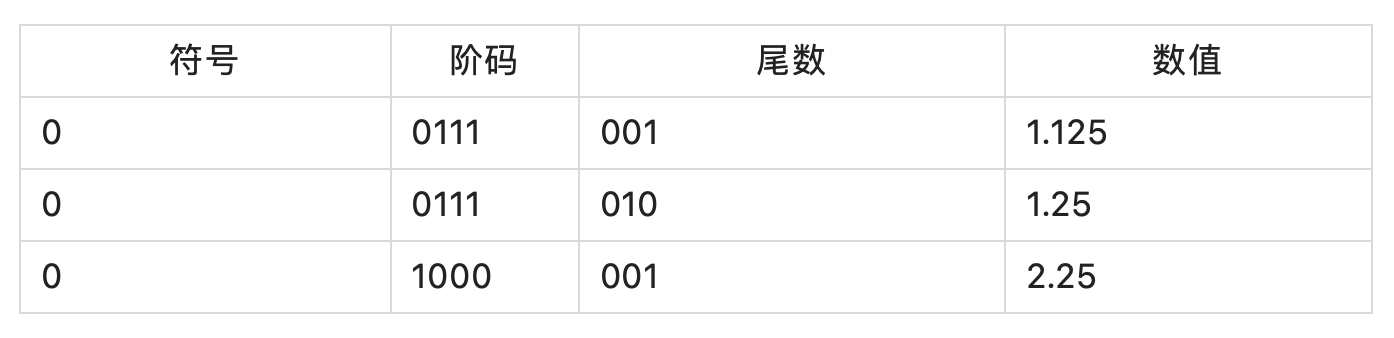
单精度在计算机中如此表示:
此单精度浮点数(下文简称“浮点数”)的值为 式(5):
V = (-1)S x (1.M) x 2(E - 127)
这里对 式(5) 稍微解释一下:
- 阶码理解为指数,尾数理解为底数。
- 为什么当尾数存储的是 M 时,实际的运算使用的尾数却是 1.M?
因为这里本质上是科学计数法,科学计数法要求底数的整数部分不能为 0:
1000 = 1 x 103 这是正确的表示法
1000 = 0.1 x 104 这是错误的表示法在浮点数的存储中亦然,计算机使用二进制,故尾数的整数部分必然是 1,既然必然是 1,这个 1 也就没有必要存储了,如此尾数位中可以节省一个 bit 来表示更高精度的数据。
- 为什么当阶码存储的是 E 时,实际的运算使用的阶码却是 E - 127?
阶码是可能存在为负数的情况的:
0.001 = 1 x 10\-3浮点数亦不例外。试想:
- 如果 E 为 8 个 1(0xFF),也就是 255,那么此时算出来的实际阶码为 255 - 127 = 128
- 如果 E 为 8 个 0(0x00),也就是 0,那么此时算出来的实际阶码为 0 - 127 = -127
换句话说,我们在这里加上 127 这个偏置,效果就是用 127 来表示逻辑上的 0,那么:
- 逻辑上的 +128,表示为 127 + 128 = 255
- 逻辑上的 -127,表示为 127 - 127 = 0
通过使用 127 来表示逻辑 0 这个 trick,实现了用 8 位位宽表示逻辑上的 [-127, 128]。
3.2 进制转换
为了方便后面定点数的推导,本章节提一下十进制与二进制间的转换算法。
已经很懂的同学自行跳过。
- 十进制整数转二进制
算法:除 2 取余,逆序输出。
算法比较简单,这里直接用 python 代码描述(挫):
def dec_int2bin(n):
res = ""
while n:
res = str(n & 1) + res
n /= 2
print res
# 打印十进制数 12 的二进制表示
dec_int2bin(12)
# output
# 1100- 十进制小数转二进制
这里注意十进制的小数转二进制,算法与十进制整数不同。
算法:将小数部分不断乘以2,每次取整数部分,直到最后乘积结果为 1。
用 python 描述(挫):
def dec_frac2bin(n):
res = "0."
nbits = 0
while n:
n *= 2
INT = int(n)
n = n - INT
if nbits % 4 == 0 and nbits:
res += " "
nbits += 1
res += str(INT)
print res
# 打印 0.3125 的二进制表示
dec_frac2bin(0.3125)
# output
# 0.0101计算过程:
- 二进制小数转十进制
算法:各个位乘以 2 的负次方,最后将结果相加(本质上就是十进制小数转二进制的逆运算)。
如二进制的小数 0.0101,转成十进制小数:
0 x 2\-1 + 1 x 2\-2 + 0 x 2\-3 + 1 x 2\-4 \= 0.3125用 python 描述(挫):
def bin2dec(n, w):
res = 0
n = int(n * pow(10, w))
while n:
res += pow(2, -w) if n % 10 == 1 else 0
w -= 1
n /= 10
print res
# 打印二进制小数 0.0101 的十进制数值
bin2dec(0.0101, 4)
# output
# 0.31253.3 实践验证理论
根据上两节的知识,我们来验证一下实际的浮点表示是否符合预期:
void main(void) {
float f = 12.3125;
assert(sizeof(f) == sizeof(uint32_t));
printf("0x%x\n", *(uint32_t *)&f);
}上面的代码打印出 12.3125 在内存中存储的二进制 bit 序列,直接以图的形式展示输出结果:
- S:0,表示是正数
- E:0x82 - 127 = 3
- M:1.1000 101(b) = 1.5390625(d)
根据 式(5):
V = 1.5390625 \* 23 = 12.31253.4 “浮”的本质
随着尾数、阶码的变化,小数点在最终数值中的位置是跟着变化的,换句话说,你根本不知道它小数点后是精确到第几位的。
3.5 精度的丧失
注意:本节的推导皆是通过工程手段进行的,没有严谨的数学论证,因为我不会。
浮点的“点”虽然是在“浮”的,但限于计算机的离散性,无法无限精度的“浮”
浮点数精度的丧失从两个角度来考虑,我们观察 3.2 节提到的两个算法:
- 十进制小数转二进制算法:此算法反复乘以 2,取整数部分的值为当前二进制的 bit,直到这个数最终变成 0。这里存在此算法无法在有限次数内收敛的问题,如果此算法拿到的 bit 序列,长度超过尾数位宽(超出了尾数能表示的范围),会导致精度丧失。
- 二进制小数转十进制算法:根据此算法,浮点所能表达的最小的颗粒度为 2-23(十进制的 0.00000011920928955078125),这个类似物理学中的普朗克常量,不可继续切分,若想表达比这个粒度还小的精度,float 无能为力。
根据“最小的颗粒度为 2-23”,我们推定精度比 0.0000001 还小的数,float 无法表示。
从另外一个角度来验证这个事情:
考虑 1.00001、1.000001、1.0000001 几个十进制小数,根据“二进制小数转十进制”的算法,我们得出几者的二进制表示:
1.000001(十进制):
1.0000 0000 0000 0000 0001 0000 1100 0110 1111 0111 1010 0000 1011 0101 1110 1101 1000 11011.0000001(十进制):
1.0000 0000 0000 0000 0000 0001 1010 1101 0111 1111 0010 1001 1010 1011 1100 1010 1111 0100 11.00000001(十进制):
1.0000 0000 0000 0000 0000 0000 0010 1010 1111 0011 0001 1101 1100 0100 0110 0001 0001 1000 0111 01float 型尾数位宽只有 23 位(除去最前面的 1),可以看出:
- 1.0000001,二进制表示的前 23 位皆已丢失。
- 1.00000001,二进制表示的前 26 位皆已丢失(死的很彻底)。
这里断言,从 1.0000001(包括)开始,更高精度的数 float 型都无法表示,验证一下(打脸):
/* ORIGIN 表示原数据
* IEEE 表示实际在内存中存储的 bit 序列
* PRINT 表示再次打印出来是啥
*/
void main(void) {
float f = 1.0000001;
printf("ORIGIN: %s\n", "1.0000001");
// 这里不符合上述断言的预期,从推理上来说尾数部分应该是 0,实际为 1
printf("IEEE : 0x%x\n", *(uint32_t *)&f);
printf("PRINT : %.20f\n", f);
// 这里符合预期
f = 1.00000001;
printf("ORIGIN: %s\n", "1.00000001");
printf("IEEE : 0x%x\n", *(uint32_t *)&f);
printf("PRINT : %.20f\n", f);
}上述程序输出:
ORIGIN: 1.0000001
IEEE : 0x3f800001 <<< 此输出不符合预期
PRINT : 1.00000011920928955078
ORIGIN: 1.00000001
IEEE : 0x3f800000 <<< 符合预期,后面的精度皆已丢失
PRINT : 1.00000000000000000000虽然被打脸了,但基本符合预期,作为一个工程角度的文章,就分析到这里。
如有同学知道何因,敬请告知。
4. 定点数
4.1 基本概念
工程角度来说,定点数的本质就是使用整型变量实现小数运算。
定点数“定”的本质,就是小数点是固定的,小数点后精确的位数是固定的。
定点数的理解有点直觉,请牢记心法:眼中无点,心中有点。
为辅助理解,使用十进制的定点数来讲解。
现在你在一台不支持使用浮点类型的计算机上工作:
- 如果你要执行的算法不需要很高的精度,无需小数位。
这种情况非常简单,所有的数直接用整型表示,该做什么运算就做什么运算。
7 + 2 = 9
7 - 2 = 5
7 * 2 = 14
7 / 2 = 3所有的数本质上是小数位只有 0 位的小数。
- 如果你要执行的算法需要保留小数点后 1 位
这情况下,我们可以使用 10 来表示逻辑上的 1,11来表示逻辑上的 1.1。
那么 35 表示逻辑上的 3.5,15 表示逻辑上的 1.5:
35 + 15 = 50(逻辑上的 5.0)
35 - 15 = 20(逻辑上的 2.0)
35 * 15 = 525(逻辑上的 52.5) <<< 直觉可知需要修正
35 / 15 = 2(逻辑上的 0.2) <<< 直觉可知需要修正从直觉上看,两个定点数的乘除法需要对最终结果进行修正,但是怎么理解这里需要修正?
- 定点数乘法运算的修正
假设计算 3.5 * 1.5,摆出算式:
试问,最终的结果 525,它的小数点应该点在哪?有小学算术底子的应该都知道,点在第一个 5 后面,结果是 5.25。
那在定点数场景下,用 35 表示 3.5,15 表示 1.5,算出来的结果 525,请问逻辑上的小数点应该点在哪?当然与上面一样。
对于 1 位定点数来说,35 * 15 最终的结果要再除以 10,才是最终计算的结果,本质上是因为 35 和 15 都是一个有一个小数位的小数(请默念心法),它们相乘后,会对最终的结果贡献出 2 位的小数部分来(如同 3.5 x 1.5 = 5.25,5.25 其实是有两位小数部分的)。
因而定点数下,需要通过再除以 10(抹去多出来的那个小数位)来对最终的结果进行修正,也就是 52,逻辑上的结果就是 5.2。
- 定点数除法运算的修正
除法的本质与乘法是反着来的,乘法是多出来一个小数位,除法是少了一个小数位。
观察到 3.5 / 1.5 = 2,其结果 2 是一个小数位长度为 0 的数,它丢掉了原本应该有的 1 位小数精度,而其本质应该是 2.0。
如果用 35 / 15,答案还是 2,但是这个 2 是丢掉了 1 位小数精度后的结果,通过乘以 10 来补回丢失的 1 位小数精度,修正结果是 20。
实际工程中,由于计算机的整型运算会自动取整,所以在做定点数运算时,如果先算结果再修正,不可避免会丧失精度(唯一的 1 位小数精度都丢失了)。
要规避这个问题,可以先修正再做除法,其与先做除法再修正逻辑上等价,但可以保留小数部分的精度,也即:
(35 * 10) / 15 = 23,逻辑结果对应 2.3。
- 定点数的加减法无需修正的本质,是因为这此二者运算不会对小数位精度产生影响。
4.2 推广及工程实践
将上一节的基本概念进行推广,假设要执行的算法需要保留小数点后 N 位。
经过上节的分析,应该很好理解,这里罗列几个重要的点即可:
- 将一个逻辑上的数 a 转换成定点表示:a * 10N
- 两个定点数的乘法修正:a * b / 10N(两个 N 位的定点数相乘,结果是 2N 位的定点数,要抹掉多余的 N 位小数)。
- 两个定点数的除法修正:a * 10N / b(最终结果补回 N 位小数)。
对于定点数的四则运算方面我们已经掌握,还剩最后一步比较 tricky 的地方:如何取出一个定点数的整数及小数部分(我们希望能打印出最终的逻辑值)。
下面讨论小数点后为 3 位(N = 3)的定点数 3165。
- 取出整数部分
这个比较简单容易理解,3165 / 103 = 3。
- 取出小数部分
小数部分是 165,直接返回 165 不是不行,但是考虑一个场景:只保留小数点后 1 位。该场景下如何设计一个通用的算法将小数点后只保留 1 位的小数部分返回?
一种可行的手法是,先把 165 x 101(保留小数点后 M 位就乘以 10M),得到 1650,再将 1650 这个定点数取其整数部分即可。说的形象点,就是把想要的小数部分给“挤”到整数位去。
- 实现四舍五入
假设你有一个实实在在的小数 3.165,如何实现四舍五入(小数点后保留 1 位)?
一个可行的算法是,给这个小数,加上 0.05,如此在小数点后第 2 位 >= 5 时,可以产生进位溢出到第 1 位上。
反之不会对第 1 位产生影响。
3.165 + 0.05 = 3.215,保留 1 位小数即是 3.2。
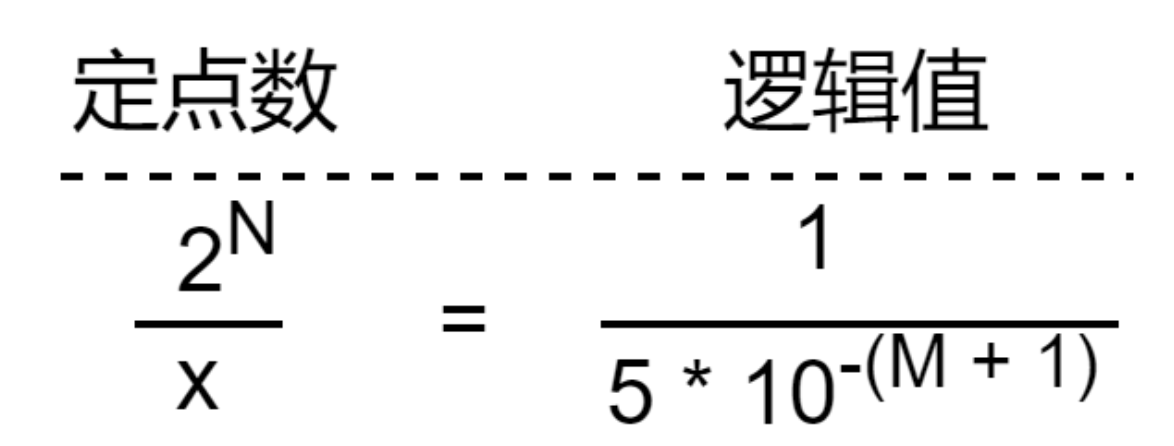
推广到一般情况,针对一个 N 位定点数,我们希望实现保留 M 位,且小数部分的第 M + 1 位四舍五入。
先看个表:
从上图可以看出,若要实现保留 M 位小数点的四舍五入,需要加上 5 * 10N-(M+1) 。
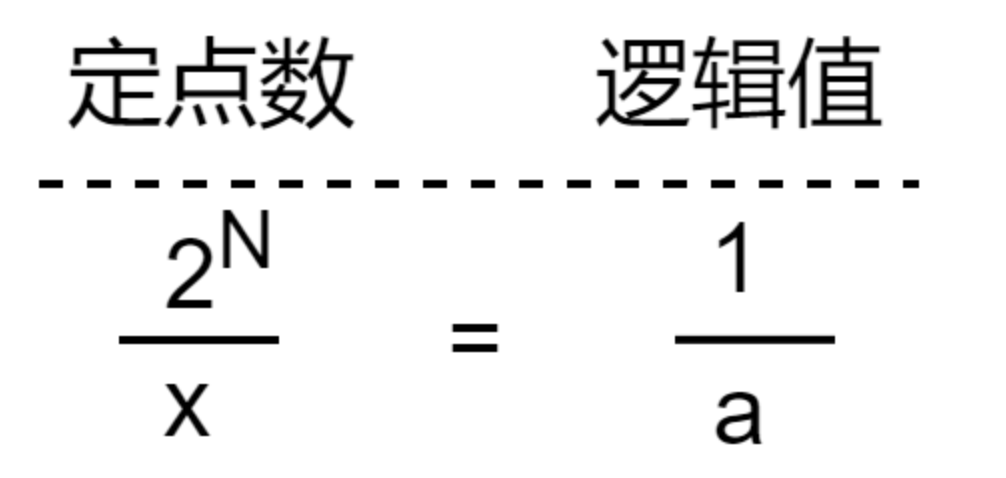
或者,可以从另一个角度来推导。假设要加上的这个数在定点数表示法下为 x,已知定点数表示法下的逻辑 1 为 10N,而我们想要加上的逻辑值为 5 * 10-(M + 1),那么必然满足下式:
解得:
x = 5 \* 10N-(M+1)用简单的代码表示:
// 定义 fixed-point 数类型
typedef unsigned long long fp_t;
// 3 位定点数
#define N 3
// 最终取值保留小数点后 1 位
#define M 1
// 将非定点数转成定点数
fp_t __to_FP(unsigned long long n)
{
return n * pow(10, N);
}
// 获取一个定点数的整数部分
unsigned long long fetch_INT(fp_t n)
{
return n / pow(10, N);
}
// 去掉定点数的整数部分
unsigned long long __wipe_INT(fp_t n)
{
unsigned long long INT = fetch_INT(n);
return n - __to_FP(INT);
}
// 获取定点数的小数部分
unsigned long long fetch_FRAC(fp_t n)
{
return fetch_INT(__wipe_INT(n) * pow(10, M));
}
// 下面是四则运算
fp_t add0(fp_t a, unsigned long long b)
{
return a + __to_FP(b);
}
fp_t add1(unsigned long long a, unsigned long long b)
{
return add0(__to_FP(a), b);
}
fp_t sub0(fp_t a, unsigned long long b)
{
return a - __to_FP(b);
}
fp_t sub1(unsigned long long a, unsigned long long b)
{
return sub0(__to_FP(a), b);
}
fp_t mul0(fp_t a, unsigned long long b)
{
return (a * __to_FP(b)) / pow(10, N);
}
fp_t mul1(unsigned long long a, unsigned long long b)
{
return mul0(__to_FP(a), b);
}
fp_t div0(fp_t a, unsigned long long b)
{
return a * pow(10, N) / __to_FP(b);
}
fp_t div1(unsigned long long a, unsigned long long b)
{
return div0(__to_FP(a), b);
}
// 四舍五入
fp_t fp_round(fp_t a)
{
return a + 5 * pow(10, N - (M + 1));
}
void main() {
/* 3 + 5 = 8
* 8 - 1 = 7
* 7 * 2 = 14
* 14 / 3 = 4.666666
*/
fp_t n = add1(3, 5);
n = sub0(n, 1);
n = mul0(n, 2);
n = div0(n, 3);
// 最终符合预期的输出是 4.6
printf("%llu.%llu\n", fetch_INT(n), fetch_FRAC(n));
// 符合预期的输出是 4.7
printf("%llu.%llu\n", fetch_INT(fp_round(n)), fetch_FRAC(fp_round(n)));
}4.3 二进制定点数
对 10 进制定点数表示法的讨论可以辅助理解,实际工程中 10 进制在运算方面没有 2 进制高效(2 进制可以使用位移代替指数运算),内核在定点数方面的实践即如此。
假设想使用一个整型的低 N 位来表示小数部分,几个关键点在于:
- 将一个逻辑上的数 a 转成定点数表示:a << N(等价于 a * 2N)
因为逻辑上的 1,在定点数表示法下为 1 << N,那么逻辑上的数 a,其在定点数表示法中对应的数 x,满足如下方程:
解得:
x = a * 2N = (a << N)- 两个定点数的乘法修正:(a * b) >> N(多出来 N 个二进制位)
- 两个定点数的除法修正:(a << N) / b(少了 N 个二进制位)
- 取整数部分:a >> N(把低 N 位的小数移除掉)
- 取小数部分:
分两步走:1. 去掉整数部分,也即把整数部分掩掉:a & ((1 << N) - 1),2. 把想要保留的小数部分“挤”到整数位,因为我们要取的是十进制下的 M 位,所以需要对去掉整数部分后的数,乘上 10M,再取整,即 fetch_INT(__wipe_INT(a) * 10M)
- 四舍五入:
与十进制类似,要加上二进制定点数下的逻辑值 5 * 10-(M+1),将十进制下小数点后第 M + 1 位溢出到第 M 位上。
这里的关键在于求出 N 位二进制定点数表示法下,对应逻辑值 5 * 10-(M+1) 的定点数的值。实际上,这个值满足下面的方程:
解得:
x = 2N * 5 * 10-(M+1)代码实现如下:
// 定义 fixed-point 数类型
typedef unsigned long long fp_t;
// 第 N 位用来表示小数位
// 本质上是用 (1 << 11) 表示 1
#define N 11
// 最终取值保留小数点后 1 位
#define M 1
// 将非定点数转成定点数
fp_t __to_FP(unsigned long long n)
{
return n << N;
}
// 获取定点数的整数部分
unsigned long long fetch_INT(fp_t n)
{
return n >> N;
}
// 去掉定点数的整数部分
unsigned long long __wipe_INT(fp_t n)
{
return n & ((1 << N) - 1);
}
// 获取定点数的小数部分
unsigned long long fetch_FRAC(fp_t n)
{
return fetch_INT(__wipe_INT(n) * pow(10, M));
}
// 下面是四则运算
fp_t add0(fp_t a, unsigned long long b)
{
return a + __to_FP(b);
}
fp_t add1(unsigned long long a, unsigned long long b)
{
return add0(__to_FP(a), b);
}
fp_t sub0(fp_t a, unsigned long long b)
{
return a - __to_FP(b);
}
fp_t sub1(unsigned long long a, unsigned long long b)
{
return sub0(__to_FP(a), b);
}
fp_t mul0(fp_t a, unsigned long long b)
{
return (a * __to_FP(b)) >> N;
}
fp_t mul1(unsigned long long a, unsigned long long b)
{
return mul0(__to_FP(a), b);
}
fp_t div0(fp_t a, unsigned long long b)
{
return (a << N) / __to_FP(b);
}
fp_t div1(unsigned long long a, unsigned long long b)
{
return div0(__to_FP(a), b);
}
// 四舍五入
fp_t fp_round(fp_t a)
{
return a + __to_FP(1) * (5 * pow(10, -(M + 1)));
}
void main() {
/* 3 + 5 = 8
* 8 - 1 = 7
* 7 * 2 = 14
* 14 / 3 = 4.6
*/
fp_t n = add1(3, 5);
n = sub0(n, 1);
n = mul0(n, 2);
n = div0(n, 3);
// 符合预期的输出是 4.6
printf("%llu.%llu\n", fetch_INT(n), fetch_FRAC(n));
// 符合预期的输出是 4.7
printf("%llu.%llu\n", fetch_INT(fp_round(n)), fetch_FRAC(fp_round(n)));
}4.4 内核的工程实践
内核的工程实践中,固定使用 11 位的定点数,且固定保留小数点后 2 位,4.3 节中的通用算法将进一步得到简化:
// 相当于 N,11 位二进制定点数
#define FSHIFT 11 /* nr of bits of precision */
// 用 (1 << N) 表示逻辑上的 1
// 相当于 __to_FP(1)
#define FIXED_1 (1<<FSHIFT) /* 1.0 as fixed-point */
// 拿到整数部分。
// 相当于 fetch_INT。
#define LOAD_INT(x) ((x) >> FSHIFT)
// 拿到小数部分,内核实现是固定保留小数点后两位,所以这里 * 100。
// 相当于 fetch_FRAC。
#define LOAD_FRAC(x) LOAD_INT(((x) & (FIXED_1-1)) * 100)要实现定点数小数部的四舍五入,原理是给定点数加上一个值,使其对应小数位溢出。内核中一个使用四舍五入的地方:
/* avenrun[*] 是定点数表示的当前负载
* offset 是要进行四舍五入传入的溢出值
*/
void get_avenrun(unsigned long *loads, unsigned long offset, int shift)
{
loads[0] = (avenrun[0] + offset) << shift;
loads[1] = (avenrun[1] + offset) << shift;
loads[2] = (avenrun[2] + offset) << shift;
}
static int loadavg_proc_show(struct seq_file *m, void *v)
{
unsigned long avnrun[3];
/* 传入 FIXED_1/200,保留 2 位小数下的四舍五入。
* 定点数下的 FIXED_1/200,表示逻辑上的 0.005
*/
get_avenrun(avnrun, FIXED_1/200, 0);
seq_printf(m, "%lu.%02lu %lu.%02lu %lu.%02lu\n",
LOAD_INT(avnrun[0]), LOAD_FRAC(avnrun[0]),
LOAD_INT(avnrun[1]), LOAD_FRAC(avnrun[1]),
LOAD_INT(avnrun[2]), LOAD_FRAC(avnrun[2]));
return 0;
}5. 定点数实现的指数衰退
5.1 通用算法
有了前面详实的铺垫,这一节简单明了,将 2.3 节程序中的浮点型变量,换成定点数。
值得注意的点在于,2.3 节 cal_load 中定义的衰退系数 w = 0.6,要换算成定点数表示下的值(1229),具体转换方法参考 4.3 节,不再赘述。
typedef unsigned long long fp_t;
#define N 11
#define M 1
fp_t __to_FP(unsigned long long n)
{
return n << N;
}
unsigned long long fetch_INT(fp_t n)
{
return n >> N;
}
unsigned long long __wipe_INT(fp_t n)
{
return n & ((1 << N) - 1);
}
unsigned long long fetch_FRAC(fp_t n)
{
return fetch_INT(__wipe_INT(n) * pow(10, M));
}
fp_t add(fp_t a, fp_t b)
{
return a + b;
}
fp_t add0(fp_t a, unsigned long long b)
{
return a + __to_FP(b);
}
fp_t add1(unsigned long long a, unsigned long long b)
{
return add0(__to_FP(a), b);
}
fp_t mul(fp_t a, fp_t b)
{
return (a * b) >> N;
}
fp_t mul0(fp_t a, unsigned long long b)
{
return (a * __to_FP(b)) >> N;
}
fp_t mul1(unsigned long long a, unsigned long long b)
{
return mul0(__to_FP(a), b);
}
fp_t fp_round(fp_t a)
{
return a + __to_FP(1) * (5 * pow(10, -(M + 1)));
}
fp_t cal_load(fp_t last_load, unsigned long long curr)
{
// 1229 是逻辑值 0.6 的定点数表示
static fp_t w = 1229;
return add(mul0(w, curr), mul(__to_FP(1) - w, last_load));
}
void main() {
int i;
fp_t load = 0;
unsigned long long samplings[] = {
[0] = 9,
[1] = 8,
[2] = 7,
[3] = 6,
[4] = 5,
[5] = 7,
[6] = 6,
[7] = 4,
[8] = 2,
[9] = 1,
};
for (i = 0; i < sizeof(samplings) / sizeof(unsigned long long); ++i) {
load = cal_load(load, samplings[i]);
printf("%llu.%llu(%llu.%llu)\n", fetch_INT(load), fetch_FRAC(load), fetch_INT(fp_round(load)), fetch_FRAC(fp_round(load)));
}
}
# 输出,与浮点运算一致,括号内是四舍五入后的数值
5.4(5.4)
6.9(7.0)
6.9(7.0)
6.3(6.4)
5.5(5.6)
6.4(6.4)
6.1(6.2)
4.8(4.9)
3.1(3.1)
1.8(1.9)5.2 内核的工程实践
内核的相关约束更 specific,因而代码反而更简单:
// 11 位定点数
#define FSHIFT 11 /* nr of bits of precision */
// 逻辑 1 在定点数下的表示
#define FIXED_1 (1<<FSHIFT) /* 1.0 as fixed-point */
/* 内核在不同采样周期下的衰退系数,对应的逻辑值分别是:
* EXP_1 = 1884 / 2048 = 0.92
* EXP_5 = 2014 / 2048 = 0.98
* EXP_15 = 2037 / 2048 = 0.99
*/
#define EXP_1 1884 /* 1/exp(5sec/1min) as fixed-point */
#define EXP_5 2014 /* 1/exp(5sec/5min) */
#define EXP_15 2037 /* 1/exp(5sec/15min) */
/* load 是上一轮的负载计算结果,是一个定点数
* exp 是 EXP_1、EXP_5、EXP_15 中的一个
*
* load * exp 为两个定点数相乘,算出来的是历史负载对当前整体负载评估的影响
* 注意,此时这个定点数相乘,结果还没有做修正
*
* n 是当前负载采样,注意 n 传到 CALC_LOAD 之前已经被转成定点数了(采样的逻辑值“乘以”定点数 1)
* n * (FIXED_1 - exp) 算出来的是当前负载采样对整体负载评估的影响
* 注意,此时这个定点数相乘,结果还没有做修正
*
* load += n * (FIXED_1 - exp)
* 将当前采样负载与历史负载的影响相加,就是最终的当前整体负载评估
*
* load >>= FSHIFT
* 因为上面两个定点数相乘尚未做修正,最后统一做修正。
*/
#define CALC_LOAD(load,exp,n) \
load *= exp; \
load += n*(FIXED_1-exp); \
load >>= FSHIFT;CALC_LOAD 中采用的是历史值“乘以”EXP,而不是当前值“乘以”EXP,实际上当前值乘的是 (1 - EXP),这个注意与我们前面代码中对衰退系数的使用是反着来的。
5.3 内核衰退系数的设计
注意看这三个宏内核的代码的注释:
EXP_1,5 秒钟采样一次,1 分钟周期的衰退系数。
EXP_5,5 秒钟采样一次,5 分钟周期的衰退系数。
EXP_15,5 秒钟采样一次,15 分钟周期的衰退系数。对应的逻辑值:
EXP_1 = 1884 / 2048 = 0.92
EXP_5 = 2014 / 2048 = 0.98
EXP_15 = 2037 / 2048 = 0.99拿 EXP_1 来说,5 秒钟一次采样,1 分钟内采样 12 次,根据 2.2 节 式(1),当前 1 分钟采样周期内,最前面一次的采样对当前系统负载的影响权重为:
同理,EXP_5、EXP_15,在采样周期内最前面一次采样的影响权重为:
内核衰退系数的设计,使得每周期最前面的采样值,对当前整体评估的影响忽略不计。
6. 总结
本文分析了定点数和指数衰退算法的底层原理及方法论实践,至于具体这些函数怎么被用来计算负载,调用关系拉一拉即可。
作者: 戴胜冬
文章来源:窗有老梅
推荐阅读
欢迎大家点赞留言,更多Arm技术文章动态请关注极术社区嵌入式客栈专栏欢迎添加极术小姐姐微信(id:aijishu20)加入技术交流群,请备注研究方向。