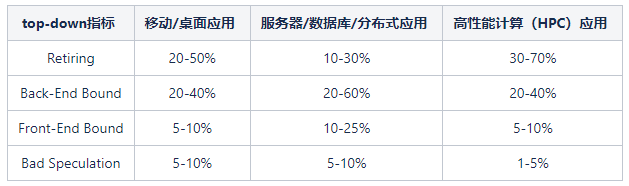
在Intel介绍top-down的演讲中,使用矩阵乘来演示用top-down方法来优化软件性能的过程,如下图所示。 
本文尝试复现这个示例,并且提供更加细节的信息。需要声明的是,本文并不是一篇关于优化矩阵乘法程序的竞赛,重点在于展示利用Top-down分析优化软件性能的过程。
本文使用的测试平台是Intel Xeon Golden 5220,每颗芯片提供18个核心和36个线程。处理器采用Cascade Lake架构,主频2.2GHz。每个核心提供32KB的L1缓存,采用8路组相联结构;每个核心提供1MB的L2缓存,采用16路组相联结构。
baseline测试程序
测试程序需要满足以下要求:
- 矩阵要足够大,一方面提供足够的测试时间,另一方面对于计算和存储系统提供足够的压力。
- 代码要足够简单,尽量少引入系统调用(分配内存,读写文件),避免测试干扰。
矩阵乘的定义是矩阵A[M.K]与矩阵B[K,N]相乘,得到矩阵C[M,N],其中C中的每一个元素计算规则(Ci,j,0<=i<M,0<=j<N)是: 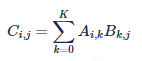
为了满足测试程序的要求,本文将测试程序定义为M=2048,N=2048和K=2048的矩阵乘法。测试程序用C语言编写,矩阵元素是单精度类型。
#define M 2048
#define N 2048
#define K 2048
测试程序的存储使用:
- 一个矩阵的存储空间是2048*2048*4B=16MB,远大于L2缓存。
- 矩阵中一行或一列的存储空间是2048*4B=8KB。
- 由于一个缓存行是64B,矩阵的一行需要占用的缓存空间是128个缓存行。
- 由于矩阵的两行不可能在一个缓存行中,矩阵的一列需要占用2048个缓存行(相当于128KB),远大于L1缓存。
测试程序的流程图如下: 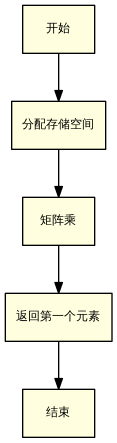
测试程序首先分配A、B、C三个矩阵的空间。然后执行矩阵乘,本文中会不断优化矩阵乘法这一段程序的写法。最后,测试程序返回结果矩阵C的第一个元素C[0][0],防止整段程序被编译器优化掉。
矩阵分配
由于申请的矩阵比较大,存储空间的分配需要采用动态分配。如果要分配一个二维矩阵,那么需要先分配行的指针,再分配行的空间(如下面代码块中上半部分所示)。二维矩阵的元素访问比较简单,但是需要多次调用malloc系统调用。
为了减少系统调用,可以用一维数组代表一个矩阵(如下面代码块的下半部分所示),数组长度是矩阵所有元素。访问一个元素时,需要从根据坐标计算出数组的下标。由于矩阵大小使用宏定义声明的,编译器可以将这些宏定义作为常数优化,不需要真实计算,因此不会引入额外的开销。
// 分配二维空间
float** matrix = (float**)malloc(M * sizeof(float*));
for (mi = 0; mi < 0; mi ++) {
matrix[mi] = (float*)malloc(K * sizeof(float));
memset(matrix[mi], K * sizeof(float), 1.0);
}
// 访问矩阵元素
float item = matrix[mi][ki];
// 分配一维空间
float* matrix = (float*)malloc(M * K * sizeof(float*));
memset(matrix[mi], M * K * sizeof(float), 1.0);
// 访问矩阵元素
float item = matrix[mi * K + ki];
内积矩阵乘
baseline直接按照矩阵乘的定义编写,按照M、N、K的顺序完成三层循环。 
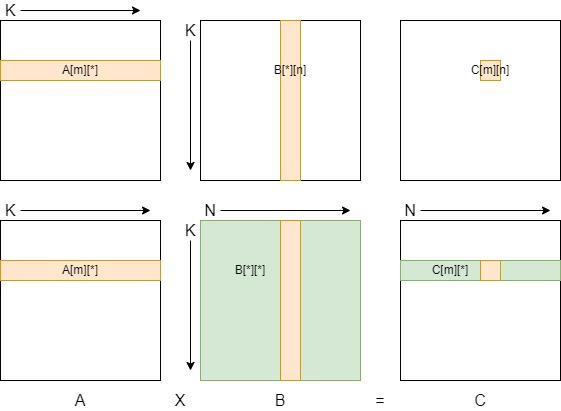
- 最内层的K循环从矩阵A取指定行A[m][*],从矩阵B取指定列B[*][n]。这一行和一列中对应元素相乘,再将所有乘积求和,得到C矩阵中的一个元素C[m][n]。
- 第二层的N循环用矩阵A的同一行A[m][*]对矩阵B的每一列进行重复K循环的操作,得到了结果矩阵中的一行C[m][*]。
- 最外层的M循环对矩阵A的每一行重复操作,得到结果矩阵C。
后文将这种写法为MNK写法。MNK写法的代码如下:
int mi = 0;
int ni = 0;
int ki = 0;
for (mi = 0; mi < M; mi ++) {
for (ni = 0; ni < N; ni ++) {
for (ki = 0; ki < K; ki ++) {
result[mi * N + ni] = result[mi * N + ni] + left[mi * K + ki] * right[ki * N + ni];
}
}
}
测试结果
对于baseline测试程序,采用两种编译方式:
- 不进行任何优化(mnk):-g -Wall
- 开启编译器优化(mnk\_o2):-O2 -g -Wall
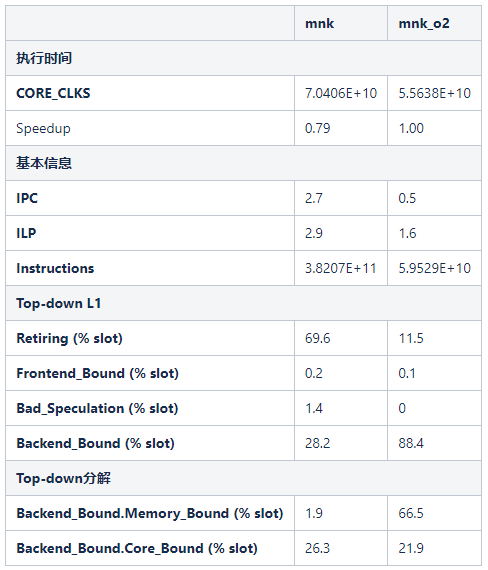
编译器优化O2使得指令的执行时间得到改善,同时程序的指令分布和执行状态发生了巨大的变化。考虑到-O2选项是常规优化选项,所以将mnk\_o2的执行时间作为加速比计算的基准。
首先,编译器优化显著减少了指令的数量,mnk程序的指令数是mnk\_o2程序的5.6倍。不启动编译器优化时,编译器按照代码进行直译。当启动编译器优化时,编译器会优化寄存器分配和指令执行顺序,从而减少指令数量。通过观察反汇编代码,至少可以发现两处优化:
- 考虑到宏定义的常量,简化了地址的计算。不开启O2优化时,程序忠实进行ki * N + ni计算(只是将乘法变成了移位)。开启O2优化后,程序直接将N作为地址累加的步长。
- 在寄存器中复用数据。不开启O2优化时,程序忠实从内存读取结果矩阵的值,然后累加,并会写到内存。开启O2优化后,result[mi * N + ni]会被存放在寄存器中,直至完成K循环之后再写入内存。
但是执行时间并没有同等程度的得到提升,mnk\_o2程序的执行速度只提升了25%。指令的IPC也从2.7降低到0.5,ILP从2.9降低到1.6。这表示指令数虽然减少了,但是编译器将冗余指令大部分都优化掉了,剩余的指令之间的依赖关系变得非常强烈,硬件无法通过指令级并行来优化性能。这也从另一个角度说明了现代高性能处理器通过超标量和乱序执行对于程序的ILP进行了充分的挖掘。
接着,Top-down分析发现,Frontend\_Bound和Bad\_Speculation的比例很低,这是符合预期的。程序的代码段很小,不会引起ITLB和ICache的频繁缺失。程序中的循环长度固定,绝大部分分支都是Taken,分支预测率很高。Retiring的比例从69.6降低到11.5,Backend\_bound的比例从28.2提升到88.4,这两处变化也与指令数和ILP的变化相一致。这一组数据说明,retiring占比越高,可以表明流水线的效率越高,但是不能表示程序性能一定会更好。
最后,利用Top-down的决策树对于性能瓶颈进行分解,如下图所示。
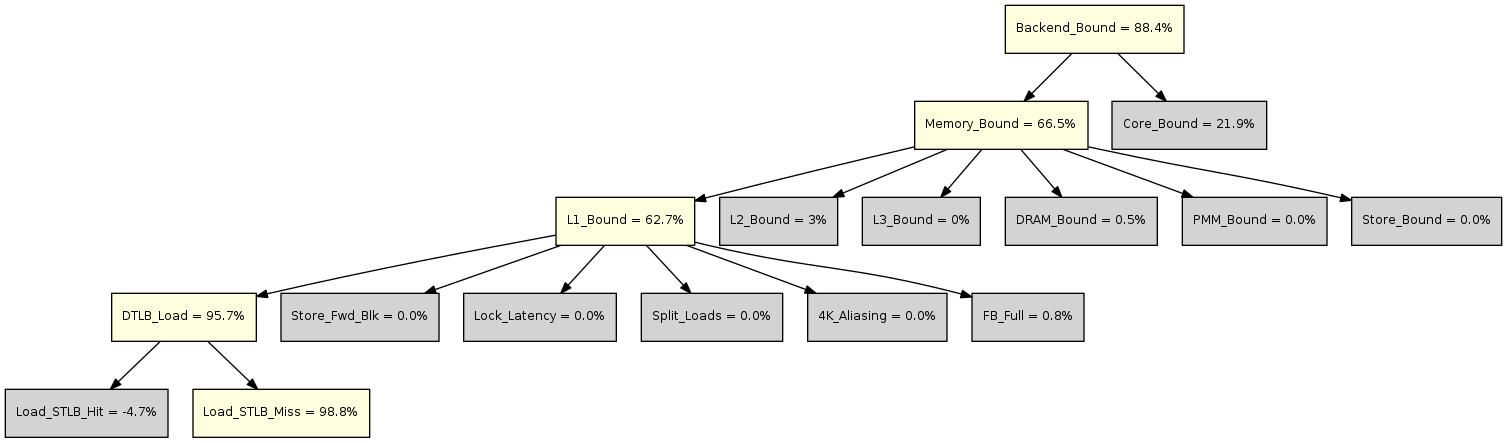
图中黄色表示值得关注的度量,灰色表示暂时忽略的度量。
- 在L2,Memory\_Bound表示流水线因为存储系统瓶颈而空闲的slot的比例,用于估计流水线可能因为load或store指令而stall的slot比例。主要原因包括:未完成的load阻塞后续指令,等待完成的store指令反压等。
- 在L3,L1\_Bound表示流水线因为load访存阻塞的周期的比例,但是这些load并不是L1数据缓存缺失。主要原因包括:DTLB缺失等。
- 在L4,DTLB\_Load表示流水线因为L1 DTLB缺失的访存而阻塞的周期的比例;
- 在L5,Load\_STLB\_Miss表示流水线因为L1 DTLB缺失而且L2 TLB也缺失的访存而阻塞的周期的比例。
上图中的决策树指出,程序中存在大量的TLB缺失(L1 DTLB和L2 TLB都缺失)。一个矩阵的一行占用了8KB存储空间,需要2个4KB页表。那么访问矩阵一列的时候,每一个元素都不在同一个页表中。访问矩阵的一列需要2048个4KB页表。但是处理器DTLB只提供128个4KB页表单元。这就意味着,对于列方向的循环会反复引起DTLB缺失。而MNK写法把列方向的循环放到了三层循环的最低层,这就导致了大量DTLB缺失。
使能大页面
默认情况下,OS使用4KB的页面(page)进行内存管理和地址映射。但是为了应对大数据量的应用,现代处理器和OS都支持超过4KB的页面,常见的有2MB/1MB/1GB的大页面。Linux系统称为Huge Page。本文先尝试用大页面来优化DTLB缺失。
使能2MB页面
首先,我们要为处理器设置页面资源。用下面的命令为OS设置100MB的4KB页面。
> sudo sysctl -w vm.nr_hugepages=102400
> grep Huge /proc/meminfo
AnonHugePages: 0 kB
ShmemHugePages: 0 kB
FileHugePages: 0 kB
HugePages_Total: 26138
HugePages_Free: 26138
HugePages_Rsvd: 0
HugePages_Surp: 0
Hugepagesize: 2048 kB
Hugetlb: 53530624 kB
接着,在测试程序代码中用mmap API创建大页面存储。
// 引入mmap API头文件
#include <sys/mman.h>
// 替换baseline中malloc分配
left = (float*)mmap(NULL, M*K*sizeof(float), PROT_READ|PROT_WRITE, MAP_PRIVATE|MAP_ANONYMOUS|MAP_HUGETLB, -1, 0);
right= (float*)mmap(NULL, K*N*sizeof(float), PROT_READ|PROT_WRITE, MAP_PRIVATE|MAP_ANONYMOUS|MAP_HUGETLB, -1, 0);
result=(float*)mmap(NULL, M*N*sizeof(float), PROT_READ|PROT_WRITE, MAP_PRIVATE|MAP_ANONYMOUS|MAP_HUGETLB, -1, 0);
第一个参数表示了期望分配的地址,一般不需要提供(NULL),第二个参数表示分配空间的大小。第三个参数标志分配的页面的权限:PROT\_READ和PROT\_WRITE表示分配空间的权限为可读可写。第四个参数表示分配的标识:MAP\_PRIVATE表示分配的空间为此程序私有;MAP\_ANONYMOUS表示存储空间没有文件与之对应,存储空间会被初始化为零;MAP\_HUGETLB表示使用大页面(2MB)创建页面。第五个参数和第六个参数指定分配页面对应的文件:第五个参数指定文件标识符,第六个参数标识文件的偏移。
测试结果
对于大页面测试程序,开启编译器优化(mnk\_bigtlb):-O2 -g -Wall 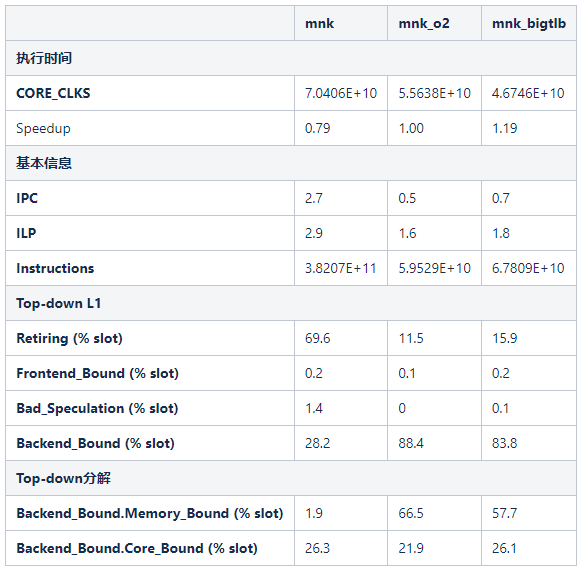
使用的大页面只将执行速度提升19%。观察Backend\_Bound.Memory\_Bound.L1\_Bound.DTLB\_Load度量也变成了零,这表明程序已经按照2MB的大页分配页面。
但是Top-down分析显示性能瓶颈仍然是Memory\_Bound。当问题比较复杂的时候,性能瓶颈可能由多个问题功能构成。Top-down方法聚焦于优先需要优化的性能瓶颈。优化了这个性能瓶颈之后,才会暴露出了被隐藏的性能瓶颈。
利用Top-down的决策树对于性能瓶颈进行分解,如下图所示。 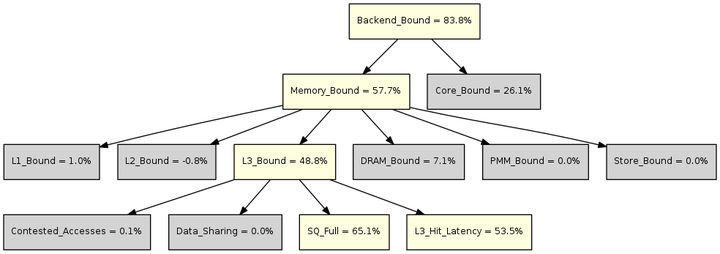
图中黄色表示值得关注的度量,灰色表示暂时忽略的度量。
- 在L2,Memory\_Bound表示流水线因为存储系统瓶颈而空闲的slot的比例,用于估计流水线可能因为load或store指令而stall的slot比例。主要原因包括:未完成的load阻塞后续指令,等待完成的store指令反压等。
- 在L3,L3\_Bound表示流水线因为L3命中的load访存而阻塞的时钟周期的比例。
- 在L4,SQ\_Full表示流水线因为Super Queue(SQ)满导致阻塞的周期数比例,SQ可以理解为L2访问L3的队列。L3\_Hit\_Latency表示流水线因为L3访问流水线而阻塞的时钟周期的比例。
上图中的决策树指出,程序中存在明显的缓存缺失的问题。由于矩阵大小宽度大于1个缓存行,列访问的每一个元素都处于不同的缓存行。获取矩阵的一列需要2048个缓存行。但是L1数据缓存总共只提供了512个缓存行。读取矩阵的一列会引起大量的缓存缺失。MNK写法的内层K循环存在列访问,这对于缓存是非常不友好的。
交换循环
如上面分析,由于存在列方向的访问,MNK写法的循环对于缓存是非常不友好的。为了优化内存访问,最理想是在内存循环尽量使用行访问。通过交换M、N和K的顺序,发现按照M、K、N顺序进行循环,可以满足这一需求。
MKN循环
按照M、K、N顺序进行循环的。 
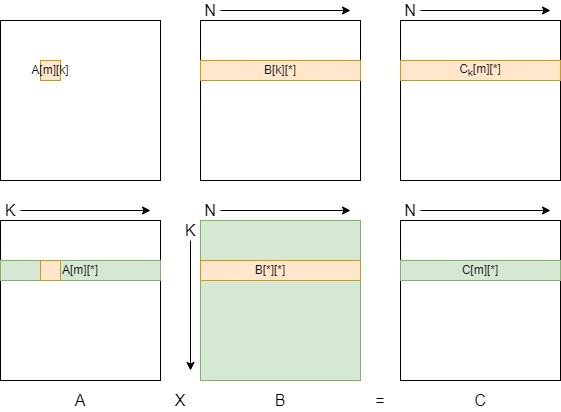
- 最内层的N循环从矩阵A取一个元素A[m][k],从矩阵B取一指定行B[k][*]。这一元素和一行中对应元素相乘,得到C矩阵中的一个行的部分和Ck[m][*](下标k标识指定k的部分和)。
- 第二层的K循环取矩阵A的指定行A[m][*],将这一行的每一个元素和矩阵B的对应行重复N循环操作,得到的结果累加在一起,得到C矩阵中的一行C[m][*]。
- 最外层的M循环对矩阵A的每一行重复操作,得到结果矩阵C。
后文将这种写法为MKN写法。MKN写法的代码如下:
int mi = 0;
int ni = 0;
int ki = 0;
for (mi = 0; mi < M; mi ++) {
for (ki = 0; ki < K; ki ++) {
for (ni = 0; ni < N; ni ++) {
result[mi * N + ni] = result[mi * N + ni] + left[mi * K + ki] * right[ki * N + ni];
}
}
}
MKN写法不仅可以优化访存,还可以优化程序的ILP。在MNK中,后一次K循环的乘积需要累加到前一次K循环的结果上,程序最内层循环存在迭代依赖。MKN的最内层循环不存在这样的迭代依赖,可以释放ILP。
测试结果
对于MKN写法测试程序,开启编译器优化(mkn\_o2):-O2 -g -Wall 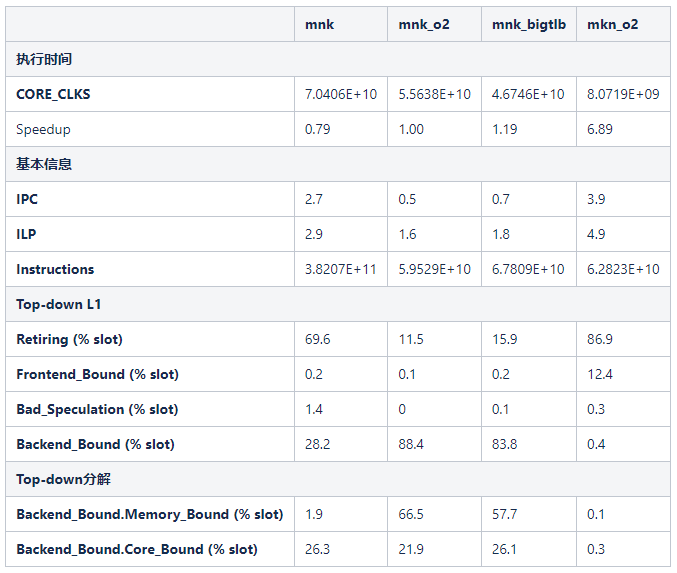
mkn\_o2程序的执行时间相比于mnk\_o2的时间获得非常显著的改善,mnk\_o2的执行时间是mnk\_bigtlb的5.8倍。
首先,程序的并发性得到了显著提升,ILP达到了4.9。这是一个非常好的效果,cascade的dispatch带宽才是6。
接着,Top-down分析发现,Frontend\_Bound和Bad\_Speculation的比例仍然很低,这是符合预期。Retiring占比达到了86.9%,Backend\_Bound减低到了0.4%,这再次证明了交换循环次序的优化是非常有效的。
对于继续优化的方向,Top-down的报告给我们提供了一点提示。 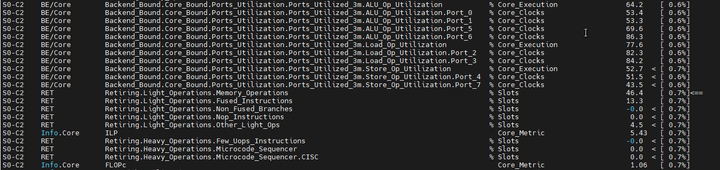
如图中箭头所示,系统瓶颈是退休的slot中,访存占用的操作过多。这里的潜台词是,指令的数据吞吐率过小。对于矩阵乘这样的数据密集型的程序,采用标量指令(一条指令处理一组数据)处理显然是不合理的,向量化必然的方向。
使能向量化和FMA
x86向量化和FMA
对于矩阵乘这样的数据密集型的程序,引入SIMD向量化时必然的。标量指令都是一条指令只能操作一组数据。SIMD的意思是,一条指令操作多组数据,这些数据都进行相同的操作。
x86指令集提供的SIMD指令集包括MMX、SSE、AVX和AVX512四个扩展指令集:
- MMX使用64比特向量,只支持标量操作。
- SSE使用128比特向量(xmm寄存器),支持标量和浮点操作。
- AVX使用256或向量(ymm寄存器),支持标量和浮点操作。
- AVX512使用512比特向量(zmm寄存器),支持标量和浮点操作。AVX512还提供FMA操作,即一条指令完成乘和加两个操作,从而进一步减少指令数。
使用向量化有两种方法:
- 一种方法是利用Intrinsics API的方式,直接编写向量化代码。编译器几乎是按照内嵌汇编的方式处理Intrinsics API,从而保证能够得到用户预期的代码序列。
- 另一种方式是通过编译器自动完成向量化。GCC选项-ftree-vectorize可以开启向量。如果是整形计算,编译器采用MMX指令集;如果浮点计算,编译器采用SSE指令集。
- 编译器倾向于向量化最内层循环。如果内层循环不方便并行化,编译器也会自行判断哪一层循环更加适合展开。比如对于M、N、K的循环,编译器向量化是的N层循环。
- 如果需要使用更新的指令集,可以给编译器指定处理器微架构或者指定指令集。请查看GCC的相关文档。
测试结果
在本文的测试中,针对MKN写法程序,通过编译器选项开启SSE或AVX向量化。
- 启动SSE向量化(mkn\_sse):-ftree-vectorize -g -Wall。
- 启动256比特AVX向量化(mkn\_avx):-O2 -ftree-vectorize -mavx2 -g -Wall
- 启动512比特AVX向量化和FMA指令(mkn\_avx512):-O2 -ftree-vectorize -mavx512f -g -Wall。
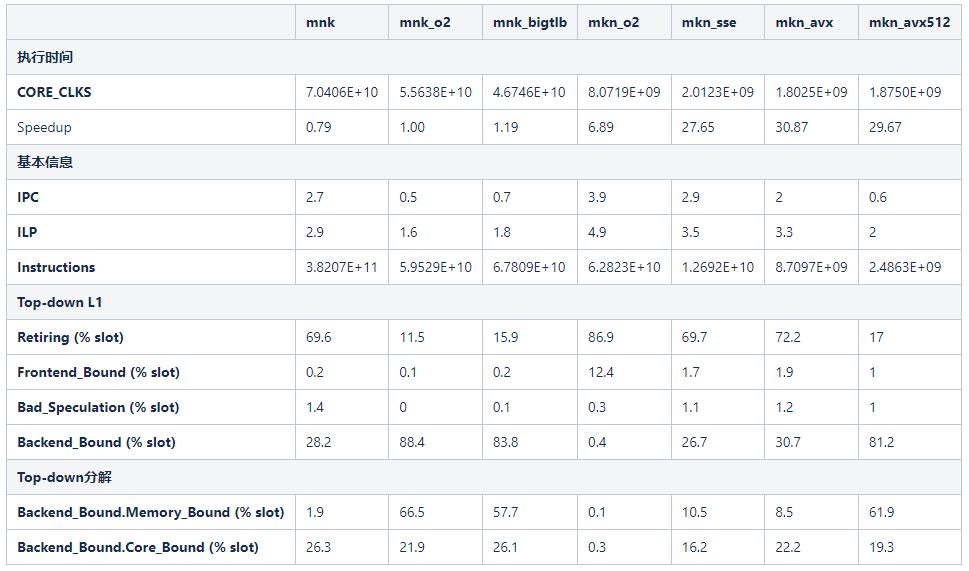
向量化程序的执行时间相比于mkn\_o2的时间再次获得非常显著的改善。使用SSE向量化的mkn\_sse的执行速度是mnk\_o2的27.65倍。理论上一条SSE指令(128比特)相当于4条标量指令(32比特)。mkn\_sse是mkn\_o2的4倍,这与理想情况非常接近。表示数据吞吐率不高正是mkn\_o2的性能瓶颈。
但是mkn\_avx和mkn\_avx512相对于mkn\_sse的性能提升并不明显。mkn\_avx512相对于mkn\_sse虽然有11%的性能提升。但是Retiring比例降低到了17,Backend\_Bound比例上升到了81.2。这表明随数据吞吐率增加,程序出现了新的性能瓶颈。
利用Top-down的决策树对于性能瓶颈进行分解,如下图所示。
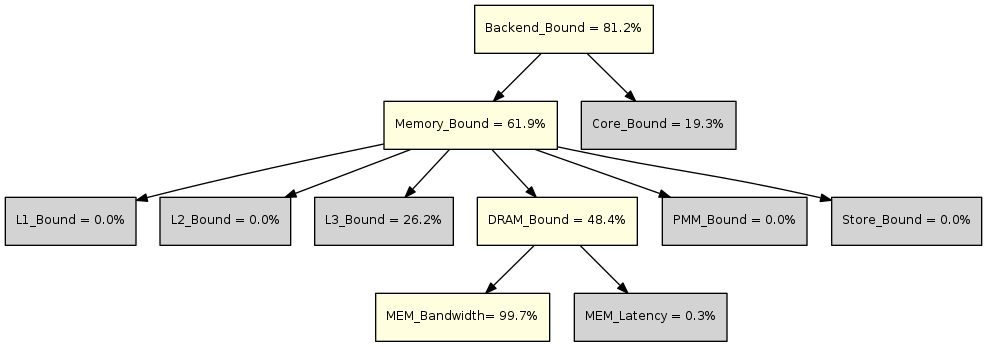
图中黄色表示值得关注的度量,灰色表示暂时忽略的度量。
- 在L2,Memory\_Bound表示流水线因为存储系统瓶颈而空闲的slot的比例,用于估计流水线可能因为load或store指令而stall的slot比例。主要原因包括:未完成的load阻塞后续指令,等待完成的store指令反压等。
- 在L3,DRAM\_Bound表示流水线因为访问外部存储(DRAM)的load访存阻塞的时钟周期的比例。
- 在L4,MEM\_Bandwidth表示流水线因为DRAM带宽限制而阻塞的时钟周期比例。
上图中的决策树指出,程序中出现了大量的的缓存缺失。处理器核心的load带宽是128B,一条标量指令需要的带宽是处理器load带宽的32分之一,但是一条AVX512指令需要的带宽是处理器load带宽的二分之一。如果标量程序中,一笔访存的128B数据可以用Q条计算指令取掩盖;那么使用AVX512指令时,一笔访存的128B数据只用Q/16条计算指令来掩盖。因此,计算吞吐率的提高,处理器对于数据消耗的速度成倍增加。矩阵乘的MKN写法已经不能满足计算对于数据的需求。
矩阵复用
当数据吞吐率快速提升的情况下,单纯交换循环次序已经不能满足计算对于数据的需求。需要考虑如何在计算过程中实现数据在L1缓存中的复用,通常的做法是将内层循环再分块,复用内层循环的数据。
矩阵分块复用
将矩阵在K和N方向进行分块,按照分块进行K、N、M的循环。 
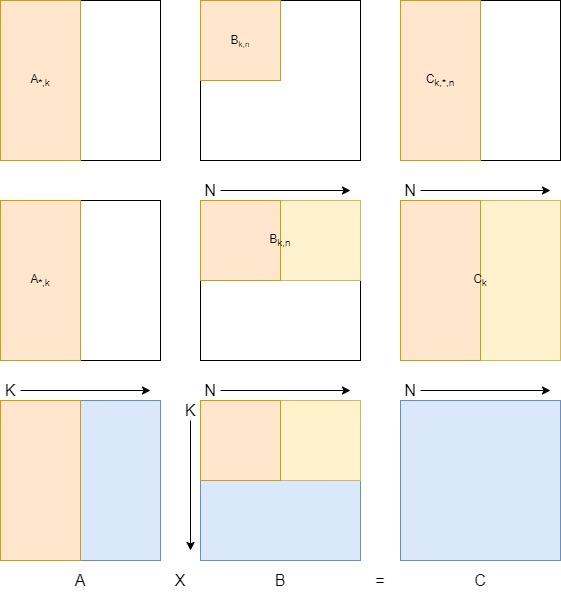
- 将矩阵A和矩阵C按照列分块(A*,k和C*,n),矩阵B行列都分块(Bk,n)。将矩阵A的一块(A*,k)与矩阵B的一块(Bk,n)进行矩阵乘,可以得到矩阵C的一块(Ck,*,n),这里都是k分块的部分和。这里的子矩阵还是采用MKN方式。
- 在N方向遍历矩阵B的同一行的分块,分别于矩阵A的同一个分块(A*,k)相乘,可以得到矩阵C的一组部分和(Ck)。
- 最后遍历矩阵A的分块,最终得到矩阵C的全部。
在整个计算过程中,矩阵B的分块会被复用,数据可以驻留在L1数据缓存中。
后文将这种写法为KNMKN写法。KNMKN写法的代码如下:
#define SLICE_N 64
#define SLICE_K 64
int mi = 0;
int ni = 0, ni_o = 0;
int ki = 0, ki_o = 0;
for (ki_o = 0; ki_o < K; ki_o += SLICE_K) {
for (ni_o = 0; ni_o < N; ni_o += SLICE_N) {
for (mi = 0; mi < M; mi ++) {
for (ki = ki_o; ki < SLICE_K + ki_o; ki ++) {
for (ni = ni_o; ni < SLICE_N + ni_o; ni ++) {
result[mi * N + ni] = result[mi * N + ni] + left[mi * K + ki] * right[ki * N + ni];
}
}
}
}
}
测试结果
对于KNMKN的测试程序,开启编译器优化、向量化和FMA(knmkn):-O2 -ftree-vectorize -mavx512f -g -Wall。
程序中采用[64,64]的分块,每个分块占用的存储空间为:64*64*4B=16KB,与L1数据缓存大小相同。 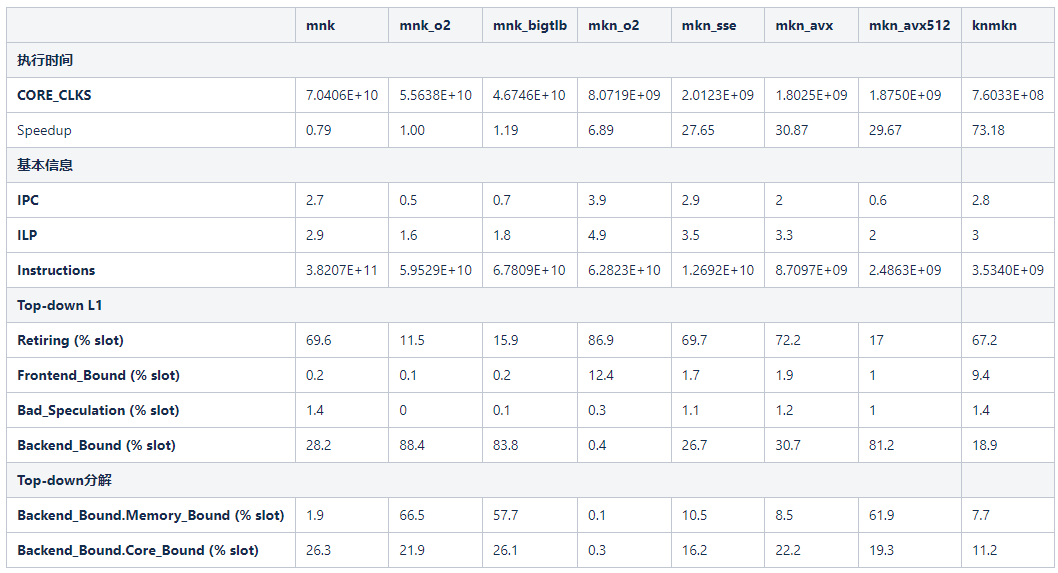
矩阵分块复用再次显著提升了测试程序的性能。knmkn的执行速度相对于mkn\_avx512提升来2倍,相对于mkn\_sse提升了3倍。
同时,Top-down分析结果显示,Retiring占比提升到66.8%,Backend\_bound占比降低到26.5%。这表明,通过在L1缓存中复用矩阵,可以显著减少缓存缺失的情况,从而提升性能。
knmkn程序的性能和表现于分块大小有很大的关系。比如,采用[32,32]的分块,那么性能提升就不明显。这里需要平衡指令流和缓存访问,本文不赘述相关尝试。
总结
首先,本文不是一个矩阵乘性能优化的竞赛,而是希望以矩阵乘为例,展示top-down方法如何知道软件性能优化,以及在优化过程中的注意事项。在本文中,根据top-down分析结果,先后优化了大页面、循环次序、向量化和数据复用。相对于直接遵循矩阵乘定义的mnk方法,优化后的knmkn程序获得了74.5倍性能提升。这个结果只代表本文的测试程序和测试平台,并不具有可迁移性。矩阵形状的不同、处理器平台的变化以及当前处理器的负载情况都可能对这个数据造成影响。 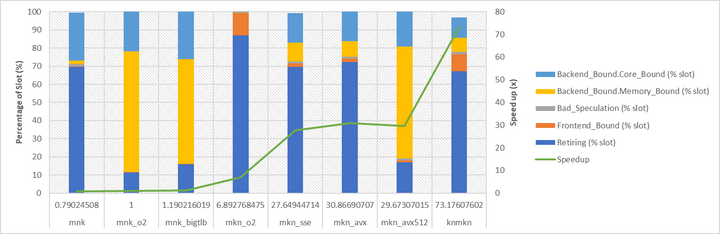
上图展示了我们优化过程中,程序执行速度的提升情况以及Top-down分布的变化。由于Core\_Bound和Memory\_Bound的重要性,将这两个L2的指标和L1指标画在了一张图中。
Top-down不能直接用来评估软件的性能。Retiring占比越高,表示流水线效率越高,但是软件性能并不是最好的。比如mnk、mnk\_o2程序的Retiring比例都很高,但是仍然有明显的优化空间。
Top-down能够为软件优化提供指导,能够给出目前需要首要解决的性能瓶颈。但是并不是所有的性能瓶颈。对于复杂的场景,性能瓶颈可能由多种原因共同引起。Top-down只能展示出其中一种原因。当首要性能瓶颈解决后,才能展露出另一种性能瓶颈。
随着性能优化的进行,性能瓶颈是不断变化的,Top-down的分析结果也是不断变化的。mnk程序表现为Memory\_Bound,通过引入大页表和调整交换顺序解决了这个瓶颈。从mkn\_o2开始,程序表现为吞吐率不足。随着引入并行化,到了mkn\_avx512程序再次表现为Memory\_Bound。
Intel根据经验,对于不同类型的应用的top-down分析结果进行了总结:
- 服务器/数据库/分布式程序表现为Retiring比例最少,Front-end Bound和Back-end Bound都比较明显。原因在于,从CPU的角度来看,这类应用的任务执行时间较短,而且相邻任务之间没有关系,导致处理器经常需要面对一个新任务的启动和迁移,从而表现为指令缓存命中率、数据缓存命中率以及分支预测效率不高。
- 高性能计算的Retring比较最高,原因在于这类应用执行时间较长,具有比较单一的模式,可以通过软件优化实现较理想的数据复用和非常理想的分支预测,使得程序的执行效率很高。本文中的矩阵乘就属于这一类型。
- 移动或桌面应用程序的因为类型多样,表现相对平均。
以上数据适用于已经很好优化后的程序。本文的示例也符合这一个统计规律。这个数据可以作为性能优化目标的参考。