做控制时,大家经常会有这样的感受“代码很丰满,现实很骨感”,这是因为将计算机指令转移到实际硬件时,由于物体的惯性以及各种非理想化的因素影响,往往会出现实际与预期不符合的情况。
这篇文章将以“操控遥控飞机从地面飞到10米高度并悬停”为例子,用最通俗易懂的方式,让你理解PID。在这个问题中,我们假设加速度是可以直接调控的(实际生活中往往也是这样),因此,我们输入的量为加速度的大小和方向(正负),而我们最终想要得到的结果就是高度稳定在10米。
1. 首先我们来讲控制方法:
控制方法主要分为“开环控制”和“闭环控制”,这两种控制方法的简单理解为:
开环控制:计算出飞机从地面到10米高度所需要的加速度以及作用时间,然后将其编写为一条固定的指令,“一次执行,全过程受益”。
闭环控制:在飞机飞行的过程中,系统时刻关注飞机的状态,并做出相应的调整。而PID控制就是最常用的闭环控制。
2. PID原理
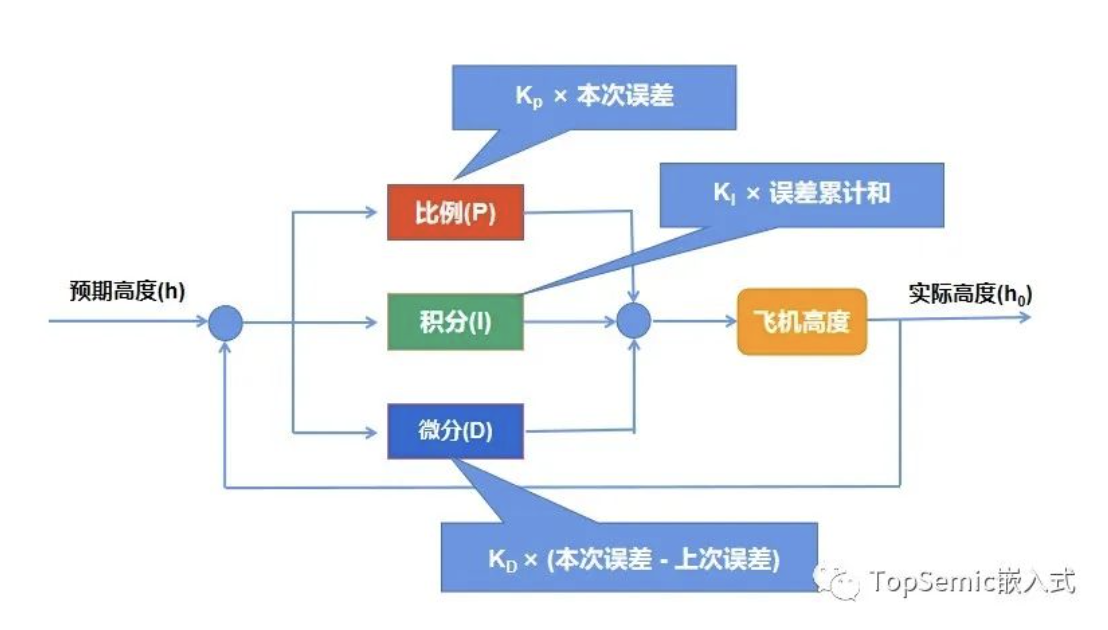
一讲到原理,很多人都会搬出PID公式,数学较好或者学过自控的人还好,要是遇见一个半路转行做控制的,看见“微分”和“积分”,头都大了。其实,由于生活中信号采样具有一定的间隔,因此我们经常遇见的都是离散信号的控制,只需要读懂下图即可:
3. 实践出真知(python实现PID)
3.1 导入包
`import time`
`import matplotlib.pyplot as plt`3.2 PID实现
# 实现一个PID控制器
class PIDController:
def __init__(self, kp, ki, kd):
"""
初始化PID控制器
参数:
kp (float): 比例系数
ki (float): 积分系数
kd (float): 微分系数
"""
self.kp = kp # 比例系数
self.ki = ki # 积分系数
self.kd = kd # 微分系数
self.prev_error = 0 # 上一次的误差
self.integral = 0 # 误差积分值
def calculate(self, setpoint, current_value):
"""
计算PID控制器的输出
参数:
setpoint (float): 设定值(目标值)
current_value (float): 当前值(被控制的系统当前状态)
返回:
output (float): 控制器的输出
"""
error = setpoint - current_value # 计算误差
self.integral += error # 更新误差积分
derivative = error - self.prev_error # 计算误差导数
output = self.kp * error + self.ki * self.integral + self.kd * derivative
# 计算控制输出,包括比例、积分和微分部分
self.prev_error = error # 保存当前误差作为下一步的上一次误差
return output # 返回控制器的输出3.3 飞行器模拟
#飞行器模拟
class AircraftSimulator:
def __init__(self):
self.height = 0 # 飞行器初始高度为0
self.velocity = 0 # 飞行器初始速度为0
def update(self, throttle, time_step):
"""
更新飞行器状态:高度和速度
参数:
throttle (float): 油门输入,控制引擎输出的力量
time_step (float): 时间步长,模拟器更新的时间间隔
"""
acceleration = throttle - 0.1 * self.velocity
# 根据简化的动力模型计算飞行器的加速度
# 加速度等于油门输入减去速度的一部分,这是简化的模型
self.velocity += acceleration * time_step
# 根据加速度更新速度
# 新速度等于当前速度加上加速度乘以时间步长
self.height += self.velocity * time_step
# 根据速度更新飞行器的高度
# 新高度等于当前高度加上速度乘以时间步长3.4 主函数与绘图
# 主函数
def main():
# PID参数
kp = 5.0
ki = 0.1
kd = 10
# 初始化PID控制器和飞行器模拟
pid_controller = PIDController(kp, ki, kd)
aircraft_simulator = AircraftSimulator()
target_height = 10.0
time_step = 0.1
total_time = 20 # 总模拟时间增加到20秒
current_time = 0.0
# 存储时间和高度数据的列表
time_data = []
height_data = []
# 模拟循环
while current_time < total_time:
# 使用PID控制器计算控制信号
control_signal = pid_controller.calculate(target_height, aircraft_simulator.height)
# 添加扰动
disturbance = -1.5
control_signal += disturbance
# 使用控制信号和时间步长更新飞行器模拟
aircraft_simulator.update(control_signal, time_step)
# 存储时间和高度数据
time_data.append(current_time)
height_data.append(aircraft_simulator.height)
current_time += time_step
time.sleep(time_step) # 添加时间延迟以模拟实时行为
print("Simulation completed.")
# 绘图
plt.plot(time_data, height_data, label='Height')
plt.axhline(y=target_height, color='r', linestyle='--', label='Target Height')
plt.xlabel('Time (s)')
plt.ylabel('Height (m)')
plt.title('Aircraft Height Control with Random Disturbance')
plt.legend()
plt.grid(True)
plt.show()
if __name__ == "__main__":
main()4. 实验与参数理解
PID的控制经常会涉及到KP、KI、KD三个参数的调节,如果盲目调节则会花较长时间,接下来我们将用直观实验来理解以下几个参数的具体含义。
4.1 比例环节
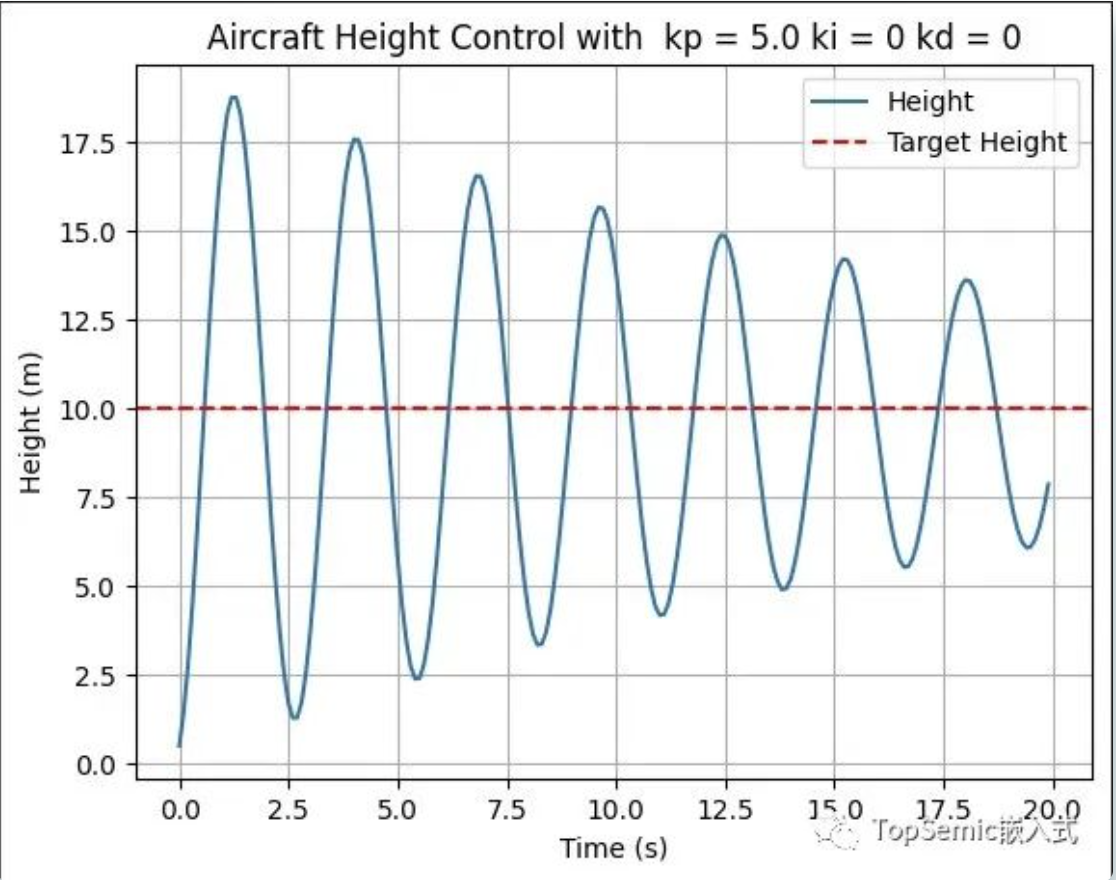
计算公式为KP × 误差,具体的含义即为误差越大,值越大。这一点是非常直观的,误差越大则说明偏离预期值越远,我们要加大“油门”,快速调整!以下是当KI、KD为0,只有KP=5的测试结果:
从图中我们可以看到虽然慢慢的想10收敛,但由于误差越大,其“油门”越大,就像是一个“莽夫”,尽管每次都在调整,但总是用力过猛!
4.2 微分环节
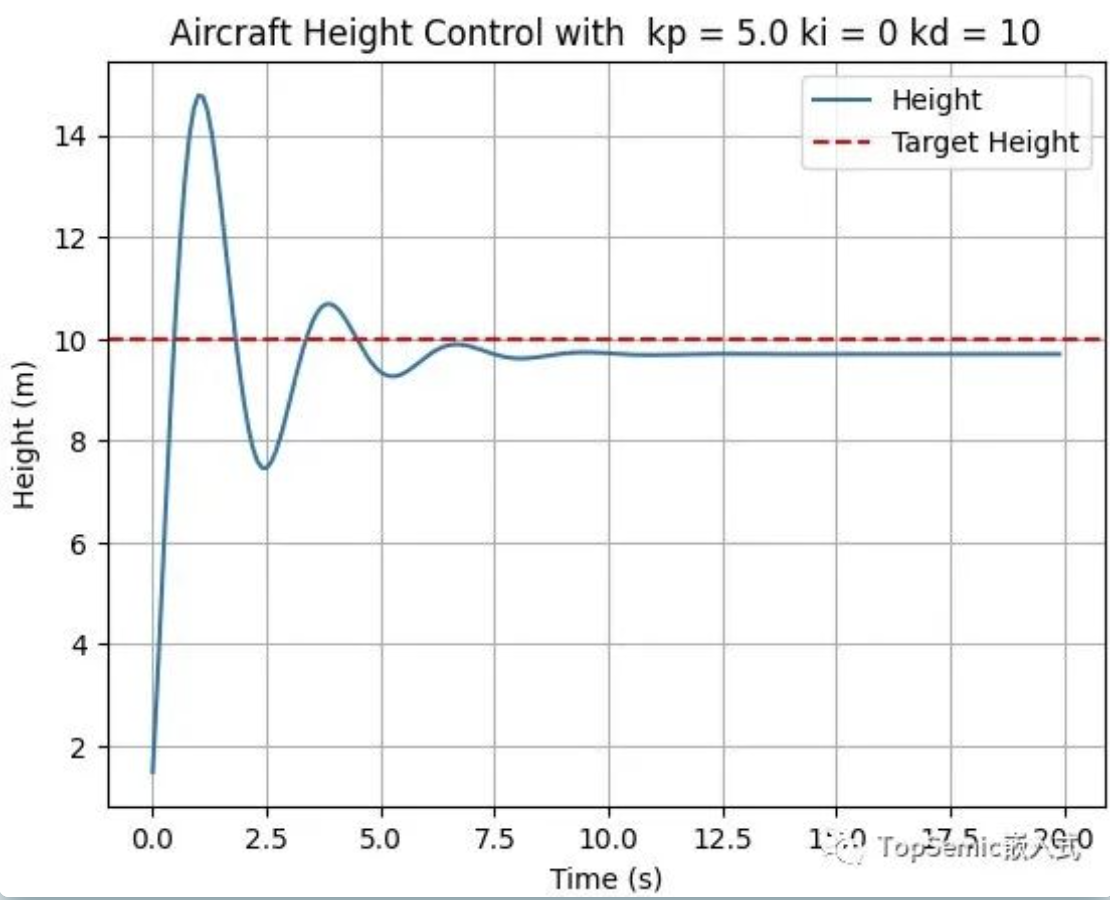
计算公式为KD × (本次误差 - 上次误差),对于这个公式,我们可以理解为用来中和“用力过猛”。以下是当KP=5、KD=10、KI=0的测试结果:
显然,这个结果要比上次好很多,但始终低于10,这是因为我们在模拟中加入了一个干扰条件:
# 添加扰动
disturbance = -1.5
control_signal += disturbance因此,要想消除这个干扰,就需要积分环节的加入。
4.3 积分环节
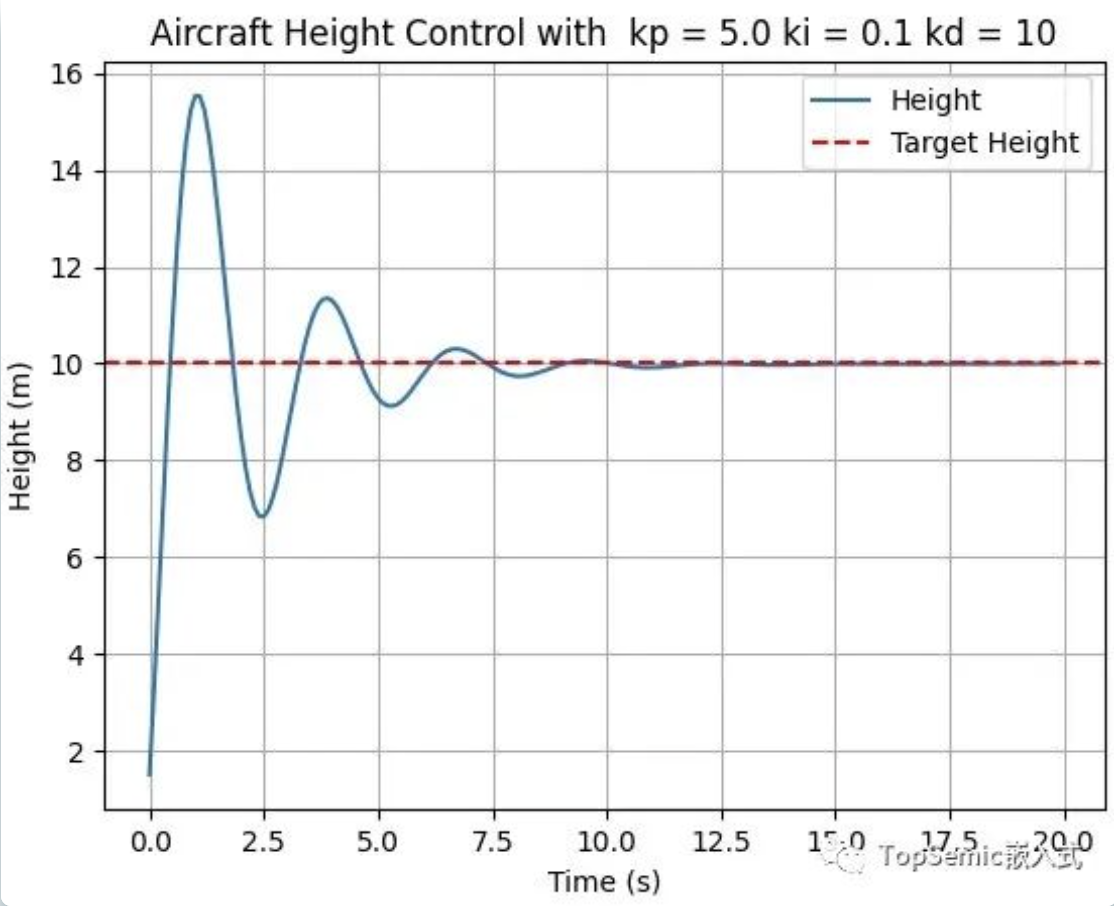
积分环节的公式为KI × 误差累计和,用官方的语言来说,用来调整“稳态误差”,其实,所谓的稳态误差就可以理解为“一直存在的误差”,也就是在本次实验中加入的持续干扰!以下是当KP=5、KD=10、KI=0.1的测试结果:
从这次的测试中,我们看出,得到了几乎完美的结果!
5. 总结
对于PID参数调节,认准3个点:
P:大力出奇迹
I:消除持续存在的误差
D:“中和”用力过猛,减少波动
作者:An Wenfu
文章来源:TopSemic嵌入式
推荐阅读
欢迎大家点赞留言,更多Arm技术文章动态请关注极术社区嵌入式客栈专栏欢迎添加极术小姐姐微信(id:aijishu20)加入技术交流群,请备注研究方向。