本文特别鸣谢字节跳动 Crane佬解答了我对SWA的疑惑
0 前言
1 Mistral 7B 模型
1.1 SWA(Sliding Window Attention)
2 Mixtral 8x7B(MoE)模型
3 Llama2 70B vs Mixtral 8x7B
0 前言
从前段时间Mistral AI 公司发布全球首款MoE(Mixture-of-Experts)大模型——Mixtral-8x7B 以来,就在AI界引起了不小的轰动,从一众科技自媒体的报道中我注意到了一个关键信息点:比Llama-2 70B具有更少的参数 ,却有更高的精度 。这一点燃起了我的兴趣,故特来学习一下Mixtral 8x7B 相对于Llama 2 70B有何不同。还是老样子
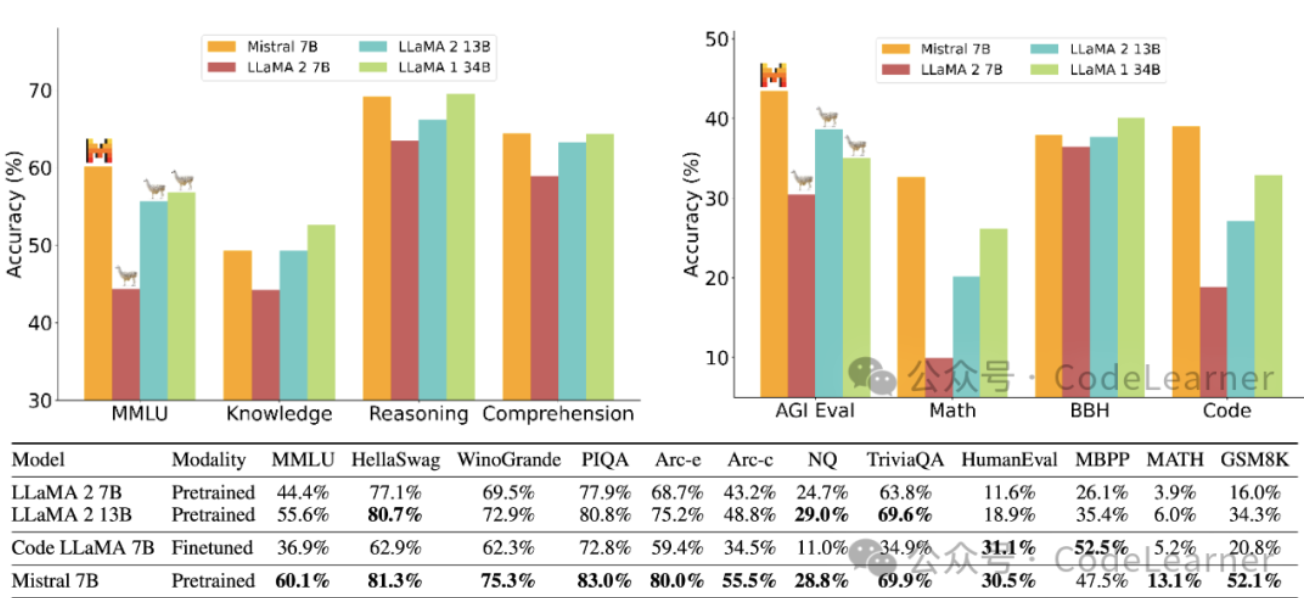
首先,通过Mistral AI 公司的主页我发现他一共发布了两个模型:Mistral 7B 和 Mixtral-8x7B ,后者为基于前者的MoE模型。从其公布的测试结果可以发现Mistral 7B 以7B的参数量在所有benchmarks超越了Llama-2 13B 并且与Llama-2 34B性能相当
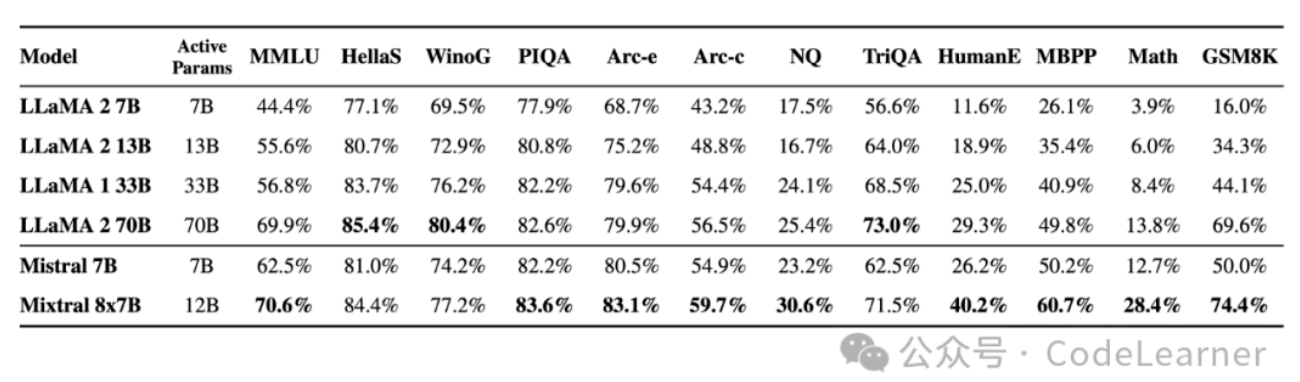
而使用MoE策略的 Mixtral-8x7B 模型则以46.7B参数量,在多数benchmarks上超越Llama 2 70B模型。
如此优异的表现,本文就来看看这两个模型相对于Llama 2做了哪些改变,以及相对于Llama 2 这两个模型的参数量和FLOPs
这里再多说一句,因为Mistral 模型是基于Llama 2模型的,所以对Llama 2模型结构不了解的可以先去看看我之前写的Llama 2详解
1 Mistral 7B模型
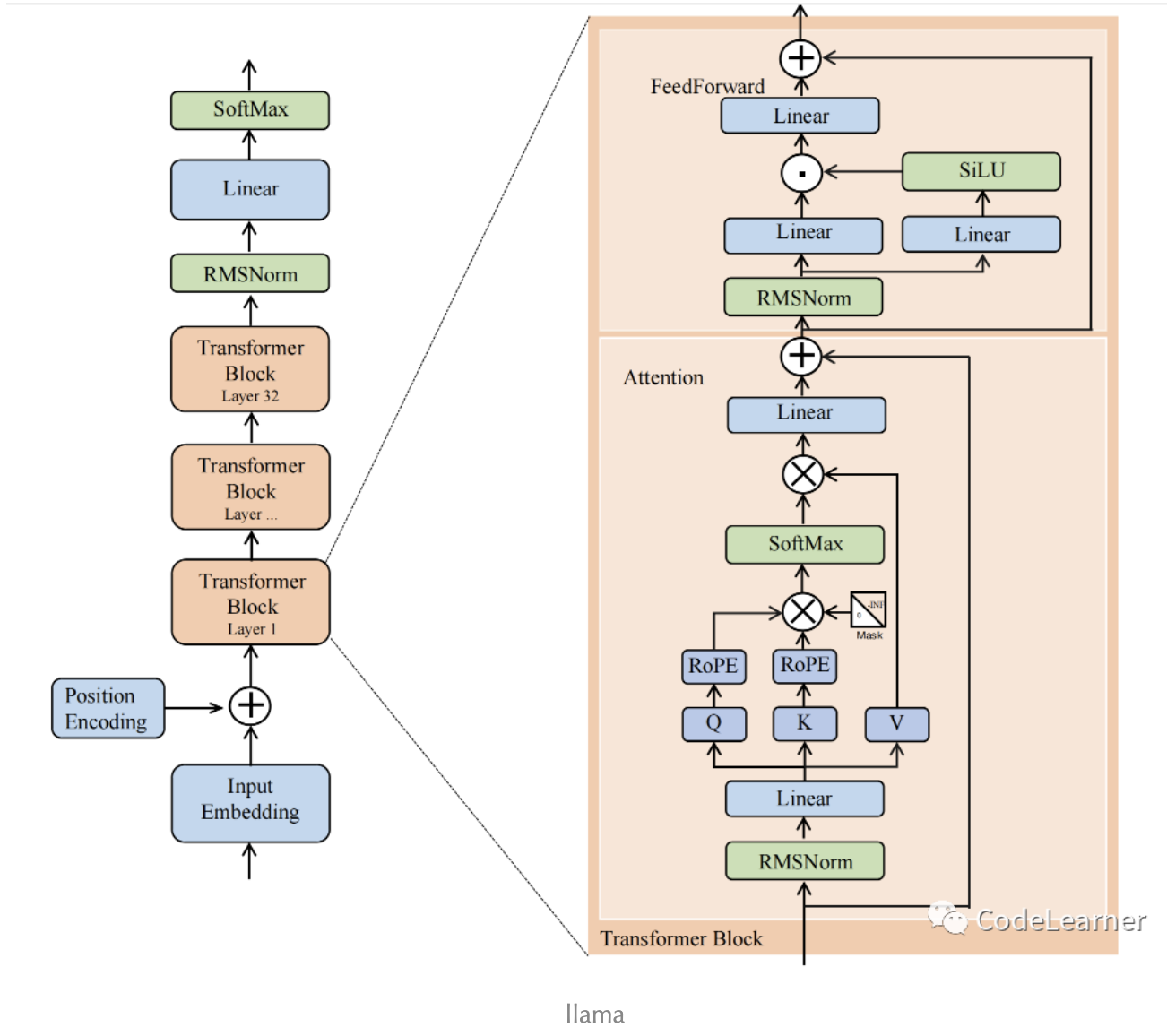
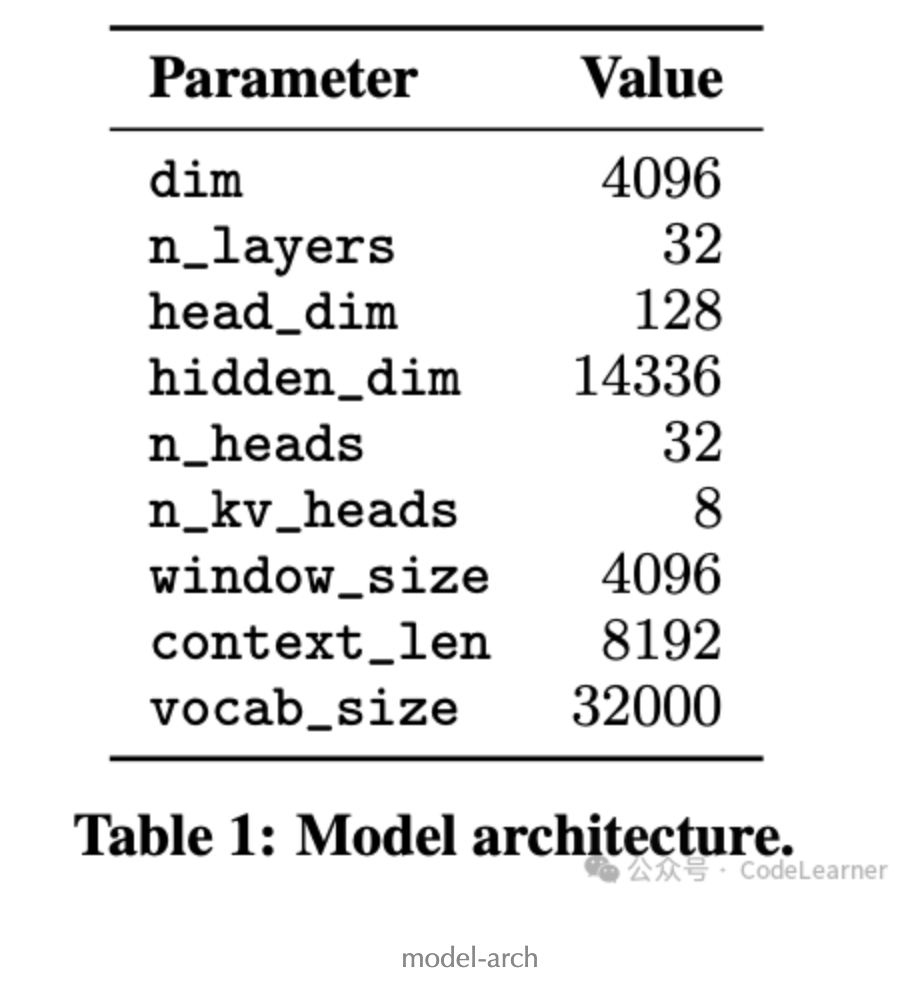
Mistral 7B模型与Llama 2 7B模型结构整体上是相似的,其结构参数如下所示
具体而言,就是存在以下几点差异:
- 对于Attention部分使用GQA (Group Query Attention)来计算注意力机制,其中Q的头数为32,而KV 的头数为8,换句话说就是每4组Q共享一组KV。这一点与Llama 2 不同,Llama 2 是在34B和70B中才使用了GQA,在7B中依然使用的是MHA(Multi-Head-Attention)
- 使用SWA(Sliding Window Attention) 。GQA和SWA叠加来降低显存占用提高推理速度。
- 增大FeedForward HiddenDim的值,由Llama-2 7B的11008 ,改为14336
GQA和更改FFN HiddenDim的值 这两个改动都比较容易理解,那么接下来就主要来看看SWA(Sliding Window Attention)的原理和实现细节
1.1 SWA(Sliding Window Attention)
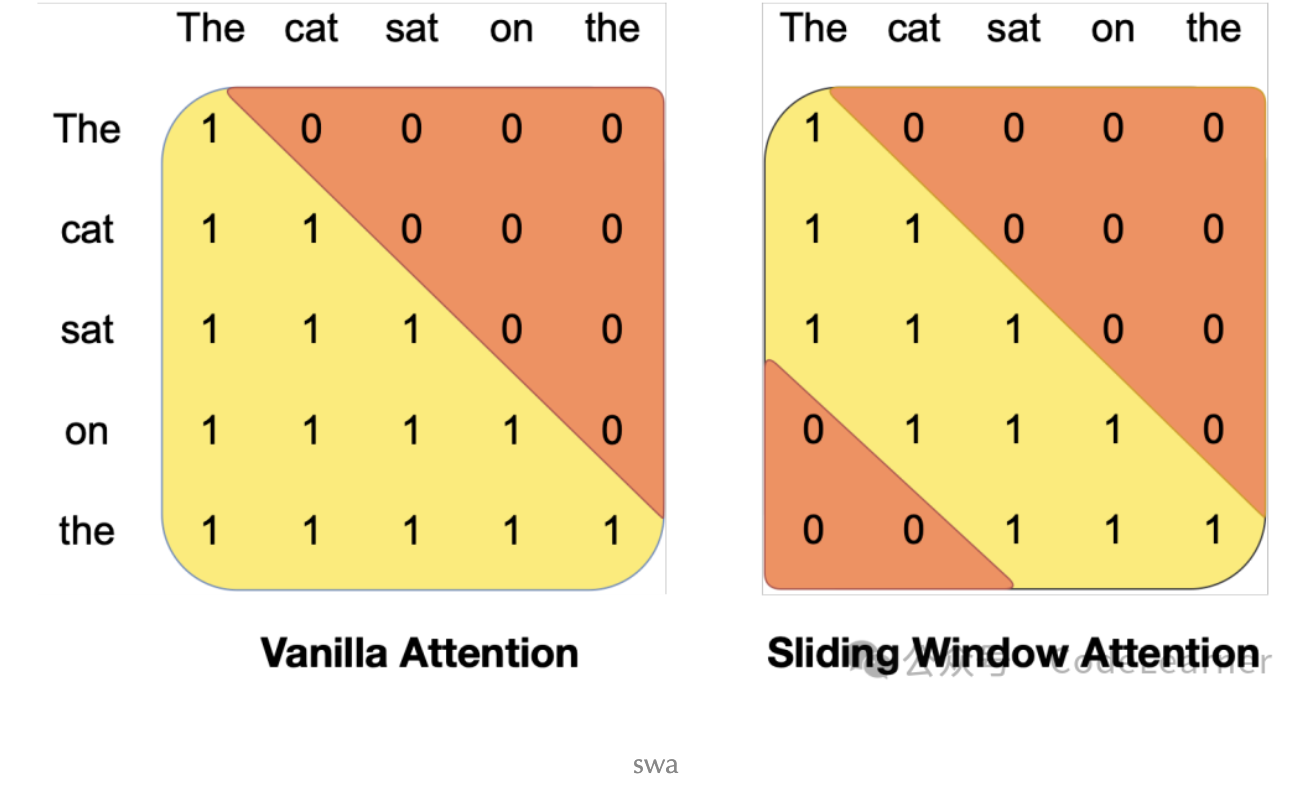
Mistral 使用了GQA和SWA两种方法来加速计算Attention,GQA在Llama 2详解的文章中说明过,这里主要讲解一下SWA。我们知道在Attention的计算一般是Q 与shape为[bst, multi-head,seq_len, head_dim] 的KV进行注意力计算,其中seq_len为已处理所有tokens总数,GQA在多头上做文章使得多组Q共享一组KV;而SWA则是在seq_len这个维度做文章,不在将Q与所有seq-len的KV "直接"计算注意力,而是只与Sliding Window Size个KV"直接"计算注意力,如下示意图,为Sliding Window Size为3的情况
注意:这里用的是直接计算注意力,下文会说明直接的含义
举个例子,在on单词所对应的token计算Attention时,对于普通Attention 可以与前面所有单词对应的 计算Attention,而对于SWA, 只能直接与、、计算。
我们知道在LLM推理时,一般分为prompting 和 generation两个阶段,为了满足SWA,prompting阶段可以通过一个mask的掩码操作实现,如下
if input_ids.shape[1] > 1:
# seqlen推理时在prompt阶段为n,在generation阶段为1
seqlen = input_ids.shape[1]
# mask在推理时也只在prompt阶段有,
#定义一个全1方阵
tensor = torch.full((seqlen, seqlen),fill_value=1)
# 上三角部分全为0
mask = torch.tril(tensor, diagonal=0).to(h.dtype)
# make the mask banded to account for sliding window
# 这里代码diagonal应该等于(-self.args.sliding_window+1)才能满足window size为
# self.args.sliding_window,这应该是官方代码的一个小bug?
mask = torch.triu(mask, diagonal=-self.args.sliding_window)
mask = torch.log(mask)
"""
举个例子,tensor.shape : [10,10]
self.args.sliding_window = 5,则mask为
tensor([[1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 1, 1, 0, 0, 0, 0],
[0, 1, 1, 1, 1, 1, 1, 0, 0, 0],
[0, 0, 1, 1, 1, 1, 1, 1, 0, 0],
[0, 0, 0, 1, 1, 1, 1, 1, 1, 0],
[0, 0, 0, 0, 1, 1, 1, 1, 1, 1]])
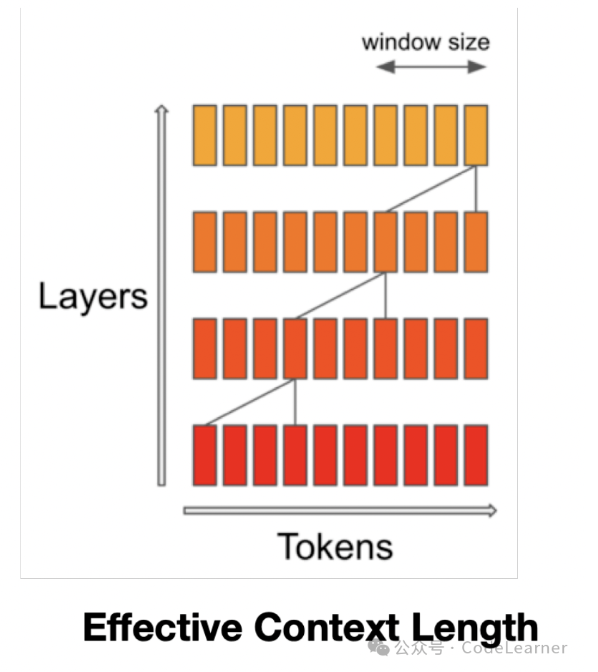
""" 而在generation阶段,因为是自回归生成所以mask起不到作用,那此时mistral则使用了RotatingBufferCache来实现此操作,具体而言,就是采用一种循环右移的存储方式,剔除离得远的KV,保存靠近的KV 。
如上图展示了一个Window Size为4的Cache,循环右移的写Cache的示意图。
RotatingBufferCache代码实现如下
# The cache is a rotating buffer
# positions[-self.sliding_window:] 取最后w个位置的索引,取余
# [None, :, None, None]操作用于扩维度[1,w,1,1]
scatter_pos = (positions[-self.sliding_window:] % self.sliding_window)[None, :, None, None]
# repeat操作repeat维度 [bsz, w, kv_head, head_dim]
scatter_pos = scatter_pos.repeat(bsz, 1, self.n_kv_heads, self.args.head_dim)
# src取[:,-w,:,:] 所以src.shape=[bsz,w,kv_head,head_dim]
# 根据scatter_pos作为index 将src写入cache
self.cache_k[:bsz].scatter_(dim=1, index=scatter_pos, src=xk[:, -self.sliding_window:])
self.cache_v[:bsz].scatter_(dim=1, index=scatter_pos, src=xv[:, -self.sliding_window:]) 我相信多数读者读到这里会跟我有一样的疑问,只让Q与前面Window Size的KV计算Attention,不会影响最终的预测精度吗?因为我们知道当前生成的token是由前面所有token共同决定的。而且论文中并没有特别详细说明,且给出的示意图(下图) 也有些让人费解。
这里结合Crane佬的解答和mistral官方repo的 issuse (https://github.com/mistralai/mistral-src/issues/40),我大概弄明白了:
2 Mixtral 8x7B (MoE)模型
前文说过 Mixtral-8x7B就是Mistral 7B的MoE模型,除了上述Mistral 7B中的特性以外,Mixtral-8x7B还引入了MoE结构。MoE(Mixture-of-Experts) 其实也不是一个新技术,早在1991年就已经被Michael Jordan 和 Geoffrey Hinton所提出 Adaptive mixtures of local experts , 而且关于MoE的发展在深度学习界也从未停止过 (所谓经典永不过时说的便是如此),相关的papers综述这里提供一个写的不错的Blog供大家参考一下:Mixture-of-Experts (MoE) 经典论文一览
这里简单的解释一下什么是MoE,简单点说就是我让一个网络模型结构有多条分支,每条分支代表一个Expert(专家),每个Expert都有其擅长的领域,当具体任务来临时,可以通过一个门空位Gate来具体选择采用哪一个或者哪几个Experts进行计算,这样的好处就是让每个Expert更专注特定领域,降低了不同领域数据对权重学习的干扰。当然在训练MoE模型时也要注意各个Experts负载均衡,防止赢者通吃,达不到想要的目的。
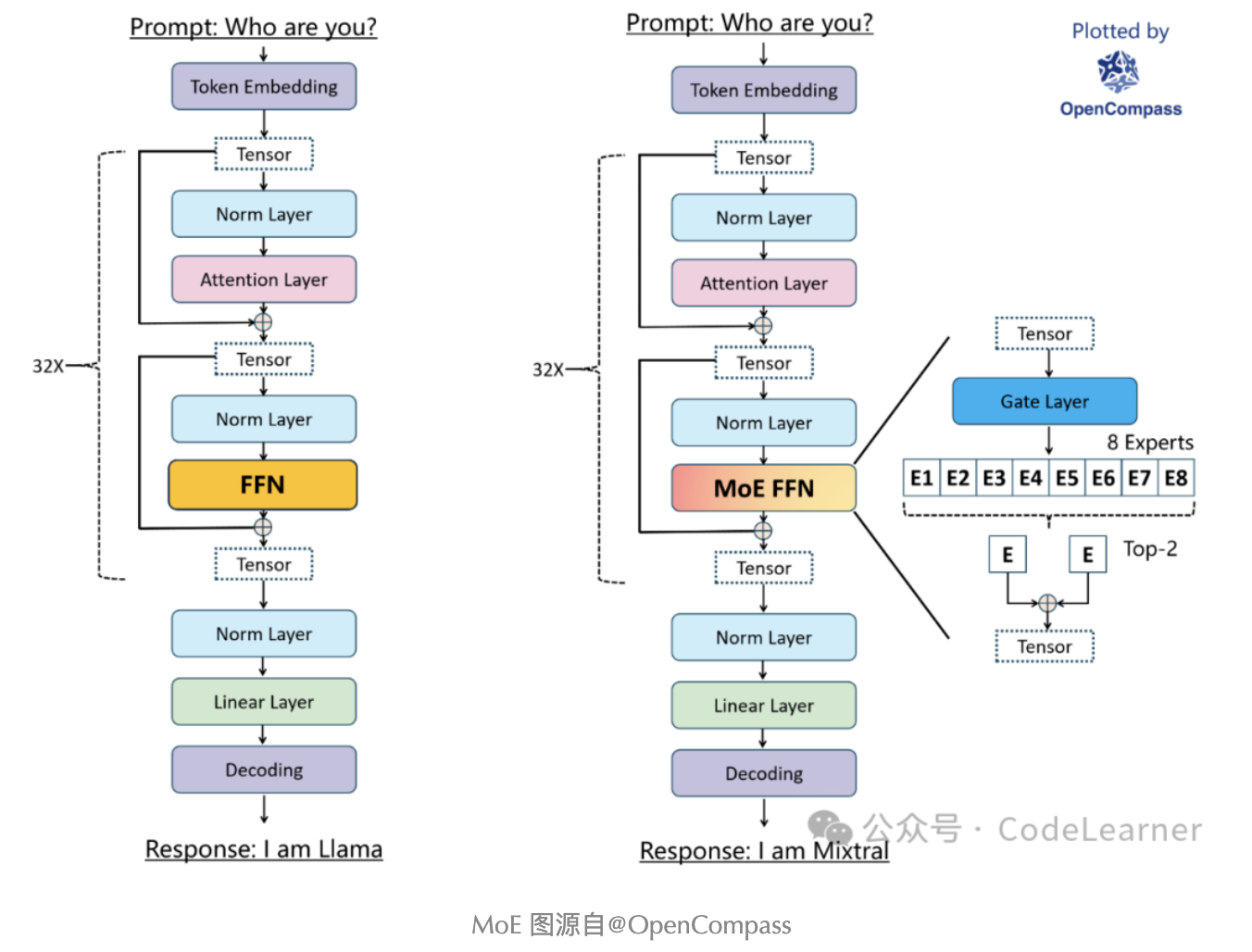
具体到Mixtral 8x7B模型中,其MoE的结构示意图如下所示
可以发现,相对于Llama ,Mixtral 8x7B模型将FFN替换为MoE FFN,还是直接看代码
class MoeLayer(nn.Module):
def __init__(self, experts: List[nn.Module], gate: nn.Module, moe_args: MoeArgs):
super().__init__()
assert len(experts) > 0
# 定义experts,就是一组(8个)Llama FFN,
# Llama FFN就是两个Linear + Silu + Linear
self.experts = nn.ModuleList(experts)
# gate也是一个Linear,这个Linear weight的维度是[hidden_dim , num_experts]
self.gate = gate
self.args = moe_args
def forward(self, inputs: torch.Tensor):
# 更改input shape [bst,seq_len,hidden-dim] -> [bst*seq_len,hidden-dim]
inputs_squashed = inputs.view(-1, inputs.shape[-1])
# Gate Linear 将输入线性映射到num_experts
# 即[bst*seq_len,hidden-dim] -> [bst*seq_len,num_experts]
gate_logits = self.gate(inputs_squashed)
# topk排序
# weights返回topk的值
# selected_experts 返回topk的index
weights, selected_experts = torch.topk(
gate_logits, self.args.num_experts_per_tok
)
# 对每个weight做softmax,归一化
weights = nn.functional.softmax(
weights,
dim=1,
dtype=torch.float,
).type_as(inputs)
results = torch.zeros_like(inputs_squashed)
for i, expert in enumerate(self.experts):
# 根据selected_experts确定weight的行id和列id
batch_idx, nth_expert = torch.where(selected_experts == i)
# 通过上述id选择对应的加权数据 以及执行对应的expert,并将结果加权求和
results[batch_idx] += weights[batch_idx, nth_expert, None] * expert(
inputs_squashed[batch_idx]
)
return results.view_as(inputs) 3 Llama-2 70B vs Mixtral 8x7B
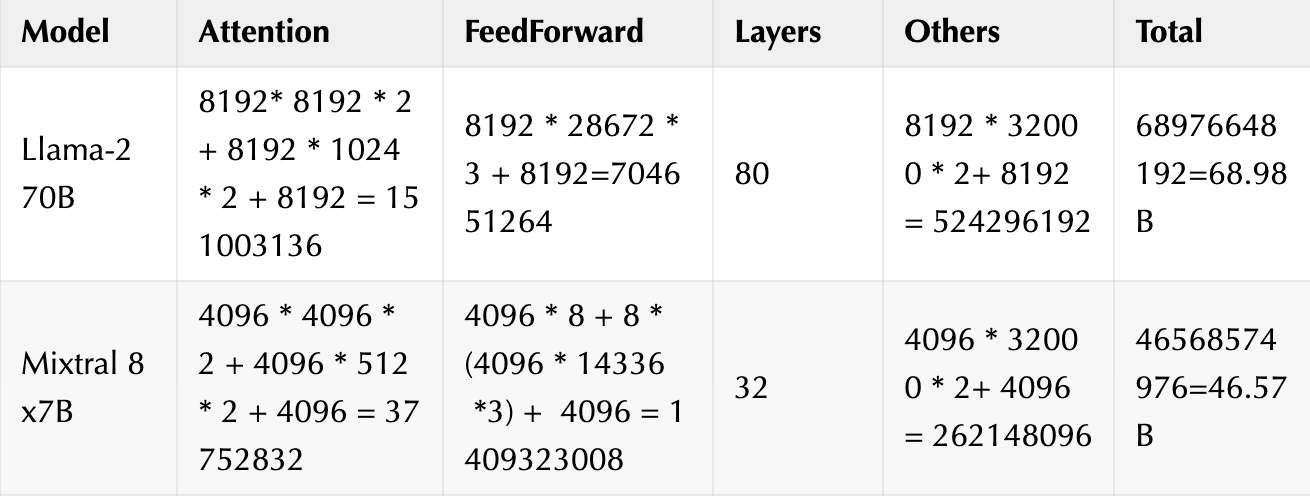
文章的最后,我们再来对比一下Llama-2 70B 和 Mixtral 8x7B 的参数量以及浮点运算量(FLOPs)
- Params
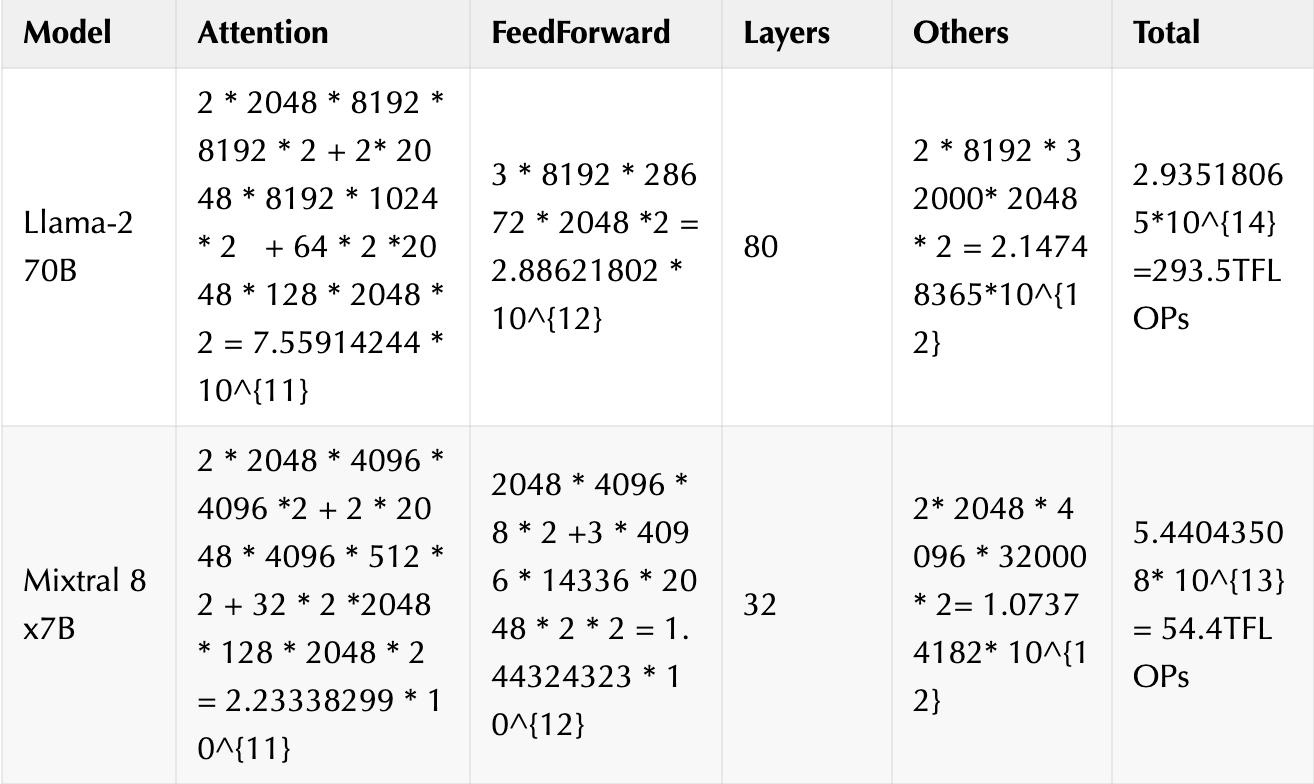
- FLOPs
计算FLOPs,我们就都以输入为2048的单batch作为基准计算,并且我们只计算矩阵乘法相关的FLOPs作为整体网络FLOPs的估算,Norm层的计算先忽略
好啦完结撒花~
作者:CodeLearner
文章来源:CodeLearner
推荐阅读
更多嵌入式AI干货请关注嵌入式AI专栏。欢迎添加极术小姐姐微信(id:aijishu20)加入技术交流群,请备注研究方向。