一、实验目的
了解FIR滤波器的特点,掌握程序算法生成滤波器系数的方法,并实现FIR滤波器滤除高频信号
二、实验原理
FIR滤波器
FIR(Finite Impulse Response)滤波器:有限长单位冲激响应滤波器,又称为非递归型滤波器,是数字信号处理系统中最基本的元件,它可以在保证任意幅频特性的同时具有严格的线性相频特性,同时其单位抽样响应是有限长的,因而滤波器是稳定的系统。因此,FIR滤波器在通信、图像处理、模式识别等领域都有着广泛的应用。
有限脉冲响应(FIR)滤波器(N-1阶),不存在输出对输入的反馈支路,其单位脉冲h(n)是有限长。对于一个FIR滤波器系统,它的冲激响应总是有限长的,其系统函数可记为:

其中,N-1为FIR的滤波器的阶数。
带有常系数的FIR滤波器是一种LTI(线性时不变)数字滤波器。冲激响应是有限的意味着在滤波器中没有发反馈。长度为N的FIR输出对应于输入时间序列x(n)的关系由一种有限卷积和的形式给出,最基本的具体形式如下:

FIR滤波器特性
有限长单位冲激响应(FIR)滤波器有以下特点:
(1)系统的单位冲激响应h (n)在有限个n值处不为零。
(2)系统函数H(z)在|z|>0处收敛,极点全部在z = 0处(因果系统)。
(3)结构上主要是非递归结构,没有输出到输入的反馈,但有些结构中(例如频率抽样结构)也包含有反馈的递归部分。设FIR滤波器的单位冲激响应h (n)为一个N点序列,0 ≤ n ≤N -1,则滤波器的系统函数为:H(z)=∑h(n)* z^(-n),就是说,它有(N-1)阶极点在z = 0处,有(N-1)个零点位于有限z平面的任何位置。
FIR滤波器的设计
FIR滤波器的设计比较简单,就是要设计一个数字滤波器去逼近一个理想的滤波器。通常这个理想的滤波器在频域上是一个矩形窗。
在数字信号处理中,傅里叶变换用来求取时域信号的频率成分。因此,通过对特定频率幅度和相位的响应,求取傅里叶变换的逆变换(IDFT),就可以求出满足要求的数字滤波器。
设计FIR滤波器需要提供的参数:
(1)滤波器的类型:低通、高通、带通、带阻
(2)滤波器的采样频率
(3)滤波器的系数个数
(4)阻带衰减(dB)
(5)通带纹波(dB)
(6)过渡带带宽(Hz)
FIR 滤波器软件实现方法有两种,一种是借助Matlab工具生成滤波器,另外一种是纯算法生成滤波器。本实验中是通过FIR滤波器系数算法生成滤波因子。
算法生成FIR滤波系数
本实验利用Kaiser窗设计一个FIR低通滤波器,有用信号为100Hz,需要滤掉的信号为450Hz。
Kaiser窗是一种应用广泛的可调节窗,它可以通过改变窗函数的形状来控制窗函数旁瓣的大小,从而在设计中可用滤波器的衰减指标来确定窗函数的形状。与其他窗相比,Kaiser窗最大的特点是可以同时调整主瓣和旁瓣宽度。 Kaiser窗的定义如下:

其中n=1,2,⋯,N-1 ,N 表示窗函数的总长度, I_0是第一类贝瑟尔函数。β是一个可调参数,可以通过改变β的值来调整窗函数的形状,从而达到不同的阻带衰减要求。
void filter_coefficient(int n, int band, float fs, float fln, float fhn, float wn, float beta, float h[])
n:滤波器阶数(偶数)
band:滤波器类型,1=低通,2=高通,3=带通,4=带阻
Fs:采样频率
fln:通带上边界频率(低通) 、通带下边界频率(高通、带通、带阻)
fhn:无意义(低通、高通)、通带上边界频率(带通、带阻)
wn:滤波器窗体,1=retangular,2=tapered rectangular,3=triangular,4=Hanning,5=Hamming,6=Blackman,7=Kaiser
beta:Kaiser窗口的β参数(3< β <10)
h:滤波器系数
程序流程设计
设计中首先生成FIR滤波器系数,然后产生带有噪声的原始信号,接着进行FIR滤波,最后截取滤波后有用的信号输出。

数字信号处理库
DSPLIB 包含优化的、C语言可调用的通用信号处理例程,用于计算密集型实时应用程序。 调用这些例程的运行速度比直接用C语言编写的等效代码快得多。使用DSPLIB可以缩短应用程序开发时间。
DSPLIB 3_4_0_0包括适用于 C64x+ 或 C66x 或 C674x 处理器的 Windows 或 Linux 安装可执行文件。 每个可执行文件安装一个组件包存储库、一个文档目录、一个 Eclipse 插件目录和一个扩展的组件目录结构,其中包含组件库、头文件和测试示例。
TMS320C6748处理器使用的是dsplib_c674x_3_4_0_0。
dsplib_c674x_3_4_0_0
将DSPLIB安装到CCS5.5 的安装路径,安装完成后会有相应的文件夹出现。源码所在路径:\dsplib_c674x_3_4_0_0\packages\ti\dsplib\src
函数源码
FIR滤波函数
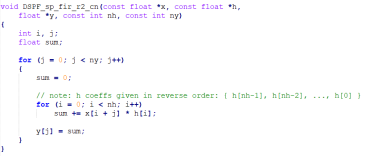
使用DSPLIB 的库来进行FIR滤波。使用时,直接调用“DSPF_sp_fir_r2.h”文件 即可。
API接口
void DSPF_sp_fir_r2(const float x, const float h,float *restrict r, const int nh, const int nr);
三、操作现象
实验设备
本实验所需硬件为实验板、仿真器和电源。

操作现象
硬件连接
(1)连接仿真器和电脑的USB接口。
(2)将拨码开关拨到DEBUG模式01111,连接实验箱电源,拨动电源开关上电。

软件操作
导入工程,选择Demo文件夹下的对应工程
编译工程,生成可执行文件
将CCS连接实验箱并加载程序
程序加载完成后点击运行程序
运行程序后,程序执行完成后会在断点处停下。
接下来通过CCS的图形窗口查看FIR的滤波结果。
先点击 CCS 菜单"Tools->Graph->Single Time",在弹出的界面中设置相关参数,查看原始时域信号+噪声波形。
再次点击 CCS 菜单"Tools->Graph->Single Time",在弹出的界面中设置相关参数,可查看滤波后时域信号波形。
然后点击CCS菜单"Tools->Graph->FFT Magnitude",在弹出的界面中设置相关参数,查看原始频域信号+噪声波形。
再次点击CCS菜单"Tools->Graph->FFT Magnitude",在弹出的界面中设置相关参数,查看滤波后频域信号波形。
对比滤波前后的波形,可知,输入波形中的低频波形通过了滤波器,而高频部分被滤除。
实验结束后,点击红色按钮退出CCS与实验箱的连接,最后实验箱断电即可。



