在多变量数据分析中，涉及三个变量的数据可视化往往需要采用三维绘图技术，以便更全面地理解和分析在二维表示中难以清晰呈现的复杂关系和数据模式。

Python 的 Matplotlib 库通过其 mpl_toolkits.mplot3d 工具包，为复杂三维可视化的生成提供了强大的功能支持。构建三维图形的基础在于正确配置绘图环境以支持三维投影，这需要在绘图坐标轴上进行显式设置。

这一初始化过程对于渲染精确的空间表示和启用高级可视化技术具有关键意义。

实现示例：

 import matplotlib.pyplot as plt  
 fig = plt.figure()  
 ax = plt.axes(projection='3d')  
 plt.show()

输出结果

plt.figure() 函数创建一个新的图形对象，作为所有绘图元素的容器。plt.axes(projection='3d') 向图形添加一组启用了三维投影的坐标轴。其中，projection='3d' 参数明确指定了三维绘图模式。plt.show() 函数负责渲染绘图窗口，最终显示配置好的三维坐标轴系统。

三维线性绘图技术

三维线性绘图，亦称为三维曲线绘制，通过在三维坐标系统内连接数据点来表示连续的空间轨迹。这种可视化技术在描述变量在三个维度上的时间演变或空间变化方面表现出色，使分析人员能够识别在低维表示中难以察觉的数据趋势和变化模式。

在本示例的实现中，采用三角函数（正弦和余弦函数）来生成沿 z 轴方向螺旋上升的参数化曲线，这种方法有效地展示了如何利用周期性函数在三维空间中对循环现象进行数学建模。此类技术在物理学、工程学和计算机图形学等领域得到广泛应用，主要用于可视化物体轨迹、信号处理分析结果以及复杂几何结构的空间关系。

 from mpl_toolkits import mplot3d  
import numpy as np  
import matplotlib.pyplot as plt  
fig = plt.figure()  
ax = plt.axes(projection='3d')  
z = np.linspace(0, 1, 100)  
x = z * np.sin(25 * z)  
y = z * np.cos(25 * z)  
ax.plot3D(x, y, z, 'green')  
ax.set_title('3D Line Plot')  
 plt.show()

输出结果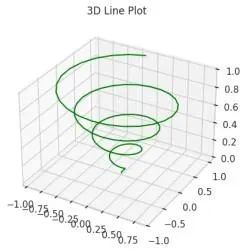

通过 np.linspace() 函数在 0 到 1 的区间内生成 100 个等间距的 z 坐标点，随后计算 x = z × sin(25z) 和 y = z × cos(25z) 来构建螺旋轨迹的参数方程。最终使用 ax.plot3D(x, y, z, 'green') 方法渲染绿色的三维螺旋曲线。

三维散点图可视化

三维散点图是一种专门用于在三维坐标系统中描绘离散数据点的可视化技术。这种方法在识别多变量数据集中的分布模式、发展趋势或数据聚类方面具有显著优势，因为它能够让分析人员直观地观察数据在三个不同维度上的空间分布特征。

在三维散点图中，每个数据点通过一个标记符号（通常为球体或圆点）来表示，其在空间中的位置精确对应于该点的 (x, y, z) 坐标值，从而实现对三个变量的同时可视化分析。

此外，通过引入颜色映射技术（即色彩编码），可以进一步增强可视化效果，将第四个变量（如数据幅度、分类标签或时间序列信息）融入到图形表示中，显著提升图表的分析深度和信息承载能力。这种综合性的可视化方法在科学研究、机器学习算法分析和探索性数据分析等领域应用广泛，特别适用于揭示复杂数据集中的潜在关联关系和异常数据点。

 fig = plt.figure()  
ax = plt.axes(projection='3d')  
z = np.linspace(0, 1, 100)  
x = z * np.sin(25 * z)  
y = z * np.cos(25 * z)  
c = x + y  # 基于 x 和 y 坐标值的颜色映射数组
ax.scatter(x, y, z, c=c)  
ax.set_title('3D Scatter Plot')  
 plt.show()

输出结果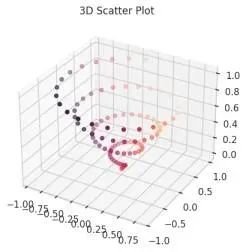

利用与前例相同的 x、y 和 z 坐标数据，通过 ax.scatter() 方法绘制独立的三维散点。颜色参数 c = x + y 的设置实现了基于坐标值的色彩编码，从而引入第四个维度来可视化数据点之间的数值差异。

曲面图可视化技术

曲面图（三维表面可视化）用于描绘在规则 (x, y) 坐标网格上定义的连续参数化表面，其中 z 值决定了表面在垂直方向上的高程分布。这种可视化技术特别适合于表示标量场分布、双变量数学函数（如 f(x,y)）的图形化表示，或者将经验数据集插值到规则网格上的结果可视化。

通过运用颜色渐变和高级着色算法（如 Phong 着色或 Gouraud 着色技术），曲面图能够有效地传达数据的拓扑结构特征，包括局部极值点（峰值和谷值）、地形脊线以及鞍点等关键特征。这使得曲面图在数学分析中的函数研究、地理信息系统中的地形建模，以及计算物理学中偏微分方程解的可视化等应用领域中发挥着不可替代的作用。

 x = np.outer(np.linspace(-2, 2, 10), np.ones(10))  
 y = x.copy().T  
 z = np.cos(x**2 + y**3)  
 fig = plt.figure()  
 ax = plt.axes(projection='3d')  
 ax.plot_surface(x, y, z, cmap='viridis', edgecolor='green')  
 ax.set_title('Surface Plot')  
 plt.show()

输出结果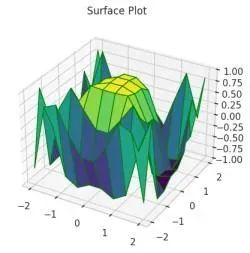

通过 np.outer() 函数结合转置操作 .T 创建 x 和 y 的二维网格矩阵，然后计算 z = cos(x² + y³) 得到表面高程数据。使用 ax.plot_surface() 方法进行曲面可视化，其中 cmap='viridis' 参数指定颜色映射方案，edgecolor='green' 参数设置网格线颜色。

线框图可视化方法

线框图，也称为骨架图或网格图，是一种通过仅渲染表面的边缘和顶点结构、省略面填充来展示曲面几何框架的三维可视化技术。这种简化的三维表面表示方法突出强调了底层的拓扑结构特征，使分析人员能够专注于几何关系的分析、等高线的追踪以及表面网格的连通性研究。

线框图在多个方面表现出独特的技术优势。在拓扑分析方面，它有助于识别关键点（包括局部最大值、最小值和鞍点）并追踪等值线的分布。在可视化透明度方面，线框图允许观察者无障碍地查看表面重叠区域的内部结构。在计算效率方面，相比于完全着色的曲面图，线框图具有更低的渲染计算开销。在数据探索阶段，线框图支持快速迭代分析，特别适用于优先关注结构洞察而非颜色编码数据值的初步可视化分析。

该技术在计算几何、计算机辅助设计和数值分析等领域应用广泛，特别用于偏微分方程解的可视化、参数化表面的展示以及复杂几何模型的结构分析。

 def f(x, y):  
    return np.sin(np.sqrt(x**2 + y**2))  
x = np.linspace(-1, 5, 10)  
y = np.linspace(-1, 5, 10)  
X, Y = np.meshgrid(x, y)  
Z = f(X, Y)  
fig = plt.figure()  
ax = plt.axes(projection='3d')  
ax.plot_wireframe(X, Y, Z, color='green')  
ax.set_title('Wireframe Plot')  
 plt.show()

输出结果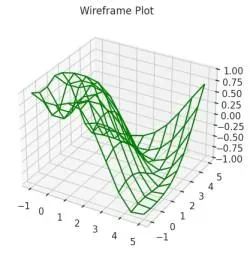

首先定义函数 f(x, y) = sin(√(x² + y²))，然后为 x 和 y 坐标生成网格数据，并计算相应的 z 值。通过 ax.plot_wireframe() 方法将三维表面渲染为绿色线框结构。

三维等高线图技术

三维等高线图是一种将三维表面可视化与投影等高线（等值线）相结合的综合可视化技术，旨在增强对高程梯度和地形特征的空间感知能力。通过将等高线投影叠加到 xy 平面或其他参考平面上，这种方法提供了互补的深度视觉线索，从而强化了表面几何结构的空间表达效果。

这种混合可视化技术能够同时传达多层次的空间信息。在表面形貌方面，通过带有可选颜色映射的着色三维渲染来展示整体地形特征。在等值集合方面，通过追踪等 z 值点形成的等高线来实现类似地形图等值线的效果。在梯度信息方面，通过等高线的空间密度分布来隐式表示坡度变化（等高线间距越小表示地形坡度越陡峭）。

这种可视化方法特别适用于分析标量场分布、数学函数特性或经验数据集的特征，在需要同时理解表面形态和其横截面轮廓特征的应用场景中表现出色。典型应用领域包括地形建模分析、流体动力学研究以及机器学习中的优化问题景观可视化。

 def fun(x, y):  
    return np.sin(np.sqrt(x**2 + y**2))  
x = np.linspace(-10, 10, 40)  
y = np.linspace(-10, 10, 40)  
X, Y = np.meshgrid(x, y)  
Z = fun(X, Y)  
fig = plt.figure(figsize=(10, 8))  
ax = plt.axes(projection='3d')  
ax.plot_surface(X, Y, Z, cmap='cool', alpha=0.8)  
ax.set_title('3D Contour Plot')  
ax.set_xlabel('x')  
ax.set_ylabel('y')  
ax.set_zlabel('z')  
 plt.show()

输出结果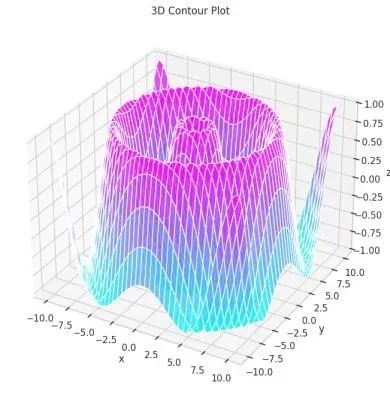

定义函数 fun(x, y) = sin(√(x² + y²)) 并为 x 和 y 坐标生成高密度网格数据。使用 ax.plot_surface() 方法绘制表面，其中 alpha=0.8 参数设置透明度效果，同时添加坐标轴标签以提高图形的可读性和专业性。

E# 表面三角剖分可视化

表面三角剖分可视化技术采用三角网格插值方法（三角剖分算法）从离散数据点构建分段线性的三维表面，无论这些数据点是规则网格排列还是不规则空间分布。三角网格（TIN，即不规则三角网）在处理复杂地形数据方面具有显著的技术优势。

在处理不规则地形方面，三角剖分能够有效建模具有突然间断性的表面，如包含悬崖峭壁或断层结构的复杂地形。在自适应分辨率控制方面，该方法允许在高曲率或数据变异性较大的区域进行更密集的三角剖分，从而实现局部细节的精确表达。在非矩形域处理方面，三角剖分能够处理具有不规则边界或存在缺失值的数据集。在计算效率方面，相比于高阶插值方法，三角剖分显著降低了计算开销。

Delaunay 三角剖分算法通常被用于生成最优网格结构，该算法通过最大化每个三角形的最小角度来最小化数值计算中的伪影效应。这种方法在地理信息系统的数字高程模型构建、计算机图形学的网格渲染以及有限元分析等领域构成了基础性技术支撑。

 frommatplotlib.triimportTriangulation  
deff(x,y):  
    returnnp.sin(np.sqrt(x**2+y**2))  
x=np.linspace(-6,6,30)  
y=np.linspace(-6,6,30)  
X,Y=np.meshgrid(x,y)  
Z=f(X,Y)  
tri=Triangulation(X.ravel(),Y.ravel())  
fig=plt.figure(figsize=(10,8))  
ax=fig.add_subplot(111,projection='3d')  
ax.plot_trisurf(tri,Z.ravel(),cmap='cool',edgecolor='none',alpha=0.8)  
ax.set_title('Surface Triangulation Plot')  
ax.set_xlabel('x')  
ax.set_ylabel('y')  
ax.set_zlabel('z')  
 plt.show()

输出结果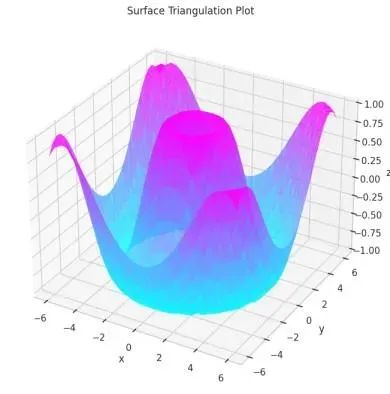

在定义函数并使用 np.meshgrid() 生成 x 和 y 坐标网格后，通过 .ravel() 方法将二维数组展平为一维数组，并创建 Triangulation 对象。使用 ax.plot_trisurf() 方法绘制三角剖分表面，结合颜色映射和透明度设置实现最终的可视化效果。

莫比乌斯带的三维可视化

莫比乌斯带是拓扑学中的一个经典概念，它是一个只有单一表面和单一边界、具有半扭曲结构的几何对象。通过三维可视化技术展示莫比乌斯带的几何形态，能够直观地演示数学理论与视觉艺术的完美结合，同时体现了参数化曲面建模在复杂几何结构表达中的应用价值。

 R = 2  
u = np.linspace(0, 2*np.pi, 100)  
v = np.linspace(-1, 1, 100)  
u, v = np.meshgrid(u, v)  
x = (R + v * np.cos(u / 2)) * np.cos(u)  
y = (R + v * np.cos(u / 2)) * np.sin(u)  
z = v * np.sin(u / 2)  
fig = plt.figure()  
ax = fig.add_subplot(111, projection='3d')  
ax.plot_surface(x, y, z, alpha=0.5)  
ax.set_xlabel('X')  
ax.set_ylabel('Y')  
ax.set_zlabel('Z')  
ax.set_title('Möbius Strip')  
ax.set_xlim([-3, 3])  
ax.set_ylim([-3, 3])  
ax.set_zlim([-3, 3])  
 plt.show()

输出结果

通过生成参数 u 和 v 来分别控制圆周方向和带状宽度的变化范围，然后将其转换为网格形式。利用莫比乌斯带的参数方程计算 x、y 和 z 坐标值，最终通过 ax.plot_surface() 方法结合透明度设置和自定义坐标轴范围来渲染这一具有特殊拓扑性质的扭曲带状结构。

总结

本文详细介绍了 Python 中基于 Matplotlib 库的七种核心三维数据可视化技术，从基础的线性绘图和散点图到高级的曲面建模和三角剖分方法。这些技术为科学计算、数据分析和工程应用中的复杂三维数据可视化提供了完整的技术解决方案。掌握这些可视化方法对于深入理解多维数据的空间关系和内在规律具有重要的实用价值。

https://avoid.overfit.cn/post/a425f209566c4d18baaeffea8474859b