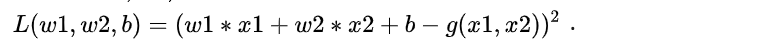《零神经网络实战》系列持续更新介绍神经元怎么工作,最后使用python从0到1不调用神经网络框架(不使用tensorflow等框架)来实现神经网络。从0基础角度进行神经网络实战。本文为第一篇。
首发:https://zhuanlan.zhihu.com/p/59678480
作者:司南牧
目录为:
逻辑与、破除神经元认知障碍、手工调神经元、让计算机自己学习参数、随机梯度下降实践
逻辑与(AND)
我们先不管什么是神经元,咱们先介绍下逻辑与(AND)是什么。在计算机中,存储的是0和1。计算机有很多对这种01操作的运算,其中有一种运算叫做逻辑与,在编程中运算符通常表示为&。两个数进行逻辑与运算的规则就是只要有一个数是0,那么整个运算就是0。还是不太懂?我们举个例子。
1&0 == 0
0&1 == 0
0&0 == 0
1&1 == 1然后我们要解决的问题是,怎么让神经元根据这四组数据自己学习到这种规则。接下来我们整理下这四个数据。然后我们将x1&x2==y的四种情况可以表示为如下所示。我们需要做的是让一个神经元根据这四个数据学习到逻辑与的规则。
x1 x2 y
1 0 0
0 1 0
0 0 0
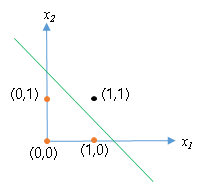
1 1 1也就是说,将(x1,x2)视作一个坐标,将它描点在二维平面是这样的。
我们让神经元能够学习到将(0,1)、(0,0)、(1,0)这些点分类为0,将(1,1)这个点分类为1。更直观的讲就是神经元得是像图中的这条直线一样,将四个点划分成两类。在直线左下是分类为0,直线右上分裂为1.
破除神经元的认知障碍
在人工智能范畴的的神经元它本质是一条直线,这条直线将数据划分为两类。与生物意义上的神经元可谓是千差万别。你可以理解为它是受到生物意义上的神经元启发,然后将它用来形象化数学公式。
既然神经元它在数学意义上就是一条直线那么,怎么表示呢?
学计算机一个很重要的思维就是:任何一个系统都是由输入、输出、和处理组成。
我们在了解神经元也是一样,在本文中的需求是知道一个坐标(x1,x2),输出这个坐标的分类y。
我们按照计算机的输入输出思维整理下思路:
输入:x1,x2输出:y处理:自己学习到从x1,x2到y的一种映射方法
我们知道输入输出,并且我们知道它是直线,那么我们就可以描述这个问题了。
我们让神经元能够学习到将(0,1)、(0,0)、(1,0)这些点分类为0,将(1,1)这个点分类为1。更直观的讲就是神经元得是像图中的这条直线一样,将四个点划分成两类。在直线左下是分类为0,直线右上分裂为1.
我们继续看这个图,在直线的右上方是x1&x2==1的情况,即分类为1的情况。在直线左下是x1&x2==0的情况。这个时候就可以用我们高中的知识来解决这个问题了。在高中我们知道一条直线可以表示为ax1+bx2+c=0。由于在神经元里面大家喜欢把x1,x2前面的系数叫做权重(weight),把常数项叫做偏置(bias)。因此一般大家把x前面系数命名为w,把常数项命名为b。这些都是约定俗成,所以大家记忆下就好。在本文中,我用下面这个公式w1 x1+w2 x2+b=0表示图中的那条绿色的直线。
根据高中知识,一条直线将平面划分成两半,它可以用如下方式来描述所划分的两个半平面。
- 左下:w1 x1+w2 x2+b<0,当x1和x2至少有一个是0 的时候。
- 右上:w1 x1+w2 x2+b>0,当x1和x2都是1 的时候。
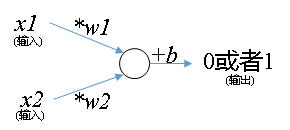
其实w1 x1+w2 x2+b=0,就是神经元,一个公式而已。是不是觉得神经元的神秘感顿时消失?大家平常看到的那种图只不过是受生物启发而画的,用图来描述这个公式而已。我们画个图来表示神经元,这种画图方法是受到生物启发。而求解图中的参数则从来都是数学家早就知道的方法(最小二乘法)。
然后,前面提到过,神经元的形象化是受到生物启发。所以我们先介绍下怎么启发的。
生物意义上的神经元,有突触(输入),有轴突(输出),有细胞核(处理)。并且神经元传输的时候信号只有两个正离子和负离子。这和计算机1和0很类似。
总结下,神经元有突触(输入),有轴突(输出),有细胞核(处理)。开工画图:
咱们把上面这个神经元的数学表达式写一下对比下,w1 x1+w2 x2+b=0.以后啊,大家见到神经元就用这种方式理解就可以。大家不要对神经网络过于迷信化和模糊化,它不是玄学。神经元不是玄学,不是艺术(我只是那种感性经验思维),它是数学和生物启发结合的产物。
好现在我们知道神经元的数学表达和怎么画它的形象化的图了。那么不如我们用编程也表达下它吧?
微信打开:从本质如何理解机器学习
实践:用程序表示一个手工设置权重weight和偏置bias的神经元
去掉注释就10行左右的代码,好现在自己动手实践下吧?计算机思维:动手写代码进行实践是进步的唯一方法
# -*- coding: utf-8 -*-
"""
让神经元学习到逻辑与这个规则
@author: 李韬_varyshare
"""
class Neuron(object):
def __init__(self):
"""
手工设置神经元的权重w_i(输入x_i前面的系数),和偏置常数项b=-1.1
"""
# 初始化权重数组,假定weights[i]和公式中的wi一一对应
self.weights = [1.0,1.0]
# 偏置也初始化为0
self.bias = -1.1
def f(self,x0,x1):
"""
返回值是 weights[0]*x0+weights[1]*x1 + bias > 0? 1:0;
计算这个用于判断(x0,x1)的分类。大于0则是点(x0,x1)在右上输出1,小于0则点在左下输出0;
"""
if self.weights[0]*x0+self.weights[1]*x1 + self.bias > 0:
return 1
else:
return 0
# 哈哈我们手工设置了一个神经元能完美实现逻辑与
n = Neuron()
# 0&1==0
print('0&1=',n.f(0,1))
# 1&0==0
print('1&0=',n.f(1,0))
# 0&0==0
print('0&0=',n.f(0,0))
# 1&1 == 1
print('1&1=',n.f(1,1))
"""
输出:
0&1= 0
1&0= 0
0&0= 0
1&1= 1
"""那么怎么让计算机自己确定神经元的参数?
现在问题来了,现在我们有三个参数w1,w2,b,我们怎么设置这三个参数呢?一个很直观的想法就是自己手动调。
别笑,还真可以。因为我们现在要解决的问题太简单了。一个很直观的解就是只要直线的斜率为-1,即w1=w2=1.然后我们让b=-1.1就可以完美实现逻辑与分类功能。也就是说x1+x2-1.1=0这就是一个符合条件的神经元。
好了,可以洗洗睡散了。
但是,通常我们要解决的问题比这个复杂的多,神经网络是由神经元连接而成。而一般神经网络都是有几百个神经元。假设有200个神经元,我们现在一个神经元有3个参数,那么我们手动需要调200 * 3=600个参数。想想都觉得头皮发麻,而且200个神经元这还算少的,AlphaGo那种级别得上千个。恐怖如斯。
梯度下降
可以看看这个回答初略理解梯度下降:什么是梯度下降法? 。
当然,数学家不会这么傻乎乎的自己手动调。那数学家怎么解决的呢?
现在我们的神经元用公式可以表示为f(x1,x2)=w1 x1+w2 x2+b,现在未知参数是w1,w2,b。那么我们怎么衡量这些未知参数到底等于多少才是最优的呢?
这就得想个办法去量化它对吧。在物理界有个东西叫做误差。我们神经元不就是一个函数f(x1,x2)么,我们要做的是让这个函数尽可能的准确模拟逻辑与(&)这个功能。假设逻辑与(&)可以表示成一个函数g(x1,x2)。那么用物理界的术语,我可以称呼g(x1,x2)为真实值,f(x1,x2)为测量值。真实值和测量值之间的误差可以两者相减并平方来量化。
其实,本文中的g(x1,x2)非常简单。就四个点而已。
x1 x2 g(x1,x2)
1 0 0
0 1 0
0 0 0
1 1 1这样我们就得到了神经元的误差,不同的参数是w1,w2,b对应不同的误差值。这样我们得到了一个误差函数,它的自变量是w1,w2,b。所以问题就转变为了求误差函数最小时,w1,w2,b的取值就是最优的参数。
注意了:误差函数=代价函数=目标函数=损失函数,这三个词可以随意替换的。所以你们在其他地方看到这三个词就都替换成误差函数就可以。别被概念搞蒙了。一定记住误差函数(error)=代价函数(cost function)=目标函数(objective function)=损失函数(loss function)
好是时候表达一波误差函数了,注意误差函数是随w1,w2,b。不同的参数是w1,w2,b对应不同的误差。本文中误差函数可以这么写$$L(w1, w2, b) = ( f(x1,x2) - g(x1,x2))^2$$。然后,现在好像看到右边没有w1,w2,b慌得狠。那么我们快点将f(x1,x2)=w1 x1+w2 x2+b代入写成看得见w1,w2,b的形式。展开后可以写成这个样子:
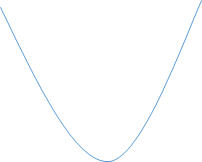
看一看,你觉得它长啥样?如果是只看w1的话,它是个过原点的二次函数。如果综合看w1,w2,它像口锅。如果看w1,w2,b的话,这个维度太高。我等人类想象不出来。
那怎么求L(w1,w2,b)的最小值点呢?注意: 最小值点含有两个意思。一是:我们要求的是自变量w1,w2,b的值,二是函数在这个自变量值取最小值。
再次强调:我们要求的是w1,w2,b的值。因为神经元就是只有这三个未知量,我们不关心其他的。而且在本文中的L(w1,w2,b)
的最小值很明显,它就是0。它是个完全平方嘛肯定>=0。
那怎么求这个误差函数的最小值点呢?
数学家想到了一个办法叫做梯度下降。大家不知道这个方法没关系,现在你需要知道的是梯度下降可以让计算机自动求一个函数最小值时它的自变量值就可以了。注意梯度下降只关心自变量值。不关心函数值。这儿你迷糊也没关系,看到后面回头看这句话就懂了。反正梯度下降它做的事就是找自变量。
接下来咱们一起来学习下啥是梯度下降?啥是梯度?为何下降?梯度下降为了能求得最优参数?
是时候回答前面的“梯度下降”三问了。
- 啥是梯度?梯度就是导数,大家见到“梯度”就把它替换成导数就可以。在多维情况下梯度也是导数只不过是个向量,这个向量每个元素是一个偏导数。
- 为何下降?因为在数学里面(因为神经网络优化本来就是数学问题),在数学里面优化一般只求最小值点。那么有些问题要求最大值点怎么办?答:“在前面加负号”。简单粗暴就解决了。好继续回答为何下降,因为是求最小值点,那么这个函数肯定就像一口锅,我们要找的就是锅底的那个点在哪,然后我们当然要下降才能找到最小值点啦。
- 为何梯度下降能求最优参数?接下来的几段,听我娓娓道来。因为只有知道梯度下降怎么做的,才知道为何它能求最优参数。所以接下来我要介绍的是,梯度下降如何实现利用负梯度进行下降的。
再次总结下,我们需要让计算机求的参数是w1,w2,b. 我们先讲怎么怎使用梯度下降求最优的w1的吧。会求w1其它的几个参数都是一样的求法。
那梯度下降怎么做到求最优的w1呢?(最优指的是误差函数L(w1,w2,b)此时取最小)
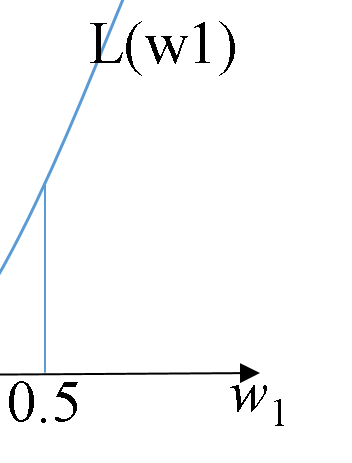
它呀,采取的一个策略是猜。没错,就是猜。简单粗暴。不过它是理性的猜。说的好听点叫做理性的去估计。我们前面提到了误差函数关于w1是一个二次函数,假设长下面这样。
然后计算机它啊,当然不知道长这样啦。它只能看到局部。首先一开始它随便猜,好就猜w1=0.5吧。我们前面提到了计算机它只知道局部。为何呢?你想,我现在取值是w1=0.5,我可以增大一点点或减小一点点w1,这样我当然只知道w1=0.5这周围的误差函数值啦。
现在停下来,花3秒钟,你现在按照你的直觉,w1,你觉得最优的w1到底比0.5大还是比0.5小?
我想我们答案应该是一样的,肯定比0.5小。因为往右边走,即让w1比0.5大的话,它的误差函数是增长的。也就是在w1=0.5周围时候,w1越大,误差越大。
其实梯度下降就是让计算机这么猜,因为计算机判断速度快嘛。猜个上万次就能很容易猜到最优值。
回顾下我们怎么猜的?
我们是直觉上觉得,这个增大w1误差函数是增加的。那么这个怎么用理性思考呢?这个时候就得用到高中老师叫我们的判断函数单调性的方法了。求一阶导数啊,背口诀:“一阶导数>0,函数单调递增,函数值随自变量的增大而增大”。
所以,我们只需要让计算机判断当前猜的这个点导数是大于0还是小于0. 该点一阶导数大于0的话,这个局部是单调递增的,增大w1的值,误差函数值会增大。因此就得减小w1的值;同理,如果一阶导数小于0 ,那么这个局部是单调递减的,我们增大w1的值可以降低误差函数值。
总结规律:
导数>0, 减小w1的值。导数<0,增大w1的值。可以发现,w1的变化与导数符号相反。因此下次要猜的w1的值可以这么表示:下次要猜的w1的值=本次猜的w1的值-导数。有时候导数太大也可能会猜跳的太猛,我们在导数前面乘个小数防止猜的太猛。这个小数大家通常称呼它为学习率。(从这里可以看出学习率肯定小于1的)因此可以这么表示:下次要猜的w1的值=本次猜的w1的值-学习率导数。* 学习率一般设置0.001,0.01,0.03等慢慢增大,如果计算机猜了很久没猜到证明得让它放开步子猜了。就增大它。
现在我们知道梯度下降干嘛了吧,它就是理性的猜最优值。那什么时候结束猜的过程呢?我们看下图,发现它最优值的那个地方导数也是0.那么我们只需要判断误差函数对w1的导数是否接近0就可以。比如它绝对值小于0.01我们就认为已经到了最优点了。
误差函数是这个:$$L(w1, w2, b) = (w1* x1+w2* x2 + b - g(x1,x2))^2$$. 对W1求导,得到导函数$$L'=2(w1* x1+w2* x2+b-g(x1,x2))*x1$$
现在总结下梯度下降(采用的是很常用的随机梯度下降)的步骤:
初始化w1。(随便猜一个数),比如让w1;// 注意了,同样数据反复输入进去训练的次数大家一般叫他epoch,// 大家都这么叫记住就可以,在英语里面epoch=times=次数循环多次(同样的数据重复训练){遍历样本(逐个样本更新参数){ 将样本x1,x2,和标签g(x1,x2),代入损失函数对w1的导函数,求得导数值; 下次要猜的w1的值=本次猜的w1的值-学习率* 导数值;}}然后我们就可以得到最优的w1了。
对于剩下的w2,b他们是一样的,都是利用让计算机猜。大家参考w1怎么求的吧。
注意了,因为我们是二分类问题,虽然我们想让它直接输出0和1,但是很抱歉。它只能输出接近0和接近1的小数。为了方便编程,我们用-1代替0。也就是说只要神经元输出负数我们认为它就是输出0. 因为直接判断它是否接近0和是否接近1编程会更麻烦
注意了,大家以后也会发现很多数据集二分类问题都会用1和-1而不用0.这是为了编程方便。我们只需要判断正负就可以知道是哪个分类。而不是需要判断是接近0还是接近1
注意我们只有下面这四个样本数据:
x1 x2 g(x1,x2)
1 0 -1
0 1 -1
0 0 -1
1 1 1然后我们用伪代码表示下梯度下降求w1,w2,b的值:(10行左右解决随机梯度下降是不是很激动)
# 先随便猜w1,w2,b是多少
w1 = 0.5
w2= 0.8
b = 0.2
#我们设置一个学习率防止猜得太猛,比如跨度太大会从4猜到3,下一步就是从3猜到4
learning_rate = 0.01
do{
for (x1,x2) in 样本集:
# 我们先对各参数求下导数
L关于w1的导数=2*(w1*x1+w2*x2+b-g(x1,x2))*x1
L关于w2的导数=2*(w1*x1+w2*x2+b-g(x1,x2))*x2
L关于b的导数=2*(w1*x1+w2*x2+b-g(x1,x2))
# 接下来是猜各参数的环节
# 下次猜的= 本次猜的 - 学习率*导数
w1 = w1 - learning_rate*L关于w1的导数
w2 = w2 - learning_rate*L关于w2的导数
b = b - learning_rate*L关于b的导数
}while(足够多次数epoch);
# 这样我们就得到了最优的参数了
输出(w1,w2,b)实践:动手实现随机梯度下降(根据上面的那个伪代码)
# -*- coding: utf-8 -*-
"""
让神经元学习到逻辑与这个规则
@author: 李韬_varyshare
"""
# 先随便猜w1,w2,b是多少
w1 = 0.666
w2 = 0.333
b = 0.233
def train():
# 用于训练的数据(四行)一行样本数据格式为 [x1,x2,g(x1,x2)]
data = [
[1, 0, -1],
[0, 1, -1],
[0, 0, -1],
[1, 1, 1]
]
global w1,w2,b # 告诉计算机我修改的是全局变量(每个函数都能修改这个变量)
epoch = 20 # 同样的数据反复训练20次
for _ in range(epoch):
# 逐个样本更新权重
for i in data:
# 这里的i = [x1,x2,g(x1,x2)],它是data中的一行
# 求各自导函数在(x1,x2,g(x1,x2))处的导函数值
d_w1 = 2*(w1*i[0]+w2*i[1]+b-i[2])*i[0]
d_w2 = 2*(w1*i[0]+w2*i[1]+b-i[2])*i[1]
d_b = 2*(w1*i[0]+w2*i[1]+b-i[2])
# 接下来就是愉快的理性猜环节了
# 设置学习率,防止蹦的步子太大
learning_rate = 0.01
# 下次猜的数 = 本次猜的数 - 学习率*导数值
w1_next = w1 - learning_rate*d_w1
w2_next = w2 - learning_rate*d_w2
b_next = b - learning_rate*d_b
# 更新各参数
w1 = w1_next
w2 = w2_next
b = b_next
pass
pass
def f(x1,x2):
"""
这是一个神经元(本质就是一个表达式)
经过训练,我们期望它的返回值是x1&x2
返回值是 w1*x1+w2*x2 + b > 0? 1:0;
计算这个用于判断(x0,x1)的分类。
大于0则是点(x0,x1)在右上输出1,小于0则点在左下输出0;
"""
global w1,w2,b # 告诉计算机我修改的是全局变量(每个函数都能修改这个变量)
if w1*x1+w2*x2 + b > 0:
return 1
else:
return 0
# 我们首先执行下训练,让神经元自己根据四条数据学习逻辑与的规则
train()
# 打印出模型计算出来的三个比较优的参数
print(w1,w2,b)
"""
输出:0.4514297388906616 0.2369025056182418 -0.611635769357402
"""
# 好我们测试下,看神经元有没有自己学习到逻辑与的规则
print("0&1",f(0,1))
print("1&0",f(1,0))
print("0&0",f(0,0))
print("1&1",f(1,1))
"""
输出:
0&1= 0
1&0= 0
0&0= 0
1&1= 1
"""到这里我们已经完成了神经元自己学习逻辑与规则的实践了
github代码下载地址:https://github.com/varyshare/newbie_neural_network_practice/blob/master/neuron_gradient_descent.py
<nr>
欢迎关注我的知乎专栏适合初学者的机器学习神经网络理论到实践。
下一篇为理解并实现反向传播及验证神经网络是否正确