数学与工业,相向而行。
作者 | 火柴Q
编辑 | 甲小姐
分析师 | 丁兆增
趋势与洞见 No.44
1939年9月,二战爆发,纳粹治下的奥地利局势动荡,一位33岁的维也纳人因为“长得像犹太人”,在当年11月遭到一群纳粹党徒攻击。
年底,接到征兵令的这位维也纳人意识到,必须跑路了。他和妻子踏上了一场长途逃亡,先辗转来到莫斯科,再经西伯利亚铁路横跨欧亚大陆,从日本横滨登上了开往大洋彼岸的轮船。1940年3月,终于抵达旧金山的维也纳人心情大好,写信给自家兄弟:旧金山绝对是我见过的最美城市。
不过这还不是旅程的目的地。稍加整顿后,夫妇二人又经太平洋铁路横跨美国,到达了真正的终点——普林斯顿高等研究院。
一趟旅程横跨两个大陆,值了。
更应该感到“值”的是美国。这位33岁的年轻人,就是在入籍仪式当场指出美国宪法漏洞的著名数学家哥德尔。
哥德尔只是当时因战乱移民美国的众多基础科学家之一。
希特勒给罗斯福送上的“大礼”包括但不限于:
爱因斯坦、爱瓦尔德、奥尔、波利亚、德拜、德恩、费勒、费米、冯·诺依曼、弗朗克、佛里德里希、冯卡门、哥德尔、海林格、柯朗、兰德,勒威、纽格堡、诺德海姆、赛格、塔斯基、外尔、魏格纳……
没有这群天才,盟军破解纳粹密码的进程不会那么快;美国也可能没法这么快完成曼哈顿计划,投下一锤定音的原子弹。
更深远的影响发生在战后。
40年代,费米设计建造了世界上第一个核反应堆芝加哥1号,奠定了日后核电产业的基础;50年代,冯·诺依曼帮助IBM第二任掌门人小沃森完成了第一套存储程序计算机701的开发,开启了美国制霸电子信息技术的辉煌;同一时期,战后从英国移民而来的晶体管共同发明人肖克利创立了仙童半导体,该团队的骨干诺伊斯、摩尔等人后来出走,创立了另一巨头英特尔。
此后,在科技上长于应用而弱于基础的“二流暴发户”美国一把翻身。
美国普林斯顿高等研究院成了基础科学的圣殿,全球顶尖人才开始源源不断涌入这个国家——这是美国近80年来高速发展的最大护城河。
大国崛起,必然伴随着基础科学的崛起。
80年轮回,又一个风云变幻、高压弥漫的时刻。
过去数十年,迅猛发展的金融和信息全球化,已使大型跨国公司及其代表的工业界日益成为重要的权力实体,站到了新一轮争端的舞台中央。
当地时间 5 月 15 日,美国总统特朗普签署行政命令,将华为加入“出口禁运”实体清单(即美国企业需要获得特别许可才能向华为出口软硬件产品);上周三中国时间深夜,ARM公司也宣布暂停与华为的芯片架构合作。可以预见的是,为争夺国际地位而拿工业界开刀的手法将越发频繁。
由此引发了一系列热点问题——中国企业在芯片、操作系统等底层技术上到底有多依赖美国?华为“备胎”有多强?开源系统会不会也被“禁运”?
然而,更隐秘而重要的竞争还不在应用面,而在基础科学面。
时间仿佛回到了80年前,危难的另一个名词是机会——被“卡脖子”的地球最新“暴发户”,中国,会孕育出一种更重视底层技术和基础科学,以及拥抱、善待顶尖科学人才的新型科技文化吗?
1.任正非的质问
“用物理方法来解决问题已趋近饱和,要重视数学方法的突起。”
——任正非《中国没有创新土壤,不开放就是死亡》从很多迹象看,中国确实越来越重视基础科学了,尤其重视向来被认为是科学皇后的数学。
令人耳目一新的是,这一次,发出支持声的最强音来自工业界。
相信很多人都已读完了任正非于5月21日接受媒体采访的2万字实录。74岁的任正非在回答中27次提及了“数学”,例举了诸多数学对于华为的重要性:
华为5G标准是源于十多年前土耳其Arikan教授的一篇数学论文;P30手机的照相功能依赖数学把微弱的信号还原;如今华为终端每三个月换一代,主要是数学家的贡献。
他掷地有声地质问:
我们国家修桥、修路、修房子……已经习惯了只要砸钱就行。但是芯片砸钱不行,得砸数学家、物理学家、化学家……但是我们有几个人在认真读书?博士论文真知灼见有多少呢?
来源:AP Photo/Vincent Yu
他甚至表示,等自己退休了要找一个好大学,学数学。
这不是任正非第一次提及数学的重要性。
2012年,在任正非与内部专家的一次座谈《中国没有创新土壤,不开放就是死亡》中,他提到:“我认为用物理方法来解决问题已趋近饱和,要重视数学方法的突起。”
2006年以来,华为在俄罗斯和法国这两个传统数学强国建立了数学研究所。今年初,在接受采访时任正非说:这30年,其实我们真正的突破是数学,手机、系统设备是以数学为中心。
按任正非披露的信息,华为现在已有700多名数学家、800多名物理学家、120多名化学家、六七千名基础研究专家。
无独有偶,连向来被视为“拿来主义”大佬的马化腾在上周二被问及贸易争端时也说:“中国已经走到发展前沿,拿来主义的空间越来越少。如果我们不继续在基础研究和关键技术上下苦功,我们的数字经济就是在沙堆上起高楼,难以为继。”
今年两会前,马化腾还曾发表口头预告:腾讯未来要拿出10亿元建立基金,启动“科学探索奖”,支持数学、物理等基础科学的研究。
更早前的2016年,包括马化腾、李彦宏、丁磊、徐小平在内的中国互联网工业界“大佬”组团捐赠了“未来科学大奖”,单项奖金100万美元,承诺连续捐10年。
当被问起捐款原由时,马化腾说:“这么好的事情怎么能没有我?”他希望让数学、生命科学等基础科学领域成为新的时尚。
在上周六刚刚举行的2019年未来论坛·深圳峰会上,深圳市副市长王立新从城市产业发展的角度提到:
大家从最近的形势也看到基础研究对深圳、对中国是非常非常的重要!我们过去讲80年代上大学的时候说:“学好数理化,走遍天下都不怕”。今天我们有必要重提那句口号,就是:“学好数理化,打遍天下都不怕”。
工业界主动示爱数学,看起来朴素直白,背后却经历了充满辛酸泪的九曲十八弯。
要看清“破冰”的来路和去路,或许先要从骄傲的数学讲起。
2.骄傲的数学
“数学家们正把时间浪费在了无意义的‘谜语逗趣’上。”
——牛顿
一群数学博士聚会,常见的调侃是:
“那谁是不是6化了?”
“听说某某6化了?”
“什么?你小子浓眉大眼的,居然也6化了!”
“6化”一梗,源自理工大校MIT,描摹着数学和外部世界若即若离的微妙关系。
在MIT,所有课程都以数字编码,6字打头的是如今最炙手可热的计算机。本来学数学的人,学着学着溜去了计算机,是为“6化”。
能“6化”,说明数学作为科学之母,跨入其他学科并不难;但“6化”成为一种调侃,则反映了数学和其他学科间的距离感。
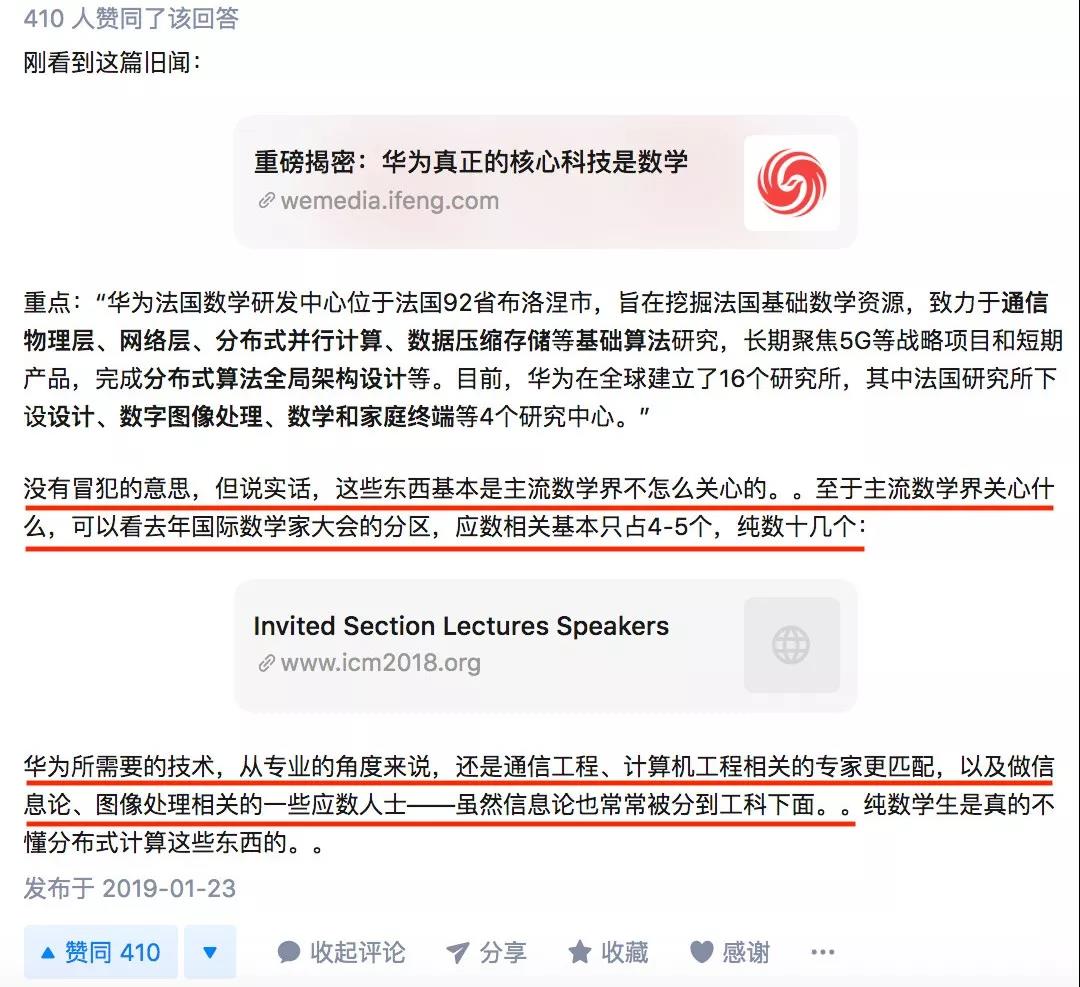
在华为此前建立数学研究中心,并广招数学博士时,也曾遇到过类似的尴尬。
一位快毕业的数学博士在知提乎问:华为为什么要招数学博士?
一个答案是这样的:
答主认为,华为招的其实是应用数学博士,并非“主流数学”,从论文占比来说,纯数才是数学研究的主流。
这个答案引发了激烈的讨论,其中一种极端观点是:应用数学根本不算数学。
为什么理论数学界如此急于对外“划清界限”呢?
这是理论派的骄傲,也是理论派的孤独。
美国数学史家莫里斯·克莱因称这种隔绝为“数学的孤立”。
别误会,数学并非生而骄傲。一开始,数学家们总热衷于解决现实问题:牛顿是因为渴望算出双星轨迹才发明了微积分;庞加莱是为了解决三体问题才发明了微分方程。
曾几何时,璀璨的文艺复兴(14~16世纪)与激荡的大航海时代(15~17世纪)同时上演。数学在与其他学科和各类现实应用的互动中快速发展——航海需要的天体力学、战争中优化炮弹等武器需要的运动力学纷纷刺激、呼唤着数学的新突破。
牛顿引领的科学计算风潮应运而生,在古希腊数学理性、抽象、脱离于自然的传统上注入了对现实的强烈关切,让数学家更关注物理、天文、力学、光学等自然科学和应用中产生的问题,主导了17、18世纪和19世纪大部分时间里的数学文化。而数学也因为与应用紧密交融,带来了丰硕的学术成果。
然而,浪漫的现实主义,却遭遇了漫长岁月里三次数学危机狠狠落下的“锤”:
公元前5世纪,信奉“万物皆数”(整数)的毕达哥拉斯学派慌了:一位叫希伯斯的人发现了一个腰为1的等腰直角三角形的斜边(长度为根号2)永远无法用最简整数比表示,推翻了毕达哥拉斯的著名理论,引发了第一次数学危机。毕达哥拉斯学派愤怒地把希伯斯抛入大海。直到公元前400年,通过对无理数的定义,第一次危机被解决;
18世纪,微积分蓬勃发展,但人们发现牛顿和莱布尼兹分别创立的微积分理论是不严格的,他们对基本概念“无穷小”的理解是混乱的,微积分的合理性遭遇巨大质疑,第二次数学危机爆发。直到柯西用极限的方法定义了“无穷小”,微积分理论才得以进一步发展完善;
19世纪下半叶,康托尔创立了著名的集合论,其干净漂亮让数学家们开始相信集合论可以成为一切数学的基石。1900年的国际数学家大会上,法国著名数学家庞加莱甚至兴高采烈地宣称:“借助集合论概念,我们可以建造整个数学大厦……今天,我们可以说绝对的严格性已经达到了!”
可好景不长。1903年,英国数学家罗素提出著名的“罗素悖论”震惊了数学界:集合论是有漏洞的!第三次数学危机随之爆发。
本意修地基的人,越修却越发现更多的坑。
三次数学危机,让数学家们笃信的数学大厦的严格性一次又一次被撼动、修补、再撼动、再修补,此后,直觉主义、逻辑主义、形式主义和集合论公理化蓬勃发展,被危机吓怕了的数学家深深意识到“攘外必先安内”——四大流派当时的首要任务已不是解决来自物理、天文、光学、航海、炮弹制造等多个实际领域的问题,而是以各自的方式,试图让数学重回一个逻辑严密的系统。
直到1931年,哥德尔终于给了数学体系致命一击。
哥德尔以一篇《论<数学原理>中的形式不可判定命题及有关系统》论文提出“哥德尔不完备定理”——“真的”和“可证的”从此被区分开来,可证的是真的,但真的不一定可证,换句话说,世界上不存在既没有矛盾,又完备的数学系统。
这是一记重锤。数学家们终于开始接受确定性的丧失——数学,并非一个和自然完美对应的真理体系。
咔嚓一下,支撑信念的东西脆裂了。
一种深刻的变化由此蔓延——既然数学并不必然和自然对应,那么用自然中的问题来启发数学研究似乎也并无必要。
此后,自然、现实应用中涌现的问题,不再是指引数学家方向的明灯。
另一方面,现代高校分科制度的建设、教职评定的各种指标,又进一步强化了数学和其他学科之间的分离。学界有学界的规则,全职研究者不得不考虑顶级刊物、奖项的口味。
渐渐地,数学和物理、力学、天文学、电磁学等自然科学的深刻羁绊减弱了,数学被看做“形式科学”,和“自然科学”区隔开来;甚至即使在数学的国度内,数学家们也不再相互理解了。
纯数学变得越发骄傲,失去了牛顿、庞加莱时代的“野蛮”活力(在后世数学家看来,18世纪的数学过于依赖直觉,缺乏严密性)。
1947年,冯·诺依曼曾敏锐地察觉了数学家想抛弃其他试验科学的动向:
在距离经验本源很远的地方,或者在多次“抽象”的近亲繁殖之后,一门数学科学就有退化的风险。起初,数学的风格通常是古典的,一旦它显示出巴洛克式(以装饰繁复著称)的迹象,危险信号就发出来了。
——《数学家》
正如一个孤独的孩子是很难自发变开朗的,改变数学的“孤立”,很难靠从内“自爆”,而需要从外敲击。
比如动荡的二战就是一个敲开数学封闭围墙的钥匙。彼时的普林斯顿高等研究院在“形势所迫”下,成了现代历史上最后一个数学与其他科学紧密互动的殿堂:最杰出的物理学家爱因斯坦、最杰出的数学家哥德尔、开创了计算机科学的冯·诺依曼、人工智能的鼻祖图灵,总能轻松穿过走廊自由交谈,一个世界的智慧启发着另一个世界的方向。
而如今,围墙之外,“6化的世界”又开始急切地敲门了。
3.着急的工业界
“人工智能需要一个坚实的理论基础,否则它的发展会有很大困难。“
——丘成桐
在数学世界的另一端,工业界可没那么深沉。
他们的思维方式简单粗暴——产业发展遇到了瓶颈,亟需更多基础理论支撑。
近年来,从高端制造需要的材料科学,到物流、交通和智慧城市离不开的运筹学,到安全技术所依赖的密码学,再到直接卡住人工智能进展的算法层的思想革新,“硬科技”在工业界的落地,处处呼唤着数学。
去年以来引起中国普通民众关心的半导体产业,正急需数学的贡献。
在芯片设计、制造的繁复流程中,每个微小差别——比如不同的组件尺寸、组件材质、元器件排布等——都可能使芯片性能产生巨大差异,所谓“失之毫厘谬以千里”。
而数学的引入,则能在仿真和模拟环节代替成本高、耗时长的真实实验,提前预判芯片的效果。
目前,科学家已找到了许多描述半导体特性的数学方程,但是在求得精确解上,数学家仍束手无策,只能借由计算机得到近似解。随着芯片制造难度的升级,工业界急需找到更优的计算方法。
在对新型燃料电池、高端装备、高端制造影响深远的材料科学领域,科学家也在呼唤数学家的跨学科援助。
如离散几何分析极有可能助力对纳米多孔材料的研究,这一材料在研发新型催化剂上有广泛的应用前景,而新型催化剂又有可能攻克氢燃料电池的应用难题,从而带来新一轮的汽车革命。
而如今大热的人工智能领域,数学缺席的瓶颈感格外明显。
业界对过去一年的人工智能有一个评价:2018年,人工智能的进展就是没有进展。
《浪潮之巅》作者、硅谷风险投资人吴军有一个判断:“人工智能技术20年内不会有大突破,因为今天的人工智能已经用光了40年来所积累的技术红利。”
这要追溯到神经网络、深度学习方法的缘起。上世纪70年代,计算机科学家就开始研究神经网络在推进人工智能上的可行性。
在《甲小姐对话特伦斯》一文中我们曾提到,当时,人工智能开山鼻祖之一马文·明斯基认为神经网络有数学上的局限性,在他的权威震慑下,神经网络在此后近40年里一直无缘主流。
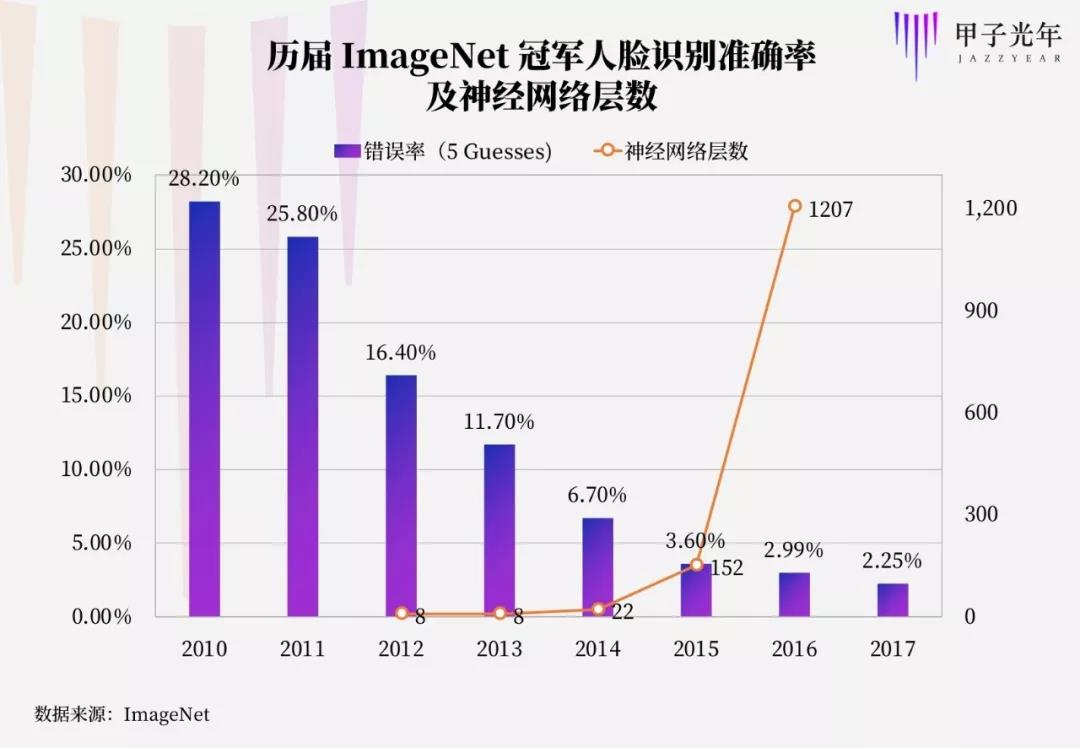
2012年之后,主流快速翻转,深度学习在“大算力+大数据”加持下获得神速进展,功能主义取代理论体系成为人工智能领域的尚方宝剑,但花开遍地后,却遇到了能力进一步提升的关卡。
关卡背后的深层原因是,神经网络和深度学习,是对以逻辑、规则为基础的“建制派”的颠覆:好处是在结合大数据之后效果立竿见影;坏处则是深度学习成了一个人们只知其然而不知其所以然的“黑匣子”,效果显著,却缺乏数学理论支持。
到2016年,人工智能领域的顶级赛事ImageNet中的神经网络层数已达到了1207层,工程思维一度盖过科学思维,但要想进一步发挥作用,没有底层理论支撑很难突破。
在2017年的中国计算机大会(CNCC 2017)上,首位华人菲尔兹得主、哈佛大学终身教授丘成桐曾从数学家的角度发出提醒:
人工智能需要一个坚实的理论基础,否则它的发展会有很大困难。
如今,中国工业界对攀登人工智能高地踌躇满志,在应用领域也是“形势一片大好”,诞生了诸多知名的业界公司,但却面临着丘成桐提及的“基础不牢”的隐忧。
上周五接受《经济观察报》采访时,中国科学院院士、清华大学教授张钹提到了中国人工智能领域目前仍长于跟随,不擅拓荒:
我们的从众心理很严重,比如在人工智能领域,深度学习很热,发表论文的作者中几乎70%是华人,但是其他非热门领域,包括不确定性推理、知识表示等几乎没有华人作者。这就是从众扎堆,不愿意去探索“无人区”。
当被问及瓶颈该如何突围时,张钹院士给出了两个方向:“一是数学,二是脑科学。”
何时可以迎来突围?
院士的回答,真诚中有一点无奈:
“很难预计,我们也很着急。”
4.知其所以然
“数学的核心是解决‘知其然和知其所以然’的问题。”
——华为技术战略部部长朱广平
数学究竟能为工业带来什么?
任正非在采访中提到,F22隐形飞机的隐形原理是五十年代俄罗斯数学家发明的。而华为在2008年推出的传奇技术方案SingleRAN,更是数学支撑工业应用的一个经典范例。
对华为的客户,即网络运营商们来说,SingleRAN解决了一个刚需:在2G、3G、4G和不断到来的通信网络迭代中,提供同时运营多制式网络的能力,从而让运营商以更低成本平滑进入4G时代。
这一方案迅速引领业界风潮,到2010年底,华为已在全球部署了80个SingleRAN网络。《经济学人》的一篇报道提到,拉美运营商AméricaMóvil在部署了华为的SingleRAN之后,基站功耗降低了50%,设备数量减少了70%。
SingleRAN的革新性,离不开背后复杂的数学算法。
2006年,陆家嘴软件园,华为上海研究所903实验室里,射频领域首席专家,华为Fellow吕劲松向多载波技术这一业界难题发起挑战,这是SingleRAN的起点。
在1年半的研发过程中,华为俄罗斯研究所的算法专家鼎力相助——当年华为之所以在莫斯科建俄罗斯研发中心,正是看中了俄罗斯作为传统数学强国的深厚底蕴。
不仅提前布局基础数学研究,华为还通过长年投入,趟完了从基础数学到工程化落地的各种坑。吕劲松在开发多载波技术时,曾在生产线上待了6个月,从库房到物料,到贴片机,清查了各环节可能影响质量的所有细节,保证了SingleRAN的质量。
正是对基础研究的持续投入和超强的工程能力,为华为建立了作为设备商的技术壁垒。借助SingleRAN,此前通信设备业务收入排名全球第四的华为力压爱立信、诺基亚、西门子,在4G普及的2014年,一跃登上世界头把交椅。
5G时代,数学又帮华为进一步获得了制定标准的先机。
去年7月26日,华为深圳总部红毯铺地,欢迎一个神秘来宾,他并非政要商要,而是土耳其毕尔肯大学教授Erdal Arikan。
当天的活动是为了感谢这位非华为编制的研究者。
2010年,已投入5G研发两年的华为发现了Arikan在2008年提出的Polar Code(极化码)理论。
相比Arikan的导师Robert G. Gallager(香农的学生)在1963年提出的信道编码技术LDPC码,Polar Code有理论上的优势,但从工程学的角度来说不成熟。
华为顶着风险,陆续围绕Polar Code投入了数千人的研发资源,把Arikan的论文变成了一系列专利和技术,并使之在2016年底成为5G控制信道编码方案——这是中国厂商第一次掌握了国际移动通信标准制定的话语权。
在去年那场感谢Arikan教授的活动中,任正非说:“我们要加强基础研究的投资,希望用于基础研究费用从每年总研发费用150-200亿美金中划出更多的一块来,例如20%-30%,这样每年有30-40亿美金左右作为基础研究投入。”
这也是为什么,在如今华为遭遇危机后,任正非仍能自信地表态:“华为的5G是绝对不会受影响,在5G技术方面,别的国家两三年内肯定追不上华为。”
2016年获得诺贝尔物理学奖的拓扑绝缘体,也是数学和科学、工业界碰撞的成果。
拓扑学本是数学的一个分支,研究几何体在连续形变中的不变性质。2007年发现的拓扑绝缘体,是将诞生已100多年的拓扑学引入凝聚态物理的成果之一。
拓扑绝缘体被认为是继石墨烯之后的“next big thing”,它内部绝缘,表面导电,特性神奇,在半导体行业极有应用前景。
对拓扑绝缘体做出了贡献的张首晟,在与南洋理工大学学生交流这一发现时提到:爱因斯坦、狄拉克和杨振宁都完美的体现了一种风格——他们都有着最坚定的信念,那就是物理的最基本法则应该是被数学的美感所激发。
而在前沿计算机领域,数学界也显现出兴趣,并开始挑战困扰人工智能已久的深度学习的“黑匣子”问题。
丘成桐及其团队在2017年10月发表了一篇论文,用几何学解释了GAN(生成对抗网络)。
这个成果将GAN与最优传输理论、凸几何进行类比,使其转化为了一个可求解的数学问题,从而为黑箱给出了透明的几何解释——这将有助于设计出更高效、可靠的计算方法。
看来,作为数学泰斗的丘成桐并不在意“6与不6”的界限,这其中有个渊源——丘成桐的学生顾险峰“6化”到了“计算机图形学”,而这种跨界的视角产生了一个如今救人性命的好东西:用于直肠癌筛查的虚拟肠镜。
大多数因筛查及时而获得救治的病人可能很难想象,一切的起源是2000年时,丘成桐办公室里的一块黑板。
在这块黑板上,丘成桐给顾险峰讲了全纯一次微分和黎曼面之间的关系。这些理论后来被顾险峰应用到将直肠曲面摊平展开的想法上,成了虚拟肠景的算法技术核心,这一成果随后被西门子和GE公司购买,目前已是CT扫描器械上的标配软件。
不知不觉间,艰涩的数学支撑起了很多人的平凡“小确幸”。
俄罗斯数学家罗巴切夫斯基曾说:“不管数学的任一分支是多么抽象,总有一天会应用在这实际世界上。 ”
正应了一种说法:所有理论数学,最终都是应用数学。
5.我们终将度过
“一个国家只有数学蓬勃发展,才能展现它国力的强大。数学的发展和至善和国家繁荣昌盛密切相关。 ”
——拿破仑
在80年前的“数学人才大迁徙”中,中国只是全球学术体系的“背景板”——如哥德尔取道日本前往美国时,曾路过日占的满洲里;许多欧洲科学家在横跨美国时经由的太平洋铁路,凝结着150万华人劳工的血泪。
而如今,在数学和工业的最新互动中,中国的“存在感”越来越强。
现在,不仅华为在莫斯科、巴黎建了数学研究中心,支持东欧、日本数学家的研究,各大中国互联网公司也在纷纷硅谷设立实验室,就地招揽人才。
这是一种全球化的“筑巢引凤”。
华为把这一思路表达得很清楚——“在有凤的地方筑巢”,机构跟着人才走,而不是人才跟着机构走。
在全球化体系下,重要的并非地理位置,而是创造价值。从欧洲某个数学家的黑板上,可能会长出新的良药;在中国的某个实验室里,可能正酝酿着推动量子计算前进的发现。
今天,人类的科学技术,比商品经济在世界上的传播交融范围更大、影响更广。
在远古时期,美索不达米亚人建造了巴比伦,印度人发明了十进位制,埃及人建造了金字塔,中国修筑了长城,希腊人擅长逻辑推理,印加人发明了最先进的历法……过往几千年文明史,人类知识的进步,正是千百年来跨地区、跨学科交融互动的累积式发展的结果。
现在,特朗普政府的做法正在动摇科研体系的全球化互动。
从二战时期接收大量欧洲科学家,到战后80年里吸引全球顶尖人才,美国本是这种开放体系的最大受益者。
然而从去年底开始,麻省理工学院、威斯康辛大学、伯克利大学纷纷因“非学术的原因”,宣布不再接受华为捐款。国际主义的筑巢引凤吃了闭门羹:你是大方,我也缺钱(如伯克利这样的公立大学要靠政府拨款,但加州政府财政赤字严重,近年来陆续削减了公立大学的经费),但你的钱,我不能要了。
特朗普政府对美国公司和高校的施压,已产生了一个波及范围远超中美的影响:搞乱了全球分工体系,污染了跨国学术交流。
最坏的不是在边境上筑起高墙,而是在人心里建起提防。
好在,真正理解科技发展背后作用力的人,正选择站在真理的一边。上周四,耶鲁大学校长苏必德的声明在晦暗中带来了些许光亮:
我们坚持欢迎来自世界各地有才干的同事。这丝毫无损于我们对学术诚信的追求……国际学生和学者在耶鲁的校园是受欢迎和尊重的。我们感谢他们在共同追求知识与真理中表现出的专业、创造力和奉献精神;我们申明他们属于耶鲁社区的成员。我在此提示,遇到签证或其他任何问题的国际学生和学者,请联系耶鲁的国际学生和学者办公室。
这位校长很明白:对探索着未知边界的数学家等基础学科先锋来说,提防心尤为有害,它阻挡了人类作为一个整体向前迈进的步伐。
Wir müssen wissen, wir werden wissen.我们必须知道,我们必将知道。
这是1930年,被誉为最后一位“数学全才”的希尔伯特退休时演讲的最后六个单词。彼时,尽管数学家们仍笼罩在第三次数学危机之下,但他们仍然坚信,这幢大厦的基础是坚实的。
但愿这一次,当世界站上门槛,会有更多的人看清科学与工业交汇的价值,和它所需要的朴实根基——一个开放、融合、流动的跨地域、跨学科的人才源泉,一个真正理解进步之含义的文明体系;
但愿这一次,数学不再孤独,工业不再无援,越来越多的人可以基于客观规律抱以同一个信念:
我们必须度过,我们必将度过。
END.
参考资料:
- John Cornwell,Hitler's Scientists: Science, War, and the Devil's Pact,Penguin,2004.09
2.瑞德 著,袁向东,李文林 译,《希尔伯特——数学世界的亚历山大》,上海科学技术出版社,2006.07
- 莫里斯·克莱因 著,李宏魁 译,《数学简史:确定性的消失》,湖岸出版社,2019.03
- 人民邮电报,《华为余承东:GSM/UMTS/LTE是SingleRAN三特性》,2011.02
- 南洋理工大学高等研究所编,《诺贝尔奖得主与名人在新加坡南洋理工大学讲演与访谈》,2016.02
- Na Lei, Kehua Su, Li Cui, Shing-Tung Yau, David Xianfeng Gu,A Geometric View of Optimal Transportation and Generative Model,Computer Aided Geometric Desig,2019.01
- 《光阴的故事》,华为心声社区,2016.10
- 《Fellow吕劲松对话成研:非深潜无以成SE》,华为人,2014.08
- 《超越时代的眼光——为丘成桐先生七十寿辰而作》,老顾谈几何,2019.03
- 西蒙·辛格著,薛密 译,《费马大定理》,2013.01