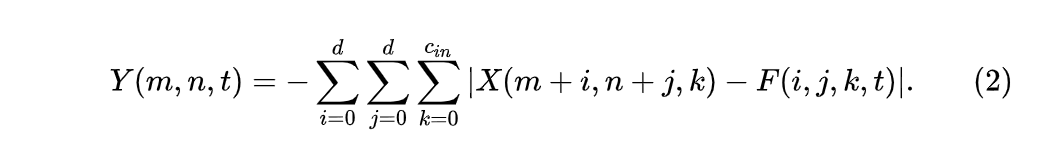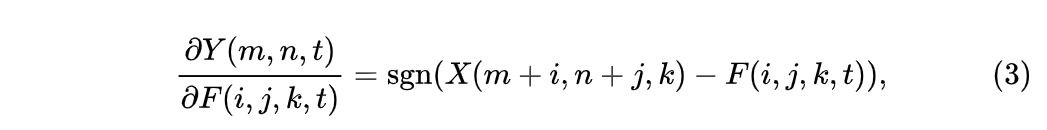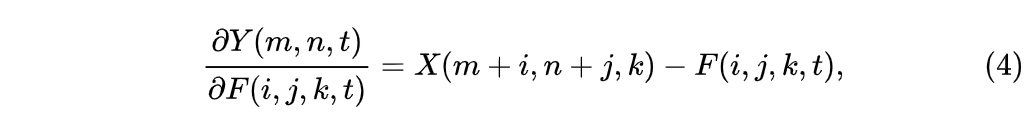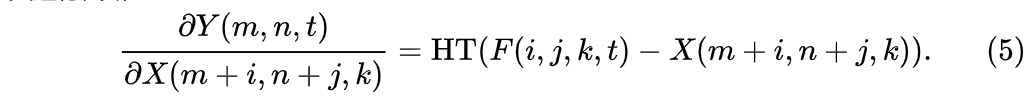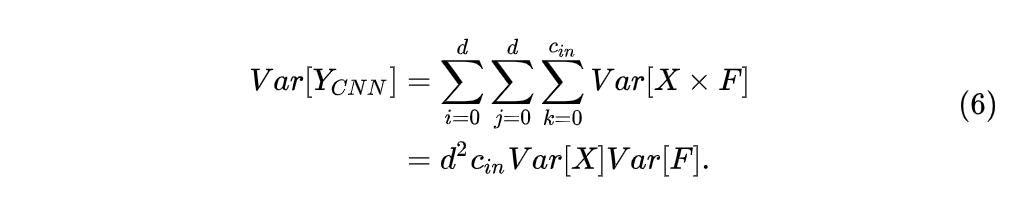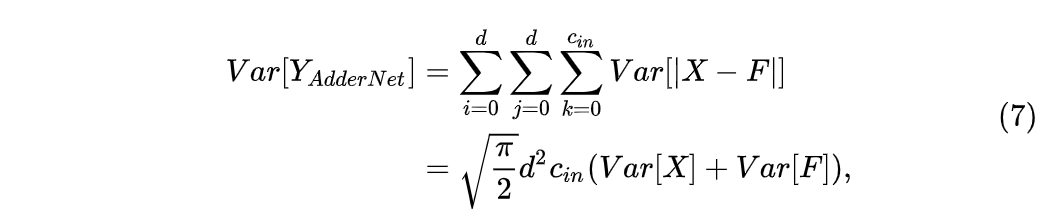华为开源加法神经网络 | CVPR-20 Oral

此前备受大家关注的加法神经网络（AdderNet，ANN）已被CVPR 2020接受，并录用为Oral（接受率约6%）。在这篇工作中，来自北大、华为、悉尼大学的研究员们提出了一种全新的加法神经网络，在ImageNet上使用ResNet-50达到了74.9% 的Top-1准确率和 91.7% 的Top-5的准确率，现已开源。
作者：王云鹤

论文链接：AdderNet: Do We Really Need Multiplications in Deep Learning? （文末提供下载）
开源地址：https://github.com/huawei-noah/AdderNet

引言

深度卷积神经网络在计算机视觉任务中有着广泛的应用。然而由于神经网络常常具有较大的计算量，其无法被直接应用在例如手机、无人车等移动设备上。于是，如何压缩神经网络使得他们可以被应用在资源受限的设备上已成为研究的热点。

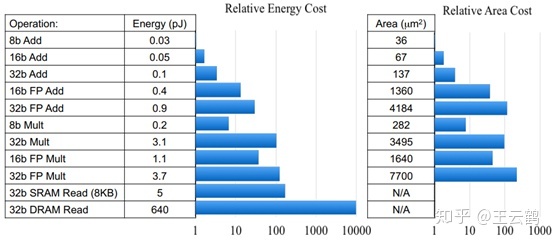
图1：不同比特乘法和加法的运算代价对比

加法，减法，乘法和除法是数学中最基本的四个运算。众所周知，乘法的运算速度比加法慢。图1展示了加法和乘法在45nm元器件上的运算代价，可以看到，乘法的运算代价大大高于加法。然而现有的深度卷积神经网络包含着大量的乘法运算，带来了极大的运算代价。实际上，CNN中的卷积运算是计算特征和卷积核之间的互相关性。卷积被作为看作是从视觉数据中提取特征的默认操作，以往的工作引入各种方法来加速卷积。但是，几乎没有研究者尝试用另一种更有效的相似性度来量代替卷积。由于加法的计算复杂度比乘法低得多。因此，我们研究卷积神经网络中用加法代替乘法的可行性。

在本论文中，我们提出了AdderNet，一种几乎不包含乘法的神经网络。不同于卷积网络，我们使用L1距离来度量神经网络中特征和滤波器之间的相关性。由于L1距离中只包含加法和减法，神经网络中大量的乘法运算可以被替换为加法和减法，从而大大减少了神经网络的计算代价。此外，我们设计了带有自适应学习率的改进的梯度计算方案，以确保滤波器的优化速度和更好的网络收敛。在CIFAR和ImageNet数据集上的结果表明AdderNet可以在分类任务上取得和CNN相似的准确率。

加法神经网络

因此，我们希望使用一种只具有加法的度量函数，即L1距离，来代替卷积神经网络中的卷积计算。通过使用L1距离，输出的特征可以被重新计算为：

可以看到，公式中的计算只需要使用加法，通过将卷积中计算特征的度量方式改为L1距离，我们可以只使用加法来提取神经网络中的特征，并构建加法神经网络。

优化方法

神经网络使用反向传播来计算参数的梯度，再通过梯度下降来对网络中的参数进行优化。在Addernet中，输出特征Y对滤波器F的偏导数为：

其中sgn 代表符号函数。

可以看到，偏导数的输出结果为+1,0或-1，仅有三个值的输出，不能很好的反应输入特征X和滤波器F之间的距离关系，也不利于滤波器的优化。于是，我们考虑将求导公式中的符号函数去掉：

使用改进方式计算的梯度更能表达输入特征和滤波器之间的距离大小关系，也更加有利于梯度的优化，于是我们使用该公式的计算结果来优化滤波器。

特别地，由于使用改进梯度计算出的结果的量级可能大于1，在对输入特征X求偏导数时，我们对其进行截断：

其中HT为HardTanh函数，即将输出截断到-1到+1。如果不对X进行截断，多层的反向传播会使得改进梯度的量级和真实梯度的量级有着很大的累计误差，导致梯度爆炸。

自适应学习率调整

在传统CNN中，我们常常希望每一层之间的输出分布相似，使得网络的计算更加稳定考虑输出特征的方差，我们假设X和F都为均值0的标准正态分布，在CNN中的方差可以被计算为：

通过对卷积核F给定一个很小的方差作为初始化，输出特征Y的方差可以被控制为和输入特征X相似。然而在AdderNet中，输出特征的方差被计算为

可以看到，我们无法给定一个F的方差使得输出特征的方差维持不变，于是输出特征的量级会大大的高于输入的特征，如果不对其进行归一化，将会导致输出的数量级随着网络的深度爆炸。

由于AdderNet的方差很大，计算出的偏导数的量级会很小，于是，AdderNet对滤波器的梯度将会变的很小。

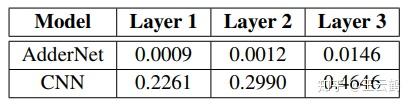
表1：AdderNet和CNN中每层滤波器的梯度大小

表1展示了AdderNet和CNN中滤波器梯度的量级大小，可以看到，AdderNet中滤波器梯度要远远小于CNN，这将十分不利于AdderNet的训练。此外，AdderNet每一层的梯度量级都不一样，因此，我们提出了基于归一化的自适应学习率，以便于AdderNet的训练。具体的，每层的梯度被计算为：

算法1：AdderNet的优化过程

分类结果

我们首先在CIFAR数据集上测试AdderNet的表现，除了CNN以外，由于BNN将神经网络的参数和特征都量化为1比特，其乘法被替换为xnor运算，我们也将BNN作为比较对象。

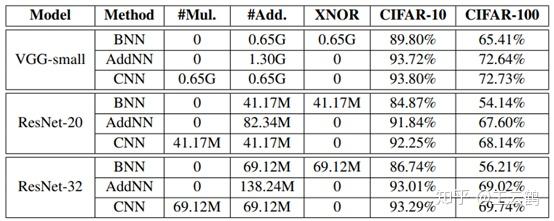
表2：CIFAR数据集上的分类结果

表2展示了AdderNet的分类结果，我们在VGG和ResNet上都进行了测试，结果表明，我们的方法可以取得和正常卷积网络几乎一样的准确率，然而几乎没有乘法（bn层中的乘法数量级远小于卷积层，我们将其忽略），BNN虽然使用更快的XNOR计算，但是其准确率远低于CNN和AdderNet。

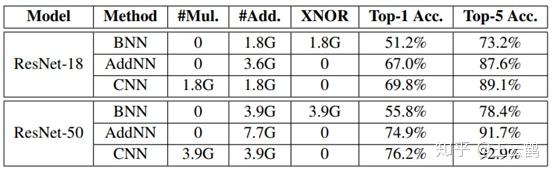
表3：ImageNet分类结果

此外，我们还在ImageNet数据及上进行了实验，可以看到，我们的AdderNet可以在ResNet-50上达到74.9%和91.7%的Top-1和Top-5准确率，非常接近CNN的76.2%和92.9%，证明了AdderNet在大型分类任务上也具有较好的表现。

可视化结果

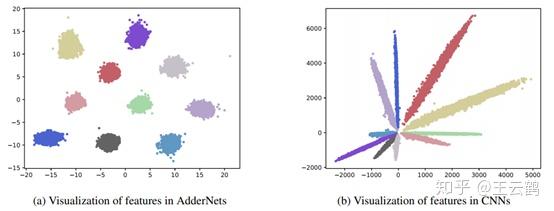
图2：左侧和右侧分别为AdderNet和CNN的特征可视化结果，不同的颜色代表不同类别的图像在网络中的特征。

特征可视化 由于AdderNet使用L1距离来代替了CNN中的互相关性，我们有必要探究其是否能准确地区分不同的类别，图2展示了ANN和CNN的特征可视化，可以看到，CNN使用了互相关性作为特征提取的度量，不同的类别被按照角度分开。而ANN使用的L1距离把不同的类别分成不同的聚类中心，两种方式都可以成功地分开不同类别的图像，证实了ANN可以具有和CNN一样的特征提取能力。

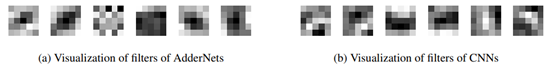
图3：左侧为ANN的滤波器可视化，右侧为CNN的滤波器可视化

滤波器可视化 图3将ANN和CNN的滤波器进行了可视化，可以看到，两种网络虽然采用了不同的度量方式，它们的滤波器都具有较强的纹理特征，都具有提取图片中特征的能力。

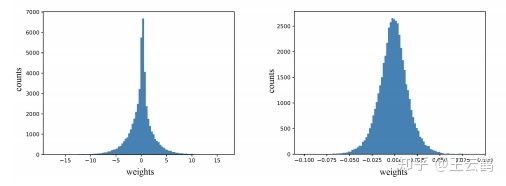
图4：左侧为ANN参数的权重分布，右侧为CNN参数的权重分布。

参数分布可视化 我们还对ANN和CNN中参数的权重分布进行了可视化，可以看到，ANN的参数更接近于拉普拉斯分布，而CNN的权重更接近于正态分布。这也和ANN使用了L1距离作为度量有关。由于L1度量的先验分布为拉普拉斯分布，ANN的参数更倾向于产生拉普拉斯分布。

图5：采用不同优化方法的学习曲线可视化

剥离实验

由于我们对AdderNet提出了特殊的优化方式，我们有必要探究这些优化方法对于AdderNet准确率的影响，我们提出了自适应学习率和更精确的梯度计算方式，从图5可以看到，当采用我们提出的两种方法时（灰色线条），ANN取得了最高的学习率和最小的损失。证明了我们提出的优化方法的有效性。

总结

深度卷积神经网络中包含了大量的乘法，我们探索了将这些乘法用加法替代的可能性。通过使用L1距离来度量特征和卷积核之间的相关性，我们提出了AdderNet，并开发了相应的优化方法。在基准数据集上的实验表明，Addernet可以在几乎没有乘法的情况下取得和相同结构CNN几乎一样的准确率。可视化结果也表明，加法滤波器有望代替原始卷积滤波器用于计算机视觉任务中。在未来的工作中，我们将研究AdderNet的量化，以实现更高的速度和更低的能耗，以及AdderNet在其他计算机视觉任务如检测和分割中的应用。

最后，关于实验细节和开源代码以及一些未来的想法，欢迎大家来github一起讨论。

文章首发知乎，更多深度模型压缩相关的文章请关注深度学习压缩模型论文专栏。