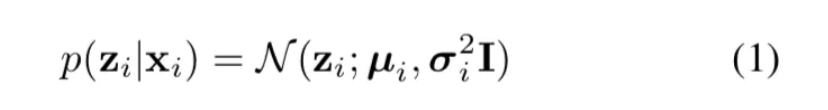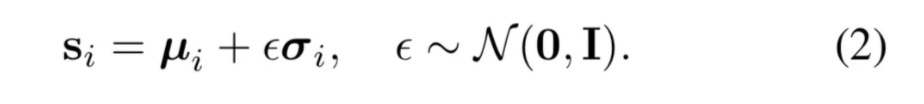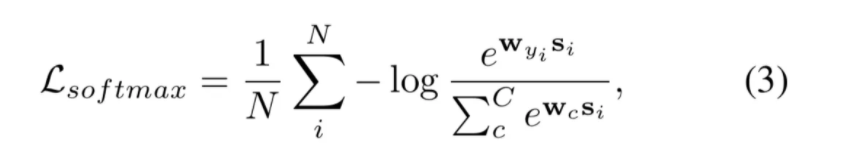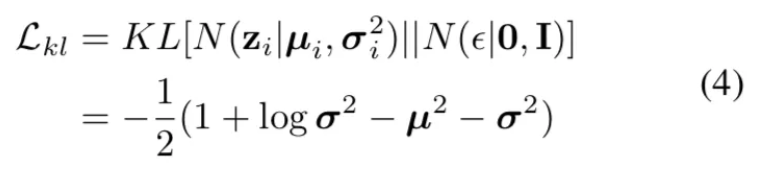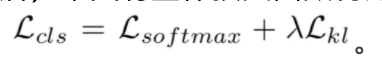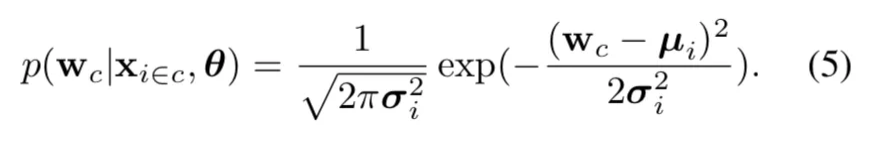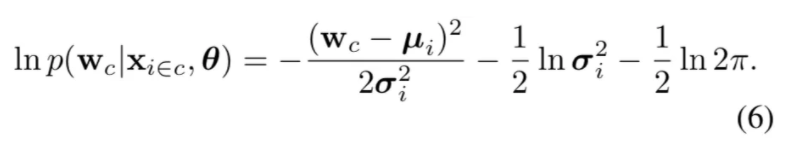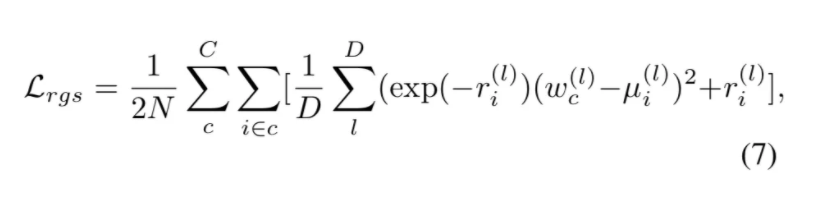本文是旷视CVPR2020论文系列解读第7篇,提出了 Data Uncertainty Learning(DUL)算法,把数据不确定性估计理论应用于人脸识别领域。DUL 算法的两种训练模式可与人脸识别方法的几种主流损失函数有效结合,进一步提升模型在低质量人脸验证和人脸检索任务中的表现。同时,DUL 算法对训练集中的噪声数据具有一定的鲁棒性,可有效缓解脏样本对模型训练产生的不利影响。尤为重要的是,DUL 算法针对每张图像所预测得到的方差,与该张图像的质量呈明显正相关,未来可拓展到无监督学习范式下的视频帧质量推图或高风险人脸验证预警等具体应用方向。
论文名称:Data Uncertainty Learning in Face Recognition
论文链接:https://arxiv.org/abs/2003.11339
导语
数据不确定性(Data uncertainty)来自于数据之内的「噪声」,对于计算机视觉应用而言,比如人脸识别,这种不确定性的建模至关重要,因为噪声广泛存在于图像之中。
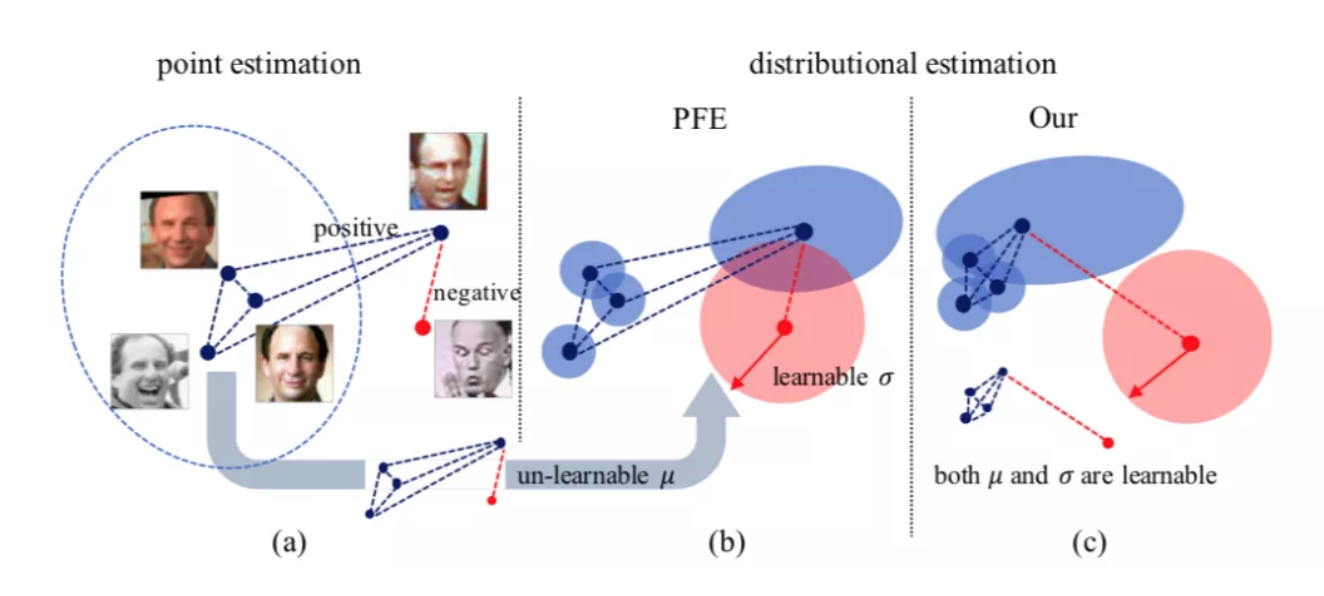
大多数人脸识别方法把每张人脸图像表示为嵌入在隐空间中的一个确定点(deterministic point embedding,即「点嵌入」)。在这种情况下,相同 ID 的高质量图像往往会聚在一起。然而,对于带有噪声的人脸图像,其点嵌入的位置是很难被准确估计的,这就导致该张图像的点嵌入游离在其他同高质量同类样本的点嵌入构成的簇(cluster)之外。换句话说,低质量人脸图片在隐空间的点嵌入具有很大的不确定性。如图1(a)所示。带有一定噪声的正示例与其类别相去甚远,并靠近带有噪声的负示例,造成不匹配。
图1:点估计与分布估计
概率性人脸嵌入(PFE)是人脸识别领域首个考虑数据不确定性的工作。对于每个样本,它估计其在隐空间中的高斯分布(即概率嵌入),而不是一个点嵌入。具体而言,给定一个预训练好的点嵌入 FR 模型,PFE 将每个样本的点嵌入特征视作该样本高斯概率嵌入的均值,并固定住。接着,PFE 在原本的 FR 模型后接入一个新的分支用来预测其高斯概率嵌入的方差。
PFE 的训练损失函数基于一个新的相似性度量,mutual likelihood score(MLS),它可估计两个高斯分布之间的散度。通过优化 MLS 损失,高质量人脸样本的方差会被预测的较小,噪声人脸图像的方差则会被预测的较大。结合 MLS 度量,PFE 可以有效减少噪声样本 1v1 verification 时造成的误匹配问题,如图1(b)所示。
尽管有效,PFE依然有所限制,即在训练过程中,PFE 仅仅优化方差的学习,而不优化原本点嵌入的特征(即均值)。因此,数据不确定性并没有被真正用于影响模型中特征的学习;并且,传统的基于余弦相似性的度量方式无法适用于 PFE 模型。而且,PFE 所依赖的 MLS 度量方式复杂度更高,也更耗内存。
简介
本文首次把数据不确定性学习应用于人脸识别中基于概率嵌入的特征(均值)和不确定性(方差)学习。如图1(c)所示,这一学习方法本质上优化了人脸特征的学习,使得同一类别的实例更聚集,而不同类别的实例更分散。因此,根据本文方法所习得的人脸均值特征可直接与传统的相似性度量适配,无需依赖 MLS 度量方式。
具体而言,本文提出两个学习方法,第一个是基于分类的端到端学习方法;第二个是基于回归的用来优化一个已有模型的方法,类似于 PFE。本文从图像噪声的视角,讨论了上述两种方法中,习得的不确定性是如何影响模型训练过程的。本文给出了 insightful 的结论,即习得的不确定性会自适应性地降低噪声训练样本的反作用,从而提升人脸特征的学习。
方法
本文首先揭示了数据不确定性广泛存在于连续映射空间和与本文任务密切相关的人脸数据集中。接下来,提出了基于分类的方法 DUL\_cls 将数据不确定性引入到标准的人脸分类模型中;同时,也提出另一个基于回归的方法 DUL\_rgs,以提升现有的确定性人脸识别模型。
前言
连续映射空间中的不确定性。假设存在一个连续的 X → Y 的映射空间。其中,每个属于 Y 的 y\_i 被 input-dependent 的噪声,n(x\_i),所腐蚀。x\_i 隶属于 X。那么,这一映射空间本身就携带了数据不确定性。考虑一个简单的情形,即每个 y\_i 所携带的噪声 n(x\_i) 是加性的并且服从一个高斯分布,该高斯分布的均值是0,方差则依赖于 x\_i。
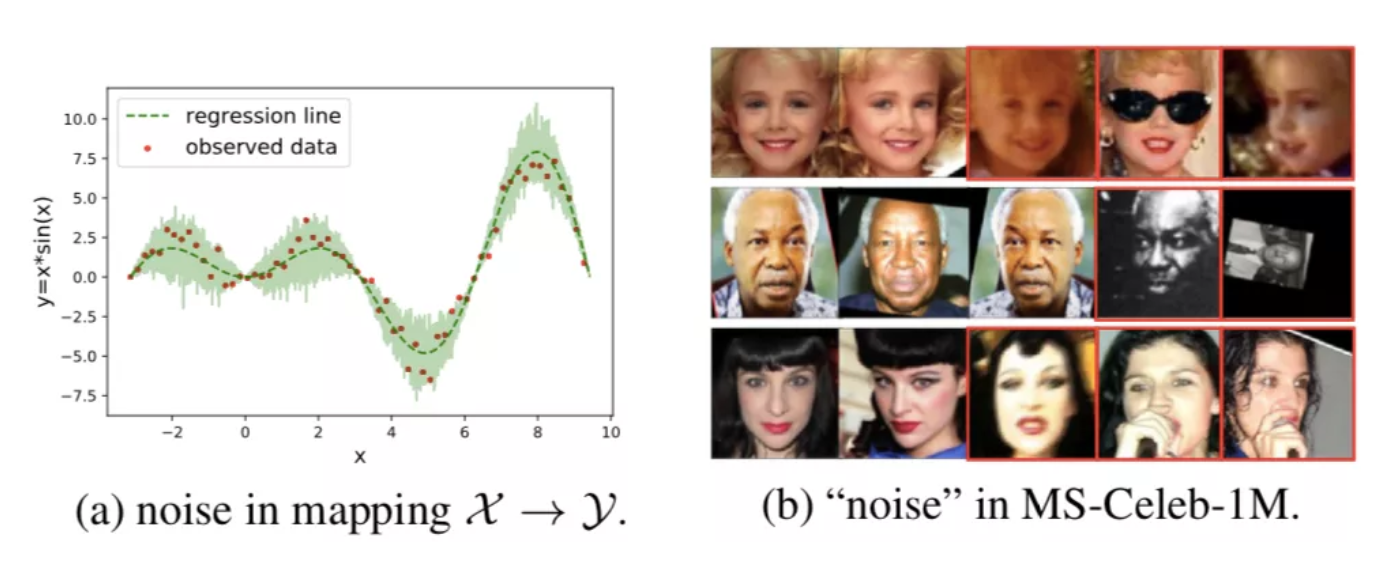
那么,该观察到的连续空间中,y\_i 可表示为:y\_i = _f_(x\_i) + eps*_sigma_(x\_i)。传统的回归模型针对每一个 x\_i,仅仅预测 _f_(x\_i)。但是,带有不确定性估计的回归模型(亦成为异方差不确定性回归)不仅会预测 _f_(x\_i),还预测 _sigma_(x\_i),用来表示对 _f_(x\_i) 这一预测值的不确定性。具体示例见图2(a)。
图2:(a):X → Y映射中的噪声;(b):MS-Celeb-1M中的噪声
人脸数据集中的不确定性。与上文中的连续映射空间类似,人脸数据集也是一个携带数据不确定性的 X → Y 的映射空间,只不过这里 X 是连续的图像空间,Y 则是一个离散的 ID 标签空间。一般而言,海量的人脸数据往往是通过各种途径采集或者爬取而来,因此,有些人脸图像模糊不清,如图2(b)所示。
如上所述,基于深度学习的人脸识别模型往往将一张人脸图像表征为隐空间中的一个点嵌入 z\_i 。假设每个人脸图像 x\_i 存在一个“理想”的嵌入 _f_(x\_i),该嵌入最大程度地表征了该人脸的 ID 信息,并且最小程度地受到该张图片中与 ID 无关的其他信息的干扰。
那么,实际中通过深度学习模型提取的人脸隐特征 z\_i,可以被表示成:z\_i = _f_(x\_i) + _n_(x\_i),其中,n(x\_i) 被视为提取到的与 ID 无关的干扰信息,它对希望获得到的真正人脸 ID 特征 f(x\_i) 构成了「腐蚀」。本文将 n(x\_i) 看为 z\_i 中的不确定性。
基于分类的人脸识别DUL
本部分提出 DUL\_cls 算法,将数据不确定性学习引入端到端的人脸分类模型。
概率化的表征:本文将每个样本 x\_i 在隐空间上的表示 z\_i 定义为一个高斯分布:
其中,高斯分布的两个参数(均值和方差)都是 input-dependent 的,分别由不同的 CNN 分支预测得来。本文将均值特征,μ\_i,视为人脸图片中与 ID 相关的信息,而方差特征,σ\_i,视为对于预测的 μ\_i 的不确定性。
现在,对每一个样本的表示不再是一个确定性的点嵌入,而应该是一个从高斯隐空间分布中采样得到的随机性嵌入。然而,由于采样操作在 CNN 优化过程中不可导,因此它阻碍了模型训练时梯度信息的反传。
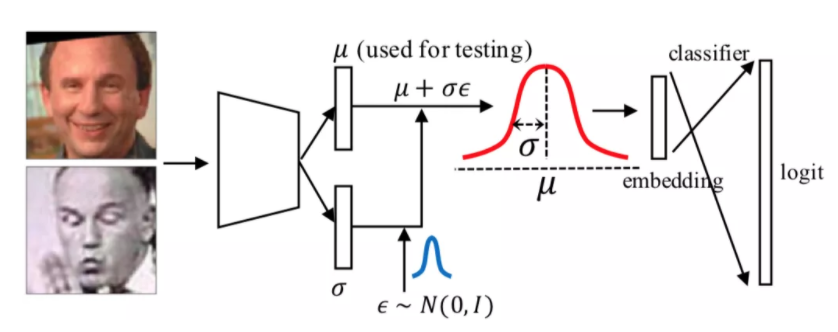
针对这个问题,本文使用参考 VAE 使用了重参技巧。具体而言,首先从标准正态分布中随机采样一个噪声ε,它独立与模型参数之外,然后,本文利用公式2得到等价于采样操作的随机性嵌入表征(整个过程如图3所示):
图3:DUL\_cls模型示意图
分类损失:由于 s\_i 是每张图像 x\_i 的最终表示,将其输入一个分类器,以最小化下方 softmax 损失:
实际使用中,本文采用 softmax 的各种变种,如AMSoftMax,ArcFace,L2SoftMax。
KL散度正则化:由等式2可知,与 ID 信息相关的表征,μ\_i,会在训练期间受到不确定性 σ\_i 的 「腐蚀」。在仅优化该分类损失函数(等式3)时,会出现模式坍塌效应,使得模型对于所有样本的 σ\_i 的预测都偏小,且趋于一个常数,以使得分类损失可以正常收敛。在这种情况下,随机性的嵌入表征可以视为 s\_i = μ\_i + c(其中,c 为一个常数),此时,其实整个模型可以看做“退化”为了原本的确定性嵌入模型。
本文受到变分信息瓶颈理论的启发,在优化过程引入了一个正则化项,约束模型学到的分布 N(μ\_i, σ\_i) 与标准正态分布 N(0,1) 接近。本文利用Kullback-Leibler散度(KLD)度量两个分布之间的「距离」,其数学形式如下:
注意,在 σ\_i 的每一维被限制在(0, 1) 范围内时, 等式4关于 σ\_i 是单调递减的。等式4能对等式3起到很好的平衡作用。具体地,当模型对于所有样本都预测出偏小的 σ 时,L\_kl 损失(等式4)会增大,从而对模型起到乘法作用。反之,当模型对于所有样本都预测出偏大的 σ 时,虽然 L\_kl 整体偏小,但是较大的 σ\_i 会对于 μ\_i 起到严重的“腐蚀”作用,从而使得分类 loss 无法被正常优化。最后,本文将整体损失函数构建为
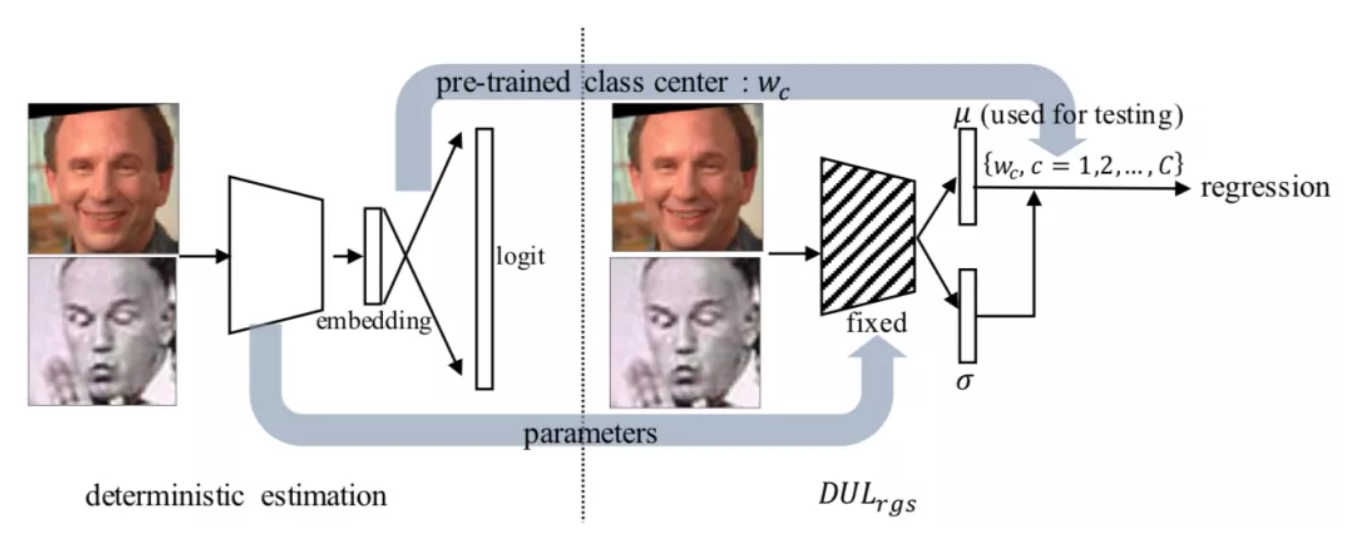
基于回归的人脸识别DUL
DUL\_rgs的提出受到了在连续映射空间中进行异方差不确定性回归(图2,a)的启发。这其中的关键问题是解决人脸识别任务中,Y 空间由离散变量构成,而无法作为一个连续目标向量来逼近的问题(该问题也被 PFE 提及,但是并未被 PFE 解决)。
针对上述困难,本文构建一个新的人脸识别映射空间,它是连续的映射空间,并且最重要的是,它几乎等价于原来离散的目标空间,以保持正确的映射关系。具体而言,本文利用一个 pre-trained 的人脸识别模型,提取其分类层的权重矩阵,W。其中,每个隶属于 W 的 w\_c 可以被视为该类样本的类中心,从而 X → W 便是一个新的连续映射空间。在此基础上,本文可以利用异方差不确定性回归的理论也解决人脸任务中的噪声问题。
概率化的表征:文用数据不确定性回归来估计人脸中 ID 相关的表征 _f_(x\_i)和 不确定性 _n_(x\_i)。
图4:DUL\_rgs模型示意图
如果将每个W\_c都看作目标,那就可以通过最大化下面的似然度来得到每一个X\_i:
实际操作中,本文对这个似然度取了对数:
本文训练神经网络来预测对数的方差,以稳定随机优化过程中的数值,并通过最小化损失函数获取似然度的最大化操作:
对于等式7的「Loss Attenuation」机制的解释可以参考原始论文。
实验
本文给出定性和定量分析以探索习得的数据不确定性的意义,以及数据不确定性学习如何影响人脸模型的学习;MS-Celeb-1M噪声数据集上的实验表明,本文方法比确定性方法更加鲁棒。
对比确定性基准
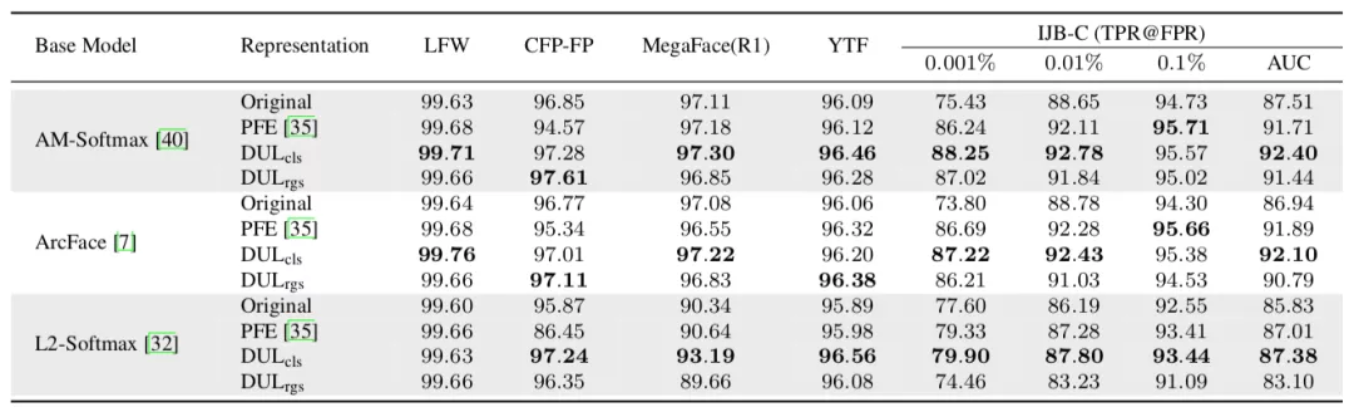
表1:MS-Celeb-1M数据集上的模型(ResNet18)训练结果
表1给出了DUL模型和各种基线模型的测试结果。本文方法在大多数基准上超越基线模型,表明该方法在不同损失函数上的有效性。
这些结果还表明,使用数据不确定性训练的 ID 嵌入相比基线模型估计的点嵌入有着更优的类间聚合性和类内分离性,尤其是在那些根据挑战性的数据集上。
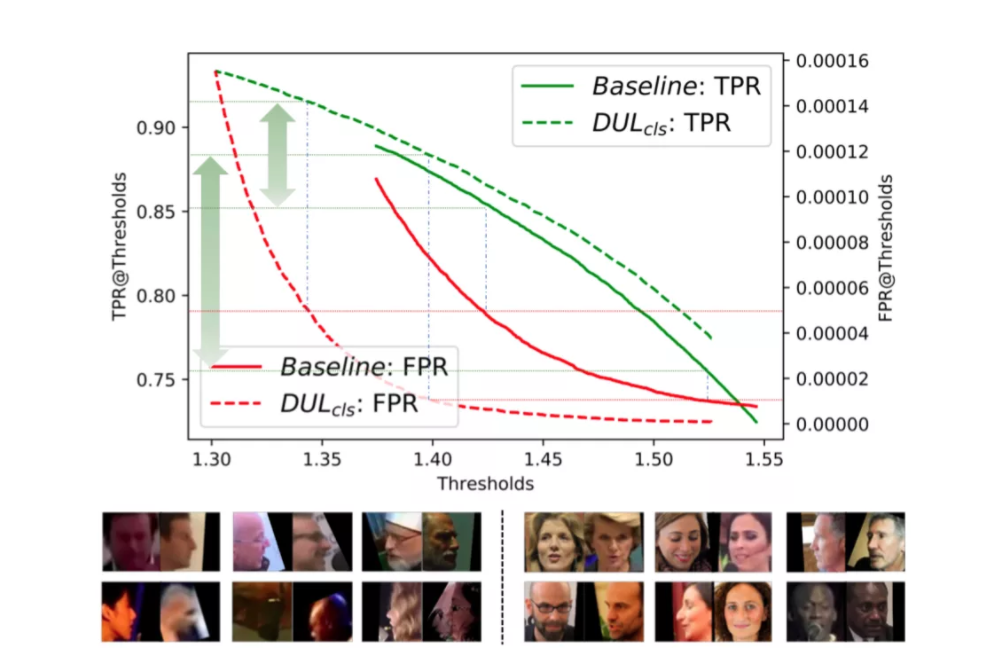
图5:上:TPR&FPR vs. IJB-C阈值;下:基线模型中的FP case(左),DUL\_cls中的 FP case
DUL同样在最具挑战性的IJB-C benchmark上取得最为显著的提升。如图5所示,在不同阈值下,DUL\_cls相较于基线模型,取得了更高的TPR和更低的FPR。图5还给出了在基准模型和DUL\_cls中分别发生的绝大多数错误接受情况。
可以看到,DUL\_cls解决了带有极端噪声的更多的FP情况,这通常发生在基线模型中。这说明,相较于确定性模型,带有数据不确定性学习的模型更适用于不受限的人脸识别场景。DUL\_rgs也得到相似结论。
对比PFE
DUL\_cls/rgs在特征上使用平均池化聚合,并通过余弦相似性进行评估。相较于PFE,DUL\_cls在所有情况中取得了更佳表现,DUL\_rgs也给出了有竞争力的表现。对比结果如表1所示。
对比SOTA
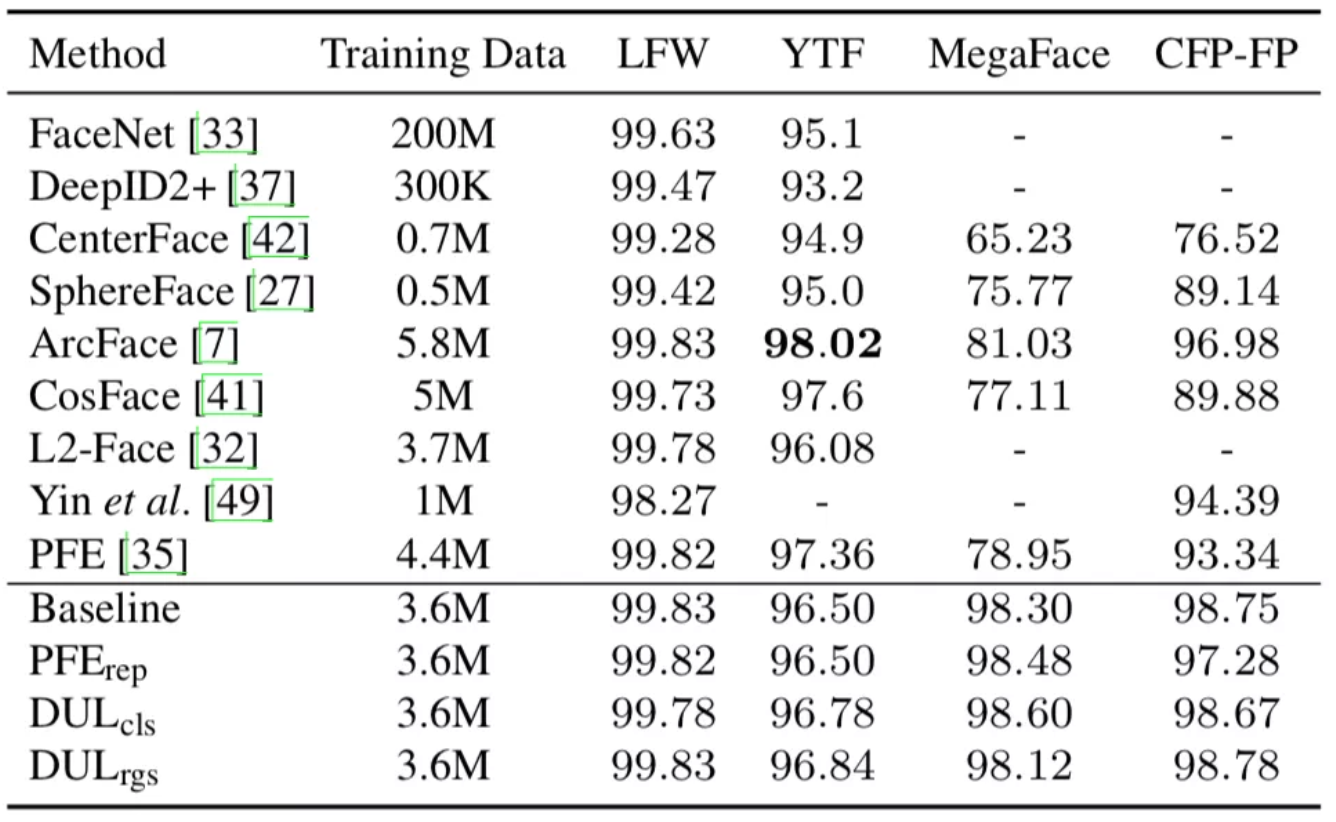
表2:在LFW、YTF、MegaFace (MF) 、CFP-FP数据集上,与当前最佳方法的对比结果
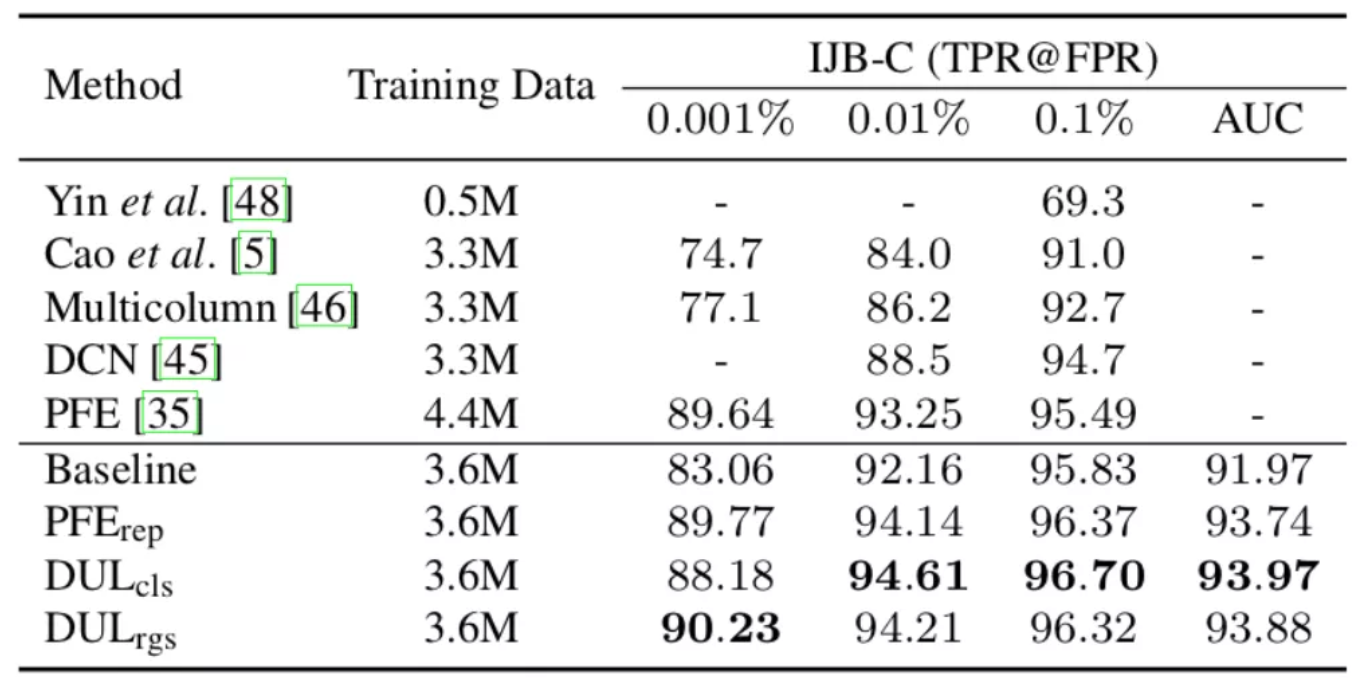
表3:在IJB-C数据集上,与当前最佳方法的对比结果,Back- bone: ResNet64
在LFW、YTF、MegaFace (MF) 、CFP-FP数据集上,DUL与当前最佳方法做了对比,结果如表2所示。注意,基线模型在LFW和CFP-FP数据集上的表现已经饱和,其中数据不确定学习的度量并不明显。但是,DUL\_cls/rgs依然在YTF和MegaFace9数据集上进一步提升了精度。表3给出了IJB-C数据集上不同方法的结果,PFE和DUL在基线模型上均取得了更优的性能。
模型鲁棒性
表5:在IJB-C数据集上,与当前最佳方法的对比结果,Back- bone: ResNet64
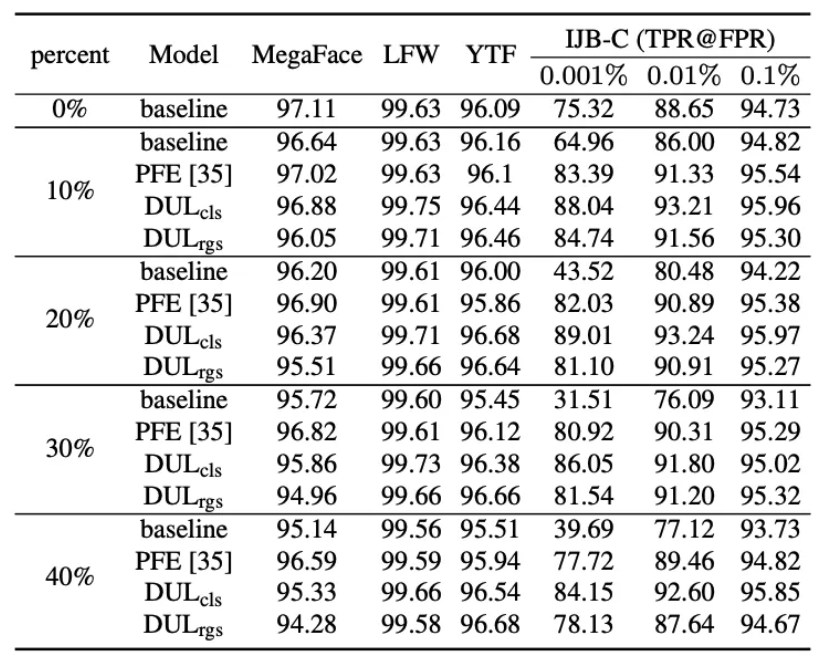
如表5所示,本文对于MS-Celeb-1M 人脸训练集进行手动的加噪实验。具体为针对不同比例的训练集样本施加高斯模糊,以创造 degradation 样本。实验结果表明,DUL 方法 和 PFE 均取得了相较基线模型更为鲁棒的结果。
结论
本文提出两个通用的学习方法,以进一步开发和优化人脸识别中的数据不确定性学习:DUL\_cls 和 DUL\_rgs。两种方法皆针对隐空间中的每个人脸图像给出一个高斯分布估计,并同时学习已估计均值的ID特征(均值)和不确定性(方差)。
相关实验表明,本文方法在大多数基准上性能优于确定性模型。另外,本文还通过定性分析和定量结果,从图像噪声的视角讨论了习得的不确定性如何影响模型训练。
参考文献
- Yichun Shi, Anil K Jain, and Nathan D Kalka. Probabilistic face embeddings. In Proceedings of the IEEE International Conference on Computer Vision, 2019.
- Alex Kendall and Yarin Gal. What uncertainties do we need in bayesian deep learning for computer vision? In Advances in neural information processing systems, pages 5574–5584, 2017.
- Jiankang Deng, Jia Guo, Niannan Xue, and Stefanos Zafeiriou. Arcface: Additive angular margin loss for deep face recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 4690– 4699, 2019.
- Weiyang Liu, Yandong Wen, Zhiding Yu, Ming Li, Bhiksha Raj, and Le Song. Sphereface: Deep hypersphere embedding for face recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 212–220, 2017.
- Florian Schroff, Dmitry Kalenichenko, and James Philbin. Facenet: A unified embedding for face recognition and clus- tering. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 815–823, 2015.
- Hao Wang, Yitong Wang, Zheng Zhou, Xing Ji, Dihong Gong, Jingchao Zhou, Zhifeng Li, and Wei Liu. Cosface: Large margin cosine loss for deep face recognition. In Pro- ceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 5265–5274, 2018.
- Yandong Wen, Kaipeng Zhang, Zhifeng Li, and Yu Qiao. A discriminative feature learning approach for deep face recog- nition. In European conference on computer vision, pages 499–515. Springer, 2016.
专栏文章推荐
- CVPR 2020 | 旷视研究院提出新方法,优化解决遮挡行人重识别问题
- CVPR 2019 | 新型损失函数:改善边界框模糊问题
- CVPR 2020 | 旷视研究院16篇(含6篇Oral)收录论文亮点集锦
欢迎关注旷视研究院极术社区专栏,定期更新最新旷视研究院成果
加入旷视:career@megvii.com