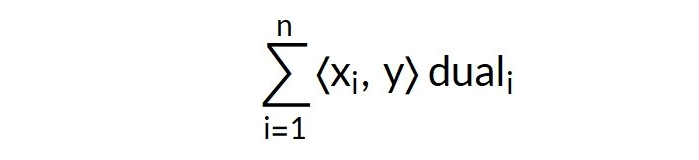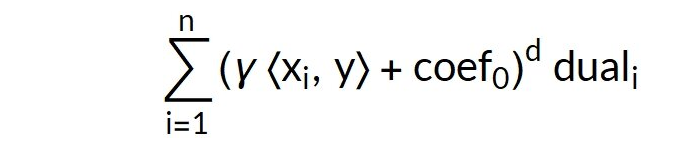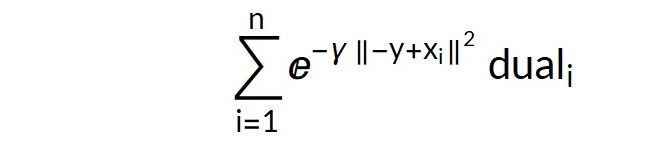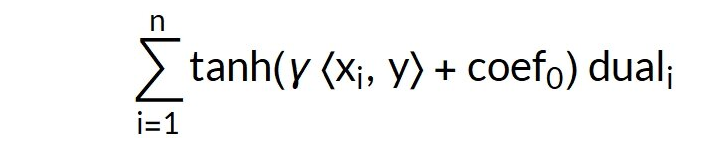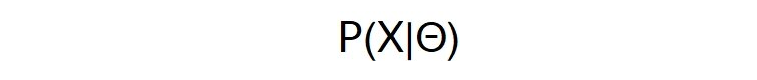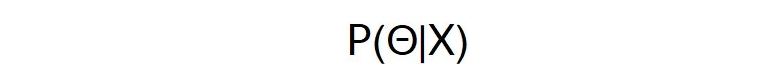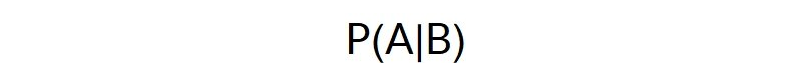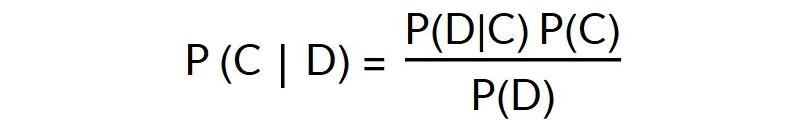总览
通常,当开发人员谈论机器学习(ML)时,他们指的是神经网络(NNs)。神经网络的最大优点是您不需要成为领域专家,就可以快速获得有效的解决方案。神经网络的缺点是它们通常需要大量的内存和周期,并且很难解释它们是如何得出结论的。
机器学习领域包括神经网络以外的技术。那些其他技术可能以其他名称使用,例如统计机器学习。在本指南中,我们使用经典机器学习的名称来指代CMSIS-DSP开源库中其他技术的使用。
CMSIS-DSP库是Arm针对各种Arm Cortex-M处理器(例如Cortex-M4,Cortex-M7,Cortex-M33,Cortex-M35和Cortex-M55处理器)优化的丰富的DSP函数的集合。Arm Developer网站包含有关这些处理器的更多信息和支持资源。
CMSIS-DSP在行业中得到了广泛使用,并能够通过各种第三方工具优化C代码生成。Arm最近为经典ML的CMSIS-DSP库添加了新功能,包括支持向量机(SVM),朴素的高斯贝叶斯分类器和聚类距离。
本指南说明了如何在Python中训练SVM和贝叶斯分类器,如何转储参数以及如何在CMSIS-DSP中使用转储的参数。它还说明了距离函数如何用于构建聚类算法。
这些分类器可用于异常检测,声音分类和图像识别。它们将需要使用智能功能,例如信号处理链的输出,对域的理解,并且将使用比神经网络更少的类。
CMSIS-DSP中提供的经典ML功能仅在float32中可用。
开始前的准备
要完成本指南,您应该知道如何构建CMSIS-DSP。
您还需要安装以下资源:
CMSIS-DSP的副本 [https://github.com/ARM-softwa...]
带有scikit-learn软件包的 Python 3 。[https://scikit-learn.org/stable/]
如果要显示图片,还应该在Python中安装matplotlib。
注意:Arm Keil MDK或Arm Development Studio项目默认不包括新的经典ML函数。要使用这些功能,您将必须重建库并将其包括在内。
新功能包含在以下CMSIS-DSP文件夹中:
- SVM功能
- 贝叶斯函数
- 距离功能
- 支持功能
- 统计功能
什么是支持向量机?
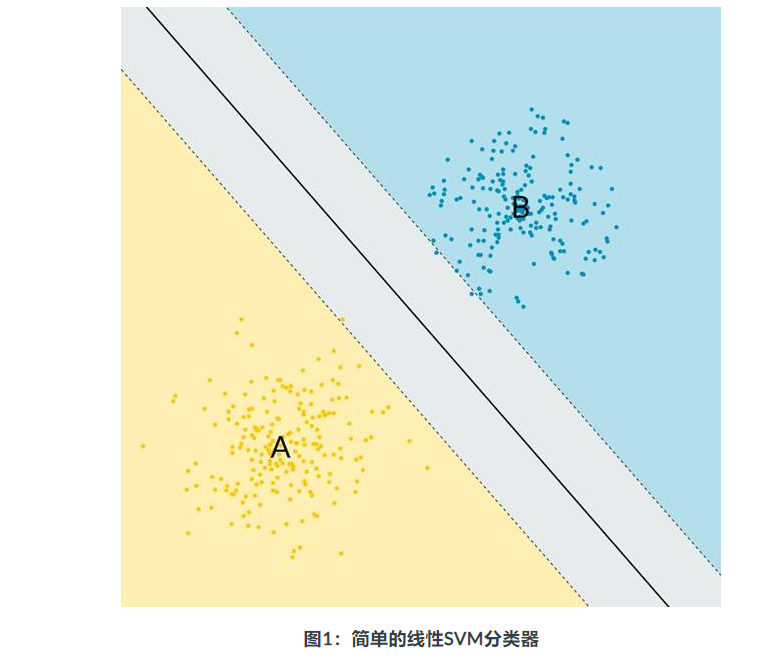
支持向量机(SVM)的概念很简单:使用一条线将两个点集群分开,如下图所示。黑线将群集B与群集A分开:
SVM分类器是二进制分类器。只有两种class。实际上,这些点通常不是平面中的点。相反,这些点是高维空间中的特征向量,因此该线是一个超平面。
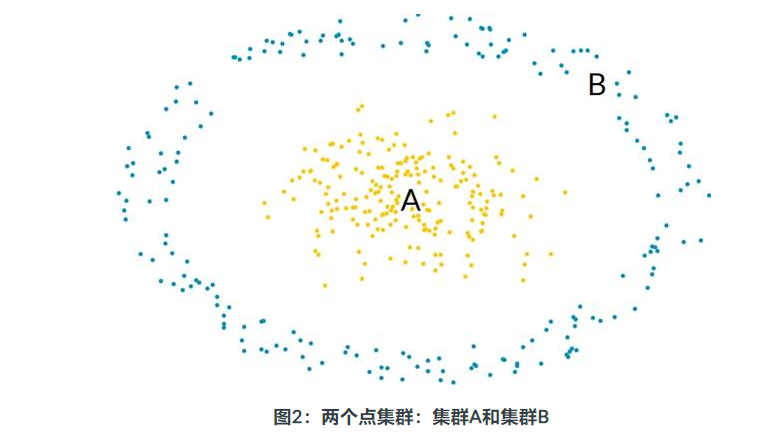
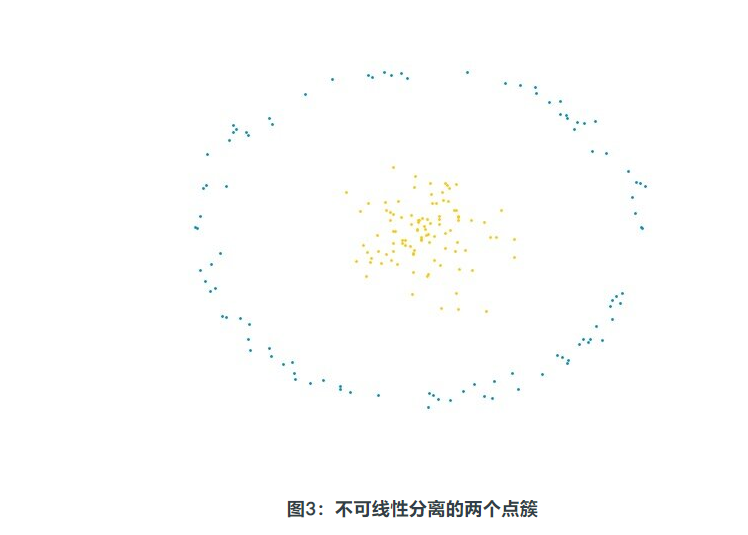
同样,没有理由将两个点的簇与一个超平面分开,如下图所示:
群集A和B不能被平面分开。为了解决此问题,SVM算法引入了非线性变换。
在CMSIS-DSP中,支持四种转换,因此可以使用四种SVM分类器。这些分类器使用由训练过程生成的向量,支持向量和系数,称为对偶系数。
线性分类器
线性预测使用以下公式:
在训练期间生成支持向量xi和对偶系数。要分类的向量是y。<x,y>是向量x和y之间的标量积。
该表达式的符号用于将向量y分类为A类或B类。
多项式分类器
多项式分类器使用以下公式:
该公式比线性分类器的公式复杂。训练期间会生成几个新参数:
- Gamma
- coef0
- 多项式的度
径向基函数
径向基函数分类器使用以下公式:
Sigmoid
Sigmoid分类器使用以下公式:
该公式类似于多项式公式,但是使用tanh代替计算表达式的幂。
由于多项式SVM是需要最多参数的SVM分类器,因此在本指南中以多项式SVM为例。您将学习如何在Python中训练多项式分类器,以及如何转储参数以在CMSIS-DSP中使用训练后的分类器。
使用scikit-learn训练SVM分类器
在本指南的这一部分中,我们重点介绍如何使用scikit-learn训练SVM分类器以及如何转储参数以用于CMSIS-DSP。本活动的数据生成和可视化部分超出了本指南的范围。
可以在CMSIS-DSP库中找到以下代码:
CMSIS / DSP / Examples / ARM / arm_svm_example / train.py
您可以运行此示例以重现本指南的结果,以便可以生成数据,训练分类器并显示一些图片。
让我们看一下该脚本中与参数的训练和转储相对应的部分。
SVM分类器的训练依赖于scikit-learn库。因此,我们必须从sklearn模块导入svm。
训练需要一些数据。为数据生成部分导入了random,numpy和math Python模块。图形可视化需要更多模块。在train.py文件中对此进行了描述。
以下Python代码加载了所需的模块:
from sklearn import svm
import random
import numpy as np
import math数据由两个100点的群集组成。第一个簇是一个以原点为中心的球。第二簇具有围绕原点和前一个球的环形空间。
此图显示了这些点簇的样子:
点的簇是使用以下Python代码生成的。此代码生成随机点,并准备用于训练分类器的数据。数据是点数组和相应类的数组:X_train和Y_train
黄色点对应于等级0,蓝色点对应于等级1。
NBVECS = 100
VECDIM = 2
ballRadius = 0.5
x = ballRadius * np.random.randn(NBVECS, 2)
angle = 2.0 * math.pi * np.random.randn(1, NBVECS)
radius = 3.0 + 0.1 * np.random.randn(1, NBVECS)
xa = np.zeros((NBVECS,2))
xa[:, 0] = radius * np.cos(angle)
xa[:, 1] = radius * np.sin(angle)
X_train = np.concatenate((x, xa))
Y_train = np.concatenate((np.zeros(NBVECS), np.ones(NBVECS)))以下两行使用我们刚刚定义的数据创建和训练多项式SVM分类器:
clf = svm.SVC(kernel='poly',gamma ='auto',coef0 = 1.1)
clf.fit(X_train,Y_train)您可以在下图中看到训练的结果:
实线表示两个类别之间的分离,如SVM分类器所学。
图像上较大的红点是用于检查分类器的两个测试点。
图像中心附近的红点位于类别0内。图像边缘附近的红点对应于类别1。
以下代码在中心群集内创建第一个点,即类0,并应用分类器。预测1的结果应为0:
test1 = np.array([0.4,0.1])
test1 = test1.reshape(1,-1)
predicted1 = clf.predict(test1)
print(predicted1)现在,我们想将此训练有素的分类器与CMSIS-DSP一起使用。为此,必须转储分类器的参数。
CMSIS-DSP多项式SVM使用以下代码中所示的实例结构。CMSIS-DSP需要此结构的参数,并且必须从Python脚本中转储该参数:
typedef struct
{
uint32_t nbOfSupportVectors; / ** <支持向量的数量* /
uint32_t vectorDimension; / ** <向量空间的尺寸* /
float32_t截距;/ ** <拦截* /
const float32_t * dualCoefficients; / ** <对偶系数* /
const float32_t * supportVectors; / ** <支持向量* /
const int32_t * classs; / ** <两个SVM类* /
int32_t度;/ ** <多项式* /
float32_t coef0; / ** <多项式常数* /
float32_t gamma; / ** <伽玛系数* /
} arm_svm_polynomial_instance_f32;其他SVM分类器,例如线性,S型和rbf,也以类似的方式使用,但与多项式相比需要更少的参数。这意味着,一旦您知道如何为多项式SVM转储参数,就可以对其他类型的SVM分类器执行相同的操作。
以下Python脚本从训练有素的SVM分类器访问参数,并打印要在CMSIS-DSP中使用的值:
supportShape = clf.support_vectors_.shape
nbSupportVectors = supportShape [0]
vectorDimensions = supportShape [1]
print(“ nbSupportVectors =%d”%nbSupportVectors)
print(“ vectorDimensions =%d”%vectorDimensions)
print(“ degree =%d”% clf.degree)
print(“ coef0 =%f”%clf.coef0)
print(“ gamma =%f”%clf._gamma)
print(“ intercept =%f”%clf.intercept_)支持向量和对偶系数是CMSIS-DSP中的数组。可以使用以下代码打印它们:
dualCoefs = clf.dual_coef_
dualCoefs = dualCoefs.reshape(nbSupportVectors)
supportVectors = clf.support_vectors_
supportVectors = supportVectors.reshape(nbSupportVectors * VECDIM)
print("Dual Coefs")
print(dualCoefs)
print("Support Vectors")
print(supportVectors)使用CMSIS-DSP实现您的SVM
一旦从Python代码中转储了SVM分类器的参数,就可以在CMSIS-DSP的C代码中使用它们。
您可以在
CMSIS / DSP / Examples / ARM / arm_svm_example / arm_svm_example_f32.c中找到完整的代码
本示例通过使用相同的测试点来重现Python预测。以下代码声明了SVM分类器使用的实例变量和一些长度。
这个实例变量将包含从Python转储的所有参数。
其中一些参数是数组,因此我们必须指定一些大小,例如支持向量的数量及其尺寸。
以下代码定义了实例变量和一些大小,这在以后创建数组时将很有用。
arm_svm_polynomial_instance_f32 params;
#define NB_SUPPORT_VECTORS 11
#define VECTOR_DIMENSION 2以下代码定义了2个数组。对偶系数和支持向量的数组填充有来自Python的值。还定义了类0和1以简化与Python的比较:
const float32_t dualCoefficients [NB_SUPPORT_VECTORS] = {
-0.01628988f,-0.0971605f,
-0.02707579f,0.0249406f,
0.00223095f,0.04117345f,
0.0262687f,0.00800358f,
0.00581823f,0.02346904f,
0.00862162f}}; / ** <对偶系数* /
const float32_t supportVectors [NB_SUPPORT_VECTORS * VECTOR_DIMENSION] = {
1.2510991f,0.47782799f,
-0.32711859f,-1.49880648f,
-0.08905047f,1.31907242f,
1.14059333f,2.63443767f,
-2.625615024f,1.02 f,
-1.2361353f,-2.53145187f,
2.28308122f,-1.58185875f,
2.73955981f,0.35759327f,
0.56662986f,2.79702016f,
-2.51380816f,1.29295364f,
-0.56658669f,-2.81944734f};/ ** <支持向量* /
const int32_t classes [2] = {0,1};以下代码使用来自Python的所有参数初始化实例变量,例如,长度,上述数组以及拦截,度,coef0和gamma参数:
arm_svm_polynomial_init_f32(¶ms,
NB_SUPPORT_VECTORS,
VECTOR_DIMENSION,
-1.661719f,/ *截距* /
dualCoefficients,
supportVectors,
类,
3,/ *度* /
1.100000f,/ * Coef0 * /
0.500000f / *伽玛* /
);最后,为了进行测试,使用多项式SVM预测器定义并分类了输入向量。
以下代码定义输入向量并应用分类器:
in [0] = 0.4f;
in [1] = 0.1f;
arm_svm_polynomial_predict_f32(¶ms,
in,
&result);输入向量是一个点。该点被定义为位于中心类中,该类对应于类0。该点的坐标与Python代码中用于测试分类器的点相同。因此,以上代码的结果应为类0。
SVM分类器是二进制分类器。如果要使用更多的类,则需要为每个不同的类对创建分类器,并对结果进行多数表决以选择最终的类。
例如,在以下来自scikit-learn的示例中,SVM用于识别数字。十位数有45对。这意味着有45个SVM分类器。Scikit-learn使用一对一策略自动创建它们:将每个分类与其他每个分类进行比较。
在这种情况下,参数的提取更加复杂,因为scikit-learn返回包含所有45个分类器参数的矩阵。在CMSIS-DSP中,您需要45个实例变量,然后从矩阵中提取值以初始化所有这些实例变量。
什么是贝叶斯估计器?
如果估计器使用贝叶斯定理来预测某些观测数据的最可能类别,则它就是贝叶斯估计器。
由于数据类别是未知参数,而不是随机变量,因此无法使用概率的标准概念来表示该类别的概率。
贝叶斯概率使用不同的概率概念,它量化了我们对断言真相的知识状态。
对于标准概率,假设未知参数theta的某个值,则某些随机变量X的条件概率无法反转。
您可以编写以下公式,因为X是随机变量:
但是您不能编写以下公式,因为theta不是随机变量,而是一个未知参数:
贝叶斯概率使您可以表达某些逻辑断言为真的概率。
这意味着假设B的条件概率A具有对称性,用以下公式表示:
A和B都是逻辑断言。因此,可以使用贝叶斯定理对先前的公式进行求逆,以得出假设A为B的概率。
如果A和B是观测数据D和数据C的类别,则贝叶斯定理可让您关联对数据和类别的了解。
如果您对数据如何依赖类有一些了解,贝叶斯定理可以让您为观察到的数据计算最可能的类。
假设某些观测数据的一类概率表示为P(C | D)。假设某类C的数据的概率表示为P(D | C)。
贝叶斯定理如下所示:
对于朴素的高斯贝叶斯分类器,数据D是样本的向量。我们假设样本是独立的,并且它们遵循高斯分布。
每个类别的高斯参数将在训练Python分类器时计算。对于每个高斯,均值和标准差都会计算出来。
同样,如果有关类别的某些信息可用,而某些类别或多或少的可能性很大,则此知识将编码在先验概率P(C)中。
Python代码还会返回一个值epsilon,这对于数值精度是必需的。
使用scikit-learn训练您的贝叶斯估计器
在本指南的这一部分中,我们描述了如何使用scikit-learn训练贝叶斯分类器以及如何转储参数以用于CMSIS-DSP。本活动的数据生成和可视化部分超出了本指南的范围。
文件CMSIS / DSP / Examples / ARM / arm_bayes_example / train.py包含此示例的所有代码。
您可以运行此文件以重现本指南的结果,并生成数据并训练分类器。
在示例中,存在三个聚类:A,B和C。每个聚类中的样本都是使用高斯分布生成的。
下图显示了三个点簇:
贝叶斯分类器的训练依赖于scikit-learn库。因此,我们必须从sklearn.naive_bayes模块导入GaussianNB。
培训需要一些数据。随机,numpy和数学Python模块已导入,用于本练习的数据生成部分。
以下Python代码加载了所需的模块:
from sklearn.naive_bayes import GaussianNB
import random
import numpy as np
import math以下代码生成三个点集群:
# 3 cluster of points are generated
ballRadius = 1.0
x1 = [1.5, 1] + ballRadius * np.random.randn(NBVECS,VECDIM)
x2 = [-1.5, 1] + ballRadius * np.random.randn(NBVECS,VECDIM)
x3 = [0, -3] + ballRadius * np.random.randn(NBVECS,VECDIM)所有要点及其班级都串联起来进行培训。
群集A为0类,群集B为1类,群集C为2类。
以下代码通过串联三个集群来创建输入数组。此代码还通过连接类编号来创建输出数组:
# All points are concatenated
X_train=np.concatenate((x1,x2,x3))
# The classes are 0,1 and 2.
Y_train=np.concatenate((np.zeros(NBVECS),np.ones(NBVECS),2*np.ones(NBVECS)))以下代码在刚创建的输入数组上训练高斯朴素贝叶斯分类器:
gnb = GaussianNB()
gnb.fit(X_train, Y_train)我们可以通过对每个聚类中的一个点进行分类来检查结果。
下面的代码检查是否将群集A中的点识别为在群集A中。群集A的类号为0。这意味着执行此代码时y_pred应该为0:
y_pred = gnb.predict([[1.5,1.0]])
print(y_pred)现在,我们想将此训练有素的分类器与CMSIS-DSP一起使用。为此,必须转储分类器的参数。
CMSIS-DSP贝叶斯分类器使用以下代码中所示的实例结构。CMSIS-DSP需要此结构的参数,并且必须从Python脚本中转储该参数:
typedef struct
{
uint32_t vectorDimension; / ** <向量空间的维数* /
uint32_t numberOfClasses; / ** <不同类别的数量* /
const float32_t * theta; / ** <高斯平均值* /
const float32_t * sigma; / ** <高斯变量* /
const float32_t * classPriors; / ** <class先验概率* /
float32_t epsilon; / ** <方差的加法* /
} arm_gaussian_naive_bayes_instance_f32;可以使用以下Python代码转储所需的参数:
print(“ Parameters”)
#高斯平均值
print(“ Theta =”,list(np.reshape(gnb.theta_,np.size(gnb.theta_))))
#高斯方差
print(“ Sigma =”,list(np .reshape(gnb.sigma_,np.size(gnb.sigma_))))
#类优先级
print(“ Prior =”,list(np.reshape(gnb.class_prior_,np.size(gnb.class_prior_))))
print (“ Epsilon =”,gnb.epsilon_)使用CMSIS-DSP实现您的贝叶斯估计器
一旦从Python代码中转储了贝叶斯分类器的参数,就可以在CMSIS-DSP的C代码中使用它们。
您可以在CMSIS / DSP / Examples / ARM / arm_bayes_example / arm_bayes_example_f32.c中找到完整的代码
本示例通过使用相同的测试点来重现Python预测。
以下代码声明贝叶斯分类器使用的实例变量和一些长度。
此实例变量包含所有已从Python转储的参数。
其中一些参数是数组。这意味着我们必须使用类数和向量维数指定它们的大小:
arm_gaussian_naive_bayes_instance_f32 S;
#define NB_OF_CLASSES 3
#define VECTOR_DIMENSION 2需要三个参数数组:
- 高斯平均值(theta)
- 高斯方差(sigma)
- class先验概率
以下代码定义了数组的内容。这些值是从Python转储的:
const float32_t theta [NB_OF_CLASSES * VECTOR_DIMENSION] = {
1.4539529436590528f,0.8722776016801852f,
-1.5267934452462473f,0.903204577814203f,
-0.15338006360932258f,-2.9997913665803964f
}; / ** <高斯平均值* /
const float32_t sigma [NB_OF_CLASSES * VECTOR_DIMENSION] = {
1.0063470889514925f,0.9038018246524426f,
1.0224479953244736f,0.7768764290432544f,
1.1217662403241206f,1.2303890106020325f
}; / ** <高斯变量* /
const float32_t classPriors [NB_OF_CLASSES] = {
0.3333333333333333f,0.3333333333333333f,0.3333333333333333f
}; / ** <class先验概率* /以下代码使用来自Python的数组,某些大小和epsilon值填充实例变量字段。
S.vectorDimension = VECTOR_DIMENSION;
S.numberOfClasses = NB_OF_CLASSES;
S.theta = theta;
S.sigma = sigma;
S.classPriors = classPriors;
S.epsilon = 4.328939296523643e-09;一旦数据结构被初始化,就可以使用分类器。分类器估计每个类别的概率。但是,此分类器不是一个很好的估计器。这意味着不应使用概率值,除非要找到给出样本最可能类别的最大概率。
以下代码在类A对应的类A内的样本点上测试分类器。
为了找到类别,代码将寻找最大概率,从而给出最可能的类别。
in [0] = 1.5f;
in [1] = 1.0f;
arm_gaussian_naive_bayes_predict_f32(&S,in,result);
arm_max_f32(result,
NB_OF_CLASSES,
&maxProba,
&index);
printf(“ Class =%d \ n”,index);什么是聚类?
聚类是将一组点划分为相似点的不同簇的尝试。为了做到这一点,我们需要一种方法来测量这些点的接近程度或相似程度。为此,许多聚类算法都依赖于距离函数。
下图显示了使用三个不同距离函数的聚类算法的结果,并试图从均匀分布的点中识别出五个不同的聚类。
CMSIS-DSP不提供任何聚类算法。相反,CMSIS-DSP提供了距离函数,可用于构建聚类算法。
使用距离构建聚类分类器需要一种快速找到一个点与其他点之间的距离的方法。对此的策略超出了CMSIS-DSP库的范围。
使用CMSIS-DSP距离功能
CMSIS-DSP提供了通常在聚类算法中使用的大多数距离功能。它包括浮点数和布尔值的距离函数。
CMSIS-DSP中的所有距离功能都具有类似的API。让我们以曼哈顿距离(也称为城市街区距离)为例。
以下代码描述了街区距离的API:
float32_t arm_cityblock_distance_f32(const float32_t * pA,
const float32_t * pB,
uint32_t blockSize);此函数计算块大小的两个向量pA和pB之间的距离。
文件夹CMSIS / DSP / DistanceFunctions也包含从数学观点来看并不是真正距离的函数。例如,余弦距离是相似度的量度。
其他新的CMSIS-DSP功能
如果您要构建更复杂的Classical-ML算法,本指南本节中列出的功能将很有用。
CMSIS-DSP引入了两个新功能,这些功能在计算点或标量的加权和时很有用。
arm_ barycenter_f32
是一种实用程序函数,用于计算某些加权点的重心。
arm_weighted_sum_f32
使用标量并计算这些标量的加权和。
以下代码描述了这些功能的API:
void arm_barycenter_f32(const float32_t * in,
const float32_t * weights,
float32_t * out,
uint32_t nbVectors,
uint32_t vecDim);
float32_t arm_weighted_sum_f32(const float32_t * in,
const float32_t * weigths,
uint32_t blockSize);CMSIS-DSP引入了两个与熵有关的新功能。
arm_entropy_f32
计算概率分布pSrcA的熵。
arm_kullback_leibler_f32
计算两个概率分布之间的Kullback Leibler散度。
以下代码描述了这些功能的API:
float32_t arm_entropy_f32(const float32_t * pSrcA,
uint32_t blockSize);
float32_t arm_kullback_leibler_f32(const float32_t * pSrcA,
const float32_t * pSrcB,
uint32_t blockSize);当以高斯概率进行运算时,舍入问题可能会成为问题。这是因为值的动态可能很大。相反,您可以使用值的自然对数log。
arm_logsumexp_f32
计算它们的日志表示的概率之和。该总和的计算考虑了精度问题。
arm_logsumexp_dot_prod_f32
当值由它们的日志表示时,计算点积。
使用表表示的条件概率时,通常需要计算这些矩阵的行和列之间的点积。如果概率由它们的日志值表示,则需要使用类似arm_logsumexp_dot_prod_f32的函数。
以下代码描述了这些功能的API:
float32_t arm_logsumexp_dot_prod_f32(const float32_t * pSrcA,
const float32_t * pSrcB,
uint32_t blockSize,
float32_t * pTmpBuffer);
float32_t arm_logsumexp_f32(const float32_t * in,uint32_t blockSize);