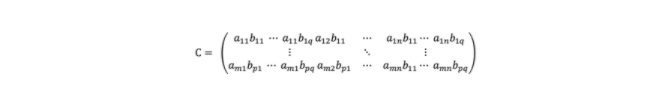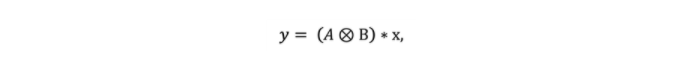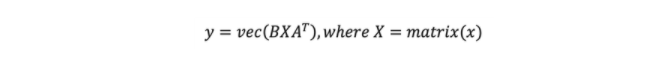TinyML应用需求新的网络架构

Urmish Thakker
2020年2月13日

为什么是TinyML？

研究人员研究神经网络压缩已经有很长一段时间了。然而，对始终在线计算需求导致了最近的一种趋势，即在更小的物联网设备上执行这些应用程序。这些设备的总系统内存可以是1MB，也可以低至几千字节。然而，传统上用于运行这些应用程序的神经网络可能非常庞大，在TinyML设备上安装它们需要极大的压缩。例如，要在具有1MB缓存的设备上高效运行大小为25MB的长期短期内存(LSTM)层，至少需要25倍的压缩。在2KB的缓存上运行中基于递归神经网络(RNN)的关键字识别应用程序需要25-38倍的压缩。

我们为什么要重新考虑网络架构？

传统的技术，剪枝和低阶矩阵分解(LMF)，以显著的精度损失为代价来实现如此高的压缩比。这是因为如此高的压缩率导致压缩网络中的矩阵具有较差的特性(失秩、病态)。因此，我们需要重新考虑设计这些架构的方式，以实现这些压缩因子。我们ARM一直在研究一种基于Kronecker产品的这样的结构。这项工作是对Google和Microsoft在该领域的先前工作的补充。初步结果令人振奋-我们能够使用各种Kronecker产品将物联网工作负载压缩为原来的1/16-1/38，将大型语言模型压缩为原来的1/25。我们的技术远远超过了传统压缩技术和以前最先进的技术所达到的精度。

概述

在这篇文章中，我们介绍了为资源受限的设备开发高效架构的工作。我们首先介绍了Kronecker产品，并讨论了将Kronecker乘积压缩应用于物联网领域基于序列的神经网络的最佳方法。接下来，我们来谈谈如何使用Kronecker产品来压缩较大的模型。这需要对Kronecker产品架构进行一些微调。我们把这种微调和由此产生的技术称为掺杂Kronecker产物。最后，我们讨论了训练掺杂Kronecker积的最佳学习方法。这包括通过使用称为共矩阵行丢失正则化的随机正则化方案来克服我们所称的共矩阵自适应。

Kronecker Products (KP)

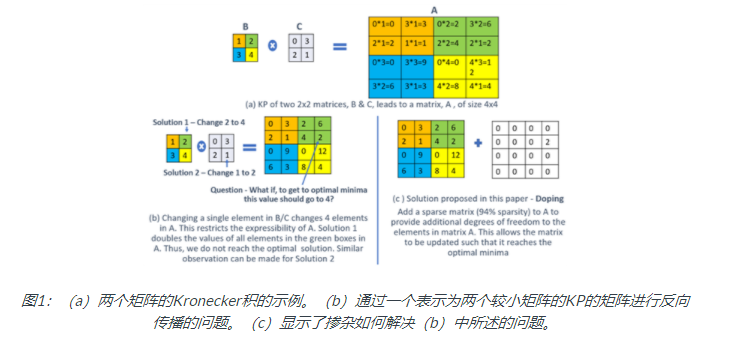
Kronecker积，用⊗表示，是对任意大小的两个矩阵进行的运算，其结果是一个更大的矩阵。如果A是m×n矩阵，B是p×q矩阵，则A和B的Kronecker积C由下式给出：

其中C是mp×nq块矩阵。

我们称A和B为C的Kronecker因子(Kfs)，C可以有多个这样的Kronecker因子，即C可以表示为A1⊗A2⊗…。⊗An.。

现在我们了解了Kronecker积是什么样子，让我们深入研究当一个矩阵被表示为多个较小KF的Kp时，推理是如何工作的。利用线性代数中的技巧，我们可以避免在推理过程中重构较大的矩阵，这就节省了计算量，也就是说。如果，

y为(mp X 1)向量，x是(nq x 1)输入向量，然后

这里，Matrix()函数是转置和重塑操作，vec()函数是转置和矢量化函数。当KF数大于3时，该公式递归应用。

使用Kronecker Products压缩网络的最佳实践

我们的第一项工作探索了以下问题。

我们应该把一个矩阵分解成多少个Kronecker因子？
使用这种分解技术对推理运行时有什么影响？
使用KP压缩后获得的压缩系数是多少？
与传统压缩技术相比，这些压缩网络的准确性如何？

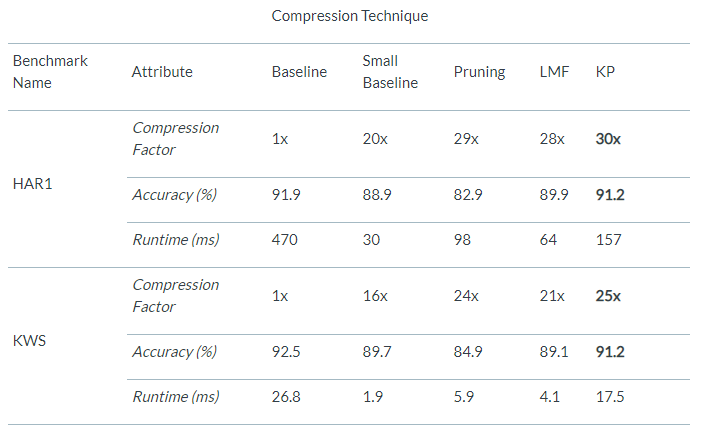
我们的研究表明，这样的矩阵的数量应该限制在两个。这是因为较多的KF会导致训练期间的梯度问题消失，以及与较慢的推理运行时间相关的问题。此外，文献[1]还给出了在最大化压缩后矩阵秩的同时进行最大压缩的算法。我们在基于物联网的时序网络上的结果是令人振奋的。KP可以将这些网络压缩16-38倍，同时获得比剪枝网络高9.6%的准确率和比LMF压缩网络高4.5%的准确率。我们在跨越3个物联网应用的5个基准测试中对该网络进行了评估。此外，与基准网络相比，KP压缩网络的运行时间提高了1.27-1.73倍。下表列出了其中一些结果。如果您发现这些结果令人兴奋，我们鼓励您阅读[1]来更深入地研究这种压缩技术。

将KP压缩扩展到更大的网络

我们尝试将KP从[5]扩展到大型语言模型(LM)。然而，这导致了近35%的精确度损失。这一损失是以338倍的压缩来实现的。传统的压缩技术，如剪枝和LMF，可以在网络中引入更多的参数以获得更好的精度，即降低压缩因子以获得更好的精度。修剪通过降低网络的稀疏性来实现这一点，而LMF通过提高矩阵的秩来实现这一点。在Kronecker的世界里，没有明显的相似之处。在[1]中，我们展示了一种这样的技术，混合KP。然而，对于LM基准测试，该技术在压缩约5倍的情况下实现了等精度，降低了KP的压缩能力。我们决定解决的下一个迫在眉睫的问题是探索一种在不牺牲KP压缩能力的情况下向KP压缩网络注入参数的方法。

Doped Kronecker Products (DKP)

为了理解为什么KP压缩不能扩展到更大的网络，我们关注的是在反向传播过程中梯度是如何流过KP压缩网络的。当我们关注梯度流时，我们意识到Kp空间中的参数需要额外的自由度(参见图1a，b)。受稳健PCA技术的启发，我们引入了稀疏覆盖矩阵来提供这些额外的自由度。我们最终结合了不同的压缩技术、稀疏性和KP。我们称这种压缩技术为掺杂Kronecker product(见图1c)。

训练DKP网络

训练DKP网络并非易事。在训练这些网络时，我们遇到了所谓的共矩阵自适应。这两个矩阵（KP压缩矩阵和稀疏矩阵）相互适应。这是在训练的初始阶段发生的，此时覆盖矩阵很密集，并且修剪尚未开始。这会导致容量损失，也就是说，其他参数不会导致精度提高。为了克服这个问题，我们在这些网络的可用性中引入了随机性。这种随机性是受辍学和随机深度概念的启发。为简便起见，我们不讨论这些学习方法的技术细节，而是遵照已发表的论文[2]。