MUX变身大法

老李今天给大家推一篇基础内容，帮大家复习一下数字电路里利用2选1的MUX如何来搭其他的门电路，这也是企业笔试的时候比较入门的考题，建议大家收藏这一篇，在笔试之前复习一遍，遇到此类问题就可以迅速秒过。

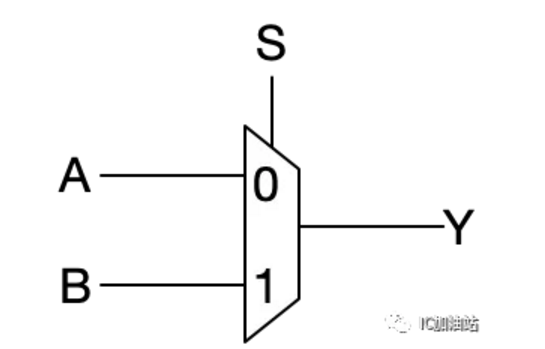
开始变换之前，我们先看一下2选1的MUX是什么。如下图所示

S为MUX的选择端，如果S为0，则选择A，MUX输出的Y=A，如果S为1，则选择B，MUX输出Y=B。在Verilog语言中，MUX的实现可以利用？：运算符，非常直观。在下面的示例中，我们用大写S, A, B分别表示MUX的三个输入pin，下面变换的实例的门输入信号都用小写字母来区分。

assign Y = S ? B : A;

01 MUX变反相器--难度0⭐️

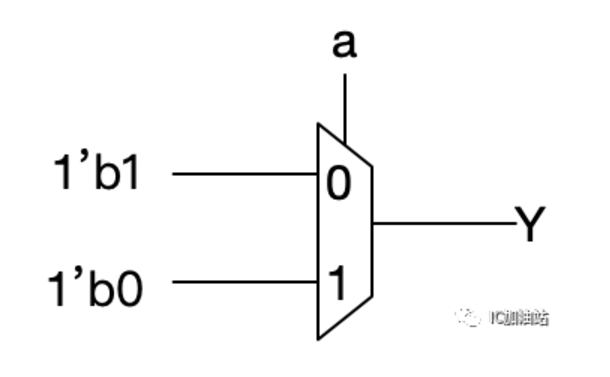
反相器Inverter只有一个输入a，输入是0，输出为1；输入为1，输出则为0。思路是将MUX的S作为输入a，那么当S为0，Y需要为1，那我们就需要A恒定为1；当S为1，Y需要为0，则需要B恒定为0。所以变化方法为

02 MUX变AND，OR门--难度0.5⭐️

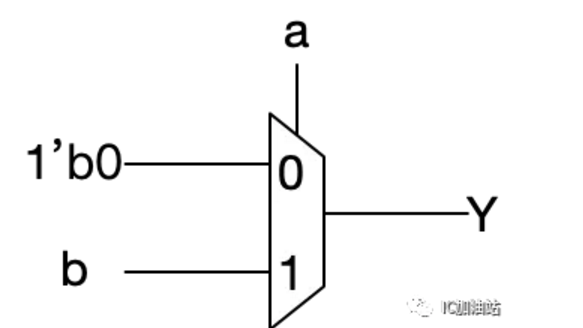
AND门是2输入的，设输入为a和b，那么当a和b同时为1时，输出才为1，其余只要有任意一个为0，输出则为0。这里变换的思路是，把a用来作为S，则Y的逻辑变为：当a为0时，无论b是什么，Y都为0; 当a为1时，Y取决于b的值，b为1，则Y为1，b为0，则Y为0。所以MUX的A输入连恒定的1'b0，MUX的B输入连b。

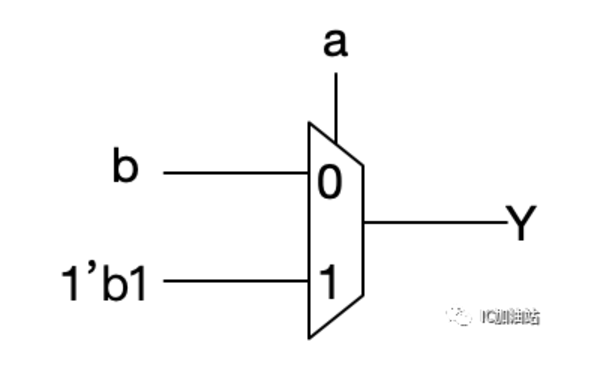
OR门则类似，当a和b同时为0时，输出才为0，其余只要有任意一个为1，输出则为1。还是利用a当S，a为0时，Y看b的值，a为1时，Y等于1。

03 MUX变NAND，NOR门--难度1⭐️

思路一：NAND门和NOR门无非就是AND门和OR门后面加个反相器，既然上面我们已经用MUX搭出了AND、OR还有反相器，那么可以组合起来。老李就不画了，大家心里清楚。

思路二：我们看NAND的真值表


a	b	Y
0	0	1
0	1	1
1	0	1
1	1	0

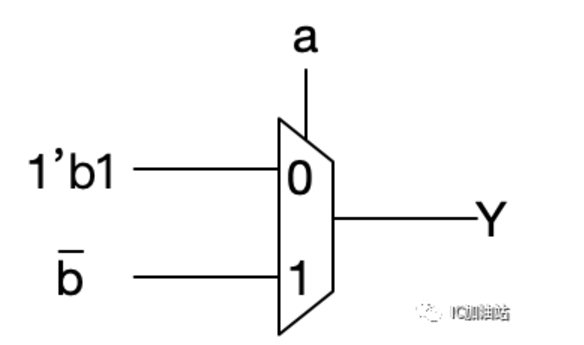
如果还是拿a当S，那么可以看出，当a=0时，Y恒定为1，当a=1时，Y为b的反。那么可以得出

这种思路看似只用一个MUX，但是b的反如果没有给你的话，其实你还是得需要一个反相器。

对于NOR来说


a	b	Y
0	0	1
0	1	0
1	0	0
1	1	0

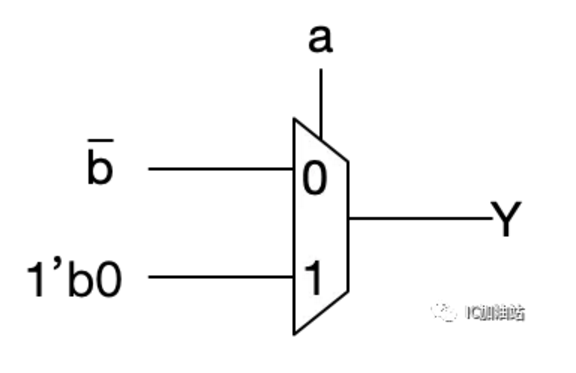
a接S，当a为1时，Y恒定为0，当a为0时，Y为b的反

04 MUX变XOR，XNOR门--难度1.5⭐️

XOR门是如果两个输入相反，则输出为1，如果输入相同，则输出为0。XOR的真值表为


a	b	Y
0	0	0
0	1	1
1	0	1
1	1	0

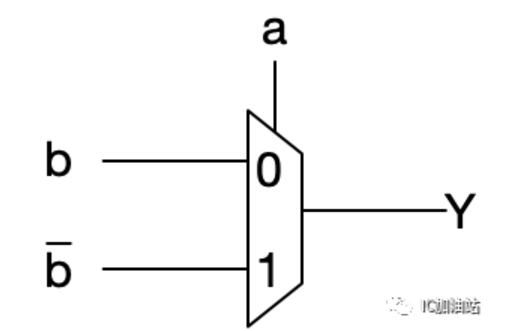
可以看出，a当S，则当a=0时，Y和b相同，但是当a=1时，Y为b的反

XNOR门是如果输入相同，则输出1，输入相反，则输出0。和上面刚好反过来


a	b	Y
0	0	1
0	1	0
1	0	0
1	1	1

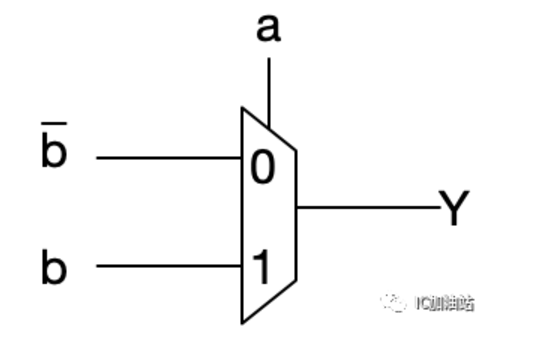
a当S，则当a=1时，Y和b相同，但是当a=0时，Y为b的反

05 MUX变3输入AND，3输入OR门--难度2.0⭐️

3输入的AND门，设输入为a,b,c，那么只有当a,b,c都为1的时候Y才为1，其余所有情况Y都为0。

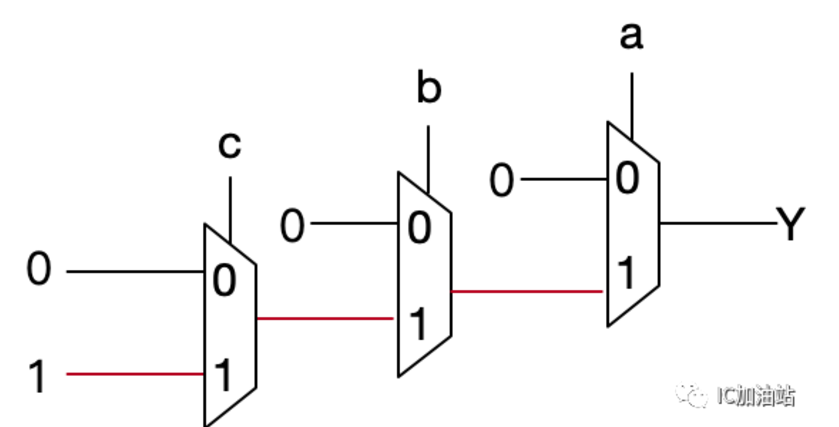
思路1：让a, b, c作为三个MUX的S端，三个MUX依次串起来，只有a,b,c都为1的选中的那一路为1，其余路全部为0。

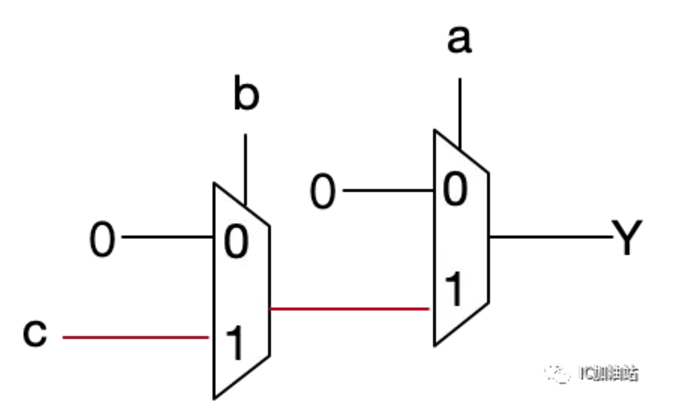
但是其实可以更简单一点，简化一个MUX，

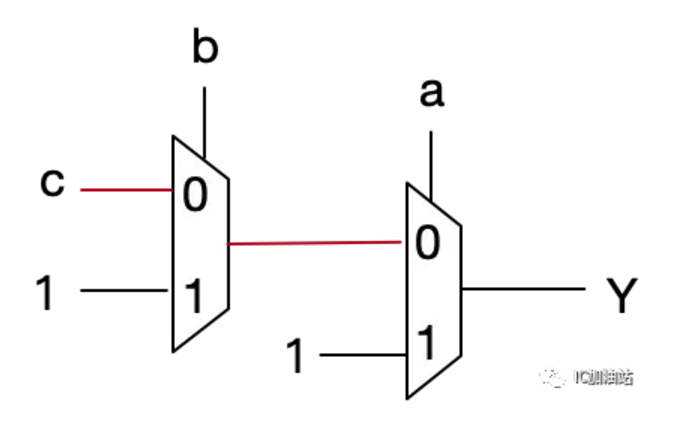
对于3输入OR门，则反过来，只有abc都为0的时候Y才为0，所以要在为0的那一条路径上下手

06 MUX变3输入NAND，3输入NOR门--难度2.5⭐️

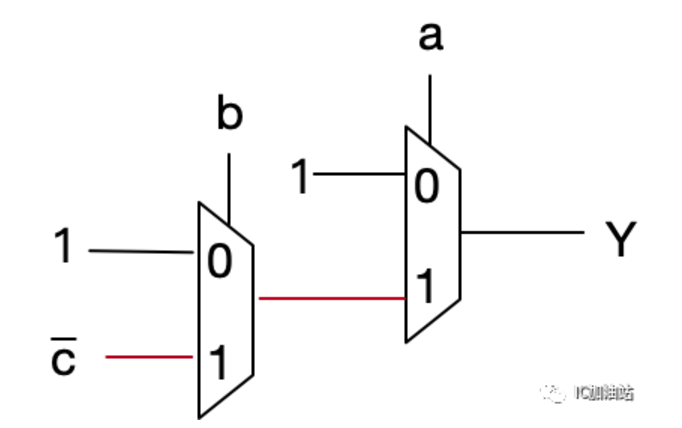
对于3输入NAND，和AND相反，当a,b,c都为1时，输出为0，其余所有情况输出都为1。依然利用a,b作为2个MUX的S端，可以类似得到

对于3输入NOR，则和OR相反，当a,b,c都为0时，输出为1，其余所有情况输出为0。

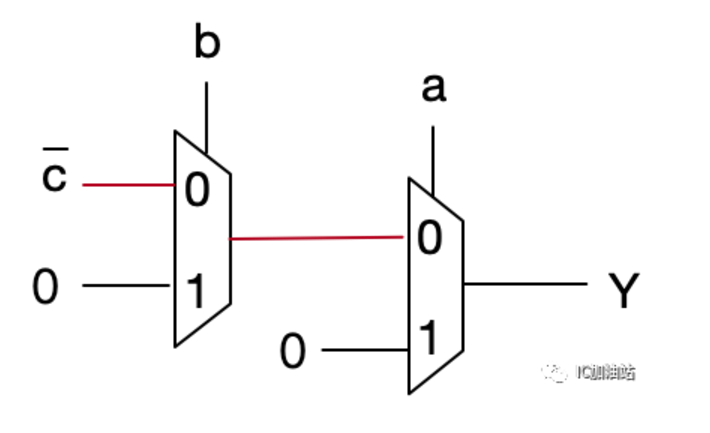
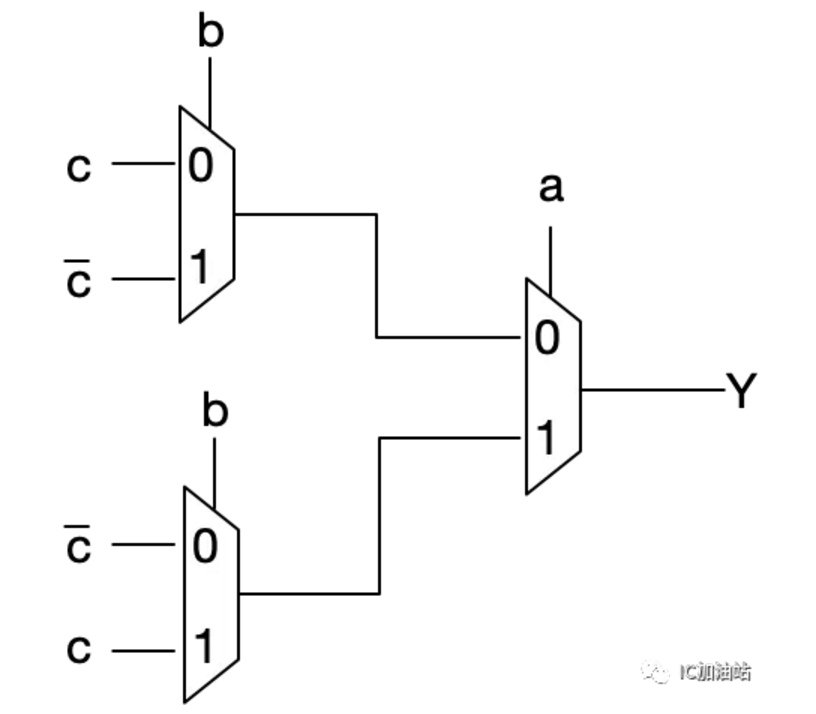
07 MUX变3输入XOR，3输入XNOR门--难度3⭐️

我们先来复习一下3输入XOR的逻辑，当a, b, c中有奇数个1的时候，结果为1，如果有0个或偶数个1，结果为0。真值表如下


a	b	c	Y
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

我们还是先将a作为一个MUX的S端，将真值表分为上下两半部分。再观察上下两半部分，再将b作为另外一个MUX的S端，观察剩下的，可以看出，利用b作为S端的MUX只有一个是不够的，需要两个。对于上半部分的来说，b=0时，Y和C一致（绿色），b=1时，Y和C相反（红色）。而下半部分刚好又和上面反过来，b=0时，Y和C相反（红色），b=1时，Y和C一致（绿色）。那么我们就可以得出

XNOR就当做练习大家自己画一下。

07 用2选1MUX搭半加器Half Adder--难度2.5⭐️

我们先来复习一下Half Adder是什么，半加器就是一个加法器电路，只有输入a, b，分别为1bit，而且不考虑进位Cin，结果为S和下一位进位Cout。真值表为


a	b	S	Cout
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

可以看出，S=a XOR b， Cout = a AND b。其实这个表达式建议大家记住。XOR有个符号⊕，老李觉得可以把它理解为加法器的加，这样就很好记：S=a⊕b，Cout = a & b。那利用MUX来搭XOR和AND门上面都讲过了，所以没有什么难度，这里就不重复画了。

08 用2选1MUX搭全加器Full Adder--难度3.5⭐️

全加器和半加器相比变为3输入，需要考虑输入进位Cin，真值表变为


a	b	Cin	S	Cout
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

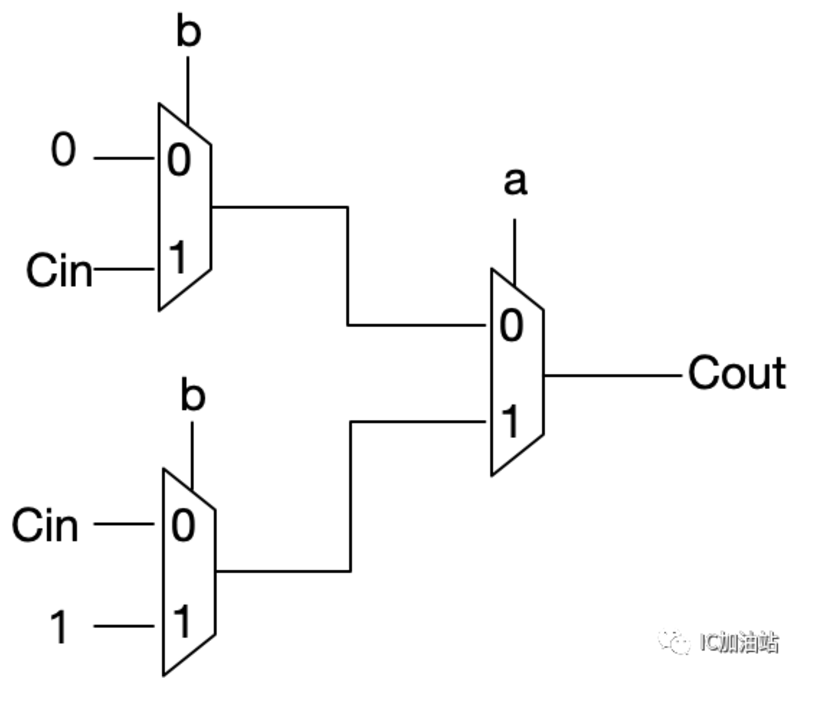
仔细观察可以看出，S=a⊕b⊕Cin。Cout = ab + aCin + bCin。老李还是建议大家把这两个表达式直接记住，不用现推。

那么和S的做法前面已经提过，即3输入的XOR门。

我们来看Cout，还是将a作为一个MUX的S端，将真值表分为上下两半部分，分别来看：上半部分a=0，当b=0时，Cout恒定为0，当b=1时，Cout=Cin；下半部分a=1，当b=0时，Cout=Cin，b=1时，Cout恒定为1。所以搭出来的电路为

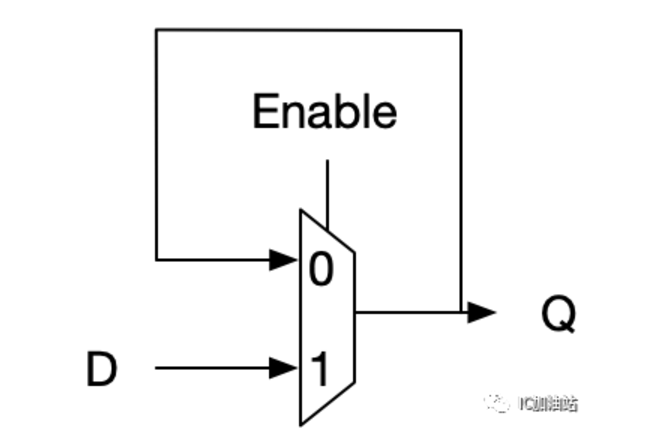
09 用2选1MUX搭Latch--难度3⭐️

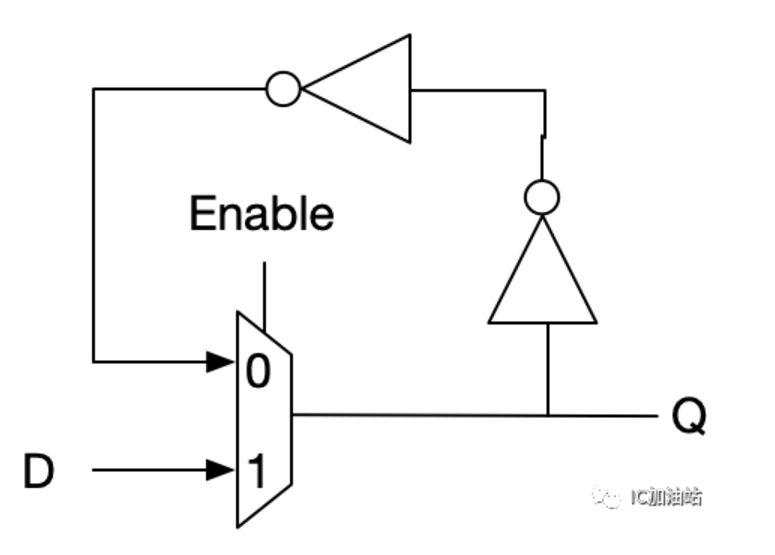
上面讲了那么多利用MUX来搭其他组合逻辑门电路，终于要来一个利用MUX来搭一个时序逻辑了。Latch是最简单的锁存逻辑门，Latch有一个Enable，当Enable为1的时候，Latch透明，输出Q等于输入D，当Enable为0的时候，Latch不透明，输出为之前锁住的值（这里说的是postive latch，如果是negative latch就刚好enable的值相反）。那么怎么利用MUX来锁住值呢？我们要利用反馈的方法，将输出反馈回输入。

注意，这里我们只是一个思维训练，即理论上可以利用MUX的反馈回去锁住一个值，但是实际工程中千万不要用这种方式去做一个latch，需要latch的时候请直接用厂家工艺库中提供的latch，原因有两点

MUX作为一个组合逻辑门电路，在STA分析中是不允许有反馈存在的，我们把这种violation叫做combo loop，因为STA分析针对combo cell的时序都是单向的，如果存在了一个反馈环路会导致这个路径没有终点！STA会报错的。
实际中的latch内部是需要两个back to back 的inverter，这样这两个inverter之间是正反馈，能够保证反馈是很快稳定的，而且当latch满足setup和hold的timing时，latch是可以保证锁住值的，这里的MUX由于不存在正反馈的反相器，实际仿真中如果enable不是理想切换，可能会导致锁不住值，所以更加稳妥一点的做法是

10 用2选1MUX搭D触发器--难度3.5⭐️

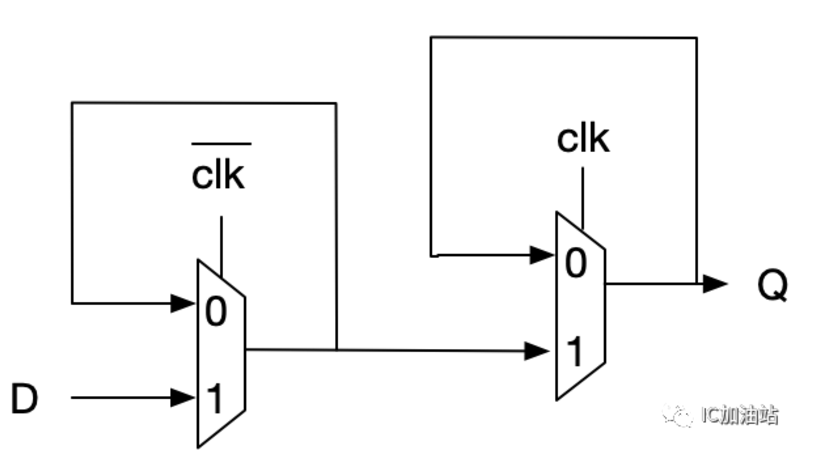
一般笔试题让你用MUX搭一个FlipFlop也就是到头了，这个其实也没有什么难度，考察你对D flipflop是不是理解。D触发器本质上是由两个latch组成，通常称作master slave latch，如下图所示

最后还有一类，是利用2选1MUX搭出4选1，8选1MUX，这个难度0.5颗星，老李就不放在这里了，相信大家都可以答上。

总结一下，面对这一类问题的思路就是，首先要熟悉目标电路的逻辑功能，可以熟练画出真值表，然后通常的做法就是将一个输入搭在MUX的S端上，这样可以将真值表对半分，然后再观察剩余部分的关系，还有很多情况那就再来一个MUX，继续分情况，总归可以出来规律。希望老李的这一篇基础内容可以帮助大家在面试的时候秒杀此类问题。