一.研究概述
在目标检测的以往研究和发展过程中,对于正负样本的定义和分配主要有两种方式
- 以Faster R-CNN为代表的,计算GT框和大量锚框之间的IOU来进行正负样本的取舍和分配,一般是以IOU大于0.7为正样本,IOU小于0.3为负样本,IOU大于0.3小于0.7的样本忽略不考虑。这种分配策略在后续的方法变种也非常实用和有效,但是这种固定策略仍然会因为各种大小、形状和类别的差异产生次优的结果。
- 根据数据分布的不同,自适应的划分生成锚框和划分正负样本。最近的许多工作,从ATSS,PAA到AutoAssign,都试图使标签分配更具有灵活性,但是这些方法只探索了单个对象的最优分配策略,并没有从全局的角度考虑上下文信息。换句话说,对于一张图产生的所有的检测框之间都是独立的没有联系。所以,对于处在两个交叠目标之间的模糊框而言,更多上下文的信息没有办法得到有效的处理和利用。这使得模型可能存在信息的偏差从而陷入次优。
所以对于基于CNN的检测器,一个能考虑全局信息分配正负样本的策略是必要的。为了解决这个问题,旷视提出OTA——一个专门进行标签分配的优化算法。OTA把标签分配视作最优传输问题,在GT和所有预测框之间计算运输成本,通过寻找一个合适的映射关系,使得运输成本最低。对于最优传输问题,我们在下一部分进行介绍。
OTA是第一个提出全局分配策略的方法,它可以同时插入一阶段和两阶段的检测网络,并可以获得不可忽视的性能提升。
二.最优传输问题
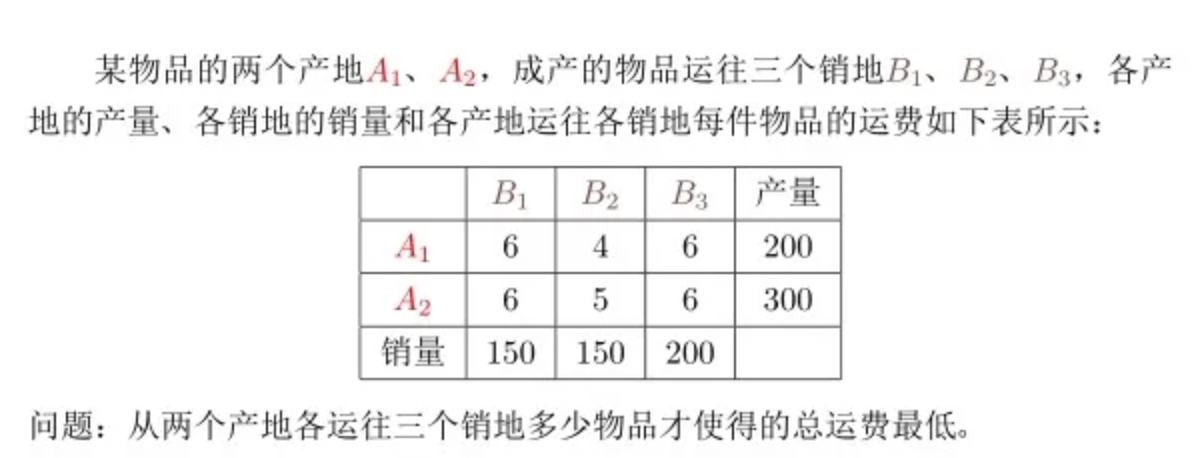
最优传输是多个学科交叉的研究领域,它的主要目标是建立有效比较概率分布的几何工具。对于OTA的分配方法,这主要基于最优传输理论中的wasserstein距离来建立模型的,那么什么是wasserstein距离?这里我们先举一个实际问题的例子:
所谓的wasserstein距离,从上述例子来看,就是“从产地运送物品到销地的最低成本”,而从概率分布的角度来看,是为了衡量了把数据从分布p”移动“成分布q时所需要移动的平均距离的最小值,这是在相同的度量空间上进行衡量的距离。
除此之外,最优传输理论中还有对不同度量空间的两种分布进行数据匹配的距离,今年我们在CVPR2021上投中的《DeepACG: Co-Saliency Detection via Semantic-aware Contrast Gromov-Wasserstein Distance》,就是通过Gromov-Wasserstein距离衡量一组图片的相似度,并匹配他们的特征,GW距离会避免由于图片风格、色差、对比度等不同所带来的噪声影响,对我们的任务起到相当关键的作用。
上述两种距离都可以通过sinkhorn算法进行优化求解,由于该论文主要涉及的是W距离,对于GW距离我们不再过多展开。很明显,W距离的原始模型就是一个天然的全局优化算法,每一个“产地”都会和每一个“销地”计算距离,并从中找到最优解。那么OTA为何并且又如何用W距离来进行全局分配,我们在下面具体展开。
三.OTA
从已有的目标检测的研究来看,对于所有预测框,都按照固定阈值进行舍弃,所以并不是每个有用的预测框都能被分配到gt标签。不考虑物体边缘的部分框和训练预热这两类情况,还有可能因为物体大小形状遮挡等外在原因而被划归为模糊框,其实这些特殊框正是能提高模型泛化能力的要素,可是由于在训练过程中采取暴力舍弃的手段,这些框并没有得到有效的利用,所以训练完成的模型泛化能力有限。因此我们不能过于依赖固定域值作为标准,应设计出一个能充分考虑全局的分配方法,尽可能涵盖到所有有效框。
为了解决上述的问题,论文引入了最优传输理论,认为GT标签和预测框之间的关系是一个运输问题。具体而言,作者首先为每个GT标签和背景标签分别设置了相应的权重,该权重是指该标签拥有多少单位的物品,注意,无论是GT还是背景,他们的权重都是不固定的,但这些权重之和恰好等于一张图片预测框的总个数。
由此把GT和背景视作供应端,把预测框视作需求端,每一个需求端都需要且仅需要一个单位的物品(即标签)才能运作,并且每一个供应端和需求端的距离(loss)不尽相同,从而建立最优传输数学模型,由于整个供求是平衡的,所以只要该GT标签拥有恰好的权重,其附近的“特殊框”就一定会被分配到该标签,那么这些原本被认为模糊的有效框就会得到利用。
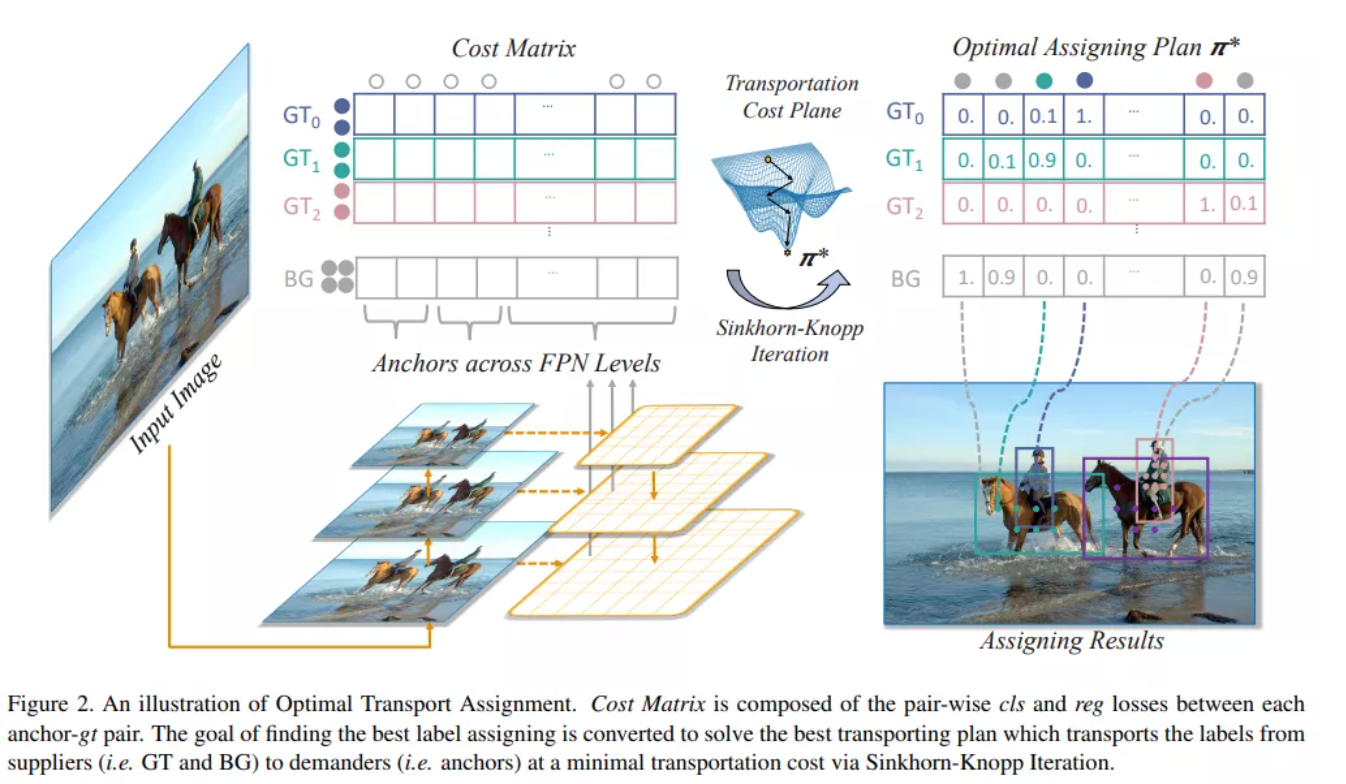
如Figure2分配结果所示,优化分配计划 趋向成为稀疏矩阵,优化过程中,初始化的分配矩阵会自然的把每一行每一列的权重集中在少数的位置上。它的每一行之和肯定等于该标签的权重,每一个标签都会依照预设的权重分配出去,不会像以往的方法那样为了追求暂时的最优使得部分预测框没被分配。而该矩阵的每一列之和都肯定等于1,通过max函数,每一个预测框都会被分配到一个更正确的标签。
该数学模型的设计主要有两个难点。1.供应端和需求端之间的距离(即loss),2. GT和背景标签所拥有的权重多少。首先是第一个问题,对于预测框和GT标签的loss。论文提出由三部分组成,其中两个是比较常用的,针对物体分类的Entropy损失和预测框相对位置的IOU损失,这两个loss还可以由focal损失、GIOU损失或者SmoothL1损失代替。其次,由于最优传输模型是可以在全局分配的方法,但是从经验上,GT标签只会分配给附近的预测框,而对于相对远的框,我们应该直接不考虑,所以为了加快最优传输模型的收敛和检测模型的稳定性,作者额外增加了一个针对GT标签的中心先验损失:对于不在一定范围r内的预测框,在前两个loss的基础上再增加一个常数作为惩罚项。其中,这个范围大小是个超参数。
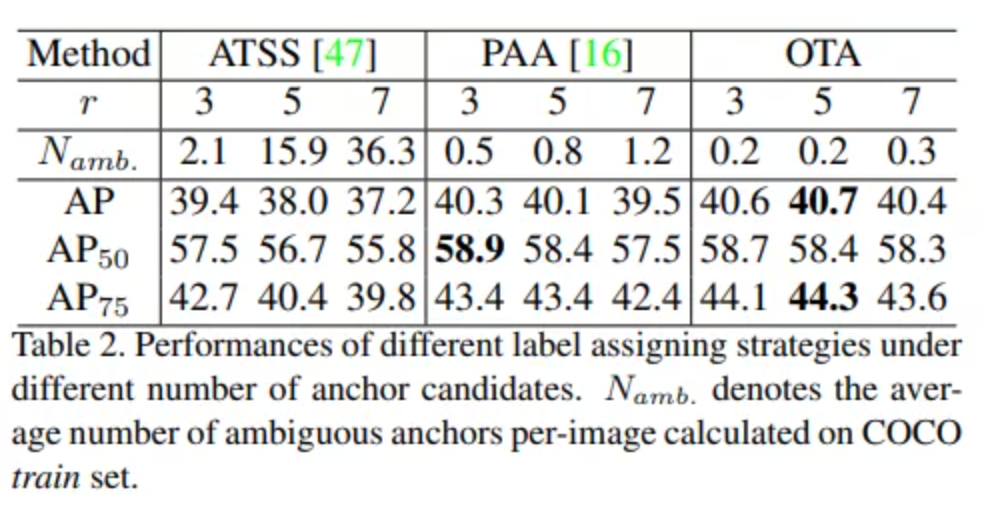
Table 2中进行了有关范围r和类似策略的消融实验,无论取3,5或7,OTA的性能都优于其他的策略,在合适的范围r里,OTA所判定的模糊框大大减少,这间接说明了减少模糊框的个数可以有效的提高模型的性能,但当r设为7时,模糊框的数量就会变多,性能也随之有一定程度下降,这说明强迫最优传输模型关注局部区域是有必要的。
第二个问题,如何给GT标签分配权重k。k的值代表一个GT标签会被分配给几个预测框。直接的方法是把k作为超参数进行预设,但是这样并不是最好的方法,每个GT框能够对应的预测框数量肯定是不同的,论文提出了一个折中的方案,首先取出最接近GT标签的前q个框,然后对所有IOU求和得出这些预测框相对该标签的期望值。很明显,期望越高,意味着有更多的预测框应该被标记成该GT标签,所以论文把GT标签的权重设置为该期望值。其中,q是个超参数,作者在多次实验后把它设置为20。
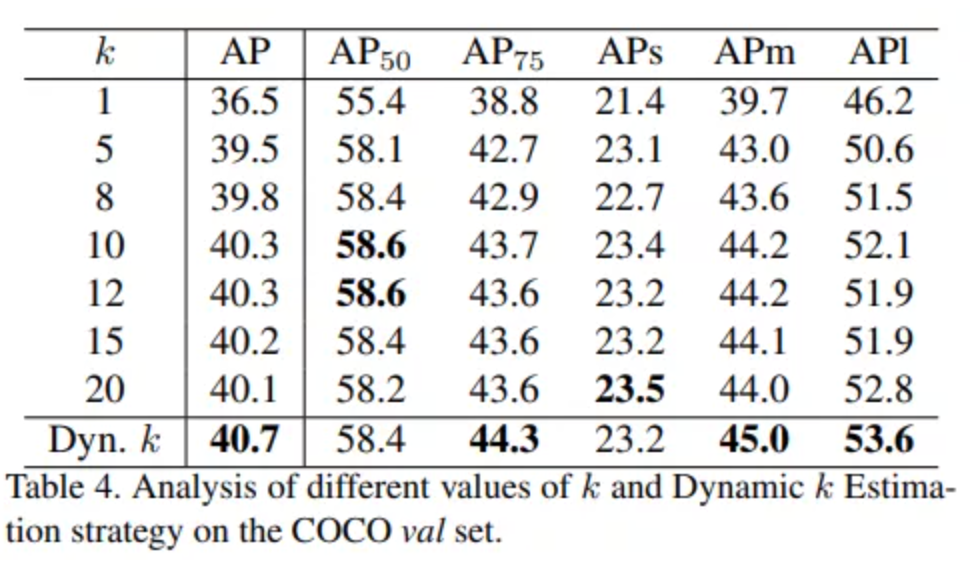
如Table 4 所示,如果权重k赋予固定的值,其对检测的提升是有限的,这是因为k不能对所有样本的都能起到同样的效果,而自适应的k则表现出其强势的性能。
四.结果
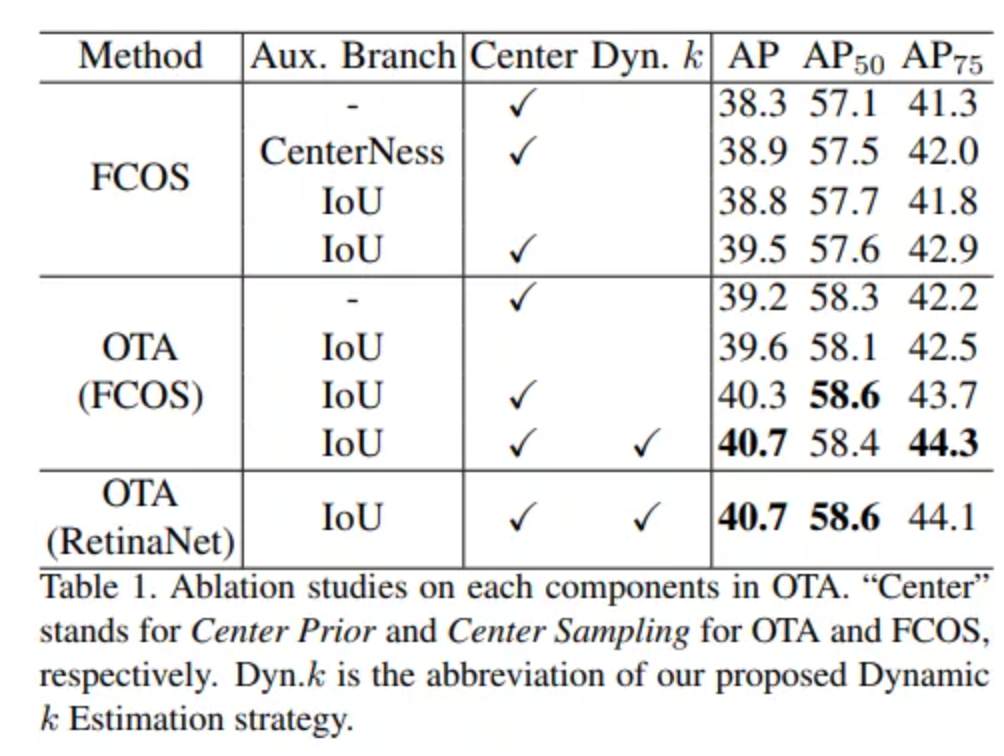
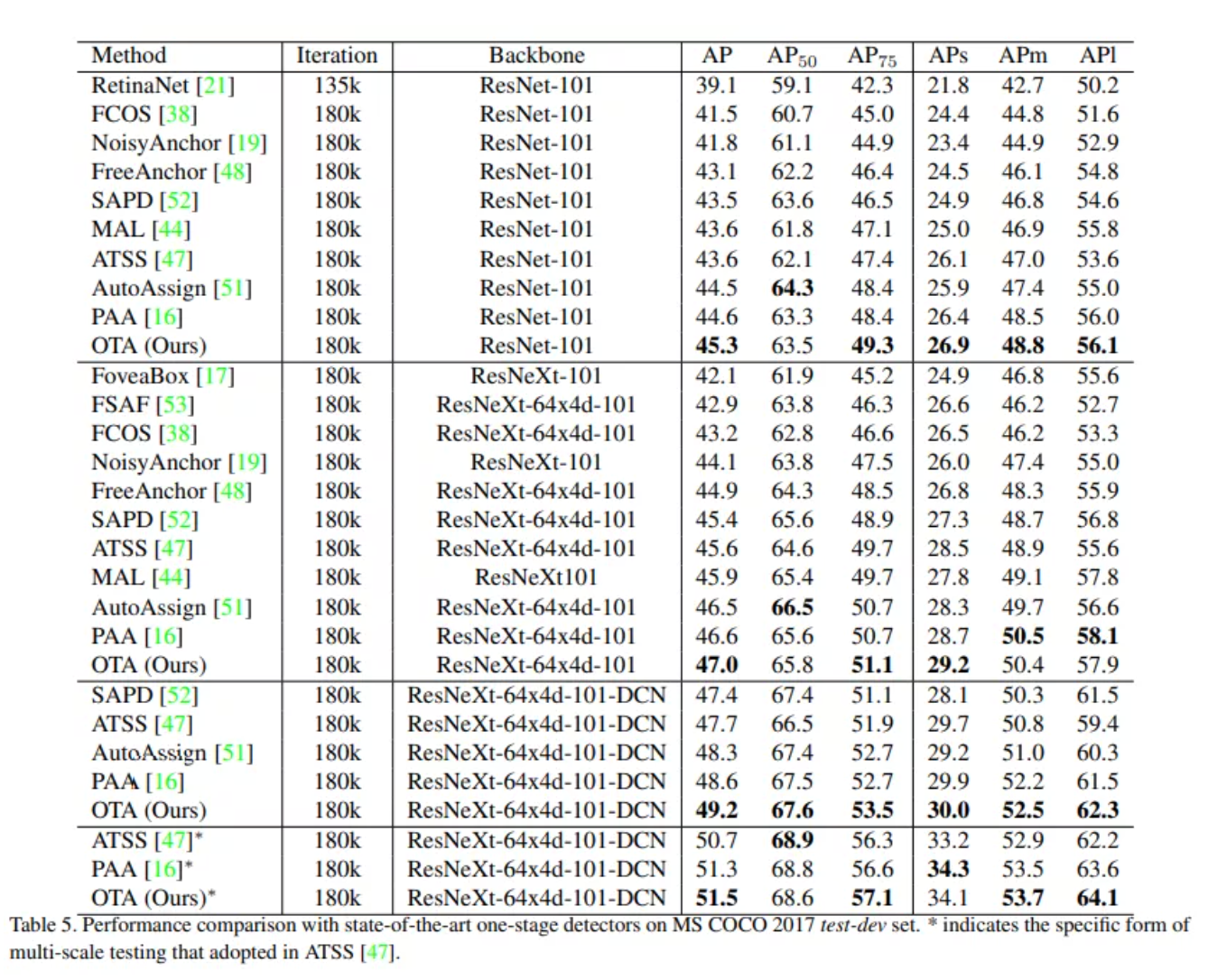
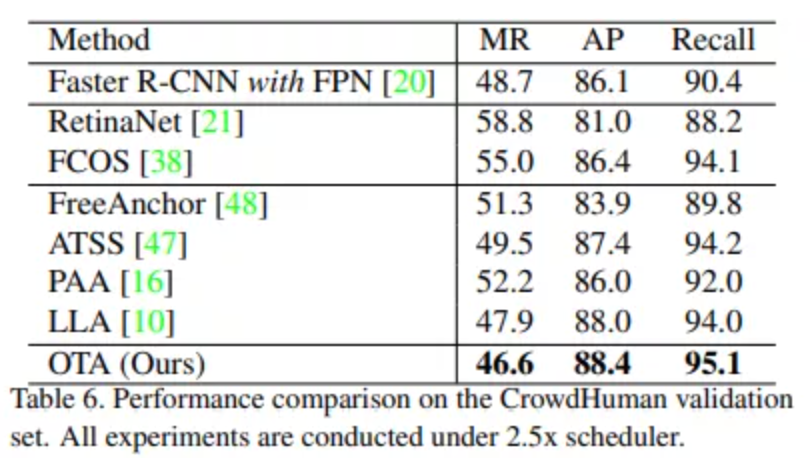
如Table1,5,6结果所示,OTA可以很容易插入一阶段和二阶段检测的方法,并且都展现不错的检测效果。对于不同的测试集,拥有OTA策略的方法超过了以往的方法,实现了SOTA。
五.结论和延申
OTA通过引入最优传输理论探索了全局分配标签的可能性,很大程度上减少了模糊框的个数,提高了训练数据的利用率。并且这种策略可以插入到的大部分的检测网络,可移植性强。不过由于sinkhorn算法的复杂度不容小觑,以及该数学模型存在从经验上预设的超参数,个人认为该策略仍然有非常大的改进空间和提升空间,并且如果能引入GW距离或者FGW距离建立一张图片所有gt标签的所隐含的结构信息、方位信息或逻辑信息(比如苹果在桌子上面,红色车遮挡了蓝色车),gt标签或许能更好被全局分配。
首发:旷视研究院
作者:葛政&董明亮
专栏文章推荐
欢迎关注旷视研究院极术社区专栏,定期更新最新旷视研究院成果
加入旷视:career@megvii.com