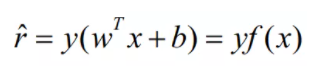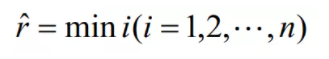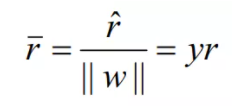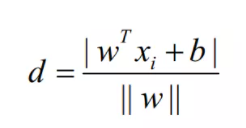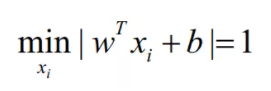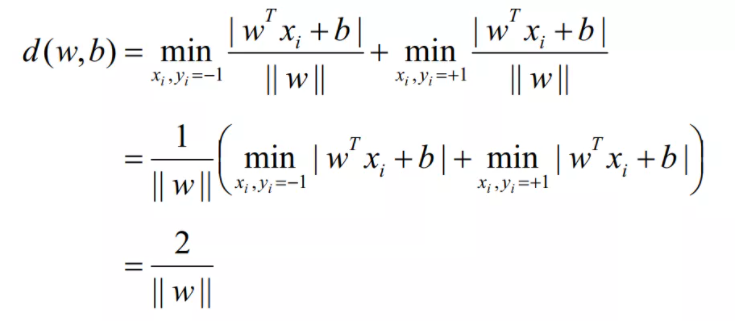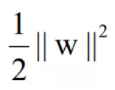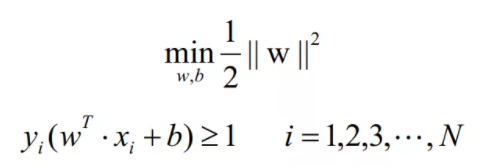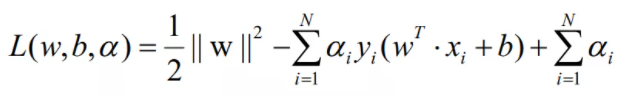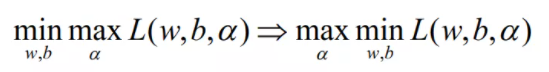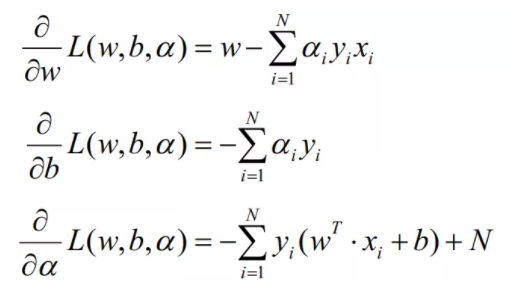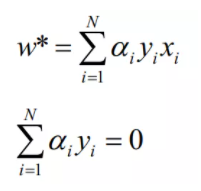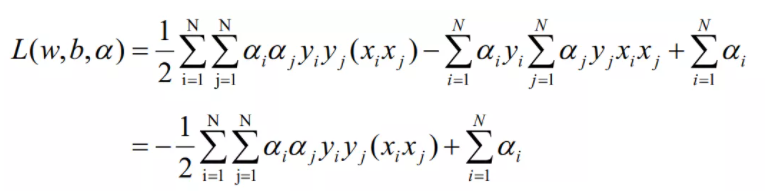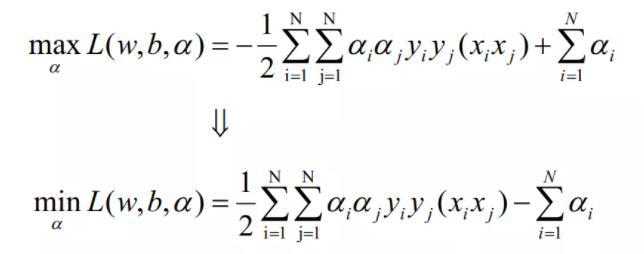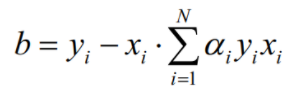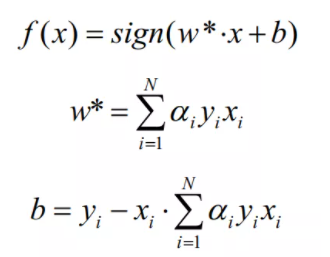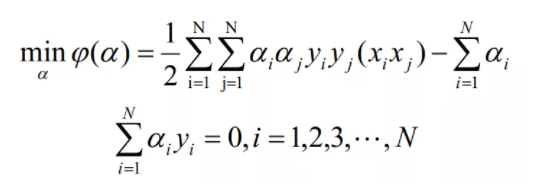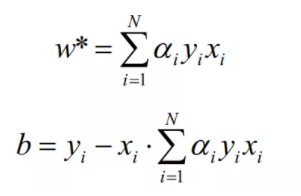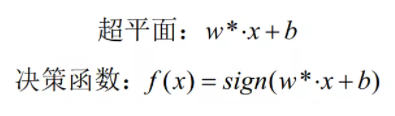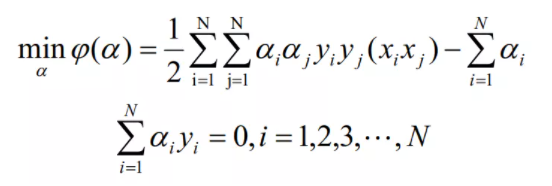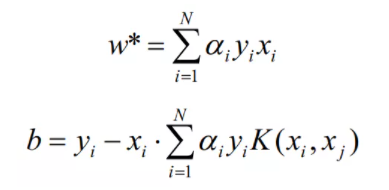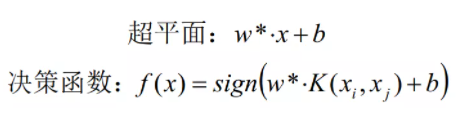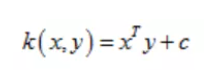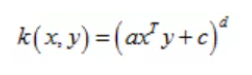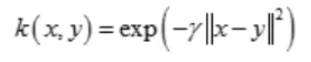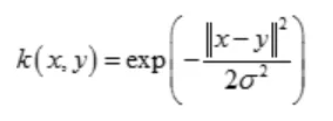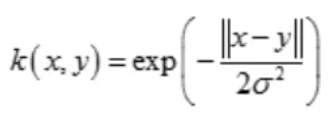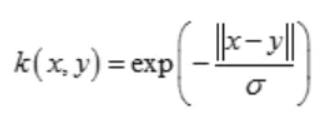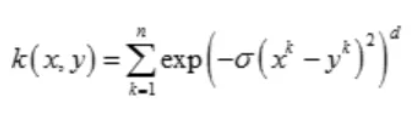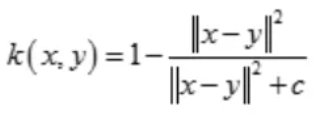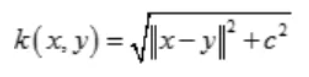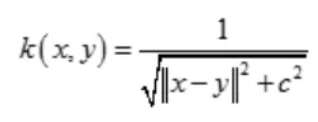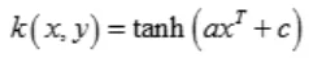简介
支持向量机(SVM)主要是用来解决数据分类的问题,而分类的目的则是构造一个分类函数或者分类模型,该模型能把数据库中的数据项映射到给定类别的某一类,从而可以预测未知类别。
支持向量机可以分为线性支持向量机(也称为硬间隔支持向量机)、非线性支持向量机(也称软间隔支持向量机)。主要的应用领域是文本分类、图像分类、数据挖掘、手写字符识别、行人检测、人脸识别等领域。
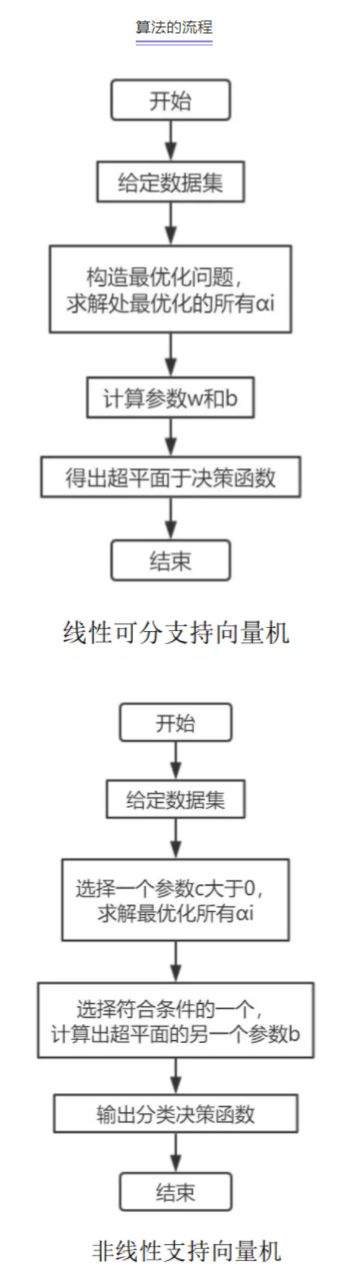
算法的流程
函数间隔于几何间隔
在超平面确定的情况下,|wx+b|可以表示点x到超平面距离的远近,而通过观察wx+b的符号于类标记y的符号是否一致可判断分类是否正确,所以,可以用决策函数的正负性来判定或表示分类的正确性。于是可以引出函数间隔的概念。函数间隔(用表示)的定义为:
超平面(w,b)关于T中的所有样本点(xi,yi)的函数间隔最小值(其中,x为特征,y是结果标签,表示第i个样本)便为超平面(w,b)关于训练数据集T的函数间隔:
但是,这样定义函数间隔存在问题,如果w和b成比例增加或者减小函数间隔且不变,但是实际超平面的间隔在发生变化,于是便提出了具有约束的函数间隔也就是几何间隔:
几何间隔也可以根据几何关系得到,这里不做过多说明。
算法具体步骤的推导
对于一个数据点进行分类,超平面离数据点的“间隔”越大,分类的确信度也就越大,为了使分类器的确信度尽可能地高,需要将所选择地超平面能够最大化这个“间隔”值。由前面的分析可以知道,函数间隔不适合用来做最大化间隔值,因此使用的使几何间隔作为优化的间隔。
1、线性可分SVM
由于要求超平面离两类样本地距离要尽可能大,根据点到平面的距离公式,每个样本点到超平面的距离为:
其中||w||为向量的L2范数,在这里超平面与样本之间是存在冗余的,所以在这里利用这个特点简化求解问题,对w和b加上如下的约束:
可以消除这个冗余,同时简化点到超平面距离的计算公式。
于此可以写出两类样本到超平面的距离间隔为:
目标是使得间隔最大化,这样的话上式的结果等价于最小化如下的目标函数:
于是间隔最大化问题可以对偶为最小化如下的问题:
可见上式就是一个带不等式约束的最优化问题,可以构造拉格朗日函数进行求解,所构造的拉格朗日函数如下:
在此引入拉格朗日的对偶问题,即:
先对于L(w,b,α)求关于参数的导数,分别如下:
由对偶后先求解min问题,即令w,b的偏导数为0,求出极值条件下的值:
将导数代入拉格朗日函数得到:
于是优化问题也变成了
因为wx+b=yi,代入w*的值,可以得到b为:
于是可以得出决策函数为
综上所述,线性可分支持向量机的算法步骤如下:
(1)给定数据集T={(x1,y1),(x2,y2),(x3,y3),...,(xN,yN)},y={+1,-1};
(2)构造最优化问题:
求解最优化的所有α
(3)计算参数w*和b
(4)得出超平面与决策函数
2、非线性SVM
在线性不可分的情况下,支持向量机首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维空间,最终在高维特征空间中构造出最优分离超平面,从而把平面上本身不好分的非线性数据分开。
下面直接给出非线性支持向量机算法的步骤:
综上所述,线性可分支持向量机的算法步骤如下:
(1)给定数据集T={(x1,y1),(x2,y2),(x3,y3),...,(xN,yN)},y={+1,-1};
(2)构造最优化问题:
求解最优化的所有α
(3)计算参数w*和b
(4)得出超平面与决策函数
3、常见的核函数
(1)线性核(Linear Kernel)
(2)多项式核(Polynomial Kernel)
(3)径向基核函数(Radial Basis Function)
也叫高斯核(Gaussian Kernel)
(4)幂指数核(Exponential Kernel)
(5)拉普拉斯核(Laplacian Kernel)
(6)ANOVA核(ANOVA Kernel)
(7)二次有理核(Rational Quadratic Kernel)
(8)多元二次核(Multiquadric Kernel)
(9)逆多元二次核(Inverse Multiquadric Kernel)
(10)Sigmoid核(Sigmoid Kernel)
以上几种是比较常用的,大部分在SVM,SVM-light以及RankSVM中可用参数直接设置。还有其他一些不常用的,如小波核,贝叶斯核,可以需要通过代码自己指定。
SMO最小序列算法推导(部分)
全部推导内容见我的csdn博客:
https://blog.csdn.net/qq\_24819773/article/details/86513166
SVM算法的优缺点
优点:
1、使用核函数可以向高维空间进行映射;
2、使用核函数可以解决非线性的分类;
3、分类思想很简单,就是将样本与决策面的间隔最大化;
4、分类效果较好;
缺点:
1、对大规模数据训练比较困难;
2、无法直接支持多分类,但是可以使用间接的方法来做。
PCA算法的改进和优化
1、最小二乘SVM(LS-SVM)算法
LS-SVM是SVM的一个变体。它从机器学习损失函数入手,在其优化的目标函数中使用二范数,并利用等式约束条件代替SVM标准算法中的不等式约束条件,使得LS-SVM方法的优化问题的求解最终变为一组线性方程的求解。
传统SVM中,约束条件是不等式,离分离超平面近的元素向量是支持向量,强烈影响分离平面的计算,离超平面远的向量影响比较小;因此如果分离集合之前的边界不清晰,会影响计算结果。而LS-SVM中约束条件是等式,因此,离分离超平面无论远近都对分离超平面有影响,不过分离超平面不如传统的SVM精准;而且一旦产生相当数量的大的离群点,会严重影响分离超平面的计算。LS-SVM的最终结果,近似于将两个分离集合的所有元素到分离平面的距离都限定在1+n,n是可接受误差;
LS-SVM方法通过求解线性方程组实现最终的决策函数,在一定程度上降低了求解难度,提高了求解速度,使之更适合于求解大规模问题,更适合于实际问题,虽然不一定能获得全局最优解,但仍可获得较高的识别率;
2、概率SVM
概率SVM可以视为Logistic回归和SVM的结合,SVM由决策边界直接输出样本的分类,概率SVM则通过sigmoid函数计算样本属于其类别的概率。具体地,在计算标准SVM得到学习样本的决策边界后,概率SVM通过缩放和平移参数对决策边界进行线性变换,并使用最大似然估计得到结果,将样本到线性变换后超过超平面的距离作为sigmoid函数的输入从而得到概率。
SKlearn算法的实践
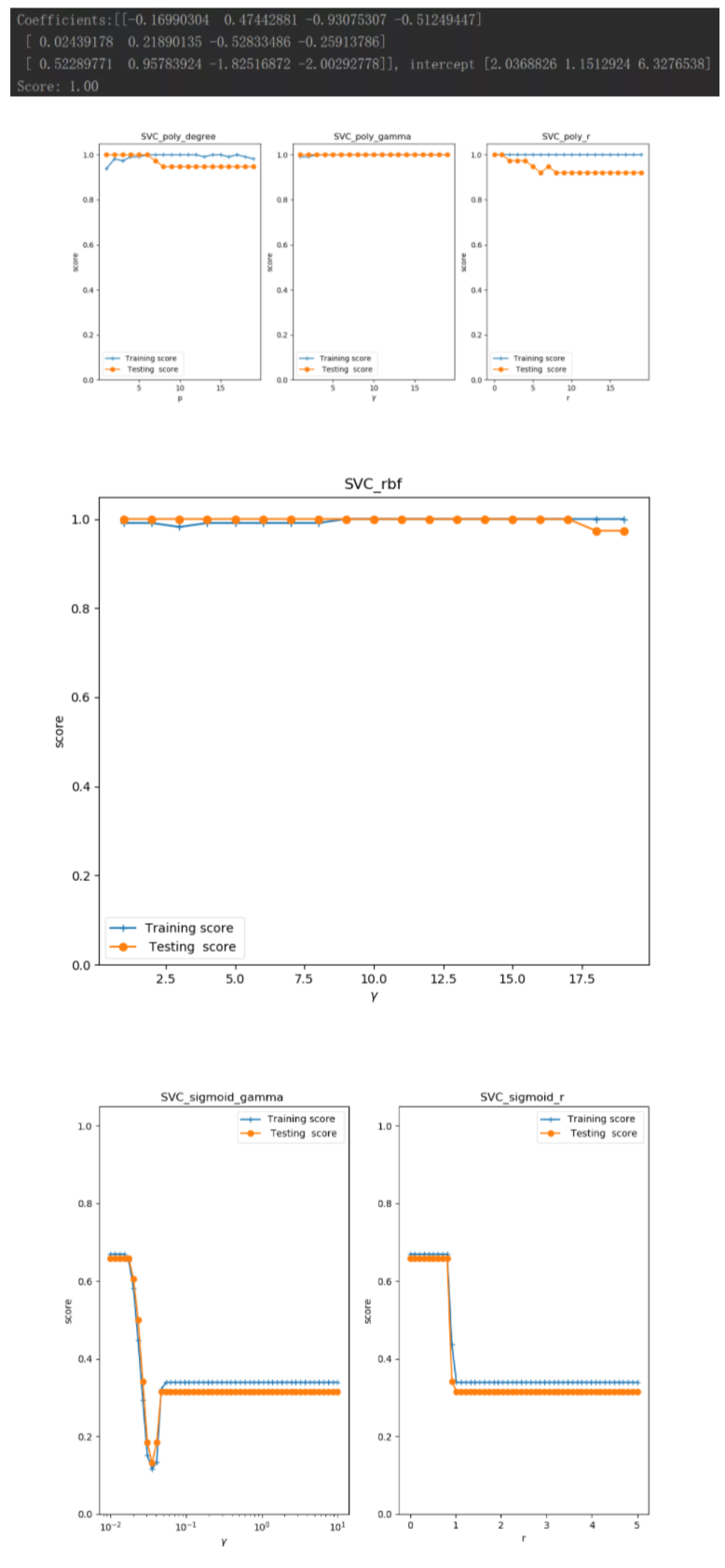
SVM算法实践
执行结果:
文章转载于:集智书童
作者:ChaucerG
推荐阅读
更多嵌入式AI技术相关内容请关注嵌入式AI专栏。