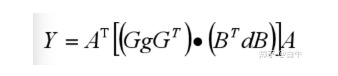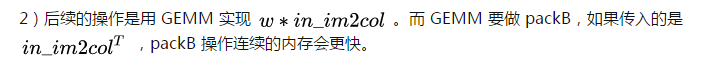前言
本文以各开源项目为例,讲解 arm CPU 平台上卷积计算方法。最后结合卷积(业务)提出一项简单的加速方式。作为三年的忠实 ncnn 伸手党,此方法已 merge 到 ncnn。
具体的实现虽然千变万化,但在目前金字塔型存储结构下,加速原则一直没变过。
目录
一、direct
二、winograd
三、im2col 和 im2row
四、不适合手机场景的方法
五、通用优化思路
阅读前提
本文假定读者:
一、Direct Conv
所谓 Direct,顾名思义就朴素地直接计算。下面的代码是个朴素地卷积计算代码块:
for (x = 0; x < r; x++)
{
for (y = 0; y < c; y++)
{
for (i = 0; i < m; i++)
{
for (j = 0; j < n; j++)
{
q = x;
w = y;
B[x, y] = B[x, y] + (Rep[i + q, j + w] * h[i, j]);
}
}
}
}Direct 与这种 for 循环的区别在于:
- 会根据参数做特化,例如 kernel1x1 写一版、kernel 3x3 写一版...这样可以节省一些下标计算用的乘法操作,特定尺寸有特定优化技巧;
- 会使用硬件平台特性,在 arm 上就是 neon 指令集。
Direct 方法优点在于特定尺寸速度极快,接近极限;缺点在于代码膨胀,开发工作是个力气活,不适合人力短缺的团队。我们以 conv1x1s1 和 dwConv3x3s1 为例。
conv1x1s1
已知 GEMM 是 AB 矩阵在 k 维度点乘累加,
又知当 kernel=1 pad=0 stride =1 dilation=1 时,卷积计算是在 input_channel 维度点乘累加,
所以此时 conv1x1 可以转化为一个 GEMM,其中:
k = input_channel
m = output_channel
n = input_h * input_w
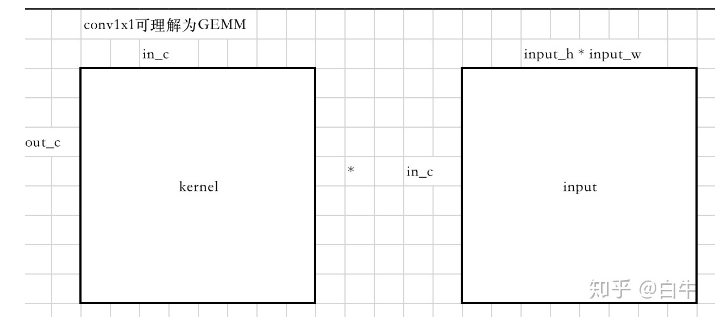
卷积权重看做 m*k 的矩阵,输入看做 k * n 的矩阵。画成图就是这个样子:
conv1x1可理解为GEMM
后面就是 GEMM 的计算拆分,我们以 ncnn conv1x1 为例:
...
const float* kernel0 = kernel + (p+0)*inch;
const float* kernel1 = kernel + (p+1)*inch;
const float* kernel2 = kernel + (p+2)*inch;
const float* kernel3 = kernel + (p+3)*inch;
const float* kernel4 = kernel + (p+4)*inch;
const float* kernel5 = kernel + (p+5)*inch;
const float* kernel6 = kernel + (p+6)*inch;
const float* kernel7 = kernel + (p+7)*inch;
float* ktmp = kernel_tm.channel(p/8);
for (int q=0; q<inch; q++)
{
// kernel0...7 0
ktmp[0] = kernel0[0];
ktmp[1] = kernel1[0];
ktmp[2] = kernel2[0];
ktmp[3] = kernel3[0];
ktmp[4] = kernel4[0];
ktmp[5] = kernel5[0];
ktmp[6] = kernel6[0];
ktmp[7] = kernel7[0];
ktmp += 8;
kernel0 += 1;
kernel1 += 1;
kernel2 += 1;
kernel3 += 1;
kernel4 += 1;
kernel5 += 1;
kernel6 += 1;
kernel7 += 1;
}
}
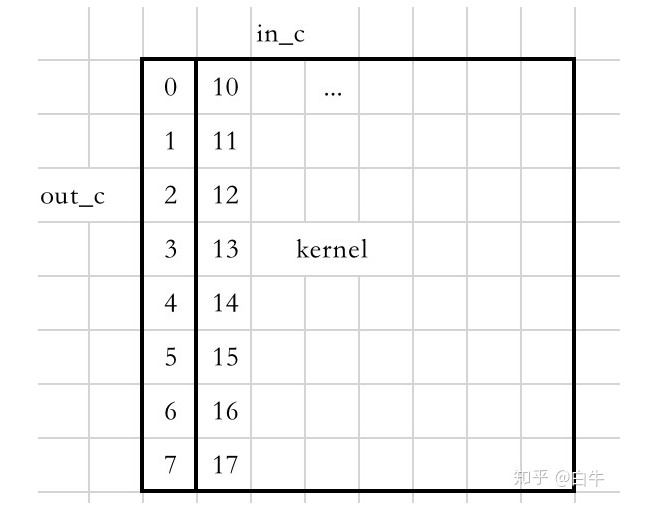
...要做的操作其实就是先对 kernel 做 PackA,一次最多操作 8 行,如下图顺序。
packA
可以推断出后续要对 input 做 packB,同样一次性最多做 8 列,最后 sub\_kernel。这里不再赘述,可参照 GEMM 从零入门 ,也可看后续的 im2col + GEMM 的方法。
dwConv3x3s1
Tengine 的实现比较巧妙:卷积的每一行可以看做 1*w 大小的 vector 不动,1*3 的 kernel 在向右滑动点乘累加;也可以看做 1*3 的kernel不动,1*w 大小 vector 在向左滑动累加。
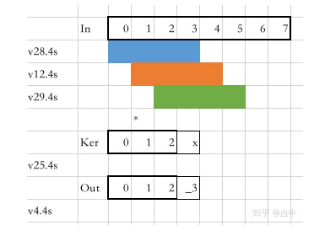
kernel不动,input向左滑动
v28.4s 填装 In0-In3,v12.4s 放In1-4,v29.4s 放 In2-In5。 v25.4s 存放 kernel 的一行,末尾的 32bit 废弃不用。三个输入分别和 v25.s[0]、v25.s[1]、 v25.s[2] 做向量-矢量乘法并累加到 v4.4s。运算结束后 v4.s[0] 刚好是最终的输出。
相关的代码可见
ld1 {v12.4s},[x0],#16
ld1 {v13.4s},[x0]
// 用 ext 指令做拼接,准备输入
ext v28.16b,v27.16b,v12.16b,12
ext v29.16b,v12.16b,v13.16b,4
// 三次矢量-标量累加乘即得到 3 个结果
...
fmla v4.4s,v28.4s,v25.s[0] //k10,
...
fmla v4.4s,v12.4s,v25.s[1] //k11,
...
fmla v4.4s,v29.4s,v25.s[2] //k12目前挂在 github 上的 Tengine 仍是阉割版,商业版本需要联系 OAL。
二、winograd
论文见 Fast Algorithms for Convolutional Neural Networks 。
商业互吹 Int8量化-Winograd量化原理及实现(四)。
中国剩余定理和 winograd 关联关系见 源于《孙子算经》的Cudnn。
相关文章已经很多,这里就简单过一下 F(2,3) 计算过程:
- 先把输入拆成多个 4x4 的 block,stride 2;
winograd公式
2. 上述公式里 A/G/B 都是常量矩阵,g 是 3x3 大小的权重,d 是拆出来的 block。
费老鼻子劲搬数据转成 GEMM 计算有啥好处?
直接用现成的 GEMM 库省事儿,具体省了哪些事?
winograd 算法本身有矩阵转换的成本,计算量较大时(例如 VGG16)才能发挥出效果。计算量大的时候,一般参数也很多,此时需要考虑 cache 命中率。刚好 OpenBLAS 等很早就做了 cache 上的优化,因此费点功夫把数据调整成适合 16 次 GEMM 的布局,效果要好于直接按公式实现。
ncnn 最新的做法是用 nc4hw4 布局,nchw 前提下得出的结论已经不适用。
三、im2col+GEMM
caffe 的方法
im2col 排布方式见caffe im2col 详解,里面讲得已经很细致。
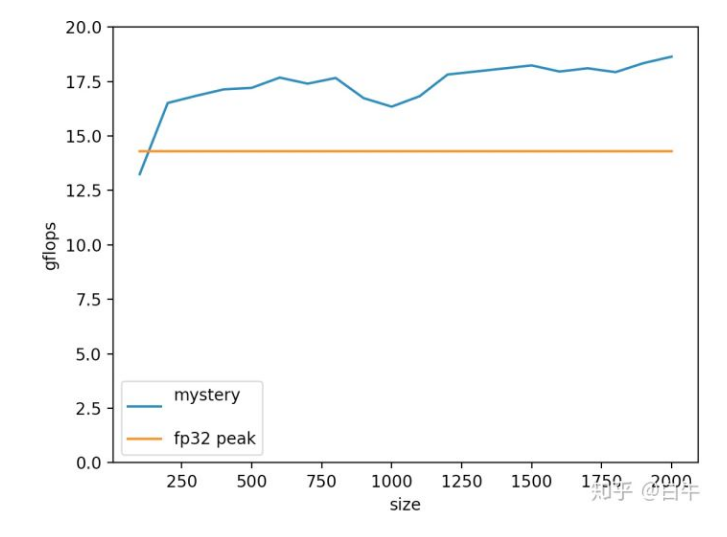
关于第二步的 GEMM,本座开源了一个 armv8 的 int8 gemm 小项目,名叫 chgemm (意为 char GEMM)。在 rk3399 上 gflops 如下。
横轴是 GEMM MNK 大小,纵轴是 gflops。橙线是 rk3399 fp32 理论极限 14.3gflops。
chgemm 有两个提速点:
- 使用 kernel4x8,用 smull 一次操作 8 个 int8\_t;
- 输入不能是 -128,可以避免一次 sadalp 指令。
目前最高可到 18.6 gflops,还有 5% 左右的提升空间。
im2col 和 im2row
为什么 im2row 是更好的方法?
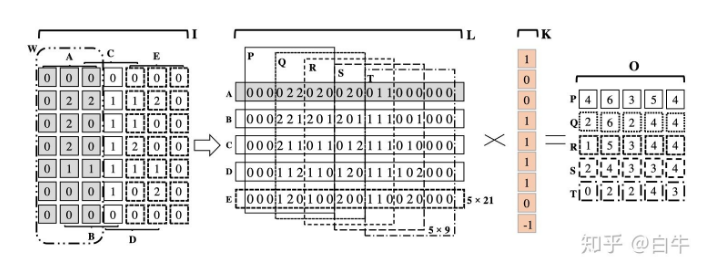
1)通用(不考虑特化版本)的 im2col 操作一次把 kernel*kernel 大小的输入展开成一列。在行主序的程序里,按列保存是低效的;
四、不适合手机场景的方法
MEC 论文
MEC
MEC 本质上是只做了 h 维展开的 im2col 方法。的确可以节省内存,计算效率不高。
手机 APP 要考虑发热、耗电问题,多线程是不可能多线程的,外加常用 kernel是 3x3,因此 FFT 难以在手机上用起来。
五、手工优化思路
本座不是搞优化出身,摸索了 3 年的模型落地,总结了一个通用的优化过程:
- 一个优化任务过来,先看目标硬件上的理论极限是多少。这个测试方法可参照部分 git 代码。例如在 rk3399 上单核是 14.3 gflops;
- 然后估算这个任务要做多少次乘加,例如是 28 g macc。此时就知道了即便做到 100% CPU使用率,也需要 2s 才能算完。考虑到工期和乱七八糟的额外计算,能发挥 90% 已经很不错了;
- 然后看优化到 100% 使用率能否满足客户需求。一般是不满足的,而且理想和现实会差几倍;
- 既然不满足,就不要着急做,先沟通个能满足的方案出来。具体的方式因项目而异,例如:1)定点化 2)多线程 3)改模型 ... 总之更是个沟通的活儿而非搬砖的活;
- 平衡工期、预期和实用场景,切忌像个没头苍蝇一样上手就做。
文章转载于:知乎
作者:白牛
推荐阅读