科学计算中的“科学”是AI for Science与AI的本质区别。与CV/NLP等经典领域不同,科学计算背后是一只有形的手,从定义、公理、推论到公式、模型、方程,这些以数学语言为基础的神秘力量在背后操纵着自然界和工程科学的各个领域。从这个角度上讲,在AI科学计算中丢弃“科学”当然是失智之举。AI for Science绝不仅仅是把AI应用于科学计算领域,而是两者相互影响与耦合,最终同时促进这两个领域的发展。
为了避免宽泛,本文仅讨论上述问题的一个侧面,即AI如何与“科学”相互协作最终解决科学计算问题,而“科学”对AI的启发从而改进其在CV/NLP等领域的应用则有机会另文再表。另外在文中以下部分,关于“物理”与“科学”的描述等价,仅表示问题的内在抽象或约束。
言归正传,AI科学计算领域有下面一张著名的图(见图一)。该图从数据和物理两个维度给出了AI科学计算的三种典型方法,从中也可以看出物理之于AI的重要性。实际上,即使背靠海量的数据,如果进一步引入物理,对其泛化性尤其是外插能力的提升同样具有重要推动作用。至于如何引入物理,学术界存在“physics-informed/physics-guided/physics-encoded/physics-constrained”等各种描述,本文对上述词汇不做区分,我们只关注physics是如何inform/guide/ encode/constrain的?下面我们分别从AI和科学计算的视角解答这个问题。

图一 AI for Science三种典型范式
AI视角
从AI视角来观察,意味着问题求解的主要工作由AI来承担。基于这种方式,物理的角色更像是重在参与,重在启发的斜杠青年。这种参与或者启发从前往后可以是如下几种方式:physical feature、physical architecture以及physical loss.
1.1 physical feature
在这种模式下,可以通过物理直接确定AI网络的部分输入,或者在AI模型中利用物理生成适当的特征图。
图二 单摆
除了对输入进行降维,物理还可以为AI网络提供特征。在科学计算中,通常通过数值仿真获取物理方程的解答,因此可以将数值仿真(可微求解器)内嵌作为AI网络的局部组件,从而生成近似满足物理约束的特征。基于这种思路,Belbute-Peres等人提出混合神经网络方法(见图三),通过在图卷积神经网络中内嵌可微流体仿真求解器SU2(数值仿真在更粗的网格下进行),结果表明该方法相比于单纯数据驱动的AI方法具有更好的泛化性,此外由于数值求解值在粗网格上进行,仿真性能仍然显著低于高保真度的传统数值仿真方法。
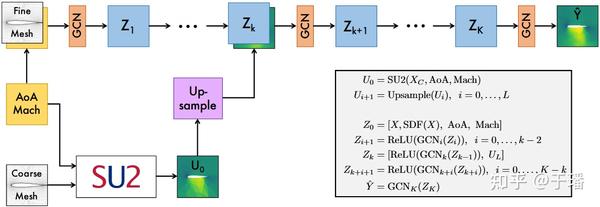
图三 GCN混合神经网络
1.2 physical architecture
物理现象背后的规律以及物理建模过程都可以对AI网络的设计产生启发。下面我们以MultiScale网络以及TF-Net网络为例介绍上述两个思路
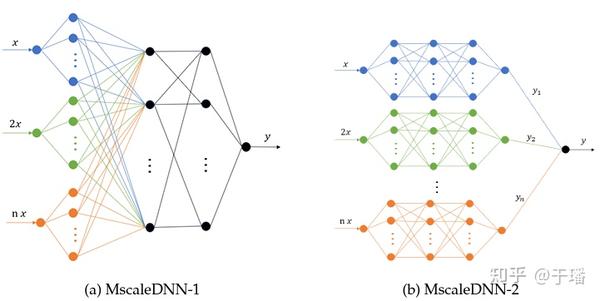
图四 多尺度神经网络
Multi-Scale网络(见图四)设计是建立在物理问题的“频率原则”之上。对AI而言,神经网络倾向于优先拟合目标函数的低频部分。而对于物理问题而言,其控制方程一般为微分方程的形式用于描述局部行为的变化,在求解过程中也可以发现问题的解通常是由局部逐步收敛到全局,也就是说物理问题是高频信息优先收敛到准确解。因此,为了让神经网络能够快速准确的捕捉各尺度的信息,避免高频学习慢的问题,可以对输入的各频率成分进行不同程度的放大,缩小频率差异避免相互竞争,从而降低问题学习的难度。
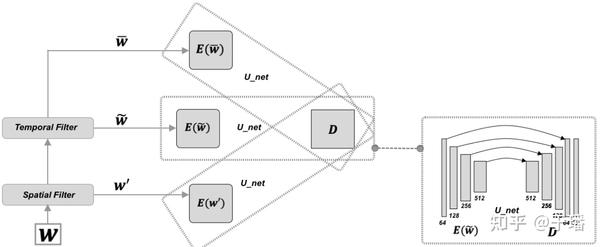
图五 TF-Net湍流仿真
1.3 physical loss
将物理约束引入神经网络的损失函数中是最为自然的做法。PINNs定义了物理信息神经网络的基础框架(见图六),它借助于AI框架的自动微分能力,将物理方程的残差加到神经网络的损失函数中,从而使得训练的结果满足物理规律。通过这种方式也可以作为监督数据损失函数的正则项,因此除了像传统神经网络一样学习到训练数据样本的分布规律,该方法还能够学习到数学方程描述的物理定律,从而弥补数据的不足并改进泛化性。
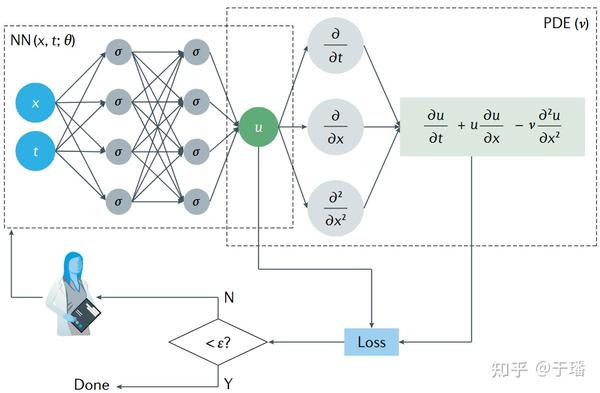
图六 物理信息神经网络
科学计算视角
此处所说科学计算视角的含义是,问题求解的主要部分是科学计算的传统处理方法,AI仅用于替代其中某些部分。从这个意义上讲科学计算与物理的结合主要有解耦与耦合两种模式。
所谓解耦,就是说AI网络的训练过程与科学计算独立。在AI科学计算的求解阶段,科学计算的某些过程仅需要调用AI网络的推理过程即可。这类方法在流体仿真中广泛采用,一方面可以用于处理湍流仿真的未封闭问题来提升RANS或者LES的模型精度,另一方面可用于学习壁湍流的近壁模型从而显著降低解析壁面的计算网格量。
AI与科学计算的耦合则意味着AI网络的训练与科学计算相互耦合同时进行。实现整个过程的前提条件是科学计算本身是端到端可微的。以流体仿真为例,Google的JAX-CFD以及慕尼黑工业大学的PhiFlow是学术界最受关注的AI与CFD耦合的仿真工具。两者均是基于AI框架开发的计算流体力学求解器,只是AI与CFD耦合的方式有所不同(JAX-CFD被称为learning-interpolation, PhiFlow则是learning-correction),下面仅对JAX-CFD展开介绍
JAX-CFD learning-interpolation
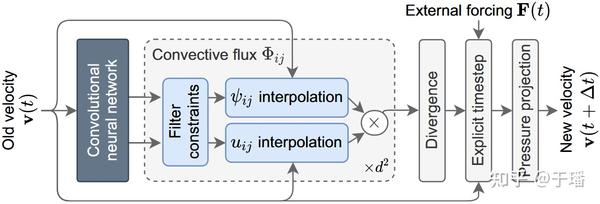
图七 JAX-CFD learning interpolation
JAX-CFD通过神经网络学习插值系数来重构NS方程离散求解过程中的非线性动量通量,在二维湍流仿真中该算法可以在各维度的分辨率粗糙 10 倍的情况下仍然可以逼近直接数值模拟的结果,并实现近两个量级的性能提升。该模型学习如何对解的局部特征进行插值,从而能够准确泛化至不同的流条件。
本文主要讨论了AI科学计算领域,物理(或者科学)跟AI相融合或启发的几种典型的模式,随着该领域研究的蓬勃发展,相信更多创新性的想法会不断涌现。因笔者认知有限,所述难免有所谬误和遗漏,欢迎各位读者批评指正。
来源:知乎
作者:于璠
推荐阅读
- MindSpore AI科学计算系列(16):分子对接基础
- Efficient Hyperparameter Tuning:解决大模型超参调优的难题
- MindSpore AI科学计算系列(13):蛋白质结构预测训练推理全流程开源,助力生物医药发展
更多嵌入式AI技术相关内容请关注嵌入式AI专栏。欢迎添加极术小姐姐微信(id:aijishu20)加入技术交流群,请备注研究方向。




