这篇文章通过一个实际的例子简要介绍了因果推理,这个例子来自于《The Brave and True》一书,我们使用 CausalPy 来实现。
因果推理是从观察数据中估计因果效应的过程。对于任何给定的个体,我们只能观察到一种结果。另一种结果对我们来说是隐藏的。这就是所谓的反事实(即与事实相反)。例如,我们可以干预或不干预病人,但我们只能在一种情况下得到结果。另一种结果是我们没有观察到的,因此被称为潜在结果。如果我们有一个没有接受干预但与接受干预的组非常相似的对照组,就可以估计潜在的影响。这里就要求必须确保两组在干预前没有任何差异。
合成控制法:Synthetic Control
在许多情况下,我们没有对照组来比较。比如我们向一定比例的用户展示广告。在广告曝光(即处理)之前和之后,我们记录到网站的流量。根据因果效应的定义,我们需要知道如果用户没有接触到该广告,会发生什么。在广告中,我们可以曝光一定比例的用户,而将其余用户作为对照组。
但是在下面的示例中,这是不可能的。
比如说,我们想知道限制吸烟的政策对香烟销售的影响。在这种情况下没有自然对照组,这就带来了一个问题,很难验证该政策是否真的对销售产生了影响。
这正是合成控制进入阶段的地方。这个想法是这样的:因为没有一个自然的对照组,所以只能尝试构建一个尽可能与干预组相似的对照组。在上面的例子中,我们可以使用其他类似省的数据。
import causalpy as cp
import pandas as pd
cigar = (pd.read_csv("data/smoking.csv")
.drop(columns=["lnincome","beer", "age15to24", "california", "after_treatment"]))
我们导入CausalPy Python包,加载数据并删除一些我们不需要的列。从美国39个不同的州获得了31年的数据。干预(政策开始)发生在1989年。加州是第一个州。在将数据传递给CausalPy之前,我们必须进行一些预处理工作,最还要把数据变成宽表的格式
piv = cigar.pivot(index="year", columns="state", values="cigsale")
treatment_time = 1989
unit = "s3"
piv.columns = ["s" + str(i) for i in list(piv.columns)]
piv = piv.rename(columns={unit: "actual"})
这样每个州就变成一列,每年一行。
formula = "actual ~ 0 + " + " ".join(list(piv.columns.drop("actual")))上面我们构建了一个公式,表示我们想用其他州的香烟销售来解释“实际”变量(即加州的香烟销售)。这里必须重命名列,因为不能使用整数。第一个0仅仅表示我们不想在模型中包含截距。
result = cp.pymc_experiments.SyntheticControl(
piv,
treatment_time,
formula=formula,
model=cp.pymc_models.WeightedSumFitter(
sample_kwargs={"target_accept": 0.95}
),
)上面的代码创建了模型并进行适配。我们只需要将数据连同干预时间和公式一起传递给CausalPy。上面该公式描述了我们想要如何构建合成控制组(即哪些变量)。除了使用SyntheticControl作为我们的实验类型外,我们还告诉CausalPy想要使用WeightedSumFitter作为我们的模型。
结果
CausalPy在运行时将启动一个马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)算法,算法通过从后验分布中提取样本来执行推理。我们在这里不深入贝叶斯推理的细节,因为以前已经有文章直观地解释了这个概念。
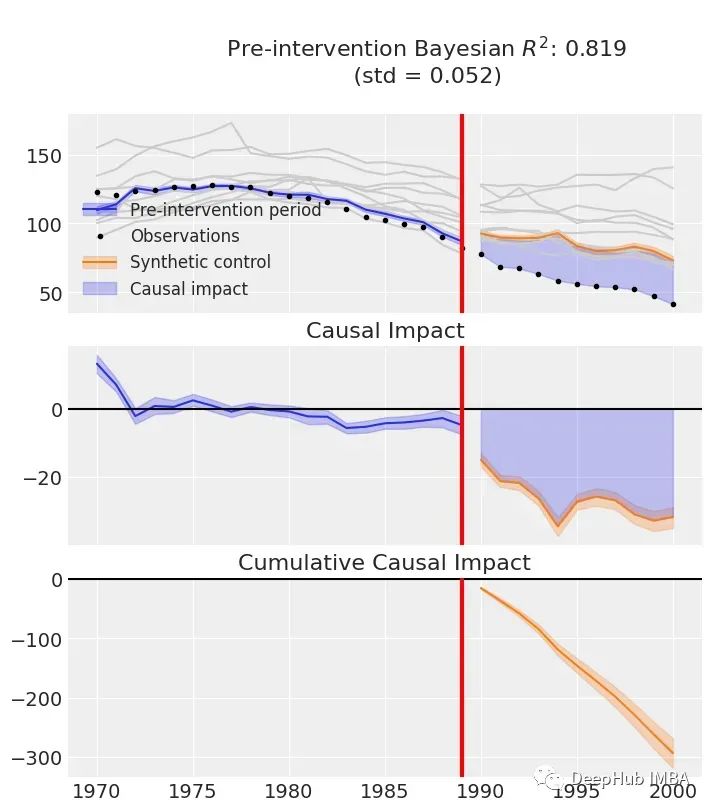
这是我们在拟合模型后得到的主要图形。首先要确保我们有一个好的模型,也就是说要构建一个好的合成组。上面的结果实现了~82%的R2,可以说效果还不错。CausalPy在第一个小图中用橙色显示了加州在没有干预的情况下的情况。黑点表示实际观测结果。另外两个子图显示了合成对照组和干预组之间的(累积)差异。最主要的石我们还得到了与因果效应相关的可信区间。
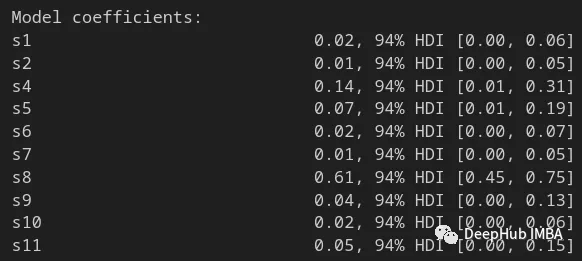
还可以查看WeightedSumFitter的系数。这再次表明合成的加州是其他州的组合。在这种情况下,s8和s4构成了合成加州的很大一部分。
总结
因果推理是一种推理过程,通过观察事件或现象之间的关系,推断出一个事件或现象是另一个事件或现象的结果或原因。它是从一个或多个前提中得出结论的过程,其中前提描述了可能的原因和结果之间的联系。
因果推理是统计学中一个经常被忽视的领域。它允许我们超越单纯的联想和相关性,并回答“假设”类型的问题。回答这些类型的问题对于实际做出基于数据的决策至关重要。
CausalPy 可以使用不同类型的模型用于准实验的因果推理,他的地址如下:
https://avoid.overfit.cn/post/8e3b56e584974ec3a1b3807c78095f76


