从roofline模型看CPU矩阵乘法优化

CPU上矩阵乘法优化被大家老生常谈，最早从goto的论文，到后来各种数学库的优化方法，以及很多工程师的优化经验总结。还能有什么新意呢？

本文用roofline模型来分析一下笔者n年前学习的矩阵乘法的优化方法。主要目的有两个，一是看笔者学习到的这种方法是否达到了最优？二使用roofline模型改进一下优化方法。

1. 背景知识

1.1. CPU的理论极限和算法的计算访存比

cpu理论极限计算方式=频率 * simd的向量寄存器容纳数据量 2 核数

cpu还有个重要的指标是它的从ddr上读取数据的带宽，处理器的性能是由这两者决定的，芯片设计者需要平衡两者的关系，根据处理器所需执行的大部分算法的特点来设计这两者。

算法的计算访存比描述了一个算法运行过程中需要多少访问存储量和计算量。当芯片的计算访存比和算法的计算访存比相匹配情况下，这种处理器就是最适合这种算法的处理器。然而实际的算法复杂度很高，以及处理器设计的通用性，这两者不相匹配时，就需要算法优化来使得计算或者访存的某一个方面达到处理器的瓶颈。此时算法达到了处理器可以执行的最好性能。

1.2. roofline模型

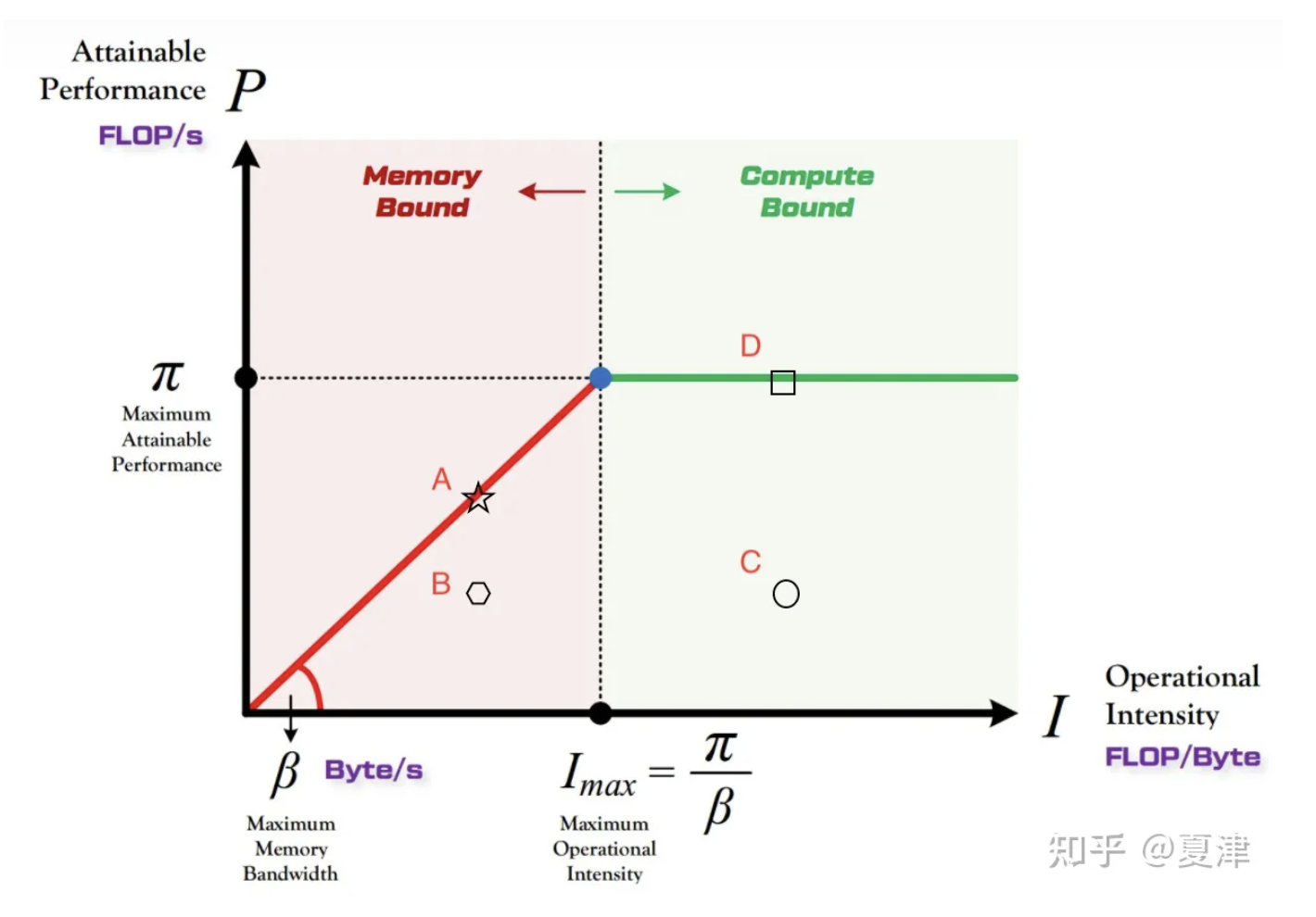
Roofline模型是由加州理工大学伯利克提出的，用来获得当前计算平台在不同的计算强度下能够达到的理论计算上限。进而获得程序的理论运行时间，为算法优化工程师提供优化方向指导。

例如有四种算法其分别落在图中的A、B、C、D四个点上，其中A和D点正好已经落在折线上，其性能已经达到最优，无法继续优化。而当算法落在B点时候，算法的计算访存比处于拐点的左侧，属于带宽瓶颈，但是程序并没有利用好处理器的带宽，优化方向应该往优化访存方向走。如提高数据的空间局部性和时间局部性。当算法处于C点时候，算法是计算瓶颈，但是没有完全发挥出硬件的计算性能。应该往计算优化方向走，如去除数据之间依赖、减少流水线气泡等。

图1

然而实际的算法和处理器是复杂的，如处理器的存储器结构是多级的，从寄存器到多级cache，到ddr上，其带宽不一样。算法上来说由于存在数据复用等行为，数据的访存量也不确定。我们可以分析具体问题，灵活运用roofline模型。

2. 在CPU上优化矩阵乘法

roofline模型为我们提供了一个分析程序理论性能极限的方法，并且提供了一个优化方向。优化之前，我们先介绍下处理器。我们使用的是ARM Cortex-A55核的NEON指令，一条向量乘加指令fmla指令的吞吐量是1，向量寄存器位宽是128bit，因此可以算出芯片对于半精度浮点数（16bit）的理论计算极限：

其从ddr到寄存器的带宽大概是4GB/s，因此计算访存比是6.4。

对于矩阵乘法，要读取两个矩阵A和B，生成一个矩阵C，若规模都是k k维度，则计算力为k k k 2，访存量为3 k k，那么计算访存比就为2/3k。可以看到其计算访存比不是常数。

实际上处理器的实际带宽还与cache的速率有关，cache的速率都会比ddr的带宽高。而且矩阵乘法的也不得不存在一些数据的复用和多次存储。所以很难确定其相对处理器是计算瓶颈还是带宽瓶颈。
我们可以通过控制变量法来让一个不确定瓶颈的程序达到最优性能。

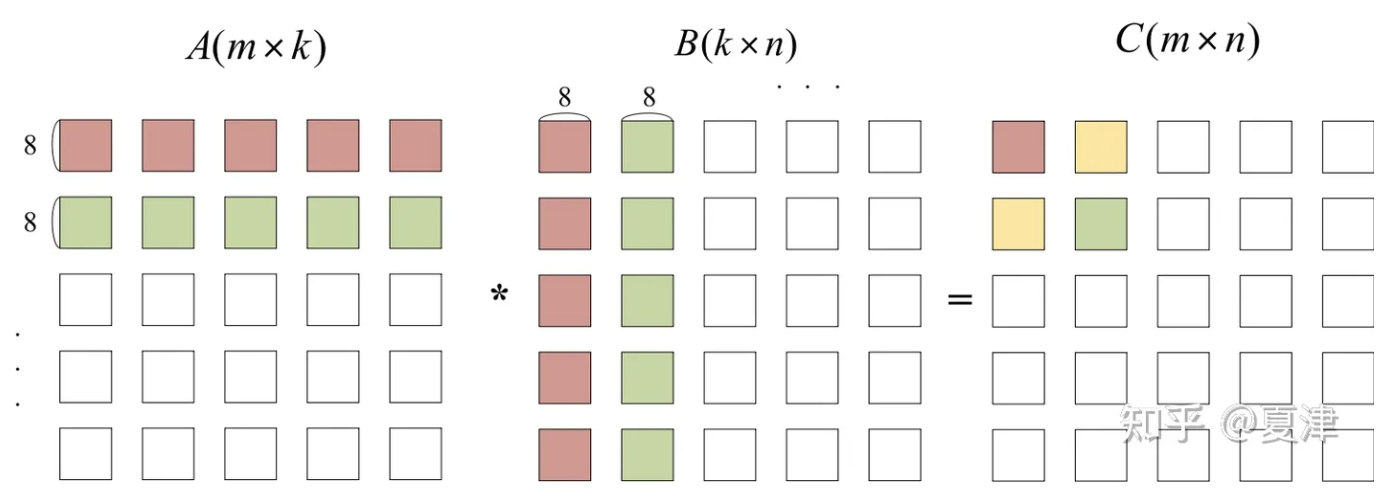
2.1. 步骤一：根据NEON指令的粒度，首先对矩阵进行第一次分块。

如下图所示。A的第一个（8xk）的长条矩阵，与B的第一个（kx8）的长条矩阵进行矩阵乘，生成C的一个（8x8）的小方块。依次类推，A的第一个小矩阵与B的第二个、第三个小矩阵进行相乘得到结果，直到B矩阵完全计算完再计算A的第二个小矩阵与所有B小矩阵相乘。

图3

那么我们如何确定小块内的NEON指令已经到达最优水平了呢？我们可以通过以下三个控制变量的步骤来确定。

（1）去除访存因素，获取最优NEON指令序列
roofline折线上表示的是程序可以获得的最大算力不会超过处理器的理论极限，这个理论极限是通过NEON指令集算出来的，我们去掉小块内访存相关的指令，让小计算块内的计算相关的指令流优化到理论水平。主要用到的方法是去除相邻的指令的读取数据的依赖等，让指令流达到理论的吞吐量。此时的指令流是最优的指令流，其计算访存比无限大，在roofline折线汇总可以达到图2中的D点的位置
（2）控制指令流不变，添加访存因素
现在我们在计算指令流中插入访存指令，由于现代处理器的多发射功能，如果访存指令访问的数据一直在cache中，那么插入的足够好的话，可以完全用计算的时间掩盖掉访存的时间，即时间不会增加。此时我们得到了一个最优的带有访存的指令流。
（3）控制之前的指令流不变，让数据读取地址连续增加
由于现代处理器有硬件预取功能，所以当访问一个大量的数据时候，连续的访问其地址可以达到最优秀的带宽，那么我们就让其数据一直连续进入即可。此时可以发现算法的计算访存比减少。获得的最大算力可能到达了拐点附近，甚至移动到了图2中的A点。

通过以上三个步骤，我们得到了一个最优的计算小矩阵块的指令流，通过在外层设置循环和数据重新排列，我们就可以得到一个可以执行通用矩阵乘法的算法。

这种写法可以充分的利用NEON指令，但是可以看下一个最小单元的计算访存比，

计算量：2x8x8xk
访存量近似为：2x2x8xk
计算访存比：4
计算访存比小于处理器的计算访存比6.4，可以知道其大致在roofline模型中的图二中的A点，我们可以在最优指令流的基础上进一步提高其计算访存比来提高性能，即往图2中的D点移动。

2.2. 步骤二：扩大计算规模，增加计算访存比

步骤一的使用NEON处理寄存器数目为10个，其中一个用来存储A矩阵的一小块，一个用于存储B矩阵的一小块，8个用于存储累加和C。根据ARM Cortex A55芯片的NEON个数是32个，以及提升计算访存比的需求，设计最小计算块大小为A矩阵（24xk），B矩阵为（kx8），矩阵C为（24x8）

计算量：2x24x8xk
访存量近似为：2x4x8xk
计算访存比：6
此时计算访存比和处理器的计算访存比6.4类似，更优。

2.3. 步骤三：访存优化，增加计算访存比

前面步骤一中我们提到了通过在外层设置循环和数据重新排列来完成整个矩阵乘法，设置数据重新排列的目的是让输入给最优指令流计算块的数据可以连续，以获取最优性能。
如果不进行数据重排操作，则存在一些跳读内存的情况，例如A矩阵和B矩阵都是行主序，则读取数据则必定会跳读内存，就需要重新从ddr中读取数据，这种方法会无法充分运用cache的带宽优势。

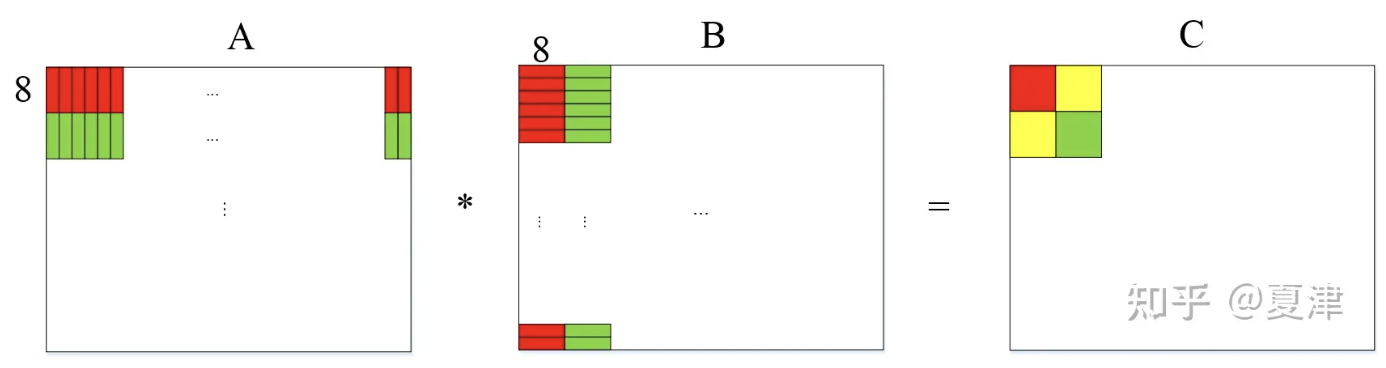
因此我们需要提前进行数据重排，让B矩阵的每一行的8列数据连续存储，A矩阵的每8行的同一列数据连续存储（或者24行）。这样可以保证输入给小计算块的数据是连续的，如图4所示。

图4

当然访存优化还有一个考虑因素是cache的规模，需要保证A矩阵的小块，B矩阵的小块以及C矩阵加一起小于cache的规模，这样可以首先让A的小块保持在cache中，轮流计算B矩阵的所有小块。

3. 总结

结合roofline模型和矩阵乘法优化方法。可以认为，在步骤一，目的是确保我们的最小计算部分的指令流可以一直在roofline折线上移动，步骤二和步骤三是在步骤一基础上，将计算访存比提高，使得点在折线上尽量往右移动。通过这三个优化我们就可以获取理论上的最优计算性能。折线上不能有其他点高于此种优化方法。

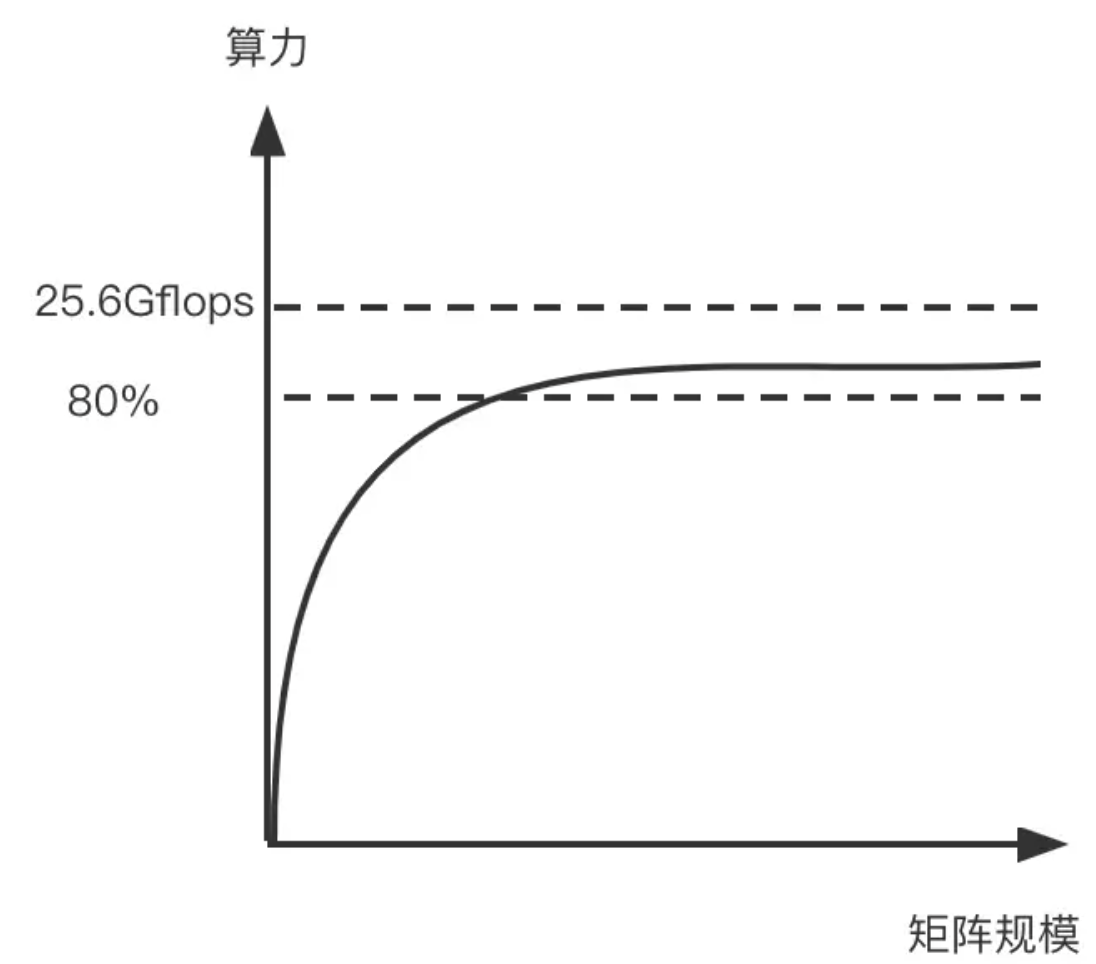
最后得到的性能数据如下图所示，可以看到随着矩阵规模的变大，获得的性能逐渐上升（由于计算访存比的上升），一般情况下可以达到理论极限的80%以上。

图5

作者：夏津
文章来源：知乎专栏

推荐阅读

更多嵌入式AI干货请关注嵌入式AI专栏。欢迎添加极术小姐姐微信（id:aijishu20)加入技术交流群，请备注研究方向。