本文将深入研究嵌入、矢量数据库和各种距离度量的概念,并提供示例和演示代码。
NLP中的嵌入
嵌入是连续向量空间中对象、单词或实体的数值表示。在NLP中,词嵌入捕获词之间的语义关系,使算法能够更好地理解文本的上下文和含义。
让我们试着用一个例子和一些可视化的方法来理解它:假设有6个句子,想要创建嵌入
from sentence_transformers import SentenceTransformer
# Sample text embedding model
model = SentenceTransformer('paraphrase-MiniLM-L6-v2')
#Sentences we want to encode. Example:
sentence = ['The team enjoyed the hike through the meadow',
'The team enjoyed the hike through the mountains',
'The team has not enjoyed the hike through the meadows',
'The national park had great views',
'There were lot of rare animals in national park',
'Olive oil drizzled over pizza tastes delicious']
#Sentences are encoded by calling model.encode()
embedding = model.encode(sentence)
#Preview the embeddings
print(embedding)
# As we can see embeddings are nothing but
# numerical representation of sentences in a vector form
[[ 0.37061948 0.26414198 0.21265635 ... 0.14994518 -0.25794953
-0.23970771]
[-0.07645706 0.27122658 -0.04530133 ... -0.27319074 -0.60025024
-0.302555 ]
[ 0.35693657 -0.2331443 0.418002 ... -0.37369558 -0.10241977
-0.03282997]
[ 0.66933334 0.40094966 -0.48208416 ... 0.10645878 -1.5067163
-0.01547382]
[ 0.4339616 0.2323563 0.21751338 ... -0.5746389 -0.26438454
0.492655 ]
[-0.2655593 0.11172348 -0.1473308 ... 0.42197517 0.88394576
0.10763898]]可以看到我们获得了一个384维度的嵌入
embedding.shape
(6, 384)然后我们使用PCA进行降维并使用matplot可视化
from sklearn.decomposition import PCA
# Perform PCA for 2D visualization
PCA_model = PCA(n_components = 2)
PCA_model.fit(embedding)
new_embeddings = PCA_model.transform(embedding)
# As we can see now the shape has changed from (6,384)->(6,2)
Shape: (6, 2)
[[-2.7454064 -1.628386 ]
[-2.7024133 -2.0113547 ]
[-2.6084075 -2.5289955 ]
[ 0.62488586 3.9073005 ]
[ 0.09110744 4.9031897 ]
[ 7.3402357 -2.6417546 ]]PCA将其维度降维2 这样可以显示在2D的散点图上
import matplotlib.pyplot as plt
import mplcursors
def plot2d(x_values, y_values, text_labels):
"""
Create a 2D plot with annotations.
Parameters:
- x_values (array): X-axis values.
- y_values (array): Y-axis values.
- text_labels (list): List of text labels for each point.
"""
fig, ax = plt.subplots()
scatter = ax.scatter(x_values, y_values, label='Data Points')
# Annotate points with text labels
for i, label in enumerate(text_labels):
ax.annotate(label, (x_values[i], y_values[i]))
mplcursors.cursor(hover=True)
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_title('2D Plot with Annotations')
plt.show()调用这个函数,结果如下
import matplotlib.pyplot as plt
import mplcursors
# pass the embeddings and original sentence to create labels
plot2d(new_embeddings[:,0], new_embeddings[:,1], sentence)
现在你可以看到,彼此相似的句子被投影到彼此附近,这实际很有意义。例如,提到“National Park”的句子彼此靠得更近,谈论“hiking”的句子彼此靠得更近。
如何度量这些句子嵌入之间的距离?
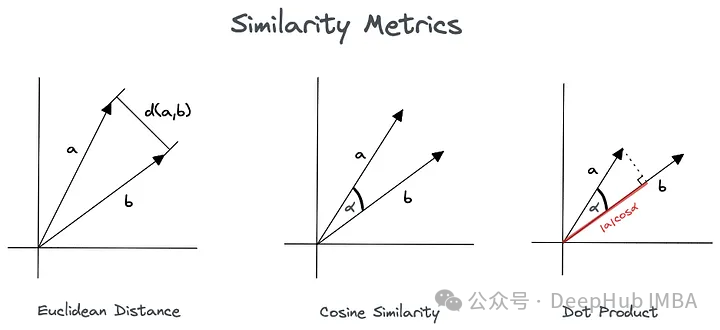
有很多方法可以计算两个向量之间的距离,我们将介绍矢量数据库中常用的4种距离度量
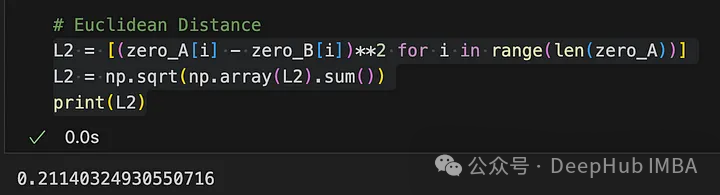
1、欧氏距离
两个向量之间最短路径的长度

欧几里得距离很容易理解,因为它测量空间中两点之间的直线距离。它适用于矢量元素之间的大小和绝对差异很重要的情况。
但是欧氏距离对数据的尺度很敏感。如果特征具有不同的尺度,则距离计算可能被尺度较大的特征所主导。并且在高维空间中,欧几里得距离可能变得不那么有意义,因为由于“维度诅咒”,距离趋于收敛。
考虑二维空间中的两点:A(1,2)和B (4,6), A和B之间的欧氏距离计算为:
2、余弦距离
测量矢量之间的方向性差异
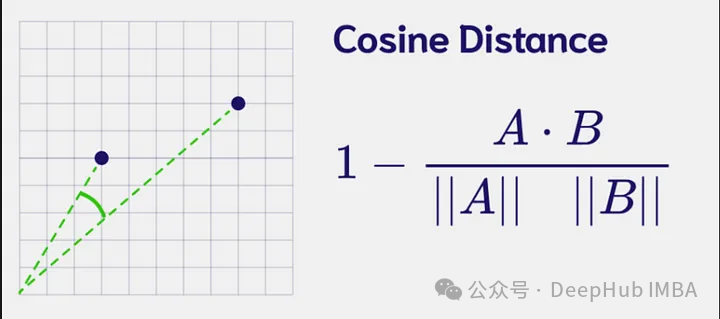
余弦距离不受向量大小的影响,使其对尺度差异具有鲁棒性,非常适合高维空间。
余弦距离只考虑向量的方向,而不是它们的大小。如果两个矢量方向相似,但长度相差很大,那么它们的余弦相似度可能接近于0。

3、Jaccard
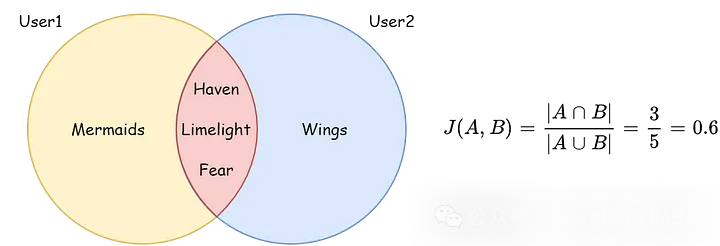
Jaccard系数度量有限样本集之间的相似性,定义为交集的大小除以样本集并集的大小:

在处理集合或二元数据时,Jaccard特别有用,使其适用于文本文档比较等场景。像余弦相似度一样,Jaccard对大小不敏感。
但是它主要是为二元数据设计的,它可能不适合连续数据或大小信息至关重要的情况。当两个集合都为空时,Jaccard相似度是未定义的。
4、曼哈顿距离

曼哈顿距离,也称为L1距离或出租车距离,它测量基于网格的系统中两点之间的距离,只考虑水平和垂直运动。
曼哈顿距离直观且易于解释。它对应于出租车在网格状道路系统上行驶的距离,在水平和垂直方向上行驶以到达目的地。这种简单性使得它在可解释性至关重要的场景中特别有用。
曼哈顿距离在处理以表格形式表示的基于网格的系统或数据集时非常适用。它非常适合沿网格线移动的场景,例如在物流、运输和图像处理中。
但是曼哈顿距离的一个重大缺点是它对数据规模的敏感性。如果特征具有不同的尺度,则距离计算可能被尺度较大的特征所主导。在处理特征大小不同的数据集时,这可能导致次优结果。
并且曼哈顿距离本质上受限于沿水平和垂直轴的网格运动。在特征之间的对角线移动或非线性关系至关重要的情况下,曼哈顿距离可能无法准确捕获数据中的潜在模式。
余弦相似度vs正弦相似度
还有一个更有趣的问题是为什么我们用余弦而不是正弦相似度来测量矢量距离。
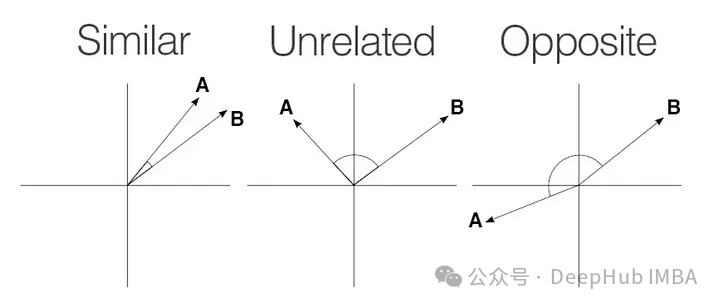
余弦相似度比正弦相似度更常用于测量向量之间的相似度。余弦和正弦相似度之间的选择取决于数据的性质和任务的具体要求。让我们来探讨一下为什么余弦相似度是首选:
余弦相似度度量的是矢量之间的夹角余弦值,而正弦相似度度量的是夹角的正弦值。余弦相似度更直接地表示矢量指向的相似度,而正弦相似度则在一些情况下可能不如余弦相似度直观。
余弦相似度的计算中包含了矢量的内积,而正弦相似度则涉及到矢量的外积。在高维空间中,矢量之间的内积更容易计算,而外积可能涉及到复杂的计算。因此余弦相似度的计算在实际应用中更为高效。
余弦相似度与向量之间的角度直接相关。余弦相似度为1表示向量指向相同的方向,而相似度为-1表示它们指向相反的方向。相似度为0表示正交性。这种直观的解释与许多应用程序非常吻合。
正弦相似度在实践中不太常见是它测量向量间夹角的正弦值,强调相似度的垂直分量。虽然正弦相似度可能有特定的用例,例如垂直度至关重要的场景,但余弦相似度由于其在规范化、定向解释和效率方面的优势而被更广泛地采用。
总结
本文探讨了嵌入和距离度量的概念,理解和利用这些概念对于在各个领域构建高级NLP模型和应用程序至关重要。因为在实际应用中需要考虑尝试不同的模型、数据库和指标,并针对特定用例进行优化性能。
https://avoid.overfit.cn/post/8c9ee01acff64699bdc8a194c0e1247b


