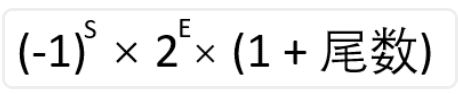IEEE 754 Floating NaN在深度学习计算中的行为

计算机对浮点数的表示都是对真实实数的近似，计算机系统必须小心计算机算术和真实世界算术的差距，程序员也务必小心近似值的含义。

计算机用于模拟近似真实世界的位模式，并没有内在的含义，它们代表的可能是有符号整数、无符号整数、浮点数、指令、字符串等，具体代表什么取决于对其操作的指令。

1.浮点表示

标准的存在使几乎每台计算机都遵循，简化浮点程序接口且提高运算质量，也是软硬件的接口。

浮点相较于定点，在字面意思上来说，float表示binary point是浮动的，而且定点的计算机二进制表示是基于固定的位模式，Fixed，定点每个二进制表示都是特定值，一个萝卜一个坑，因而没有Inf和NaN。浮点符号位（S）、尾数位（F）和指数位（E）打来的表示位宽的实数区间大。

如为了打包更多数据位，标准隐藏了规格化（规格化：用没有前导零的浮点记数法表示数；前导零：小数点左边的整数部分为0）二进制数小数点前面的1。

尾数表示一个0~1之间的数，E指明了指数字段的值，若从左到右将尾数各位标记位s1,s2,s3,…，则数的值为：

(-1)^S × [1 + s1×2^(-1) + s2×2^(-2) + s3×2^(-3) + …]×2^E

因此，数据有效位：

在单精度下，数据有24位（隐含的1和23位尾数）
双精度则是53位（1+52）

为了精确，用术语有效位（significand）表示24位或53位的数，即隐含的1加上尾数。特别说明一下0这个数值如下图，0没有前导1，指数保留为0，所以硬件不会将1加到尾数前面。那自然这样的表示法，因符号位的0或1取值让其具有正负。0是个例外，其他数表示不变。

特别说明，符号位在最左边的最高有效位上，是为了便于比较排序，相比整数定点数的分类，浮点稍微复杂，标准的这种记数法本质是符号与幅值的形式，而非补码。

有符号整数的二进制表示

既然说到这两个关键词（补码、符号与幅值），那回顾下有符号数的表示。

符号与幅值的表示法即字面意思，作为早期提出用来表示区分定点数表示中正负数的一种方法，其缺点如符号位的位置在左还是右、计算需要额外引入符号的设置步骤、单独的符号会给0值的表达带来正负性。而且还有个问题是，当用一个较小数减去较大数时如 21-42，会有借位行为，无符号的表示会让较小数前面的 0 中借位，导致前面的位变成一连串的 1 。

在没有其他更好的方案下，有符号二进制表示最终解决方案取决于硬件易于实现的方法（二进制补码）：

前导位为 0 表示正数， 1 表示负数
求某负数的补码，可以先将其看成正数然后对二进制形式各位取反后加1
如计算 21-42的计算过程，原本的减法视为加法，即正 21 与负 42 相加。先将两个数以二进制表示
- 21： 0b00010101
- -42：先当作正数42表示为 0b00101010，然后按照上面讲的各位取反得 0b11010101，再加1得 0b11010110
- 剩下的计算就是两个二进制表示计算即可，得 0b11101011，符号为是1肯定是负数，即-21
拿有符号8位举例说，其二进制的表示从正数 0b00000000（即20-1，0）到 0b01111111，即（27-1，127），后面是按绝对值递减的负数，从绝对值最大的负数 0b10000000（即-27，-128）到 0b11111111（即-1）
补码优点在于负数最高有效位都是1，硬件只需要检测这一位数就能判断正负，该位也称为符号位

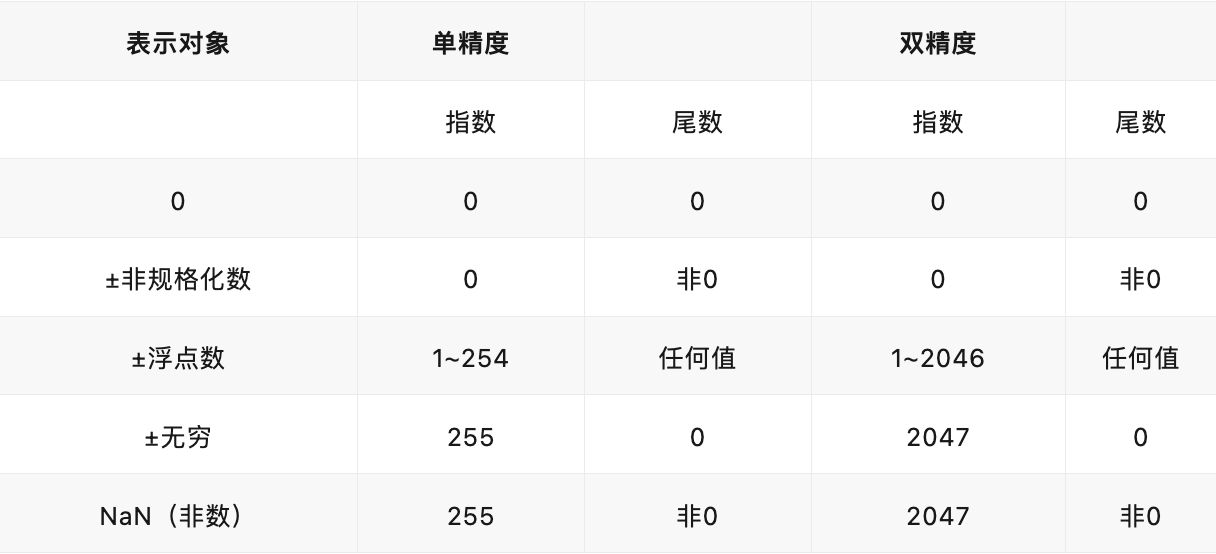
上面这一段都是讲的有符号定点，再回到浮点数的表示，下面表格给出IEEE 754在单精度和双精度浮点数上的编码表示。

表中想表达的信息：

用特殊的符号来表示异常事件，如软件上可以设置结果设置为某种格式表达正负无穷、非数，代替除0中断；
指数被保留下来，用以标识特殊符号，即正负无穷，非数的表示上。
- 从字面意思来说，非数不是一个数，这是标准为了表示无效操作而不得不引入的，如 0/0或无穷减无穷。目的也是为了让计算无效的这一个结果得以保留，让程序员知道这里这个操作是无效的，可以在程序后续的过程中在做决断，或者在测试中使用发现一些特殊的情况。
- 无穷，其存在目的是形成一个拓扑闭包。这句话对于非数学专业的同学很难理解，粗略的比喻是：想象一个装满小球的开放盒子，小球表示实数轴上的有限数（不要细究这个“有限”的意思），把盒子“封闭”意味着不让任何小球从盒子里掉出来，但盒子顶部是开放的，没有盖子，为此需要加一个盖子，这个盖子就代表了“无穷大”。拓扑学中，“闭包”是一个包含了原集合的所有极限点的集合。在我们的比喻中，这些极限点就像是试图从盒子边缘逃出的小球，但由于加上了盖子（无穷大），它们都被包含在了闭包（封闭的盒子）之内。无穷大的概念确保了空间的“完整性”，使我们在这个空间内进行连续的数学运算而不会出现“漏洞”或“不连续”。
非规格化数：规格化我们知道是用没有前导零的，进一步说：
- 在规格化的表示总假设有一个无需存储的尾数位最高位1，即在小数点前，从而节省空间提高精度；
- 指数部分不全位0或1，留给特殊值如零、无穷和非数。

如二进制浮点数3.1415927，在本文开始的图示中有表示其尾数位为1.5707964×2^1。而非规格化（denormalized）或称为亚规格化（sub normalized）是为了进一步最大限度获取精度位，也是标准允许的，减小 0 和最小规格化数的间隙，非规格化数和 0 有相同的指数，但尾数非 0 ，非规格化允许有效位变小直到位 0 ，称为逐级下溢（gradual underflow），如正的单精度规格化数是1.00000000000000000000000two×2^(-126)，two是以2为基数，

而最小单精度非规格化数是：0.00000000000000000000001two×2^(-126)，即1.0two×2-149，这种非规格化带来的麻烦，是对浮点单元的硬件设计角度而言。因此，许多计算机在操作数出现非规格化数时会产生异常，较给软件来完成相应操作，虽然软件可以处理但是低效。

2.NaN

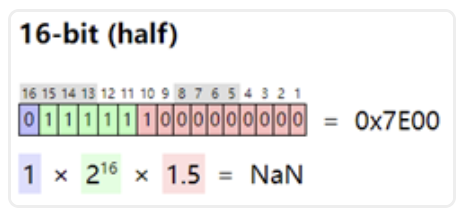
非数由754-1985引入，其二进制表示为：指数位全1，尾数位非全0，对于半精度亦是如此。

下图是FP16的NaN二进制表示，符号位、指数位和尾数位分别用蓝色、绿色和红色表示，这里重点关注其数值，FP32和FP64类似。

2.1 与NaN的操作

说操作前，先说下标准中定义的NaN有两类：

静默（Quiet）：qNaN，默认的异常处理行为，NaN被保留下来，不会产生异常或中断，该特殊值可以被传播下去；
信号（Signaling）：sNaN，即发信号的。产生的同时会发出无效操作异常。

下面关于静默和非静默分别举一些例子，与标准可能存在不同。

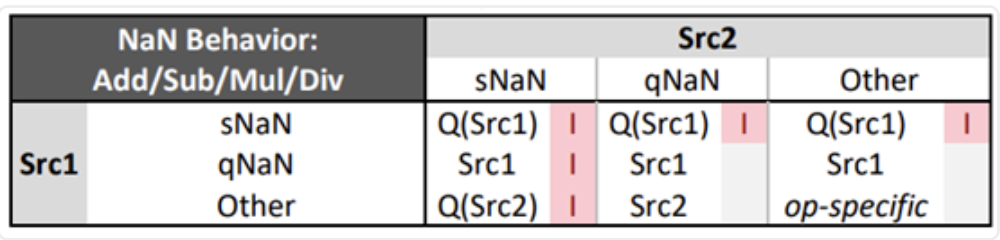
第一个例子，Intel架构对浮点行为有一个表格用来说明，下面加减乘除在SSE、AVX Scalar指令的行为，其中，Src1和Src2分别表示两个操作数：

可以看到只要两个操作数有sNaN的结果都是Invalid，而只有qNaN时qNaN被保留。

第二个例子，在某些硬件平台上，对同一个功能的指令会有不同的版本：静默和信号，当指令遇到某些值时会发出异常，而静默版本的不会。

第三个例子，OpenCL中有符号常量来表示无穷和静默非数（能表示的肯定是静默的），在单精度浮点的精度下表示为：

OpenCL规范在对754标准上的遵循，有专门的说明，参考：https://registry.khronos.org/OpenCL/specs/3.0-unified/html/OpenCL_C.html#opencl-numerical-compliance。

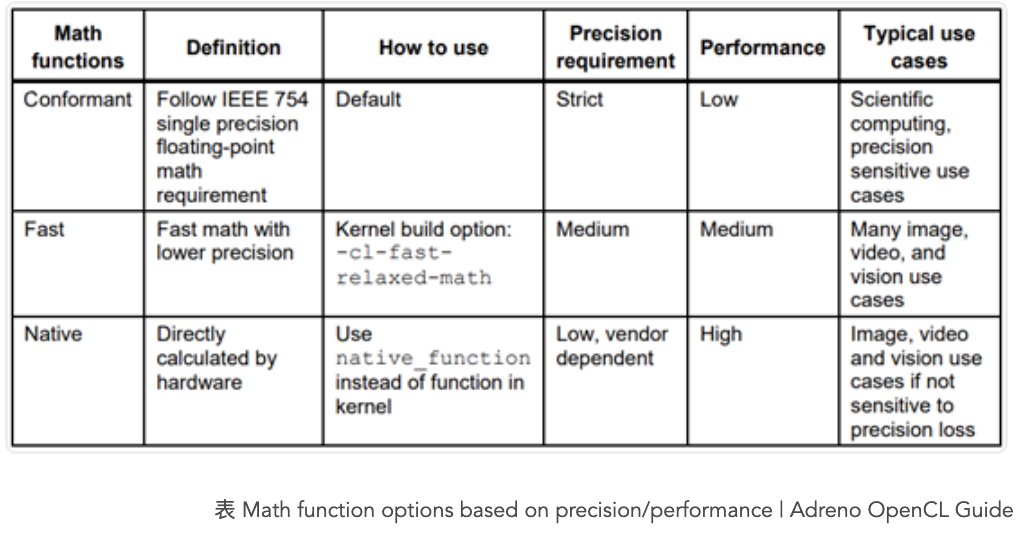
再补充一点，OpenCL对边界场景的行为分为两类：遵循C99规范以及特别的。对Adreno GPU来说，遵循规则意味着一种平衡，下表是Adreno GPU OpenCL文档，可以看到性能方面为了支持754标准带来的折损：

讲到这里，不得不扯远一点，754标准与性能的关系。

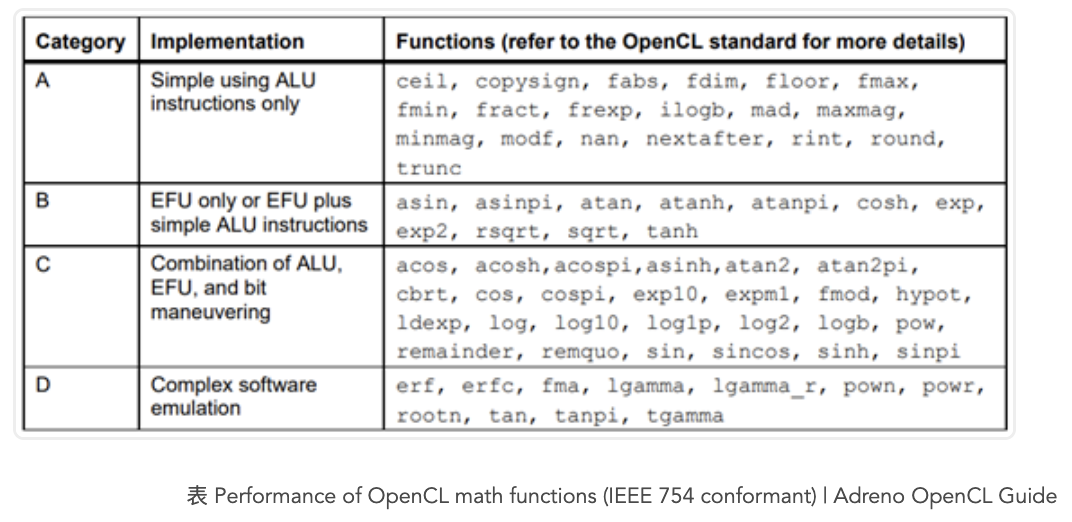
Adreno GPU有一个用于加速基本数学运算的硬件模块，称为基本函数单元（EFU，Elementary function unit），基于ALU性能最优，然后是EFU计算的函数，其次是通过EFU和ALU运算结合起来计算的函数，性能最不好的自然是编译器使用复杂算法仿真出来的。下表是Adreno GPU OpenCL函数列表，性能最好的是A类函数。

除了NaN的两个类型外，下面再介绍一些摘自754标准有关NaN的操作：

一个或多个NaN输入的操作结果是静默NaN。如前文Intel架构浮点数的加减乘除符合该规则
输入有NaN的操作，预期结果是浮点类型的话，那应是NaN
其中，逐元素的maximum和minimum例外，当NaN和非NaN作为操作数时，结果会返回另一个非NaN的数。但有时候你却希望保留NaN，像ARMv8就提供两种max/min：保留NaN和不保留的，见下图。

图浮点Min/Max | ARMv8指令集概览

NaN传递过程中，尾数位不会被改变，但格式转换不保证
为了处理可能包含NaN的比较，754标准包含了有序（ordered）和无序（unordered）比较。如ARMv8指令集有很多种用于比较的指令来支持出现NaN的情况，这点我想是和后文要说的 TotalOrder 有关的。

2.2 NaN的二进制编码

正如刚开始介绍的，对于编码是符号位不限制，且尾数位只要非0即可，这种灵活便携性，让NaN有不固定的二进制编码：

qNaN：尾数位第一个必须是1
sNaN：尾数位第一个必须是0，其它尾数位必有一个1（这点是区分Inf）为了更形象地表示，下面从上到下依次为qNaN、sNaN和Inf。

因为NaN的编码不唯一，自然引出“有效载荷”（Payload）这个概念，表示尾数位置除了最高的两位（通常区分qNaN和sNaN）外的其余位，如double的尾数位有52个，排除前面2位，有效载荷就是50。

再说符号位：

当输入或结果是NaN时，该标准不解释符号位的含义：
但在标准提到 TotalOrder(x,y)这么个谓词函数，用于定义特定格式的全序关系，两个数比较必然是三个关系其中之一（小于、等于、大于），这对于浮点数处理尤其存在特殊值（Inf和NaN）时很有用处，totalOrder可以正确处理带有特殊值的情况，标准定义了存在NaN时该函数的返回关系，具体参考标准章节 5.10Detailsof totalOrder predicate，本文不展开
对TotalOrder外的其他操作，标准不指定NaN结果的符号位
对位串的操作（copy、negate即取反、abs、copySign即两个操作数把一个操作数的符号给到另一个数上并返回），这些操作的符号位是确定的。

2.3 NaN传播与转换规则

还是摘自标准的内容，想不出一个例子直接看还是有些乏味晦涩：

有效载荷（Payload）
- 当且一个NaN输入输出NaN时，有效载荷不应被改变（当目标格式支持的情况下）。比方输入是FP64的NaN了，输出也是FP64的NaN，那么有效载荷也就是尾数位不要被这个计算修改。这个要求是对运算实现的要求，即NaN的传递；
- 当多个NaN输入输出一个NaN时，输出NaN有效载荷应同输入的其中一个。这个也可以理解，比方你两个输入分别是FP32和FP16的NaN，输出是FP16 NaN，那么输出和输入的FP16的NaN一样，或者类型都一样的时候，和其中一个一样。
转换一致性
- NaN从一较窄格式转换到较宽格式（同基数下），再转换回较窄格式，除规范化外，不应该更改有效载荷。比方FP16的NaN转到FP32的，再转回FP16的NaN。这点有点费解，因为FP32的有效载荷肯定比FP16的多，从窄到宽再回到窄的过程中，从宽回到窄肯定会丢精度。这个标准这条有点看不懂，我的理解是FP16 NaN的表示只有一种位模式，那么是可以符合的。
无法保留有效载荷时的转换规则（灵活性）
- 这种场景是不允许保留有效载荷相同或不同基数的浮点格式时，应返回一个提供诊断信息的NaN，藉由有效载荷提供。如从宽的FP32的NaN转换到窄的FP16，这个过程有效载荷不同无法完整保留原有类型的有效载荷，那么结果NaN的有效载荷应该提供这样的信息。

3.应用行为：NaN计算

当运算中存在NaN和非NaN的比较时，深度学习框架的行为是关注的重点。后面的内容都以激活函数ReLU为例，这个太特别了，因为其实现是通过elementwise maximum实现，关键是754标准对逐个元素比较大小的行为，当存在NaN的时候是这么定义的：

For an operation with quiet NaN inputs, other than maximum and minimum operations, if a floating-point result is to be delivered the result shall be a quiet NaN which should be one of the input NaNs.

即当有NaN和非NaN时，返回另一个非NaN的数。这个规范为什么这么定义，我想，NaN是一个非数和另一个不是非数的数比较：

*   那么取大或者取小返回数肯定比非数合理吧？这么说似乎也有道理；

*   但是你说不合理，也不合理，因为这个操作是比较，突出的是两个数的比较关系，如果两个操作数不合理，那么这个比较操作就是无效的，那么比较的结果自然没有意义。

我个人的倾向是比较操作是无意义的，没有想到哪些具体的场景需要返回另一个非NaN的数。

下面来看下在深度学习框架、Python、Adreno OpenCL上对NaN的行为。

PyTorch与TensorFlow

后续在PyTorch和TensorFlow上也分别做了实验，输入是NaN时，结果对NaN保留下来：

# PyTorch

a=torch.
Tensor
(range(-
3
,
3
))

a[-
1
]=np.nan

torch.nn.
ReLU
()(a)  
# 输出结果：[0,0,0,0,1,nan]

# TensorFlow

Tf
.keras.layers.
ReLU
()([np.nan])  
# 输出结果 [np.nan]

Python

Python对NaN的计算分为两类，这两类也不限于Python：

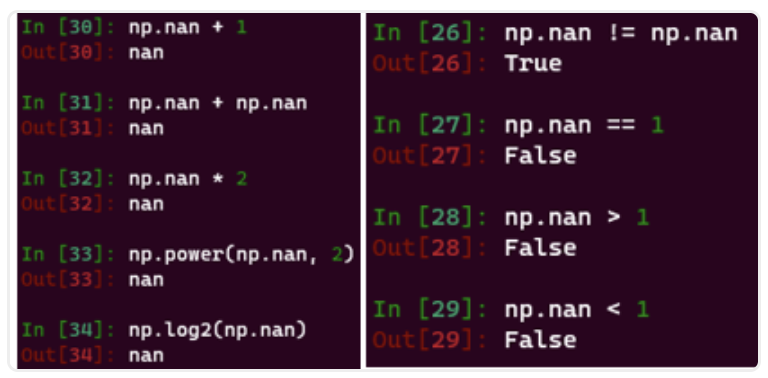
关系运算：NaN与任何数比较关系，都返回False；除了特例：NaN!=NaN的比较返回True；
算术运算：NaN与任何数的计算都是NaN，即被保留。特例见下面有关754标准和max/min接口。

此外，Python提供至少三种逐元素的大小比较：

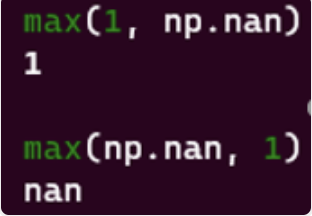
max/min: max(np.nan,1)返回1，max(1,np.nan)返回np.nan，行为不好描述，文档更没有提，见上图；
np.maximum/np.minimum：np.maximum(1, np.nan)返回np.nan结果稳定，NaN会被保留下来，符合TF和Torch的行为；
np.fmax/np.fmin: np.fmax(1, np.nan)返回另一个非nan的数即1，传递NaN这点看起来是遵循754对NaN的计算要求的，但不符合我们实际的需求（需要与主流深度学习框架保持一致）。

OpenCL

这里没有说max(x, NaN)返回什么，我也没有在某个硬件上实验。但有一些猜想：

返回什么取决于x和y的参数顺序，因为文档里说是returns y if x < y，如果x和y里有一个NaN那么关系比较运算是False，返回y，那就看y是NaN还是x是NaN了;
返回NaN。我个人认为应该遵循C99的规范，因为一来是fmax这个接口用来遵循754就可以了，另外是x和y的比较运算因里面有一个NaN结果应该是False，那么返回的是NaN。而且在stackoverflow上有检索，在C/C++上的大小比较max和fmax，fmax遵循754标准返回另一个数，而max返回NaN。

如果并非如此，就需要实现一个传递NaN的OpenCL max实现，可以通过OpenCL提供的函数如nan(...)和isnan(...)来实现，结合select(…)等方法可以带上mask。但需注意的是同一个接口在标量和矢量操作数时，是否返回一样的类型或值，如比较关系结果是True那么可能标量接口返回的是和向量接口类型不一样的值，这点需要注意。