在追求高效代码的路上,我们不可避免地会遇到代码的性能瓶颈。为了了解、解释一段代码为什么低效,并尝试改进低效的代码,我们总是要了解硬件的工作原理。于是,我们可能会尝试搜索有关某个架构的介绍、一些优化指南或者阅读一些计算机科学的教科书(如:计算机组成原理)。但以上的内容可能都太过繁琐、细节太多,在阅读的过程中,我们可能会迷失在纷繁的细节中,没法很好地将知识运用到实践中。
本文旨在通过多个可运行的 benchmark 介绍常见的优化细节以及与之相关的硬件知识,为读者建立一个简单、有效的硬件心智模型。
Cache
首先要介绍的就是缓存 cache 。我们先来看一个引自 CSAPP 的经典例子:
pub fn row_major_traversal(arr: &mut Vec<Vec<usize>>) {
let n = arr.len();
for i in 0..n {
assert!(arr[i].len() == n);
for j in 0..n {
arr[i][j] += j;
}
}
}
pub fn column_major_traversal(arr: &mut Vec<Vec<usize>>) {
let n = arr.len();
for i in 0..n {
assert!(arr[i].len() == n);
for j in 0..n {
arr[j][i] += j;
}
}
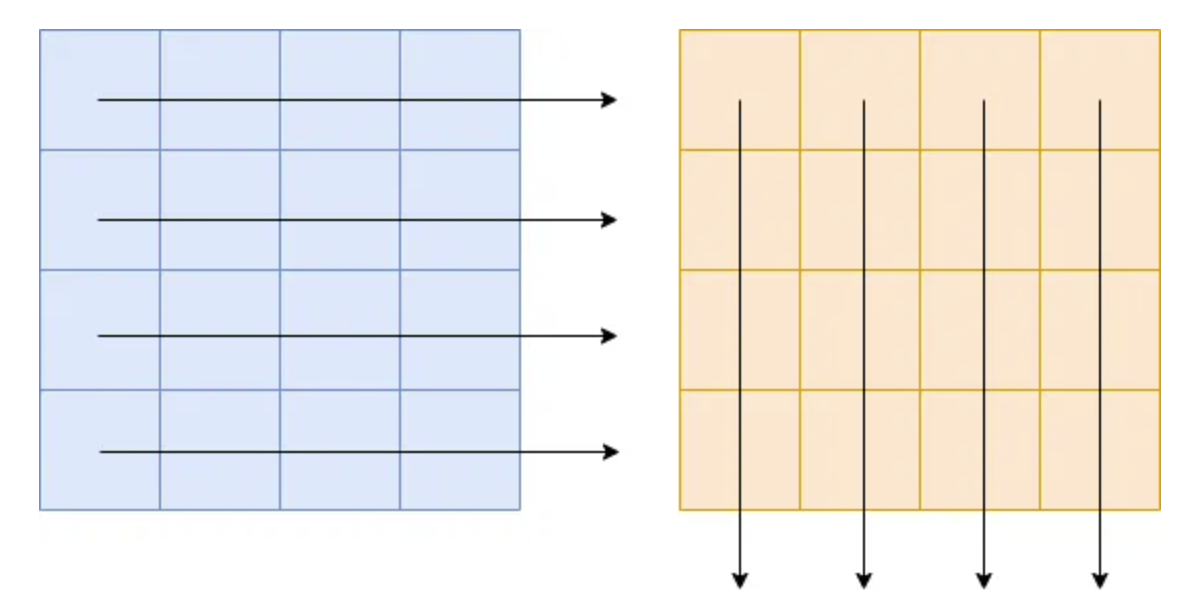
}在上面两个例子中,分别按行、按列迭代同样大小的二维数组。
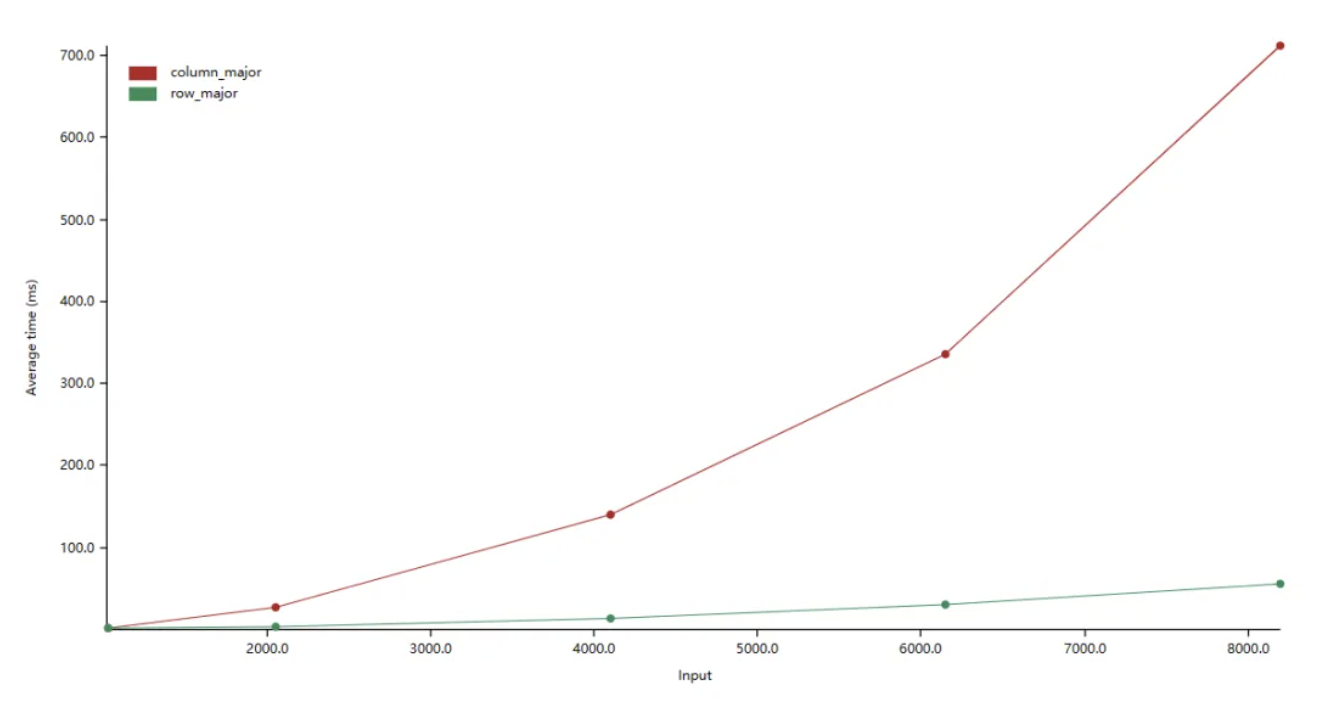
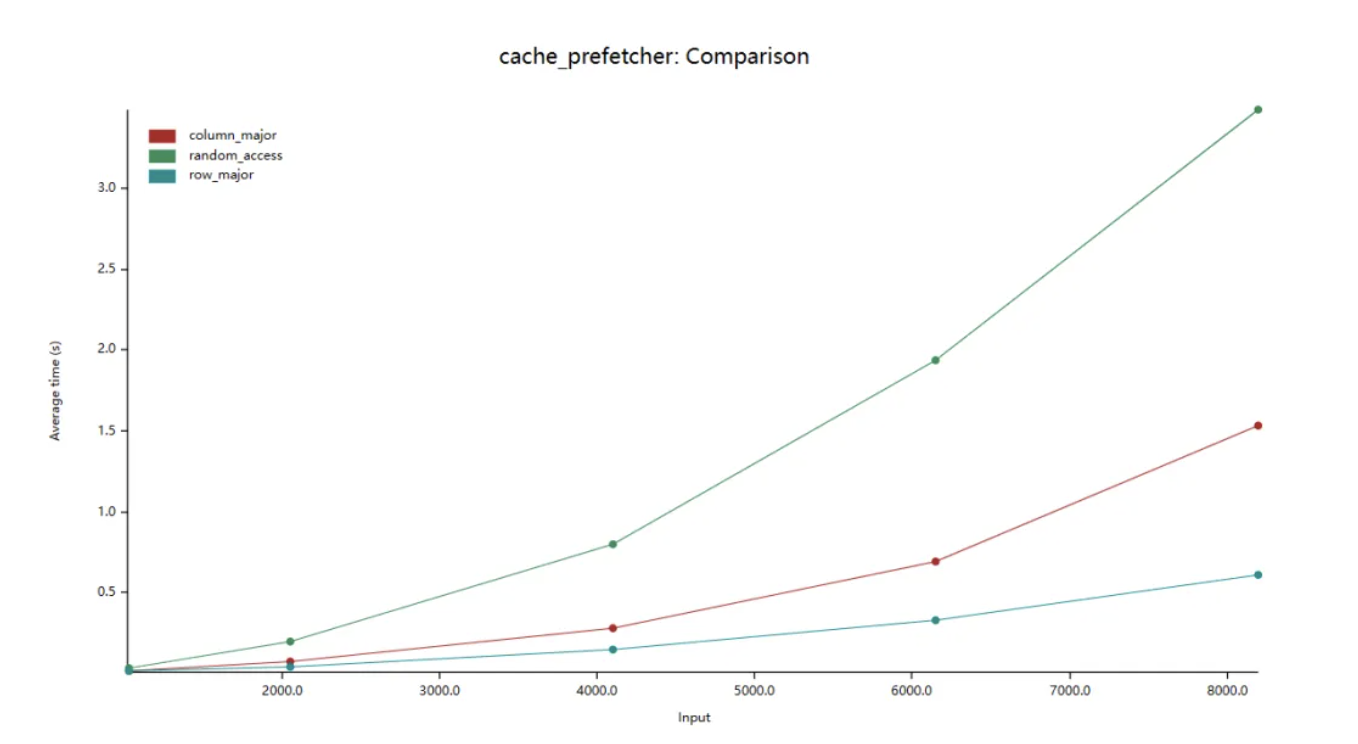
我们对这两个函数进行 benchmark:
在上图中,纵轴是平均耗时,横轴是数组大小(如:2000.0 表示数组大小为:2000 x 2000)。我们看到按行迭代数组比按列迭代的效率高约 10 倍。
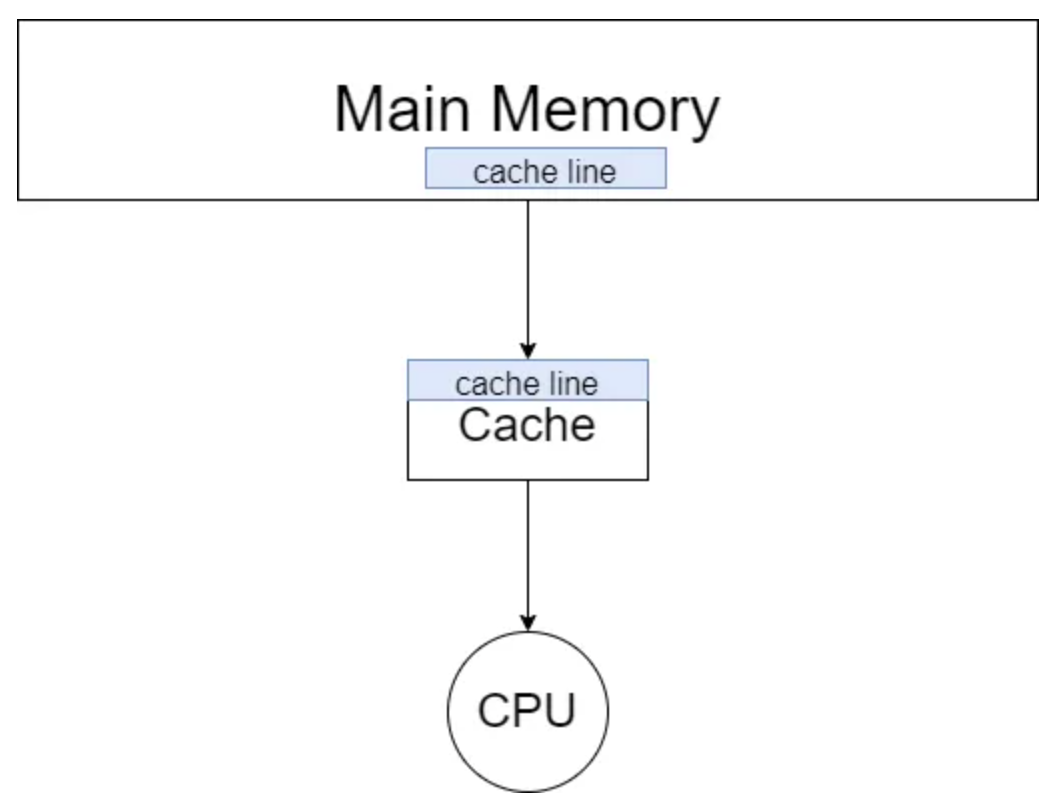
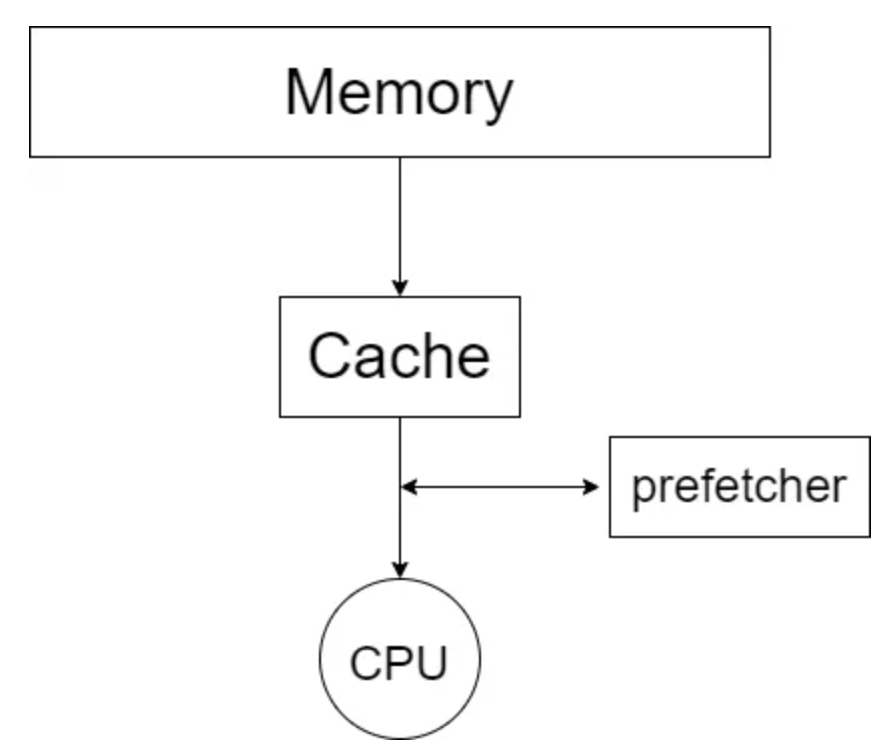
在现代的存储架构中,cpu 和主存之间是 cache 。cpu 中的寄存器、高速缓存、内存三者的数据读写速度越来越慢。
而当 cpu 读取一个数据的时候,会先尝试从 cache 中读取。如果发生 cache miss 的时候,才会将数据从主存中加载到 cache 中再读取。而值得注意的是,cpu 每一次的读取都是以 cache line 为单位的。也就是说,cpu 在读取一个数据的时候,也会将该数据相邻的、一个 cache line 内的数据也加载到 cache 中。而二维数组在内存中是按行排布的,换句话说,数组中相邻的两行是首尾相连排列的。所以在读取 arr[i] 的时候,arr[i + 1] 、arr[i + 2] 等相邻的数组元素也会被加载到 cache 中,而当下一次迭代中,需要读取数组元素 arr[i + 1] 时,就能直接从 cache 中取出,速度非常快。而因为以列读取数组时,arri 和 arri + 1 在内存中的位置就不再是紧密相连,而是相距一个数组行大小。这也导致了在读取 arri 时,arri + 1 并没有被加载到 cache 中。在下一次迭代时就会发生 cache miss 也就导致读取速度大幅下降。
prefetcher
如果我们不再是按某种顺序,而是随机地遍历数组,结果又会如何呢?
pub fn row_major_traversal(arr: &mut Vec<Vec<usize>>) {
let n = arr.len();
for i in 0..n {
assert!(arr[i].len() == n);
let ri: usize = rand::random();
std::intrinsics::black_box(ri);
for j in 0..n {
arr[i][j] += j;
}
}
}
pub fn column_major_traversal(arr: &mut Vec<Vec<usize>>) {
let n = arr.len();
for i in 0..n {
assert!(arr[i].len() == n);
let ri: usize = rand::random();
std::intrinsics::black_box(ri);
for j in 0..n {
arr[j][i] += j;
}
}
}
pub fn random_access(arr: &mut Vec<Vec<usize>>) {
let n = arr.len();
for i in 0..n {
assert!(arr[i].len() == n);
for j in 0..n {
let ri: usize = rand::random();
arr[j][ri % n] += j;
}
}
}理论上来说,随机遍历和按列遍历都会导致频繁地 cache miss ,所以两者的效率应该是相近的。接下来,我们进行 benchmark:
可以看到,random_access比 column_major 的效率还要低了 2 倍。原因是,在 cache 和 cpu 间还有 prefetcher
我们可以参考维基百科上的资料:
Cache prefetching can be accomplished either by hardware or by software.
- Hardware based prefetching is typically accomplished by having a dedicated hardware mechanism in the processor that watches the stream of instructions or data being requested by the executing program, recognizes the next few elements that the program might need based on this stream and prefetches into the processor's cache.
- Software based prefetching is typically accomplished by having the compiler analyze the code and insert additional "prefetch" instructions in the program during compilation itself.
而 random_access 会让 prefetching 的机制失效,使得运行效率进一步下降。
cache associativity
如果我们按照不同的步长迭代一个数组会怎么样呢?
pub fn iter_with_step(arr: &mut Vec<usize>, step: usize) {
let n = arr.len();
let mut i = 0;
for _ in 0..1000000 {
unsafe { arr.get_unchecked_mut(i).add_assign(1); }
i = (i + step) % n;
}
}steps 为:
let steps = [
1,
2,
4,
7, 8, 9,
15, 16, 17,
31, 32, 33,
61, 64, 67,
125, 128, 131,
253, 256, 259,
509, 512, 515,
1019, 1024, 1031
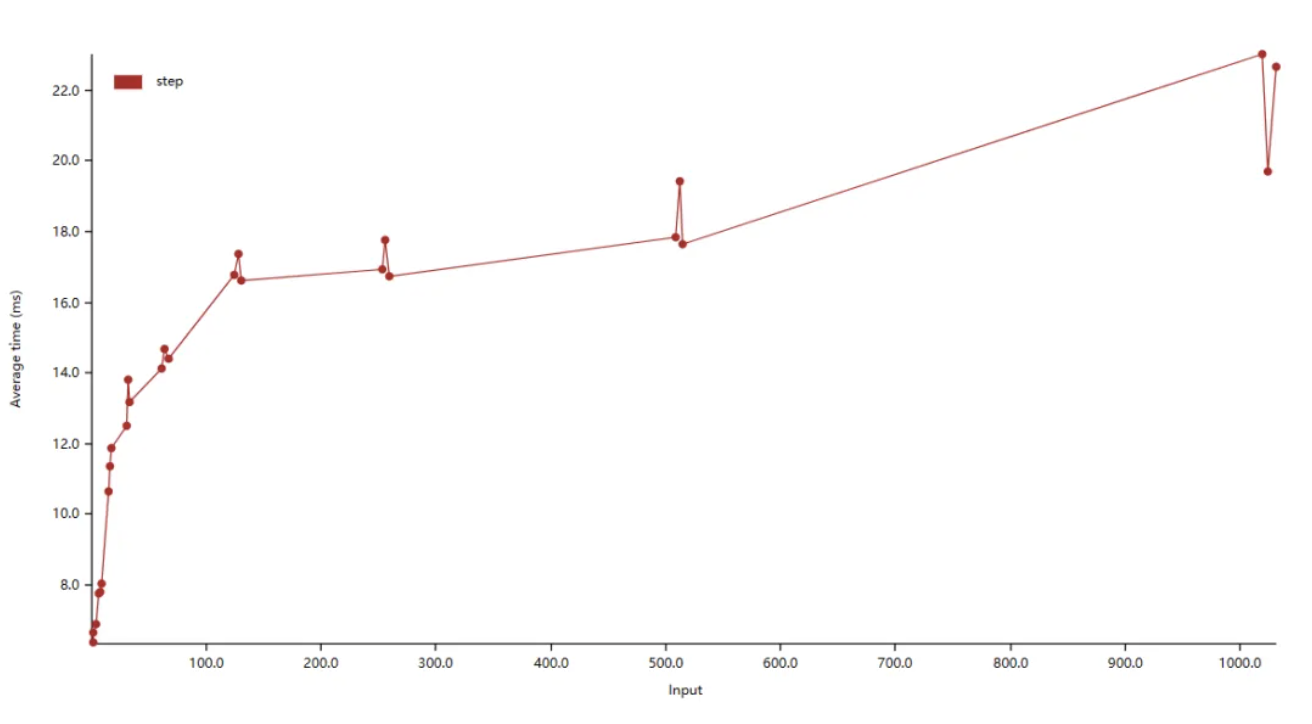
];我们进行测试:
可以看见当 step 为 2 的幂次时,都会有一个运行时间的突起,一个性能的毛刺。这是为什么呢?要回答这个问题,我们需要温习一些计组知识。
cache 的大小是要远小于主存的。这就意味着我们需要通过某种方式将主存的不同位置映射到缓存中。一般来说,共有 3 种不同的映射方式。
全相联映射
全相联映射允许主存中的行可以映射到缓存中的任意一行。这种映射方式灵活性很高,但会使得缓存的查找速度下降。
直接映射
直接映射则规定主存中的某一行只能映射到缓存中的特定行。这种映射方式查找速度高,但灵活性很低,会经常导致缓存冲突,从而导致频繁 cache miss 。
组相联映射
组相联映射则尝试吸收前两者的优点,将缓存中的缓存行分组,主存中某一行只能映射到特定的一组,在组内则采取全相联的映射方式。如果一组之内有 n 个缓存行,我们就称这种映射方式为 n 路组相联(n-way set associative)。
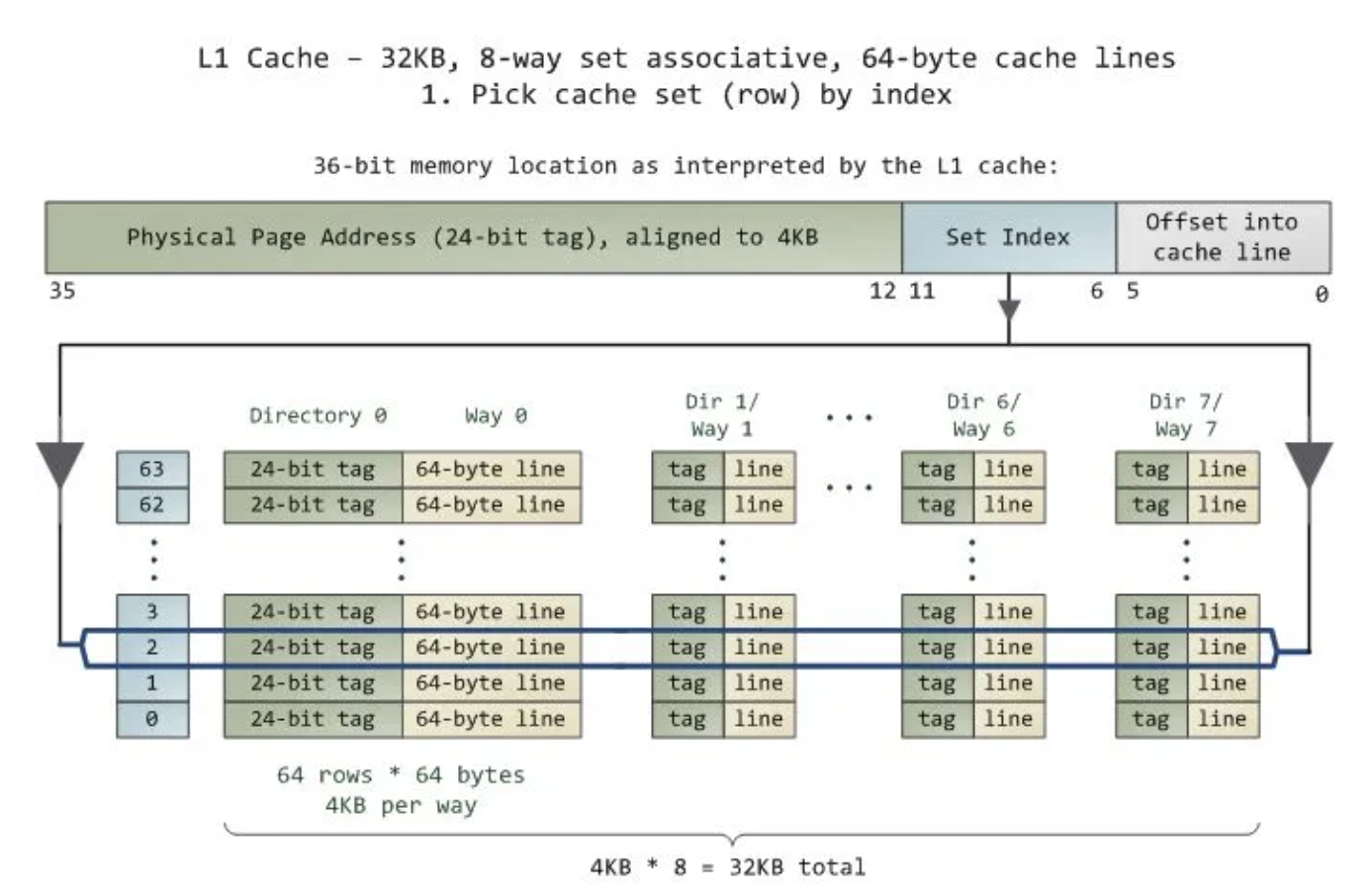
回到真实的 cpu 中,如:AMD Ryzen 7 4700u 。
我们可以看到,L1 cache 大小为 4 x 32 KB (128KB) ,采取 8 路组相联,缓存行大小为 64 bytes 。也就是说,该缓存共有 4x32x1024 byte/64 byte = 2048 行,共分为 2048/8 = 256 组。也就是说,当迭代数组的步长为 时,数据更可能会被分到同一个组内,导致 cache miss 更加频繁,从而导致效率下降。
(注:我的 cpu 是 intel i7-10750H ,算得的 L1 cache 的组数为 384 ,并不能很好地用理论解释。)
false share
我们再来观察一组 benchmark。
use std::sync::atomic::{AtomicUsize, Ordering};
use std::thread;
fn increase(v: &AtomicUsize) {
for _ in 0..10000 {
v.fetch_add(1, Ordering::Relaxed);
}
}
pub fn share() {
let v = AtomicUsize::new(0);
thread::scope(|s| {
let ta = s.spawn(|| increase(&v));
let tb = s.spawn(|| increase(&v));
let tc = s.spawn(|| increase(&v));
let td = s.spawn(|| increase(&v));
ta.join().unwrap();
tb.join().unwrap();
tc.join().unwrap();
td.join().unwrap();
});
}
pub fn false_share() {
let a = AtomicUsize::new(0);
let b = AtomicUsize::new(0);
let c = AtomicUsize::new(0);
let d = AtomicUsize::new(0);
thread::scope(|s| {
let ta = s.spawn(|| increase(&a));
let tb = s.spawn(|| increase(&b));
let tc = s.spawn(|| increase(&c));
let td = s.spawn(|| increase(&d));
ta.join().unwrap();
tb.join().unwrap();
tc.join().unwrap();
td.join().unwrap();
});
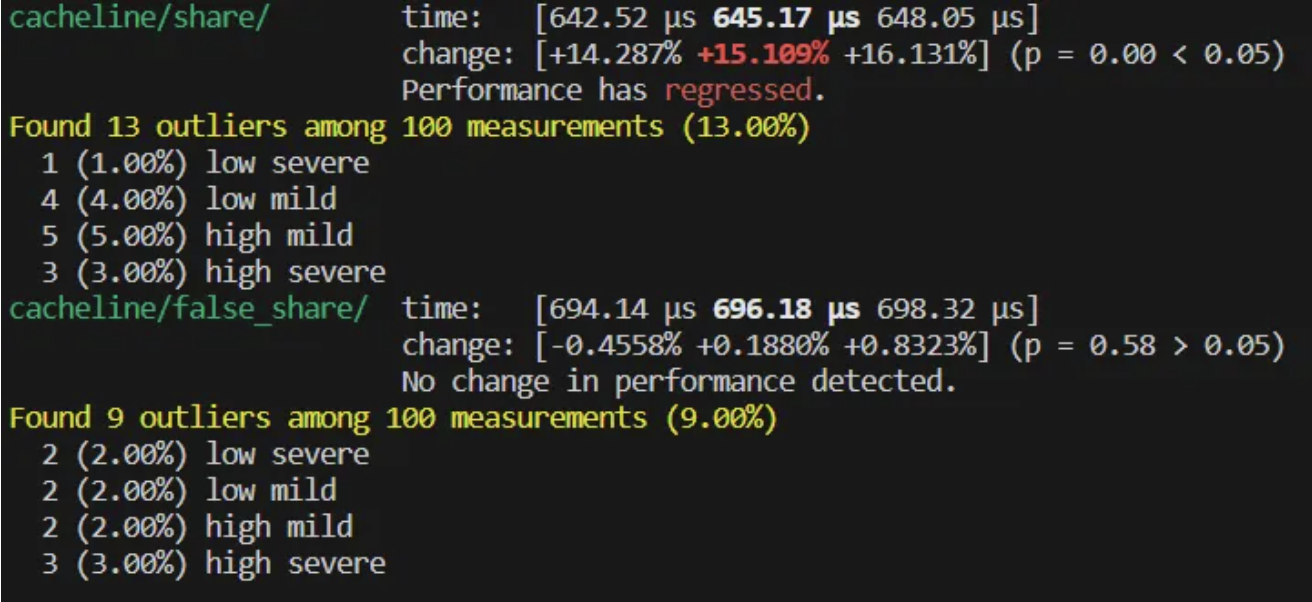
}在 share 函数中,四个线程同时竞争原子变量 v 。而在 false_share 函数中,四个线程分别操作不同的原子变量,理论上线程之间不会产生数据竞争,所以 false_share 的执行效率应该比 share 要高。但 benchmark 的结果却出乎意料:
可以看到 false_share 比 share 的执行效率还要低。
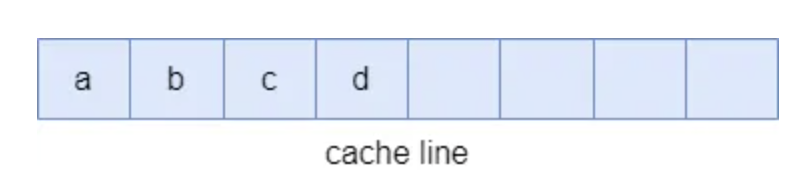
在前文中提到,cpu 在读取数据时,是以一个 cache line 大小为单位将数据从主存中加载到 cache 中的。在前文中提到,笔者机器的 cache line 大小为:64 bytes 。而 false_share 函数中,四个原子变量在栈中的排布可能是:
a, b, c, d 四个原子变量在同一个 cache line 中,也就是说实际上四个线程实际上还是发生了竞争,产生了 false share 的现象。
那要如何解决这个问题呢?我们可以采用 #[repr(align(64))] (在不同的编程语言中又不同的写法),告知编译器将原子变量的内存地址以一个 cache line 大小对齐,从而避免四个原子变量位于同一个 cache line 中。
fn increase_2(v: &AlignAtomicUsize) {
for _ in 0..10000 {
v.v.fetch_add(1, Ordering::Relaxed);
}
}
#[repr(align(64))]
struct AlignAtomicUsize {
v: AtomicUsize,
}
impl AlignAtomicUsize {
pub fn new(val: usize) -> Self {
Self { v: AtomicUsize::new(val) }
}
}
pub fn non_share() {
let a = AlignAtomicUsize::new(0);
let b = AlignAtomicUsize::new(0);
let c = AlignAtomicUsize::new(0);
let d = AlignAtomicUsize::new(0);
thread::scope(|s| {
let ta = s.spawn(|| increase_2(&a));
let tb = s.spawn(|| increase_2(&b));
let tc = s.spawn(|| increase_2(&c));
let td = s.spawn(|| increase_2(&d));
ta.join().unwrap();
tb.join().unwrap();
tc.join().unwrap();
td.join().unwrap();
});
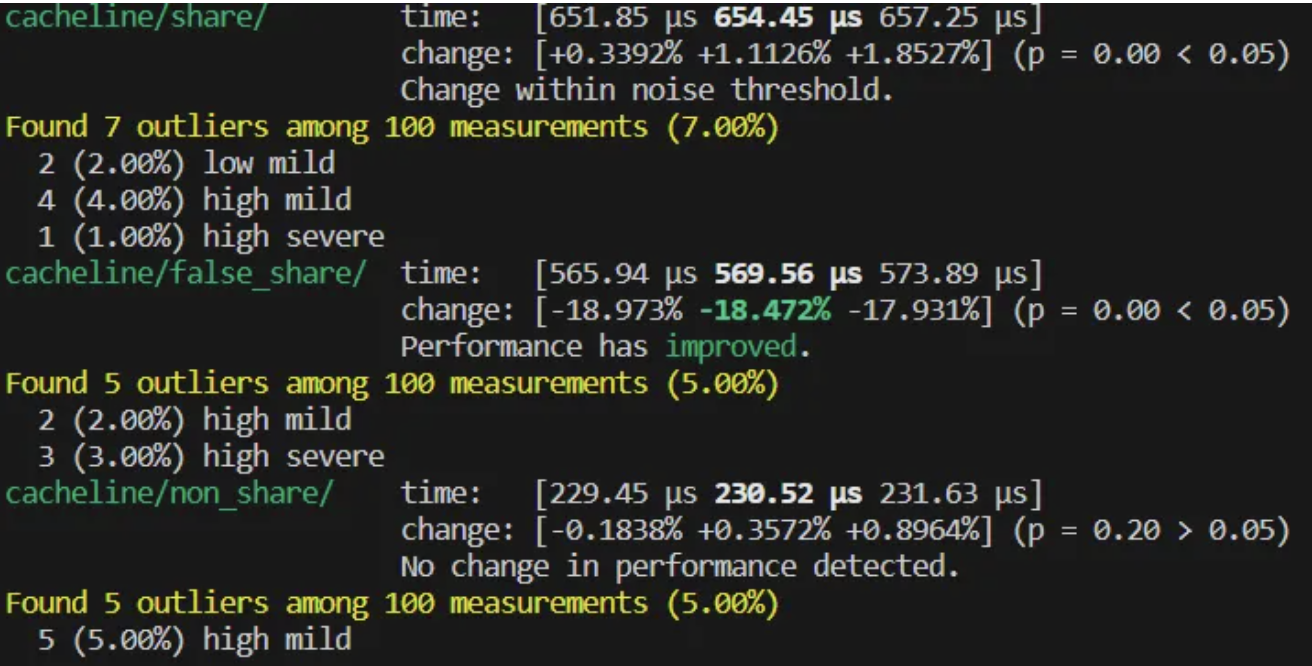
}我们再次进行 benchmark,这一次 benchmark 的结果就符合我们的预测了:
可以看见 non_share 相比前两者,提升了近乎两倍的效率。
pipeline
我们再看一个 benchmark:
pub trait Get {
fn get(&self) -> i32;
}
struct Foo { /* ... */ }
struct Bar { /* ... */ }
impl Get for Foo { /* ... */ }
impl Get for Bar { /* ... */ }
let mut arr: Vec<Box<dyn Get>> = vec![];
for _ in 0..10000 {
arr.push(Box::new(Foo::new()));
}
for _ in 0..10000 {
arr.push(Box::new(Bar::new()));
}
// 此时数组中元素的排列时有序的
arr.iter().filter(|v| v.get() > 0).count()
// 将数组打乱
arr.shuffle(&mut rand::thread_rng());
// 再次测试
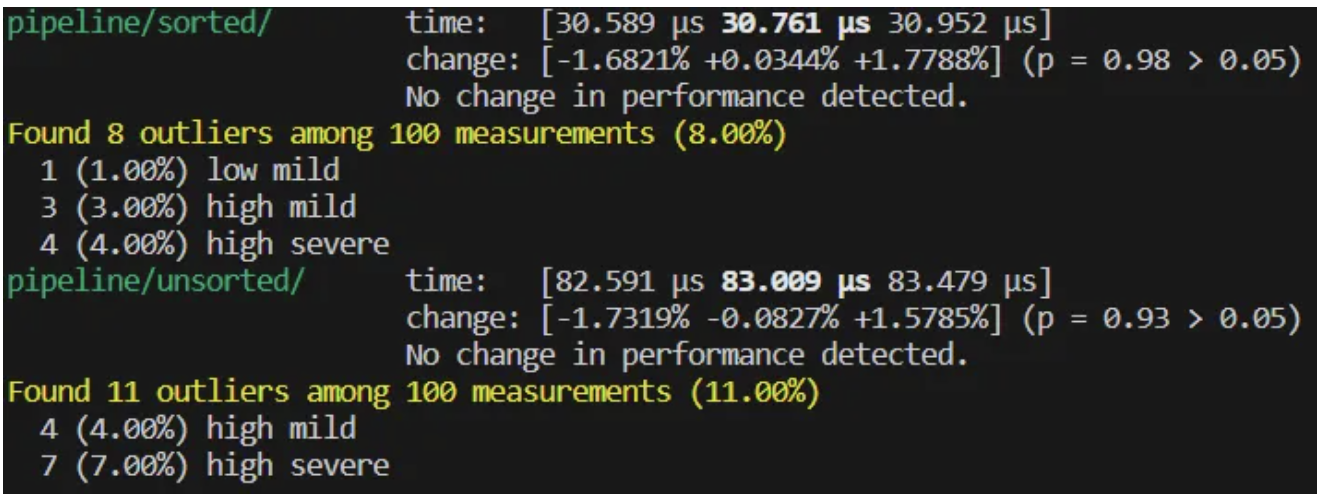
arr.iter().filter(|v| v.get() > 0).count()测试结果为:
可以看见,sorted 和 unsorted 之间效率差约 2.67 倍。这是因为频繁的分支预测失败导致的。
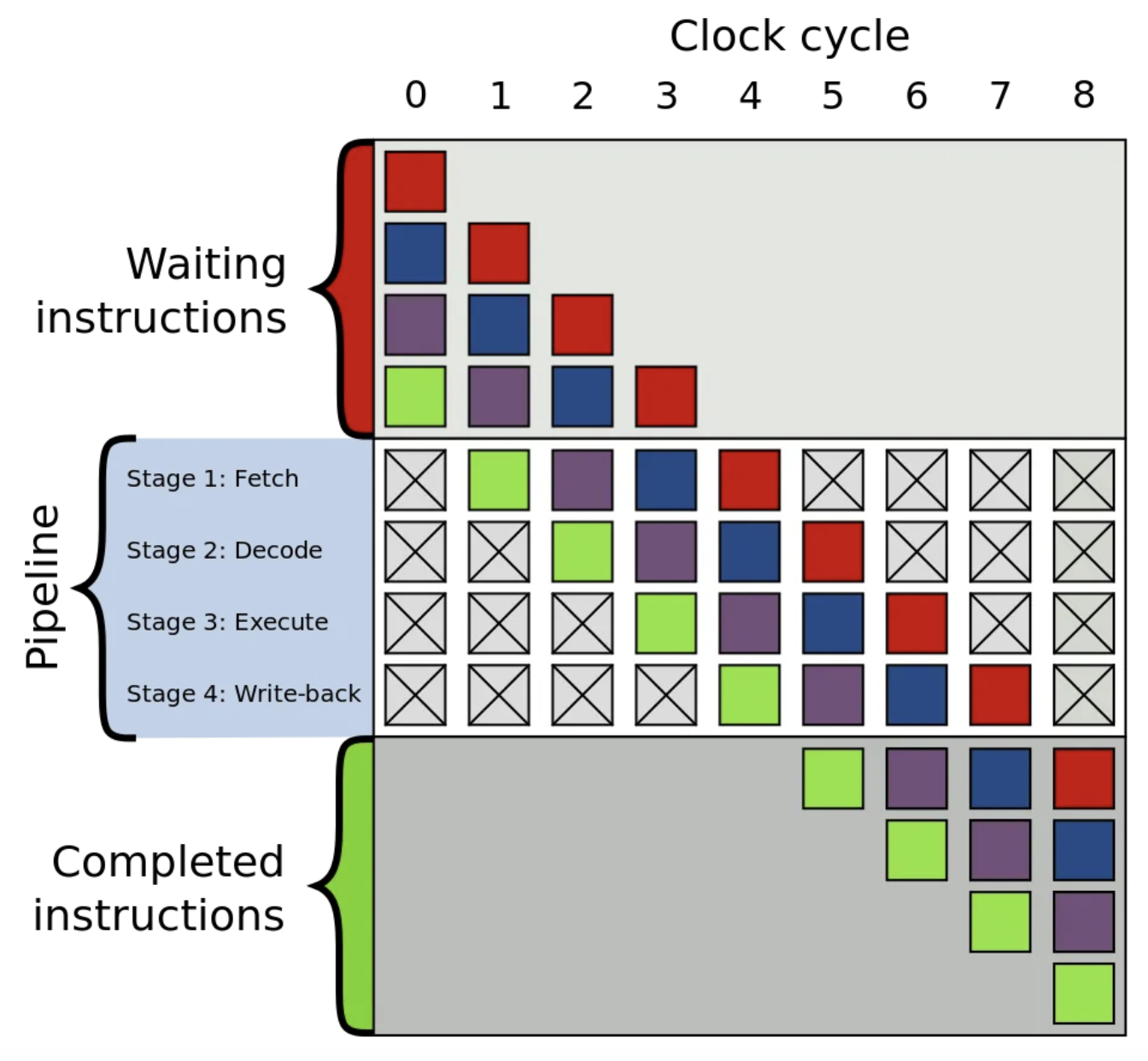
在CPU 中,每一条指令的执行都会分为多个步骤,而现代计算机架构中存在一个结构 pipeline 可以同时执行处于不同执行阶段的指令。
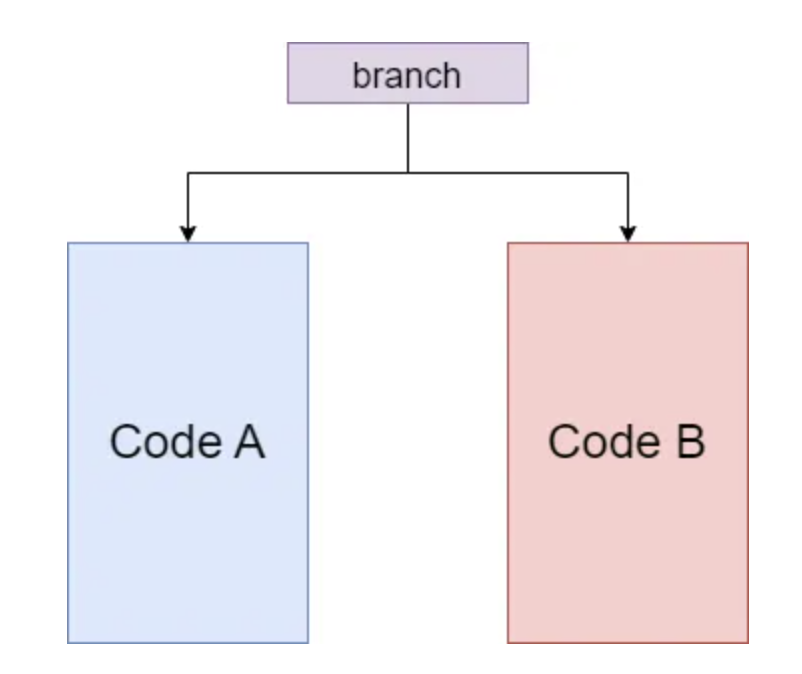
而 pipeline 要高效地工作,需要在执行指令 A 时就将接下来要执行的指令 B, C, D 等提前读入。在一般的代码中,pipeline 可以有效地工作,但遇到分支的时候,我们就遇到难题了:
如图,pipeline 应该读入 Code A 还是 Code B 呢?在执行分支语句前,谁也不知道,CPU 也是。如果我们还想要 pipeline 高效工作的话,我们就只剩下一条路:猜。只要猜得足够准,我们的效率就能够接近没有分支的情况。“猜”这一步也有一个专业名词——流水线冒险。而现代计算机在编译器配合以及一些算法的帮助下,某些分支(如下图所示)的预测成功率可以高达 99% 。
分支预测失败的代价是要付出代价的。首先,我们要清除 pipeline 中的指令,因为它们不是接下来要执行的指令。其次,我们要将接下来要执行的指令一一加载进 pipeline 。最后,指令经过多个步骤被执行。
在测试代码中,我们打乱数组后,就会导致分支预测频繁失败,最终导致了执行效率的下降。
数据依赖
我们再来看一段代码:
pub fn dependent(a: &mut Vec<i32>, b: &mut Vec<i32>, c: &Vec<i32>) {
assert!(a.len() == 100000);
assert!(b.len() == 100000);
assert!(c.len() == 100000);
for i in 0..=99998 {
a[i] += b[i];
b[i + 1] += c[i];
}
a[9999] += b[9999];
}
pub fn independent(a: &mut Vec<i32>, b: &mut Vec<i32>, c: &Vec<i32>) {
assert!(a.len() == 100000);
assert!(b.len() == 100000);
assert!(c.len() == 100000);
a[0] += b[0];
for i in 0..=99998 {
b[i + 1] += c[i];
a[i + 1] += b[i + 1];
}
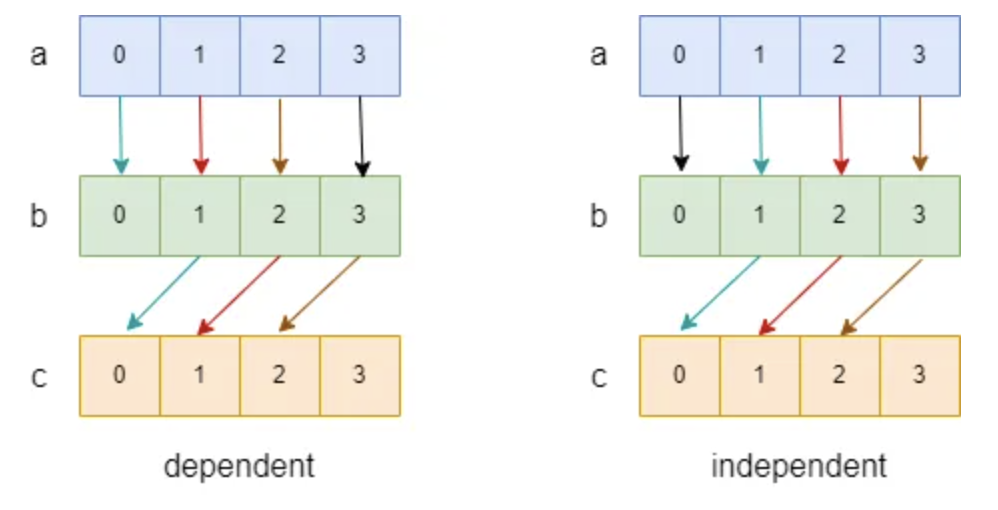
}在这段代码中,我们通过两种不同的方式迭代数组,并最终达成一致的效果。我们画出,数据流图如下图:
在上图中,我们用箭头表示依赖关系(a[0] -> b[0] 表示 a[0] 的结果依赖于 b[0] ),用黑色箭头表示在循环外进行的操作,用不同的颜色,表示不同迭代中的操作。我们可以看到,在 dependent 中,不同颜色的箭头会出现在同一个数据流中,如:(a[1]->b[1]->c[0] 中就出现了红色和蓝色箭头),这就意味着第 n + 1 次迭代会依赖于第 n 次迭代的结果,而 independent 中则没有这种情况。
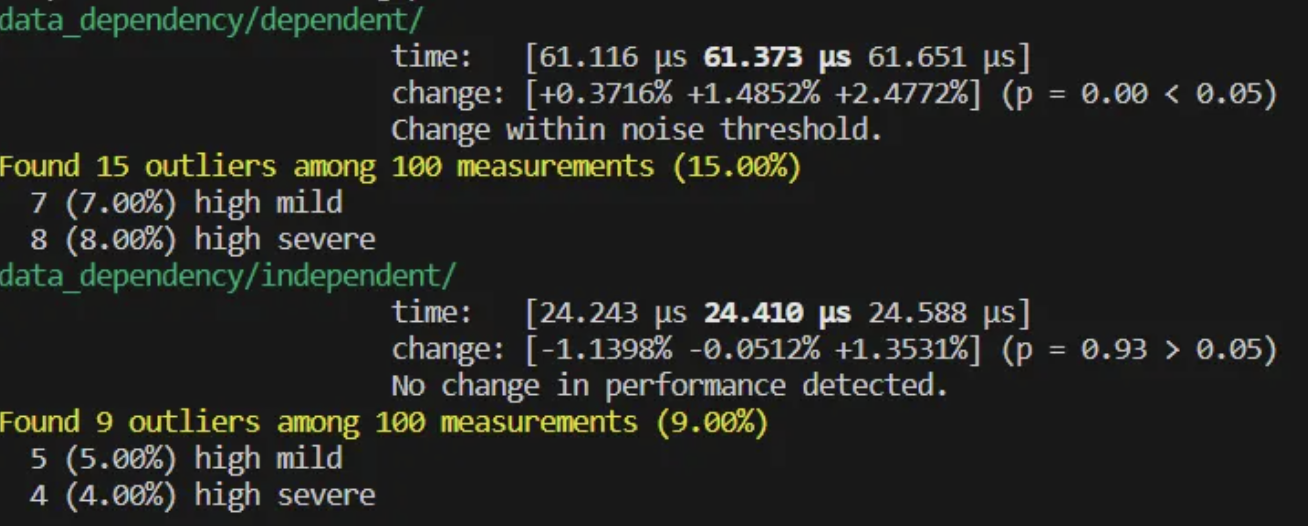
这会产生什么影响呢?我们来进行测试:
可以看到,出现了近 3 倍的效率差距。这有两方面原因。
一是数据依赖会导致 pipeline 效率以及 cpu 指令级并行的效率变低。
二是这种迭代之间的依赖会阻止编译器的向量化优化。我们观察等价的 cpp 代码(rust 1.71 的优化能力并不足以将 independet 向量化,我略感悲伤)。
#include <vector>
using i32 = int;
template<typename T>
using Vec = std::vector<T>;
void dependent(Vec<i32> &a, Vec<i32> &b, Vec<i32> &c) {
for (int i = 0; i < 9999; i++) {
a[i] += b[i];
b[i + 1] += c[i];
}
a[9999] += b[9999];
}
void independent(Vec<i32> &a, Vec<i32> &b, Vec<i32> &c) {
a[0] += b[0];
for (int i = 0; i < 9999; i++) {
b[i + 1] += c[i];
a[i + 1] += b[i + 1];
}
}查看汇编:
dependent(...):
mov rax, rdx
mov rdx, QWORD PTR [rsi]
mov rcx, QWORD PTR [rdi]
mov rdi, QWORD PTR [rax]
xor eax, eax
.L2:
mov esi, DWORD PTR [rdx+rax]
add DWORD PTR [rcx+rax], esi
mov esi, DWORD PTR [rdi+rax]
add DWORD PTR [rdx+4+rax], esi
add rax, 4
cmp rax, 39996
jne .L2
mov eax, DWORD PTR [rdx+39996]
add DWORD PTR [rcx+39996], eax
ret
independent(...):
mov rax, QWORD PTR [rdi]
mov rcx, rdx
mov rdx, QWORD PTR [rsi]
lea rdi, [rax+4]
mov esi, DWORD PTR [rdx]
add DWORD PTR [rax], esi
lea r8, [rdx+4]
mov rsi, QWORD PTR [rcx]
lea rcx, [rdx+20]
cmp rdi, rcx
lea rdi, [rax+20]
setnb cl
cmp r8, rdi
setnb dil
or ecx, edi
mov rdi, rdx
sub rdi, rsi
cmp rdi, 8
seta dil
test cl, dil
je .L9
mov rcx, rax
sub rcx, rsi
cmp rcx, 8
jbe .L9
mov ecx, 4
.L7:
movdqu xmm0, XMMWORD PTR [rsi-4+rcx]
movdqu xmm2, XMMWORD PTR [rdx+rcx]
paddd xmm0, xmm2
movups XMMWORD PTR [rdx+rcx], xmm0
movdqu xmm3, XMMWORD PTR [rax+rcx]
paddd xmm0, xmm3
movups XMMWORD PTR [rax+rcx], xmm0
add rcx, 16
cmp rcx, 39988
jne .L7
movq xmm0, QWORD PTR [rsi+39984]
movq xmm1, QWORD PTR [rdx+39988]
paddd xmm0, xmm1
movq QWORD PTR [rdx+39988], xmm0
movq xmm1, QWORD PTR [rax+39988]
paddd xmm1, xmm0
movq QWORD PTR [rax+39988], xmm1
mov ecx, DWORD PTR [rdx+39996]
add ecx, DWORD PTR [rsi+39992]
mov DWORD PTR [rdx+39996], ecx
add DWORD PTR [rax+39996], ecx
ret
.L9:
mov ecx, 4
.L6:
mov edi, DWORD PTR [rdx+rcx]
add edi, DWORD PTR [rsi-4+rcx]
mov DWORD PTR [rdx+rcx], edi
add DWORD PTR [rax+rcx], edi
add rcx, 4
cmp rcx, 40000
jne .L6
retAI助手可以看到,independent 函数被成功向量化。
作者:腾讯程序员
文章来源:腾讯技术工程
推荐阅读
更多腾讯AI相关技术干货,请关注专栏腾讯技术工程 欢迎添加极术小姐姐微信(id:aijishu20)加入技术交流群,请备注研究方向。