在过去的几个月中,时间序列基础模型的发展速度一直在加快,每个月都能看到新模型的发布。从TimeGPT 开始,我们看到了 Lag-Llama 的发布,Google 发布了 TimesFM,Amazon 发布了 Chronos,Salesforce 发布了 Moirai。TimesFM是信息最多的模型,而Lag-Llama、Chronos我们都做过详细的介绍。今天我们来详细介绍一下Moirai,这里可能最不知名(相对)就是Salesforce了,所以基本没有介绍 Moirai的文章,我们就来补足这个信息。
首先零样本推理这一概念源于这样一个想法:尽管模型在训练期间没有从特定任务或数据领域中“看到”任何示例,但它仍能有效地在那一领域内执行任务。这一术语最初由 Hinton 等人在 2009 年的 NIPS 会议上提交的论文“零样本学习与语义输出代码”中引入。从那时起,它已经成为最突出的研究主题之一,并现在开始进入时间序列分析领域。
在本文中,我们将探索用于时间序列预测的 Salesforce 新发布的基础模型 Moirai。最后我们还对比Moirai 与其他两个基础模型之间的差异,例如训练数据的大小、模型参数的数量以及它们是否允许多变量预测。最后还将介绍实际实施的细节,并彻底分析模型的性能,然后使用一个公共数据集比较 Moirai 与 TiDE 和 Chronos 的性能。
背景
我们介绍一些时间序列预测的关键概念,以便更容易理解 Moirai 所提出解决的时间序列问题。
单变量时间序列预测侧重于使用单一时间序列变量的过去值来预测其未来值。预测模型依赖于该单一变量的历史数据来识别可以用来进行未来预测的模式、趋势和周期。例如,仅根据过去的温度记录来预测明天的温度。
多变量时间序列预测涉及基于历史数据预测多个相关时间序列变量的未来值。在这种情况下,预测模型会考虑多个变量之间的相互依赖性和交互作用来进行预测。例如,预测产品的未来销售量可能不仅考虑过去的销售情况,还可能考虑市场支出、季节趋势和竞争对手的价格等相关因素。
时间序列预测中的协变量是可以影响预测结果的变量。这些变量可以提前知道或预估。在单变量和多变量预测模型中,协变量引入了目标变量历史数据之外的额外见解。例如,假日、特殊事件和经济指标等因素。此外,在多变量预测中,协变量扩展到包括相关的时间序列数据——这些可能是已知未来值或需要预测的变量(参见上述例子)。
时间序列频率指的是时间序列中数据点的记录或观察间隔,代表了数据随时间的规律性和粒度。这种频率可以从高频数据(如金融市场中的分钟级交易)到低频数据(如年度经济指标)不等。不同的频率可以捕捉到各种趋势、模式和季节性。例如日常销售数据可能揭示出月度汇总中看不到的模式,如每周周期或特定日的影响。
概率预测不仅仅提供点预测,还提供可能的未来结果分布。这些输出分布代表了不同未来值发生的可能性,允许在不确定性下进行更加明智的决策。比如说在观测值严格为正的情况下,如销售量或能耗,概率预测可能使用对数正态或伽玛分布来模拟可能结果的范围。概率预测在风险管理和规划中特别有用,因为它使利益相关者能够评估从最悲观到最乐观的各种情景的可能性。
Moirai
Moirai 是 Salesforce 开发的用于时间序列预测的基础模型。它被设计为一种通用模型,能够预测广泛的时间序列。为了实现这种灵活性,该模型解决了时间序列数据相关的几个挑战,包括:
- 处理各种数据频率(小时、日、周等);
- 适应任何数量和类型的协变量,无论它们在未来是否已知;
- 使用灵活的分布生成概率预测,可适应多种情况。
数据集是任何基础模型的核心组成部分。作者构建了一个大规模且多样化的数据集,包含了270亿观测值,涵盖了九个不同的时间序列领域。另外他们还引入了三个主要的新概念:多尺寸补丁投影层(Multi Patch Size Projection Layers)、任意变量注意力(Any-Variate Attention)和混合分布(Mixture Distribution),每个概念我们都将在下面详细解释。
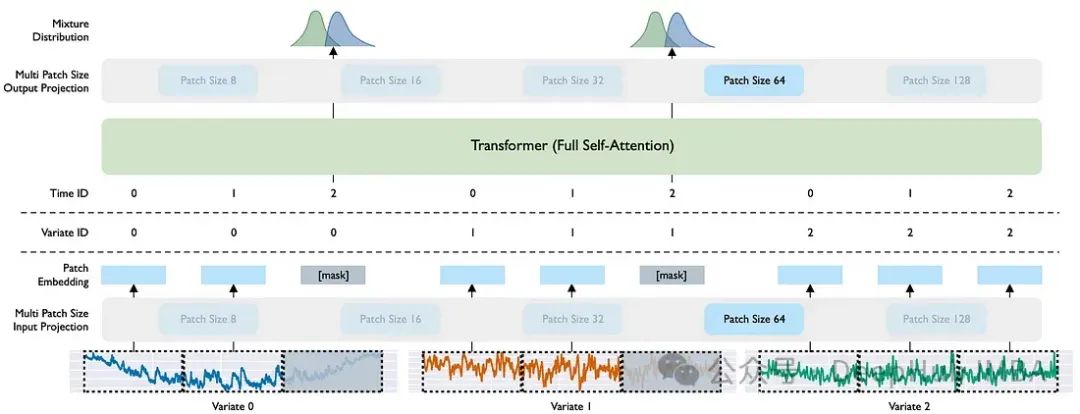
1、多尺寸补丁投影层(Multi Patch Size Projection Layers)
补丁这个概念首次被引入到时间序列中是 PatchTST [7]。其目的是将时间序列数据分割成大小为 P 的补丁,这些补丁是原始序列的较短子集。在时间序列预测的基础模型中,补丁的作用是什么呢?
时间序列预测的目标是理解每个不同时间步之间的相关性。基础模型倾向于使用基于transformer 的架构。虽然transformer 在自然语言处理应用中表现良好,但是单个时间步骤并没有像句子中的单词那样的语义意义。所以我们需要一种方法来提取局部语义信息,以应用注意力机制。补丁化序列将时间步聚合到具有更丰富语义表征的子序列级组件中。
也就是说,像词嵌入在高维空间中表示单词一样,时间序列补丁可以被视为在其特征定义的多维空间中表示序列段的表征。
这个过程带来了许多优势,例如:
- 使注意力机制能够通过观察一组时间序列而不是单个时间步来提取局部语义意义;
- 减少了输入到编码器的标记数量,从而减少了所需的内存,允许向模型提供更长的输入序列;
- 有了更长的序列,模型有更多的信息可供处理,能够提取更有意义的时间关系,可能产生更准确的预测。
论文使用的补丁大小取决于数据频率,其中低频率数据具有较小的补丁,高频率数据具有较大的补丁大小:
年度和季度 → 补丁大小 8
月度 → 补丁大小 8, 16, 32
周和日 → 补丁大小 16, 32
小时 → 补丁大小 32, 64
分钟级 → 补丁大小 32, 64, 128
秒级 → 补丁大小 64, 128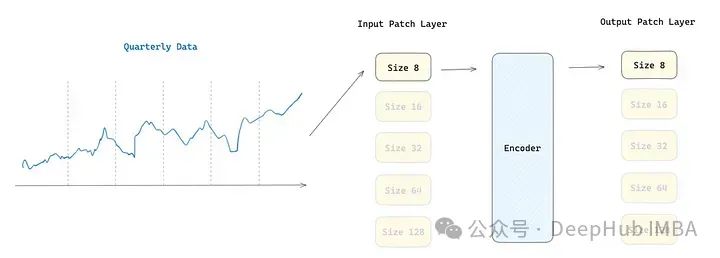
作者使用了输入和输出补丁层。在数据转换成补丁后,输入补丁层是一个将时间序列子集映射成补丁嵌入简单的线性层,第二个补丁层用于处理编码器的输出。输出标记随后通过多尺寸输出投影进行解码。由于存在五种不同的补丁大小,模型具有五个不同的输入补丁层和五个不同的输出补丁层,根据处理输入数据的补丁大小来激活。
2、任意变量注意力(Any-Variate Attention)
传统的transformer架构期望接收一系列目标值,模型预期要处理多序列目标值和动态协变量的多变量时间序列场景,所以作者引入了任意变量注意力,允许 Moirai 处理多个序列。
这个过程从将多个时间序列(变量)展平成一个值序列开始。然后应用变量编码来允许模型区分序列中的不同变量,这在计算注意力得分时很重要。
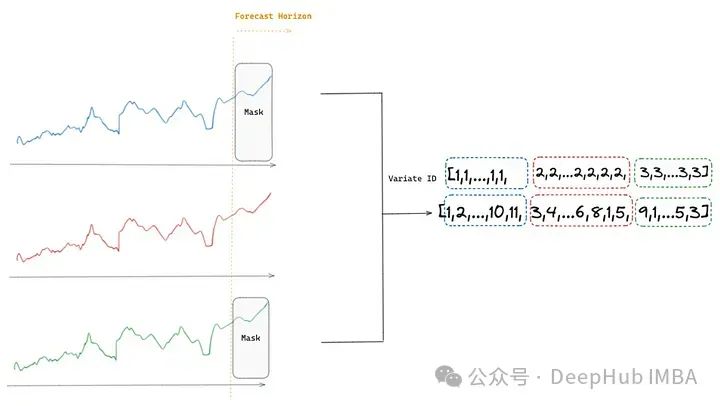
任意变量注意力有两个基本特性:它实现了关于变量顺序的排列等变性和关于变量索引的排列不变性。
变量顺序的排列等变性:如果在一个变量内的观测序列被排列,模型对该变量的输出将反映相同的排列。这一属性是必需的,因为我们正在处理时间序列,且每个变量内的时间动态必须被保留,所以模型对时间序列动态的理解无论输入顺序如何都是一致的。
变量索引的排列不变性:如果变量被重新排序,模型的输出不会改变。比如说考虑一个处理温度和湿度数据作为多变量时间序列设置中的两个变量的场景。如果我们决定交换向模型呈现这些变量的顺序(首先是湿度,然后是温度,而不是首先是温度,然后是湿度),这不应影响最终输出。模型将变量索引视为可互换的,而专注于编码的关系。
为了实现排列等变性/不变性,Moirai 使用了两种不同的方法:
- 旋转位置嵌入(RoPE)[8] 确保通过其编码方式实现排列等变性。它通过在嵌入空间中旋转标记的表征来编码位置信息。旋转角度与序列中每个标记的位置成比例。它在保持任何一对标记之间的相对距离的同时捕获了每个标记的绝对位置。
- 二进制注意力偏差允许模型实现不变性 —— 将变量视为无序的。模型通过根据元素是否属于同一变量(m=n)或不同变量(m≠n)应用不同的注意力偏差(可学习的标量)动态调整其焦点。这使得任意变量注意力机制能够处理任意数量的变量及其排列。

3、混合分布(Mixture Distribution)
Moirai 是一个概率预测模型,这意味着它学习的是分布的参数,而不仅仅是提供一个单一的点预测。输出作为分布,使决策者能够评估预测的不确定性,因为更宽的区间表明模型的不确定性更大。
与其他概率模型如 DeepAR [9] 类似,DeepAR 可以配置为估计高斯、Beta、负二项或学生 t 分布的参数。Moirai 的目标是通过最小化损失函数,特别是负对数似然,来估计概率分布的参数。
由于 Moirai 是一个基础模型,它旨在预测各种数据域,因此不能限于单一分布。为了适应所有可能的情况,模型学习的是多种分布的混合,每种都适合不同类型的数据:
- 学生 t 分布是大多数时间序列的稳健选择,因为它能够处理离群值和具有较重尾部的数据。
- 负二项分布对于严格正的计数数据很有用,因为它不预测负值。
- 对数正态分布有效地预测右偏数据,如经济指标或自然现象。
- 低方差正态分布适用于紧密围绕平均值聚集的数据,适用于高置信度预测。

TimeGPT、Chronos、Moirai 比较
虽然我认为TimeGPT上不了台面,但是作为第一个将基础模型概念提出来的作品,我们还是要说 明一下
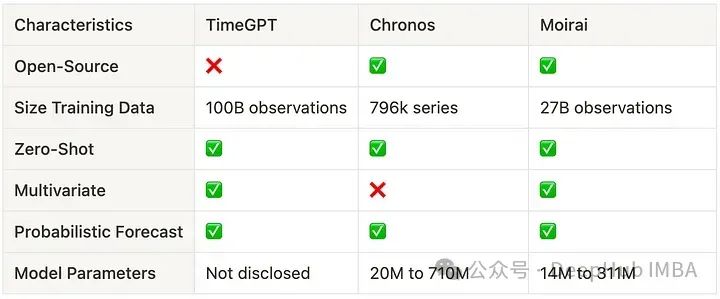
上表比较了基础模型的关键特征。这里我们并不关注它们的性能比较因为这将在下一节中讨论。我们应该首先说明,Chronos 和 Moirai 是开源模型,另外就是Chronos 显示出更好的数据效率,需要的训练数据显著少,但是他的最大问题是尚未支持多变量。通过查看参数数量,可以看到时间序列模型比大型语言模型(LLM)要小得多,这使它们更易于使用和部署。
性能对比
最后我们使用 Moirai 预测澳大利亚旅游访客数量,然后与 Chronos(大版本)和 TiDE 进行比较
我们对数据集进行了增强,添加了经济协变量(例如CPI、通胀率、GDP),这些协变量从 Trading Economics 提取,这都是基于官方来源的经济指标。我们还对数据集进行了一些预处理,进一步提高数据的可用性。
我们首先导入库并设置全局变量。设置日期列、目标列、动态协变量、序列的频率以及预测的时间范围。
%load_extautoreload
%autoreload2
importtorch
importpandasaspd
importnumpyasnp
importutils
fromdatasetsimportload_dataset
fromgluonts.dataset.pandasimportPandasDataset
fromhuggingface_hubimporthf_hub_download
fromuni2ts.model.moiraiimportMoiraiForecast
TIME_COL="Date"
TARGET="visits"
DYNAMIC_COV= ['CPI', 'Inflation_Rate', 'GDP']
SEAS_COV=['month_1', 'month_2', 'month_3', 'month_4', 'month_5', 'month_6', 'month_7','month_8', 'month_9', 'month_10', 'month_11', 'month_12']
FORECAST_HORIZON=8# months
FREQ="M"然后加载我们的数据集
# load data and exogenous features
df=pd.DataFrame(load_dataset("zaai-ai/time_series_datasets", data_files={'train': 'data.csv'})['train']).drop(columns=['Unnamed: 0'])
df[TIME_COL] =pd.to_datetime(df[TIME_COL])
# one hot encode month
df['month'] =df[TIME_COL].dt.month
df=pd.get_dummies(df, columns=['month'], dtype=int)
print(f"Distinct number of time series: {len(df['unique_id'].unique())}")
df.head()分割数据(使用最近8个月的数据作为测试集)。
# 8 months to test
train=df[df[TIME_COL] <= (max(df[TIME_COL])-pd.DateOffset(months=FORECAST_HORIZON))]
test=df[df[TIME_COL] > (max(df[TIME_COL])-pd.DateOffset(months=FORECAST_HORIZON))]
print(f"Months for training: {len(train[TIME_COL].unique())} from {min(train[TIME_COL]).date()} to {max(train[TIME_COL]).date()}")
print(f"Months for testing: {len(test[TIME_COL].unique())} from {min(test[TIME_COL]).date()} to {max(test[TIME_COL]).date()}")
#Months for training: 220 from 1998–01–01 to 2016–04–01
#Months for testing: 8 from 2016–05–01 to 2016–12–01最后,我们需要将 pandas 转换为 GluonTS 数据集以供模型使用:
# create GluonTS dataset from pandas
ds=PandasDataset.from_long_dataframe(
pd.concat([train, test[["unique_id", TIME_COL]+DYNAMIC_COV+SEAS_COV]]).set_index(TIME_COL), # concatenaation with test dynamic covaraiates
item_id="unique_id",
feat_dynamic_real=DYNAMIC_COV+SEAS_COV,
target=TARGET,
freq=FREQ
)有了数据集,我们就可以使用Moirai进行预测。首先需要从Hugging Face加载模型并设置以下参数:
Prediction_length—这是我们之前定义的预测范围。
Context_length—模型可以处理序列中的多少项(任意正整数)。
Patch_size—每个补丁的长度。作者根据频率设置了不同的补丁大小。要使用预定义的值,patch_size应该设置为' auto '。它也可以设置为{auto, 8,16,32,64,128}中的任何值。
# Prepare pre-trained model by downloading model weights from huggingface hub
model=MoiraiForecast.load_from_checkpoint(
checkpoint_path=hf_hub_download(
repo_id="Salesforce/moirai-R-large", filename="model.ckpt"
),
prediction_length=FORECAST_HORIZON,
context_length=24,
patch_size='auto',
num_samples=100,
target_dim=1,
feat_dynamic_real_dim=ds.num_feat_dynamic_real,
past_feat_dynamic_real_dim=ds.num_past_feat_dynamic_real,
map_location="cuda:0"iftorch.cuda.is_available() else"cpu",
)
predictor=model.create_predictor(batch_size=32)
forecasts=predictor.predict(ds)
# convert forecast into pandas
forecast_df=utils.moirai_forecast_to_pandas(forecasts, test, FORECAST_HORIZON, TIME_COL)预测完成我们绘制出真值和预测的对比图。
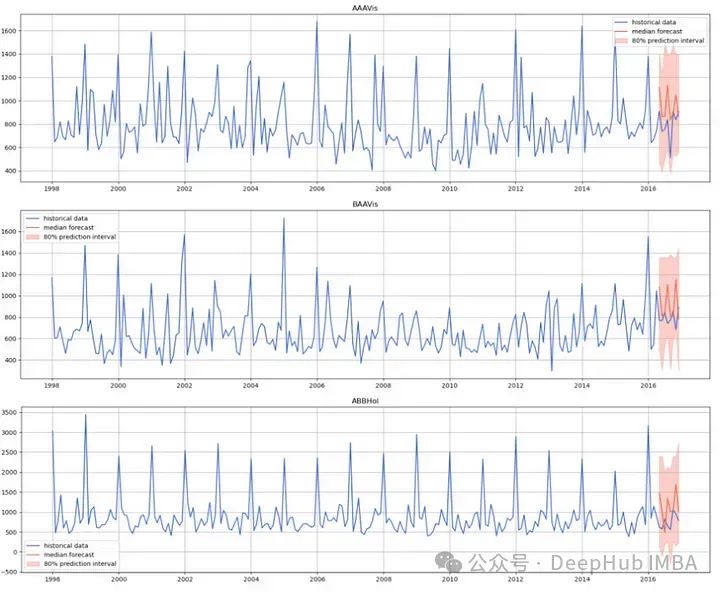
上显示了 Moirai 在预测我们的时间序列时的表现,其未能生成稳定的预测,它预测了多个连续的跳跃,幅度大于预期。
现在可以我们加载 TiDE 和 Chronos 生成的预测,并计算预测性能指标以进行比较。这里使用了平均绝对百分比误差(MAPE)作为比较指标。
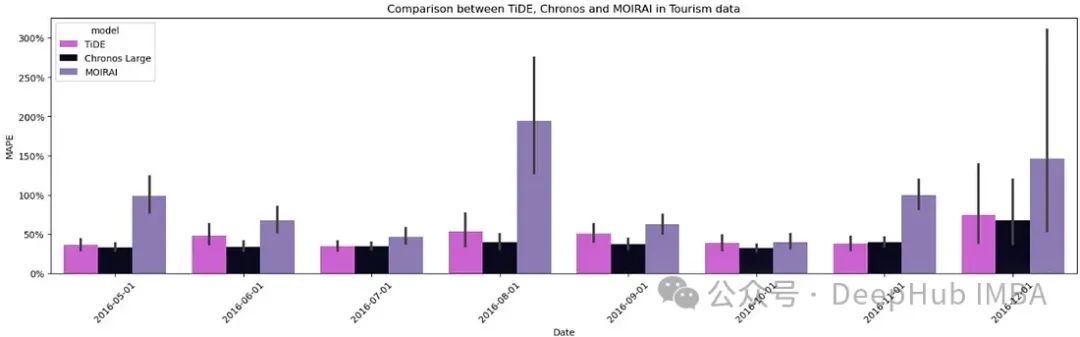
Moirai 在整个预测期内的 MAPE 最高。它在一个月中的表现略优于 TiDE,但从未能超过 Chronos。然后我又在几个私有数据集上进行了类似的实验,结果与上图呈现的一致。这种一致性在分析基础模型时很重要,因为训练数据集并未公开,而任何公共领域的数据集都可能被用于它们的训练数据。所以在这种情况下可以证明模型的性能。
另外就是Chronos 不允许使用协变量,并假设时间序列之间是独立的。所以结果表明 Chronos 的方法明显更好,未来有更大的改进潜力。
总结
在本文中,介绍了 Moirai并且与Chronos 和 TimeGPT进行了对比。
并且通过实验表明,Moirai 在与 TiDE 和 Chronos 的比较中未能表现出更优的性能。当比较 Moirai 和 Chronos 的性能时,我们预期 Moirai 由于能够通过动态协变量访问外部信息,并且是一个能够从不同序列间的交叉关系中受益的多变量时间序列模型,应有相当甚至更优的表现。但得到的结果却相反,这可能是因为模型过拟合了训练数据。
但是还是我们上次说的那句话,时间序列预测的基础模型开发竞赛才刚刚开始,我们将密切关注其进展,希望有更多的模型供我们学习和使用。
Unified Training of Universal Time Series Forecasting Transformers
https://arxiv.org/abs/2402.02592
其他引用
[1] Garza, A., & Mergenthaler-Canseco, M. (2023). TimeGPT-1. arXiv.2310.03589
[2] Rasul, K., Ashok, A., Williams, A. R., Ghonia, H., Bhagwatkar, R., Khorasani, A., Darvishi Bayazi, M. J., Adamopoulos, G., Riachi, R., Hassen, N., Biloš, M., Garg, S., Schneider, A., Chapados, N., Drouin, A., Zantedeschi, V., Nevmyvaka, Y., & Rish, I. (2024). Lag-Llama: Towards Foundation Models for Probabilistic Time Series Forecasting. arXiv. 2310.08278
[3] Das, A., Kong, W., Sen, R., & Zhou, Y. (2024). A decoder-only foundation model for time-series forecasting. arXiv. 2310.10688
[4] Ansari, A. F., Stella, L., Turkmen, C., Zhang, X., Mercado, P., Shen, H., Shchur, O., Rangapuram, S. S., Arango, S. P., Kapoor, S., Zschiegner, J., Maddix, D. C., Mahoney, M. W., Torkkola, K., Wilson, A. G., Bohlke-Schneider, M., & Wang, Y. (2024). Chronos: Learning the Language of Time Series. arXiv. 2403.07815
[5] Woo, G., Liu, C., Kumar, A., Xiong, C., Savarese, S., & Sahoo, D. (2024). Unified Training of Universal Time Series Forecasting Transformers. arXiv.2402.02592
[6] Palatucci, M., Pomerleau, D., Hinton, G. E., & Mitchell, T. M. (2009). Zero-shot Learning with Semantic Output Codes. In Y. Bengio, D. Schuurmans, J. Lafferty, C. Williams, & A. Culotta (Eds.), Advances in Neural Information Processing Systems (Vol. 22). Curran Associates, Inc.
[7] Yuqi Nie, Nam H. Nguyen, Phanwadee Sinthong, Jayant Kalagnanam. A Time Series is Worth 64 Words: Long-term Forecasting with Transformers. arXiv:2211.14730, 2022.
[8] Jianlin Su, Yu Lu, Shengfeng Pan, Ahmed Murtadha, Bo Wen, Yunfeng Liu. RoFormer: Enhanced Transformer with Rotary Position Embedding. arXiv:2104.09864, 2021.
[9] David Salinas, Valentin Flunkert, Jan Gasthaus. DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks. arXiv:1704.04110, 2017.
https://avoid.overfit.cn/post/7caa50443ff5472e8d3c7af347a30510


