为二值神经网络扩展 NPU 二值 GEMM 核心功能单元和编译器

二值化神经网络（BNNs）是将深度神经网络模型部署到资源受限设备上的最有前景的方法之一。然而，对于现代 BNNs（尤其是使用缩放因子和残差连接来最大化网络性能的 BNNs），在编译器和可编程加速器方面的支持非常有限。

本文提出了一种扩展神经处理单元（NPU）和编译器的方法，以支持现代二值化神经网络（BNNs）。通过批归一化折叠、高效处理少输入通道卷积和位打包流水线等优化手段，显著提升了二值卷积层的速度，并在 BiRealNet-18 模型上取得了 3.6∼5.5 倍的端到端性能提升。

1. 引言

人们对低精度神经网络的兴趣日益增加，这不仅是因为模型尺寸更小和计算需求更低所带来的效率提升，还因为量化和二值化神经网络在训练方面取得了进展。据报道，三或两位量化的模型在 ImageNet 分类任务中达到了基线性能（即浮点推理精度），甚至二值化神经网络也报告了类似的结果。

然而，对于这种极低精度的神经网络，架构和编译器的支持却不足。特别是，虽然二值化神经网络（BNNs）可以在 CPU 上使用位运算和计数指令运行，但由于CPU 上位运算的并行度有限，加速效果会受到限制。另一方面，FPGAs 可以提供非常大的并行度来加速二值化层，但它们通常（i）不灵活，意味着它们产生仅支持特定 BNN 的硬连线设计，以及（ii）难以支持先进的 BNNs（例如 BiRealNet 和 ReActNet），这些网络由于使用缩放因子和残差连接而显示出接近浮点精度的准确性。

因此，针对先进的 BNNs，本文提出了一种可编程的 NPU（神经处理单元）架构和编译器，它们既灵活又高效。

有几个挑战是在可编程 NPU 架构上加速先进 BNNs。

首先，如何在指令级别添加对二值操作的支持——无论是新的二值 MVM（矩阵-向量乘法）指令还是新的 MVM 核心等。由于最近的 BNNs 二值化了大部分但并非所有计算，因此仍有一些显著的计算需要多比特精度，例如残差连接。因此，我们需要同时支持整数 MVM 和二值 MVM，后者基于 XNOR-popcount，而前者基于数字乘法器和加法器。
其次，加速二值卷积层可能会使其他层成为性能瓶颈。因此，我们需要优化所有层，以便从加速二值卷积层中获益。
第三，我们在先进 BNNs（这些网络依赖缩放因子来实现高推理精度）的背景下重新审视批归一化（BN）层，并提出了一种简单而精确且高效的方法来在先进 BNNs 中实现 BN 层。

本文做出以下贡献：

提出了一种针对具有标量因子的二值化层的批归一化折叠方法。
提出了一种针对输入通道较少的卷积层（例如图像处理 CNNs 中的第一卷积层）的新型 reshape 方法。
提出了一种可以隐藏内存访问和位打包延迟的流水线方法。
已经实现了并评估了对编译器和 NPU 架构的扩展，它们共同高效地支持先进的二值化神经网络。

2. 背景与相关工作

A. 二值化神经网络

BNN [11] 是一种神经网络，其中激活函数和权重被限制在 {−1, 1}。二值化层可以按如下方式计算（省略偏置加法）：

B. 以往工作

以往关于 BNN 加速的工作大致可分为两类：硬件加速器生成器和通用处理器的编译器。首先，硬件加速器生成器（如 FINN [8] 和 FP-BNN [9]）采用模型描述并生成 BNN 加速器设计。

例如，FINN 编译器采用 BNN 模型描述并生成实现 BNN 模型的 HLS 代码。尽管 FINN 的最新版本也支持 QNNs，但它有两个重要限制：

它只支持流式架构，其中所有层都实现为专用硬件块，这可以实现非常高的吞吐量，但在模型架构方面可扩展性非常有限；
它不支持残差连接或缩放因子，因此无法支持先进的 BNNs。

其次，通用处理器（GPPs）的编译器（如 BMXNet [13]、daBNN [14]、Riptide [15] 和 Larq [16]）是编译器/工具链，用于在某些嵌入式处理器（例如 ARM）上生成快速高效的推理软件实现。虽然它们与我们的编译器相关，但它们根本无法支持神经处理单元。

更通用的神经网络编译器框架（如 TVM [17] 和 Glow [18]）可以支持 CPU、GPU 和 NPU（例如 VTA [10]），但它们目前不支持 NPU 上的位运算或二值卷积。（VTA 也不支持位运算/计数操作。）因此，如果不扩展编译器框架，对 BNNs 的优化将相当有限。

虽然 BNN 是神经网络的一种极度量化的形式，但在硬件实现过程中可以进一步优化，例如累加器宽度最小化 [19] 和基于模拟交叉阵列的实现 [20]，但这些方法针对特定网络，可能不适合可编程 NPU。

本文的工作采用硬件/软件协同设计方法，定制 NPU 架构和编译器，这与硬件/算法协同设计方法（例如 [21]、[22]）不同，也不同于仅定制可编程/可重构处理器而不进行编译器定制的方法（例如 [23]、[24]）。总之，现有的硬件加速器生成器在支持较新的网络模型方面相当不灵活，且无法支持先进的 BNNs。

另一方面，尽管通用处理器的编译器足够灵活，可以支持任何 BNNs，包括先进的 BNNs，但由于指令级并行度有限，通常无法提供足够的性能和加速效果。本文的方法通过扩展现有的 NPU 架构和编译器框架，可以在保持灵活性以支持多种网络模型的同时，提供更实质性的加速。

3. 扩展多功能张量加速器

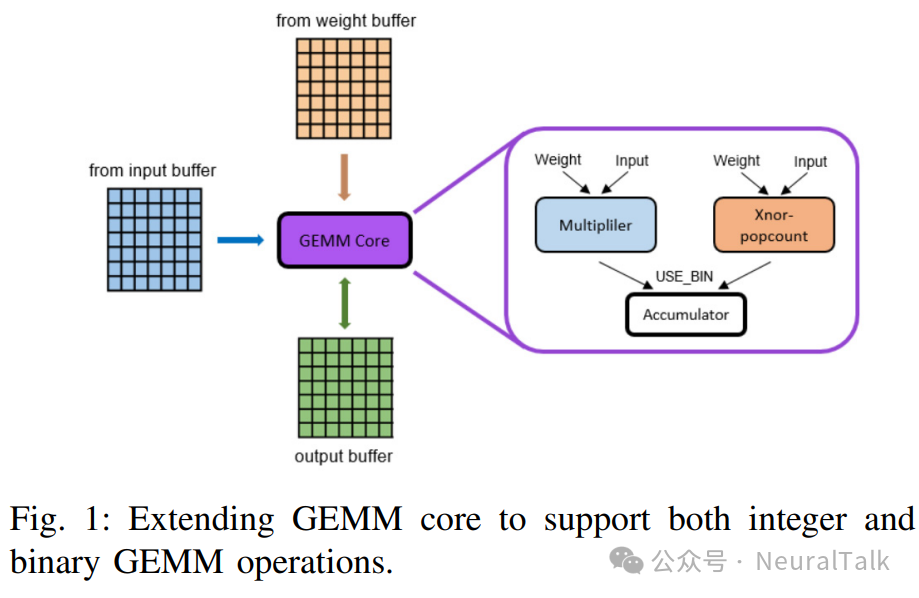
多功能张量加速器（VTA）[10] 是一种开源的可编程神经处理单元（NPU）架构，具有四个 128 位指令：加载、存储、GEMM、ALU。GEMM 对于性能最为重要，执行实际的卷积和全连接层操作。我们通过新增一个 1 位字段来扩展 GEMM 指令，使其能够执行整数或二值 GEMM 操作。

这里存在两个问题：如何添加新功能，以及如何利用新功能。

A. 添加新核心与添加新功能单元

我们研究了两种实现二值 GEMM 功能的方法。

一种方法是在原有 GEMM 核心旁添加一个额外的 GEMM 核心，这更为直接。然而，尽管两个核心可以同时运行，但它们共享相同的输入/输出缓冲区，这意味着在任何时间只有一个核心能够执行有用的计算。

因此，一种更具成本效益的方法是在 GEMM 核心中添加一个用于二值 GEMM 操作的新功能单元（FU），如下图 1 所示。我们在第 VI-B 节比较了这两种方法的成本。

B. 程序员对扩展 GEMM 的视角

无论执行整数还是二值 GEMM，GEMM 核心的输入/权重/输出数据都具有完全相同的数据大小。这有两个含义。首先，虽然整数 GEMM 执行的是 int8 数据类型的（16, 16）矩阵与（16, 1）向量的乘积，但新的二值 GEMM 执行的是 8 位字长下的（16, 16, 8）张量与（16, 1, 8）张量的 1 位数据类型的乘积。其次，输出大小相同意味着在二值 GEMM 情况下，额外的大小为 8 的维度必须用于输入通道。

换句话说，我们把二值 GEMM 情况下的权重和输入张量解释（或 reshape）为具有（16, 128）和（128, 1）的形状。这种观点的一个缺点是，如果二值化层的输入通道少于 128 个，二值 GEMM 核心将只能被部分利用。算法 1 展示了图 1 中作为新功能单元实现的扩展 GEMM 的伪代码。

4. 扩展编译器

我们的编译器基于 Glow 构建，同样以 ONNX 作为输入，并生成支持我们扩展 VTA 的代码，该 VTA 支持各种 DNN（包括 BNN）。我们对编译器的设计目标是在支持最近的 BNN 模型的同时，不破坏工具或输入格式的兼容性。

为了支持 BNN，我们必须回答以下问题：

（i）支持 BNN 需要哪些额外的操作
（ii）如何识别二值化层

此外，我们还将在第 V 节讨论编译器优化，以最大化 BNN 的性能。

A. 初步：Glow 编译框架

我们首先简要回顾 Glow 框架 [18]，我们的工作就是基于它进行扩展的。Glow 是一个开源的机器学习（ML）编译框架和执行引擎，旨在作为 DNN 框架（例如 Tensorﬂow、PyTorch）的后端使用。Glow通过两阶段的中间表示（IRs）将 DNN 框架生成的模型转换为机器代码。

高级 IR是一个基于节点的计算图，它直接将 DNN 框架操作转换为一个或多个节点。可以在高级 IR 上执行与目标无关的优化，例如操作融合。之后，Glow 将高级 IR 降低为低级 IR。
低级 IR是一个基于指令的 IR，它允许基于目标的优化和与内存相关的优化。

之后，Glow 执行适合其硬件特征的特定于硬件的代码生成。

B. 所需额外操作

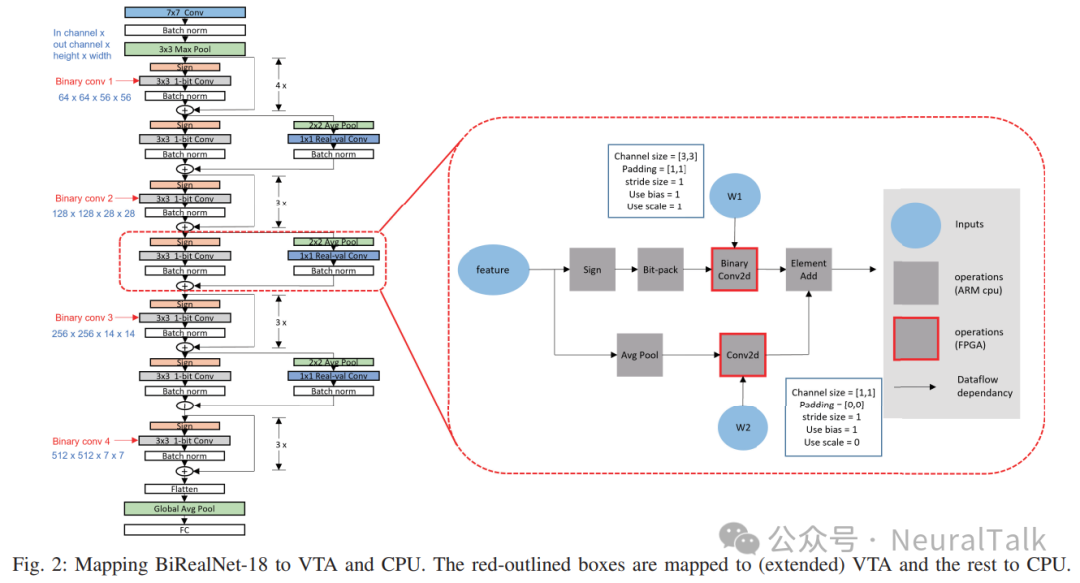
下图 2 展示了 BNN 的计算图是如何映射到我们扩展的 NPU 的。除了二值化操作本身（例如二值卷积），其输入操作数（输入激活和权重）首先必须被二值化和位打包。通常使用符号函数进行二值化，但符号函数的结果通常作为整数数组存储在内存中，每个数组元素要么是 1 要么是 −1。

二值 GEMM 核心期望输入是位向量，因此有必要将整数数组转换为位向量，这被称为位打包。输入激活的二值化和位打包必须在运行时完成，我们在 CPU 上的软件中完成这一操作。另一方面，二值化计算的输出是一个整数数组，不需要特殊处理。

C. 实现问题：识别二值化层

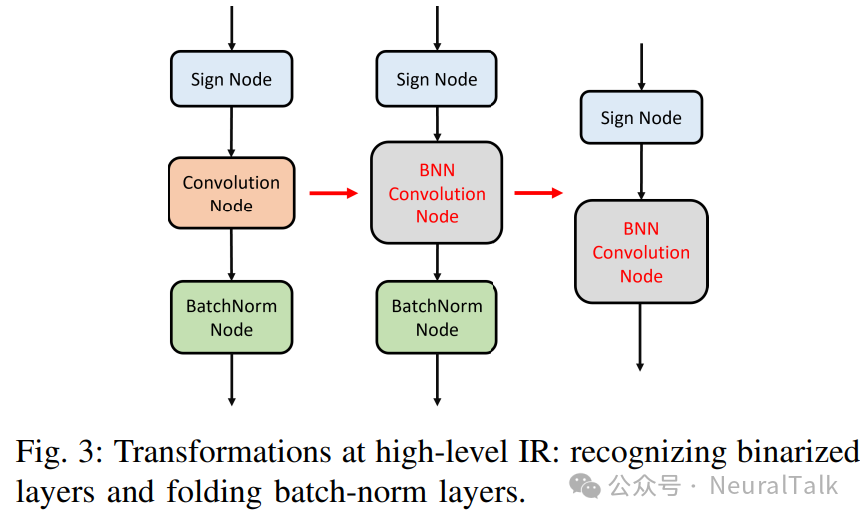
在扩展编译器以支持 BNN 时的一个问题是，在 DNN 框架中通常没有专门的二值卷积 / 全连接层操作符，这使得在编译器的前端识别二值化层变得具有挑战性。虽然我们可以引入新的二值化层操作符，但它们将不会被其他编译器 / 工具链所识别，从而破坏互操作性。

相反，我们观察到在二值化层之前的输入激活处通常会放置一个符号函数，我们将这样的层解释为二值化层，如图 3 所示。我们的方法不需要对 ONNX 格式进行任何更改。在创建二值化计算节点时，我们还添加了一个名为缩放因子的参数，该参数可以是按通道的，用于存储与二值化相关的缩放因子（s）。

5. 编译器优化

A. 用于带残差连接的二值化层的批归一化折叠

批归一化（BN）层在卷积层之后使用非常频繁。对于推理，BN 层的参数是固定的，因此可以简化为一个仿射变换。因此，卷积层和紧随其后的仿射层可以合并为一个单独的卷积层，这就是所谓的 BN 折叠 [1]。

然而，现有的 BN 折叠方法要么（i）改变前一层卷积层的权重和偏置[1]，这在权重精度足够时有效，要么（ii）在 BNNs 中，仅改变偏置[20]，基于 BN 层输出立即被二值化（即后面跟着符号函数）的假设。然而，存在第三种情况：BN 层跟在二值卷积层之后但没有紧跟着符号函数，如图 2 所示。

在这种情况下，没有现有方法可以工作，但幸运的是，我们仍然可以通过使用二值卷积相关的缩放因子来折叠 BN 层。以下是我们在带有残差连接的二值化层中进行 BN 折叠的方法，该方法将 BN 参数不是折叠到权重和偏置中，而是折叠到缩放因子和偏置中。

其中 Wb 是二值化权重，α 是按通道的缩放因子。BN 层的输出 z：

将上述方程联立得出：

因此，经过 BN 折叠后二值化层的新缩放因子和偏置如下。

B. 映射少输入通道（FIC）卷积

图像处理 CNNs 中的第一卷积层通常输入通道数非常少，例如 3 个。由于我们将 GEMM 核心的两个维度映射到输入和输出通道维度，因此如果通道数少于 GEMM 硬件维度（在我们的情况下为 16×16），则无法充分利用 GEMM 核心的全部计算能力。例如，使用仅 3 个输入通道会浪费大约 81%（= 1 − 3/16）的计算能力。

为了解决 FIC 卷积（如第一卷积层）的低利用率问题，我们将卷积转换为 1x1 卷积。例如，BiRealNet-18 的第一卷积层的权重维度为（64, 3, 7, 7）=（输出通道，输入通道，内核大小 y，内核大小 x），输入激活的维度为（1, 3, 224, 224）=（批量大小，输入通道，高度，宽度）。

注意步幅为 2。如果直接将此内核映射到 VTA，如 TVM [17] 所做的那样，它只利用 GEMM 核心的（16, 3）子数组，被调用 4 × 7 × 7 = 196 次。相反，我们将权重张量重塑为（64, 3 · 7 · 7, 1, 1）=（64, 147, 1, 1），这将调用（16, 16）GEMM 操作 4 × 10 = 40 次，实现 GEMM 核心利用率提高 4.9 倍。然而，我们方法的缺点是输入张量必须重新排列为（1, 147, 112, 112），类似于 img2col（112 = 224/2，由于步幅），重复大量数据，这可能会在一定程度上抵消性能提升。

此外，输入激活必须在运行时由 CPU 重新排列，增加了开销。根据我们的硬件测量结果，我们的 FIC 卷积映射优化在 BiRealNet-18 的第一卷积层上实现了 3.44× 的加速，如表 I 所示（请参阅第 VI-A 节了解我们的实验设置）。

C. 任务级流水线并行

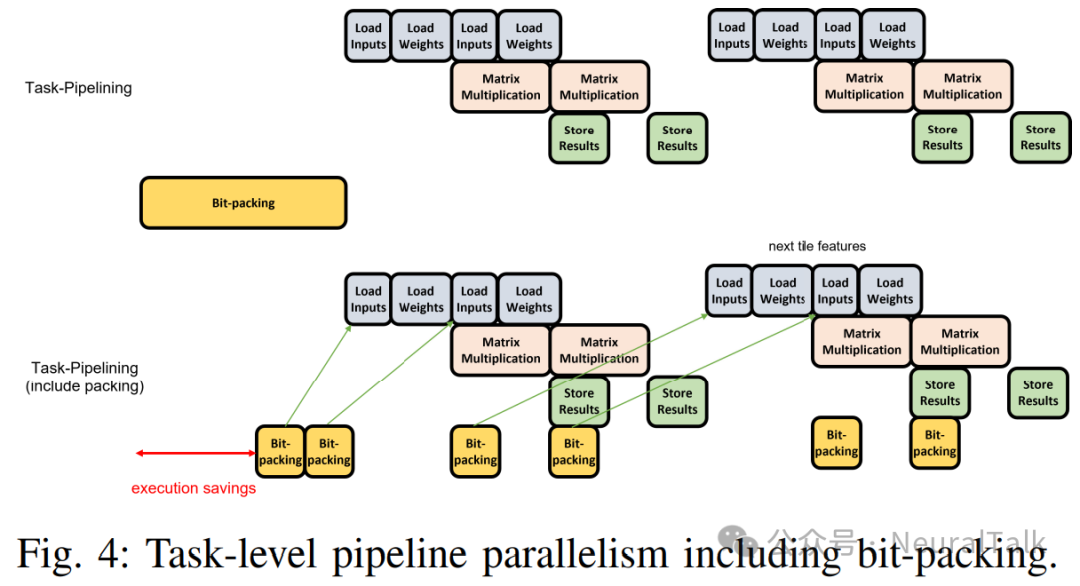
VTA 在加载、GEMM 和存储指令之间实现了任务级流水线并行（TLPP）。在我们的情况下，我们还有一个额外的任务，即位打包，也可以进行流水线处理。

图 4 描述了将位打包包含在 TLPP 中的想法。一个区别是位打包是在 CPU 上运行的软件任务，而不是 GEMM 指令。通过将位打包与 GEMM 操作进行流水线处理，我们可以期望部分隐藏位打包的延迟，从而提高吞吐量。

6. 实验

A. 实验设置

为了评估我们的框架和加速器，我们使用了 BiRealNet-18[7]，这是ResNet-18 的二值化版本，用于 ImageNet 分类。我们已经在Xilinx ZCU102 FPGA 板上实现了我们的扩展 VTA，以及从 Glow 扩展而来的编译器。我们使用 BiRealNet-18 验证了我们编译器和扩展 VTA 的正确操作。

本文报告的所有性能数据都是在 FPGA 板上实际测量得出的。ZCU102 FPGA 板包含一个 Zynq UltraScale+ 设备，其中包括一个 ARM Cortex-A53 CPU。只有卷积、二值卷积和全连接层被映射到 FPGA，而其他层被映射到 ARM CPU（请参阅图 2）。对于 VTA，GEMM 核心被配置为 16×16，精度为 8 位。偏置加法为 32 位。

B. FPGA 资源利用率

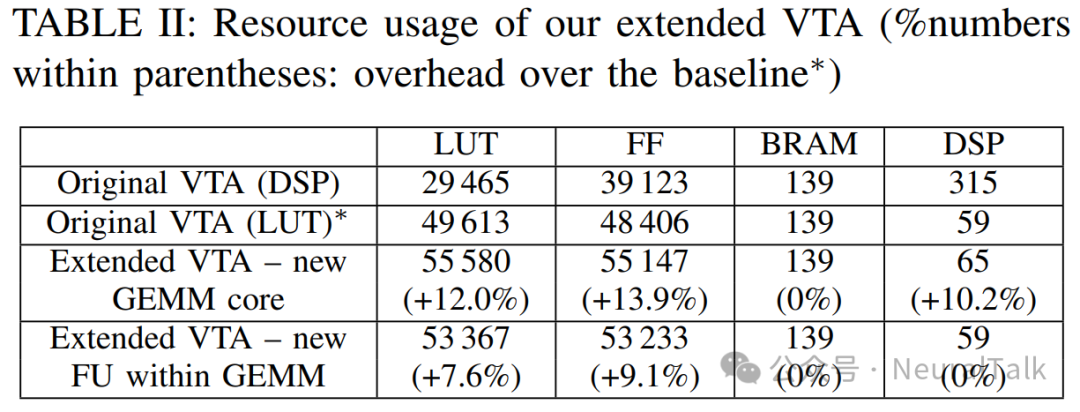
表 II 比较了我们在 ZCU102 上实现的扩展 VTA 的 FPGA 资源利用率。时钟频率设置为 333 MHz，与原始 VTA 相同。

原始 VTA 以两种不同的方式实现。以 LUT 版本为基线，我们比较了我们的扩展 VTA 实现。即使采用新 GEMM 核心方法，面积开销也很小，这证实了二值 GEMM 操作的硬件友好性。但采用新 FU 方法时，LUT/FF 的使用增加了 8∼9%，而更昂贵的 BRAM 和 DSP 的使用根本没有增加。我们的结果适用于 8 位，但如果我们提高精度到 16 位，我们预计我们的扩展的面积开销会更小。

C. 与 TVM-VTA 的比较

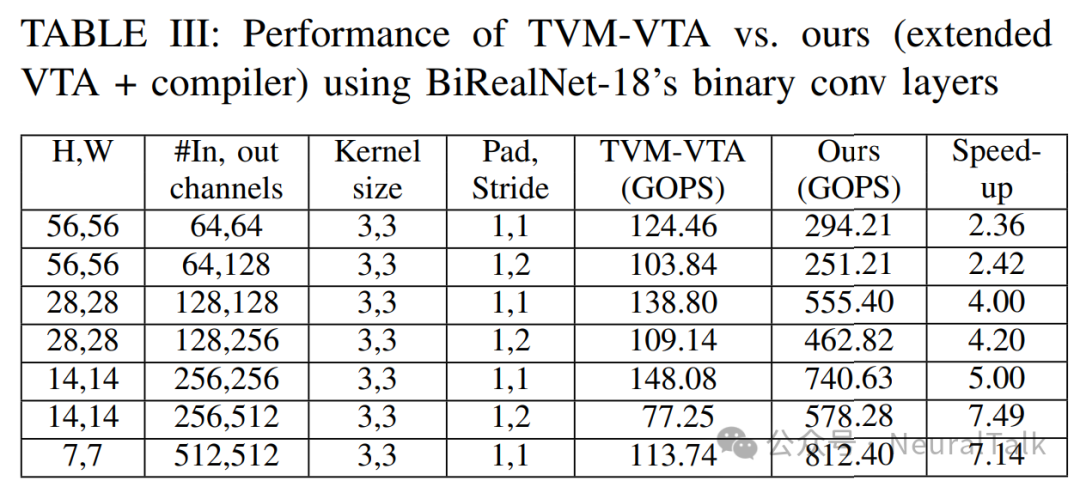
表 III 比较了 TVM 编译器在 VTA 上与我们的扩展 VTA 和编译器在 BiRealNet-18 的所有二值卷积层上的性能（图 2 中所有灰色填充的框）。

在所有情况下，VTA 的频率都设置为 333 MHz，我们的 BN 折叠优化也应用于 TVM 情况。在 TVM 情况下，二值（{−1, 1}）被表示为 int8 值，这增加了计算和内存访问的开销。在我们的情况下，我们将八个位打包到一个 int8 变量中，这意味着理想性能提升是 8×。

然而，我们有位打包的开销，这在 CPU 上运行。此外，当输入通道数少于 128 时，我们无法充分利用二值 GEMM 核心，这就是为什么表中前两层的加速效果特别低。表中最后两层，具有最多的输出通道，显示出最大的性能提升，接近理想加速。这是因为位打包的开销可以通过大量输出通道来分摊。

D. 我们编译器优化的效果

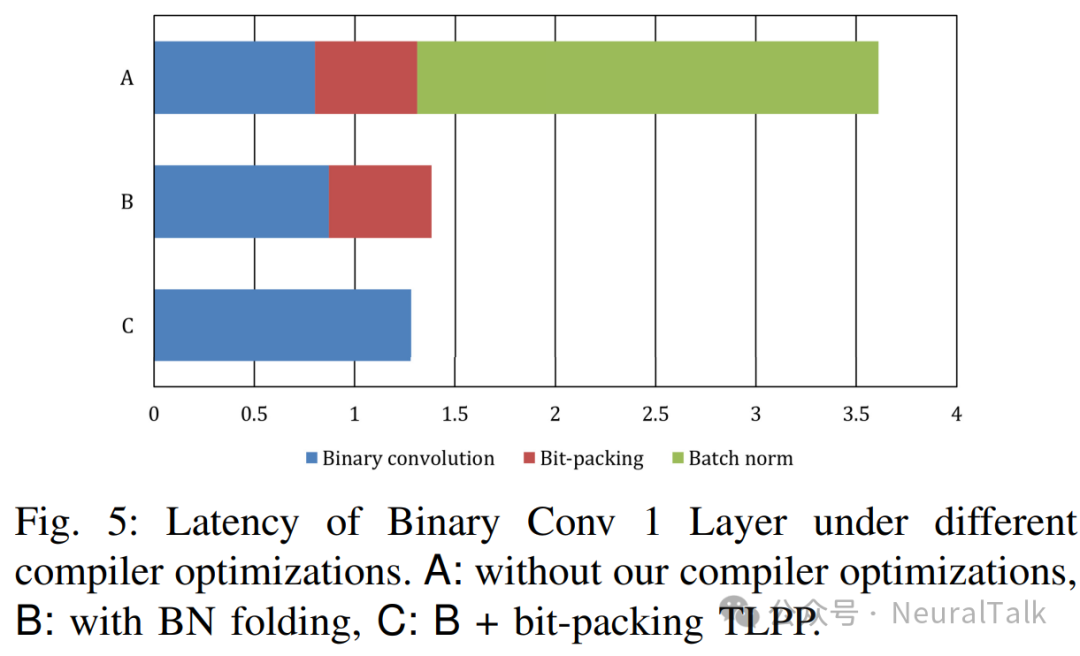
为了查看我们编译器优化的效果，图 5 比较了在不同编译器优化下二值卷积层的延迟。在这个实验中，我们使用了 BiRealNet-18 的二值卷积 1 层（请参阅图 2），这也是表 III 中的第一层。我们发现最大的性能提升来自 BN 折叠，这是因为虽然 GEMM 核心加速了卷积操作，但批归一化操作是在 ARM CPU 上的软件中执行的。

另一方面，位打包流水线与情况 B 相比，仅提供了约 10% 的适度性能提升。在流水线情况下，每次位打包向 VTA 发送 16 个 int8 变量，我们怀疑这可能由于频繁的通信开销而导致效率不高。优化通信的粒度可能会带来更好的性能，这留待未来工作。

E. 与 BNN 编译器的比较

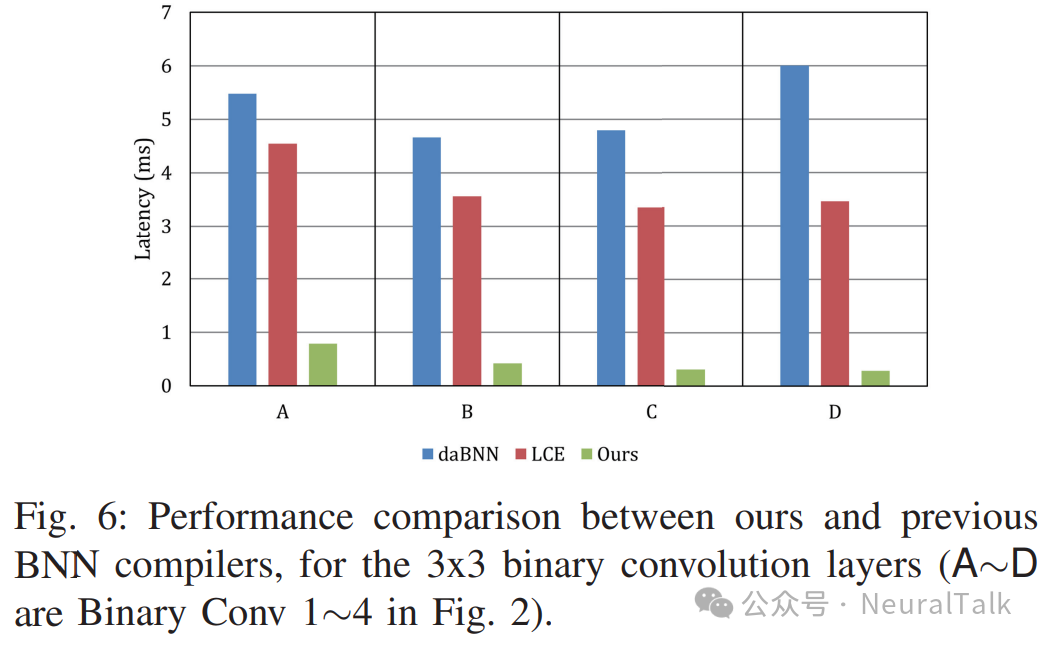
除了与 TVM 的比较外，我们还将我们的方法与最新的 BNN 编译器方法（如 daBNN 和 LCE）进行了比较。图 6 显示了 BiRealNet-18 的二值卷积层的延迟。注意，BNN 编译器方法使用 ARM Cortex-A53，这与我们的情况相同，但我们的案例还额外使用了 GEMM 核心。虽然 LCE 在两者中通常提供更好的性能，但我们的 NPU 案例在 LCE 情况下额外提供了 6∼12× 的加速，这证实了我们方法的有效性。

7. 结论

现代二值化神经网络（BNNs）在性能上极具竞争力，且更加硬件友好。然而，为了在 NPU 硬件上充分利用 BNN 模型的硬件友好位运算，我们需要扩展 NPU 架构以及编译器 。

本文的创新思想包括：

针对具有缩放因子且未立即跟符号函数的二值化层 的批归一化折叠方法 ，在这种情况下，以前的方法无法应用；
对输入通道较少的卷积 进行高效处理；
位打包流水线 。

我们使用 BiRealNet-18 进行的评估表明，我们的编译器 - 架构混合方法可以在二值卷积层上相较于基线 VTA 实现显著的速度提升 ，特别是在输出通道较多且输入通道数为 128 的倍数时 。

此外，我们的方法在 BiRealNet-18 的端到端性能上相较于 BNN 编译器方法有显著提升 。在未来，我们计划考虑更高效的位打包处理方法 ，例如使用硬件以及 CPU 和 NPU 之间更优化的数据传输方案。

参考文献

[1] R. Krishnamoorthi, “Quantizing deep convolutional networks for efficient inference: A whitepaper,” arXiv preprint arXiv:1806.08342, 2018.
[2] S. K. Esser et al., “Learned step size quantization,” arXiv preprint arXiv:1902.08153, 2019.
[3] S. Oh et al., “Automated log-scale quantization for low-cost deep neural networks,” in Conference on Computer Vision and Pattern Recognition (CVPR), Jun. 2021, pp. 742–751.
[4] F. Asim et al., “Centered symmetric quantization for hardware-efficient low-bit neural networks,” in British Machine Vision Conference (BMVC), Nov. 2022.
[5] S. Oh et al., “Non-uniform step size quantization for accurate post-training quantization,” in European Conference on Computer Vision (ECCV), Oct. 2022.
[6] Z. Liu et al., “ReActNet: Towards precise binary neural network with generalized activation functions,” in European conference on computer vision. Springer, 2020, pp. 143–159.
[7] ——, “Bi-real net: Enhancing the performance of 1-bit cnns with improved representational capability and advanced training algorithm,” in Proceedings of the European conference on computer vision (ECCV), 2018, pp. 722–737.
[8] Y. Umuroglu et al., “Finn: A framework for fast, scalable binarized neural network inference,” in FPGA, 2017, pp. 65–74.
[9] S. Liang et al., “Fp-bnn,” Neurocomput., vol. 275, no. C, p. 1072–1086, jan 2018.
[10] T. Moreau et al., “A hardware-software blueprint for flexible deep learning specialization,” IEEE Micro, vol. 39, no. 5, pp. 8–16, 2019.
[11] I. Hubara et al., “Binarized neural networks,” Advances in neural information processing systems, vol. 29, 2016.
[12] M. Rastegari et al., “XNOR-net: Imagenet classification using binary convolutional neural networks,” in European conference on computer vision. Springer, 2016, pp. 525–542.
[13] J. Bethge et al., “Bmxnet 2: An open source framework for low-bit networks-reproducing, understanding, designing and showcasing,” in Proceedings of the 28th ACM International Conference on Multimedia, 2020, pp. 4469–4472.
[14] J. Zhang et al., “dabnn: A super fast inference framework for binary neural networks on arm devices,” in Proceedings of the 27th ACM international conference on multimedia, 2019, pp. 2272–2275.
[15] J. Fromm et al., “Riptide: Fast end-to-end binarized neural networks,” Proceedings of Machine Learning and Systems, vol. 2, pp. 379–389, 2020.
[16] L. Geiger and P. Team, “Larq: An open-source library for training binarized neural networks,” Journal of Open Source Software, vol. 5, no. 45, p. 1746, 2020.
[17] T. Chen et al., “TVM: An automated end-to-end optimizing compiler for deep learning,” in 13th USENIX Symposium on Operating Systems Design and Implementation (OSDI 18), 2018, pp. 578–594.
[18] N. Rotem et al., “Glow: Graph lowering compiler techniques for neural networks,” arXiv preprint arXiv:1805.00907, 2018.
[19] A. Azamat et al., “Squeezing accumulators in binary neural networks for extremely resource-constrained applications,” in International Conference on Computer-Aided Design (ICCAD), Oct. 2022.
[20] S. Lee et al., “Architecture-accuracy co-optimization of ReRAM-based low-cost neural network processor,” in the 30th ACM Great Lakes Symposium on VLSI (GLSVLSI), Sep. 2020, pp. 427–432.
[21] J. Choi et al., “MLogNet: A logarithmic quantization-based accelerator for depthwise separable convolution,” vol. 41, no. 12, pp. 5220–5231, Dec. 2022.
[22] S. Lee et al., “Successive log quantization for cost-efficient neural networks using stochastic computing,” in the 56th Annual ACM/IEEE Design Automation Conference (DAC), Jun. 2019, pp. 7:1–7:6.
[23] J. Lee and J. Lee, “NP-CGRA: Extending CGRAs for efficient processing of light-weight deep neural networks,” in Design, Automation and Test in Europe (DATE), Feb. 2021, pp. 1408–1413.
[24] ——, “Specializing CGRAs for light-weight convolutional neural networks,” vol. 41, no. 10, pp. 3387–3399, Oct. 2022.

END

作者：UNIST
来源：NeuralTalk

推荐阅读

欢迎大家点赞留言，更多 Arm 技术文章动态请关注极术社区嵌入式AI专栏欢迎添加极术小姐姐微信（id:aijishu20)加入技术交流群，请备注研究方向。