本文是本系列第五篇,本文书接上文,来讨论如何具体地针对 SM3 算法的特点,优化计算架构,如通过 CSA 加法器来优化加法关键路径等方法,提升系统频率,提高系统吞吐性能。
首发知乎
作者:李凡
SM3 中的运算
在分析关键关键路径之前,首先分析 SM3 算法中涉及的运算。SM3 运算量集中在消息压缩模块中。从下图中的运算列表可以发现,主要的运算包括:循环移位(<<< 表示循环移位),异或以及加法。
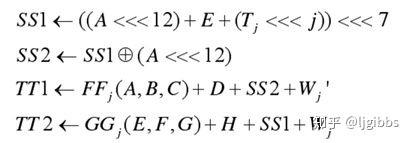
所有运算中,循环移位运算开销最小,在硬件上实现为两级触发器间的交换连线位置。
reg [2:0] A; reg [2:0] B;
B <= { A[1:0] , A[2] };
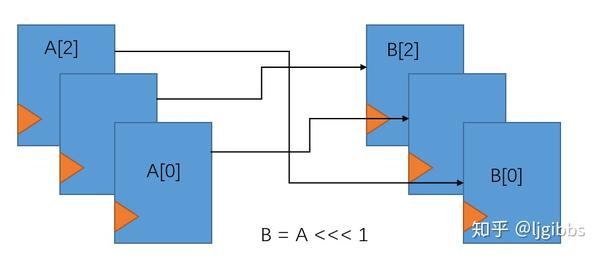
循环移位实现示意
异或运算通过 LUT 布尔函数实现,开销小且固定,具体速度与使用的器件等级相关。以 Xilinx 的架构为例,UltraScale+ 器件的 LUT 延迟比 7 系列器件低一半以上。下图为一个双输入 LUT,实现异或运算的真值表。
加法运算的时间开销最大,加法运算可以划分为全加运算和进位。加法器中每一位都是一个全加器( Full Adder )。全加器本质上还是一个布尔逻辑运算,分别计算和 S 以及进位 C,在 FPGA 中照例是映射在 LUT 上实现,开销小且固定。
S = (A ^ B) ^ X
C = (A ^ B)X + XY = AB + AX + AY
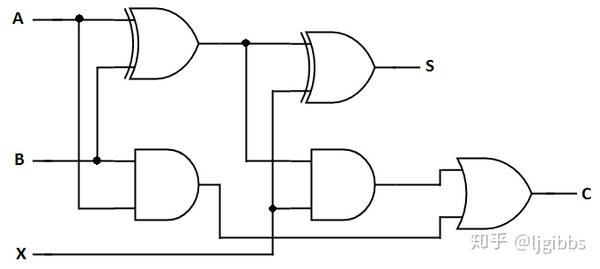
全加器
加法器的主要延迟在于从最低位开始,直至最高位的逐位进位逻辑。以普通的行波进位加法器 ( Ripple Carry Adder) 为例,下图是一个4bit 行波进位器:
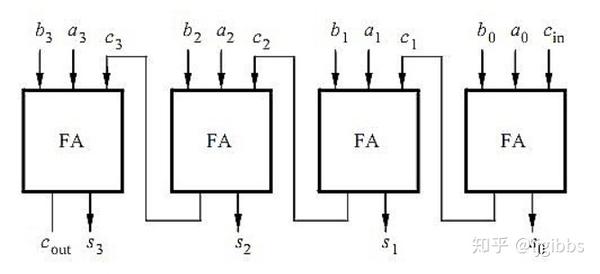
4 位加法器
运算结果 S 输出需要等待从输入进位 Cin 开始直到进位到 C3 ,经过 3 个全加器这么长的路径后,才可以到最后一个全加器进行最后一次加法运算后输出,关键路径为从 Cin 经过 4 个全加器到达 Cout 。我们可以得到此次加法运算的延迟:
Tdelay = 4 * Tcarry + Tsum ≈ N * Tcarry (N 位加法器)
进位延迟 N * Tcarry 和加法器位宽成正比,而几乎与全加运算延迟 Tsum 无关。为了优化通用加法运算中进位的延迟,FPGA 在内部结构中设计了一种专用结构:进位链( Carry Chain ) ,通过预先搭好的 CMOS 电路,而不是可编程的 LUT,实现更快速,低延迟的进位。从而提升加法运算的速度。
想了解更多有关进位链的知识,可以参照下方这篇文章,讲得很好。
https://zhuanlan.zhihu.com/p/64764933
SM3 运算的关键路径
回到 SM3 的压缩函数的关键路径,从运算规则上可以发现到寄存器 E 的运算最为复杂,那么一般来说其关键路径也极有可能最长。
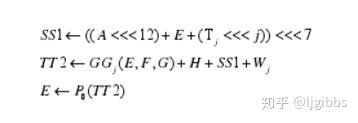
在计算中间变量 TT2 时,从表达式上看共有两级 32 位加法器,6 个数值参与。第一级加法器的运算结果为中间变量 SS1,SS1 经过循环移位后作为加数参与计算 TT2 的第二级加法运算。
在软件实现中,我们首先计算 SS1 ,然后将 SS1 循环移位,最后再和其他数相加得到 TT2,所以计算 TT2 的过程是一个两级加法器运算。
但我们考虑一个问题,硬件实现中我们是否需要做两级加法运算?综合器又是如何具体通过加法器来实现这些超过两个加数的加法运算?基本加法器可以认为是两输入的。
中间变量经过 P0 函数得到寄存器值 E,P0 是一个移位异或函数,总之在硬件上表现为一个组合逻辑,通过一级 LUT 实现。同理,运算中的 GGj 函数也用一级 LUT 实现组合逻辑。
本文我们仍将继续上篇文章中解析的开源实现来分析时序。
https://zhuanlan.zhihu.com/p/89487611
将原版的,未经优化的设计综合。时序报告和先前分析一致,关键路径确实为到达寄存器 E 的路径。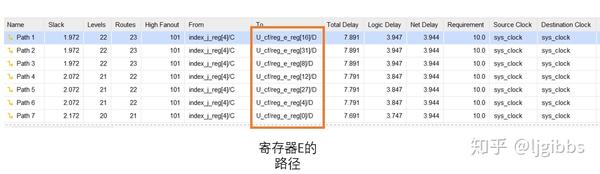
路径的开始与结束
关键路径以迭代轮次 index 寄存器作为起点。迭代 index 寄存器在顶层,以状态机的形式控制迭代的进行,当 index 自增时,新一轮迭代开始。所以我们迭代生成寄存器 E 值的路径也就从此开始。
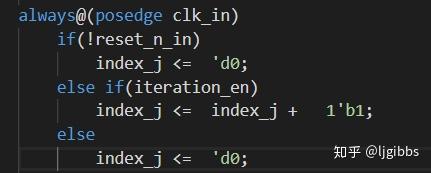
迭代使能期间,每个周期进行一次迭代,index 也每周期递增 1
路径结束与寄存器 E 锁存当前迭代轮的结果。当本轮迭代周期结束,寄存器 reg\_e 锁存本轮的迭代结果 tt2\_after\_p0 ,并作为下一轮迭代的起始值。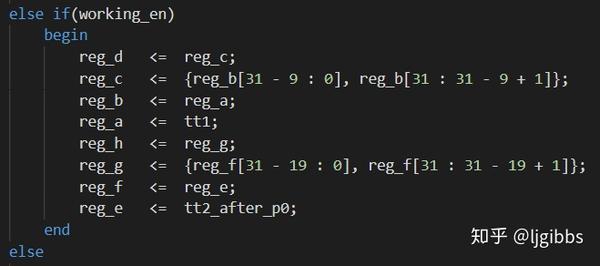
关键路径的长度决定了系统的工作频率。系统的工作周期不能太小,以至于当迭代结果还未算出时,当前工作周期已经结束。寄存器 reg\_e 锁存到的将不是正确的迭代结果,而是迭代的中间值,结果错误。
当前关键路径的长度小于 8ns ,那么可以将系统工作频率设为 125 Mhz (周期 8ns )。为了提高系统频率,就需要进一步缩短关键路径。
设想的道路

上图是根据计算规则设想的路径,通过分析路径上每个步骤的延迟发现,Tj 移位逻辑的延迟达到 2.5ns ,占到总延迟的 25 % 。实现中通过一个移位数量可配置的循环移位模块,来实现 Tj 在每个迭代周期中的循环移位,移位位数通过输入端口 shift\_number\_in 配置:
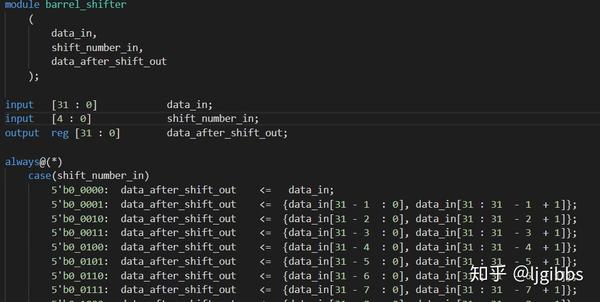
可配置循环移位模块
常量 Tj 参与到迭代中,并在每轮迭代中需要进行一次循环移位,比如在第 n 轮迭代时,参与迭代的常量是 Tj <<< n。原作者通过上述的移位模块实现常量的更新,使用当前迭代轮的 index 控制移位位数,用于产生 Tj <<< index 。这也就是为什么 index 会参与到路径中的原因。
考虑到移位逻辑占据的路径过长,并且我们总共只有 64 轮迭代,可以穷举 Tj 所有的移位情况写入一个 ROM 中,共使用 64x32b 空间,迭代中使用 index 作为地址,从 ROM 中寻址,使用查表法替代循环移位。ROM 的扇出不小,所以输出端再添加一个 output register 来进一步改善时序,在开销比较小的情况下,通过面积换时间策略往往能取得很好的效益。
这里推荐来自 xilinx 工程师有关时序优化的知乎文章,可以参阅其中优化 BRAM 输出时序的部分
https://zhuanlan.zhihu.com/p/89829776
查表法优化后的路径
重新综合后,关键路径的时序得到改善, 时序裕度 slack 增加到 2.68 。

查表法优化后的关键路径
通过使用查表法,将关键路径的延迟从 7.89 降低到 7.18, 获得了 9% 的性能提升。付出的代价是面积,使用 0.5 个 BRAM 块用作 ROM。虽然使用的空间远小于 0.5 个 9K BRAM 块,但 BRAM 最小单位为 0.5。
此时综合器得到的关键路径如下图所示。
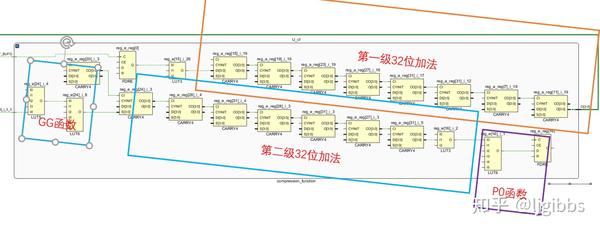
图中有两级由 8 个 4bit Carry 进位链组成的 32 位加法器,以及一些 LUT 用于进行 GG,P0 等组合逻辑函数实现。由于 Carry 使用的是专门的进位电路,所以延迟极小。
此时的延迟 T = 2 * Tadder + Tcmob ,等于两级加法器的延迟加组合逻辑的延迟。综合器在分析了我们的 RTL 代码后,认为需要首先算出中间变量 TT1,对 TT1 移位后再计算 TT2。
组合逻辑的延迟基本不变,本文优化的重点就在于降低加法带来的延迟,尤其是延迟的主要原因——加法逐位进位。
使用 CSA 优化加法路径
在优化加法器之前,我们首先分析一下 SM3 中加法计算的特点:
32 位无符号数加法 加法运算的的加数和运算和均为 32 位无符号数。
丢弃进位 当产生进位时,直接丢弃进位。
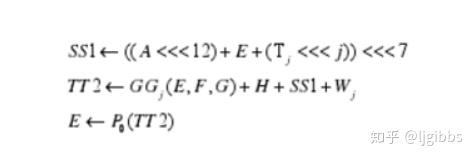
在 E 的生成路径上的加法有以下特点:
- 有 6 个参与运算的加数
- 中间变量 SS1 循环移位后参与 TT2 的加法运算
如果按照未经优化的二输入加法树,整个运算路径会长这个样子: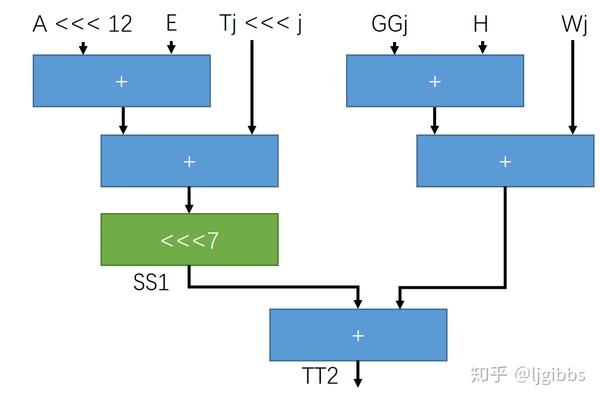
运算分为左右两路加法进行,此时延迟为 T = 3*Tadder + Tshift
加法器延迟包括位加法运算延迟和逐位进位延迟,逐位进位通过 Carry 进位链实现,加法运算延迟主要为逐位进位延迟。
通过上图可以观察到,最后一级加法器需要通过逐位进位运算计算出结果 TT2,而之前的两级加法器运算得到的实际上是中间变量,并不一定需要逐位进位,而只要分别保留加法的 和 & 进位 到最后一级加法再将 和 & 进位相加即可。
因此,我们在前级的加法器中引入进位保留加法器 Carry Save Adder, CSA.
CSA 其人
CSA 的原理是在计算 X+Y+Z 时,分别计算加法和 S 以及进位 C 输出,这两者都通过组合逻辑产生。
S = X ^ Y ^ Z
C = (X & Y) | (X & Z) | (Z & Y)
CSA 输出时不进行逐位进位计算,故 CSA 的延迟很低。S + C 的进位计算保留到后级执行,故名进位保留加法器。 后级运算时再将 S 和 C 进行逐位进位的加法运算。
SUM = S + (C << 1)

CSA 示意图
当需要进行多级加法器运算,并且多级运算期间可以保留进位时,使用 CSA 可以节约 (N-1)*Tcarry 延迟,其中 N 为加法器级数。
CSA 优化
使用 CSA 优化我们的加法树后,减少了一级加法器延迟。但我们遇到一个问题,如果不对循环移位运算进行处理,我们仍然需要先计算出中间变量 SS1,还是需要两级加法进位延。
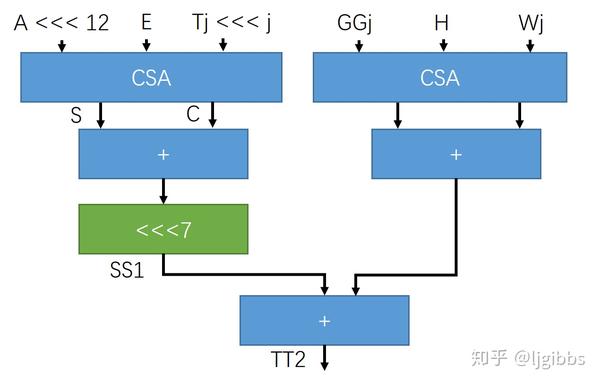
这里是两级延迟,综合结果也是两级加法器延迟,觉得很巧有木有?>\_< 实际上,综合自动执行了这步 CSA 优化,将第一级 CPA 优化成了 CSA。CPA 指的是普通的加法器,进位传播加法器 Carry propagate。
综合器会在通用的情况下,对多输入加法会自动进行 CSA 优化。但在特定的,比较复杂的情况下,比如此时涉及到加法之后做移位运算的情况,综合器可能就选择多一事不如少一事,放弃进一步的优化。
CSA 再优化
既然循环移位运算挡在我们之前,那我们就把他干掉....对他做一点调整。我们可以对循环移位之前的 CSA 结果进行移位调整,也就是对 S 和 C 循环移位,再将移位后的结果和其余加数相加,就是这样:
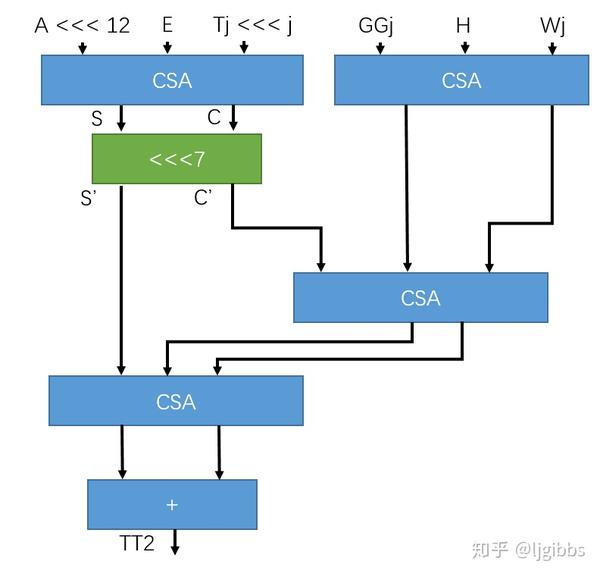
这样一来,整体延迟下降到 3*Tcsa + Tshift + Tadder ,由于 CSA 与移位运算的延迟较小,所以系统的整体延迟下降。
超前循环移位的进位修正
但这样循环移位存在一个进位补偿问题,因为实际上没有计算 SS1,
原本为 SS1 <<< 7 (S + C) <<< 7
现在替代为 S <<< 7 + C <<< 7
但替代过程中没有考虑 S + C 的进位情况就进行了移位,
SS1 => {SS1 [24:0],SS1 [31:25]}
会导致移位部分 SS1 [31:25] 的向前进位错误地进位到 SS1 [24:0],SS1 [24] 的向前进位会被直接丢弃,而不是进位到 SS1 [31:25]。
所以需要在 CSA 计算的同时,使用逐位进位加法器计算出 SS1 的值,产生 SS1[31],SS1[24] 的向前进位信号,对最终的结果 TT2 进行进位修正。修正值使用额外的加法逻辑并行产生。
修正结构如下:
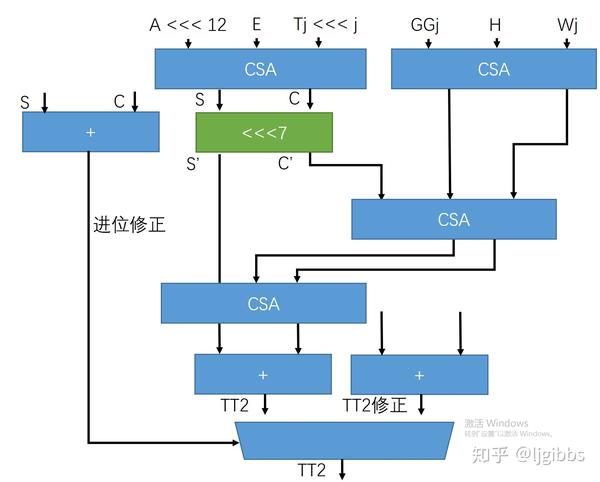
所以最终增加了一个选择器的延迟 T = 3*Tcsa + Tshift + Tadder + Tmux
如图是综合得到的网表

可以看到此时关键路径上只剩下 1 级加法器的进位链。
寄存器 E 的最长路径只剩下 6.034 ns
 不过此时的最长路径变成了寄存器 A 的路径,延迟 6.72 ns,所以系统的最高频率现在受限于寄存器 A 值的生成。
不过此时的最长路径变成了寄存器 A 的路径,延迟 6.72 ns,所以系统的最高频率现在受限于寄存器 A 值的生成。
 A 的路径应当也是可以以类似的方法被优化的,我们将在后续的文章中讨论。
A 的路径应当也是可以以类似的方法被优化的,我们将在后续的文章中讨论。
结语
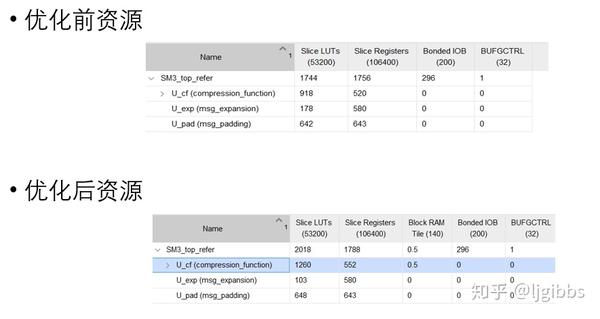
本文针对 SM3 的运算特点,进行了两项优化:查找表获取常量 以及针对 SM3 优化的加法器结构。
通过优化将延迟从 7.89 降低至 6.72, 优化了 15% 延迟。使用的 LUT 资源增加了 15%,是一次典型的空间换时间之旅。
系列篇
更多FPGA相关知识请关注我的FPGA 的逻辑专栏









