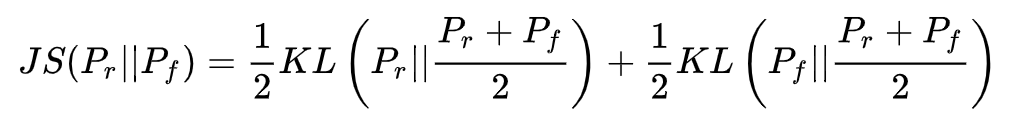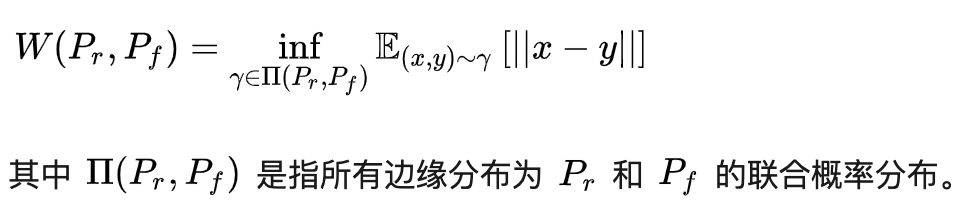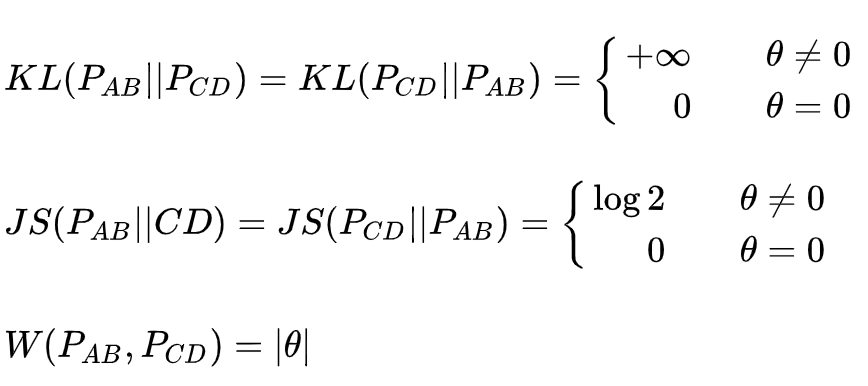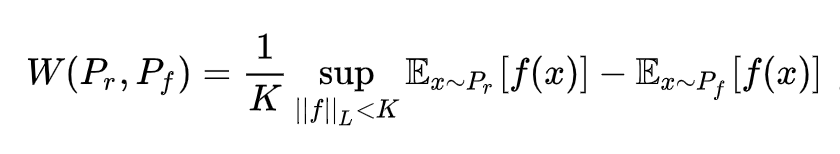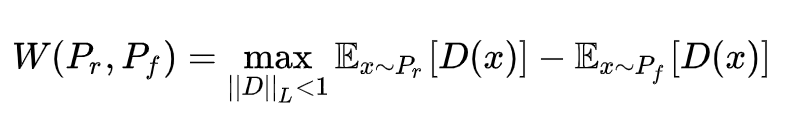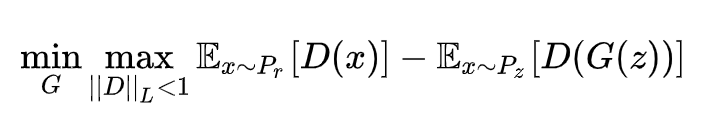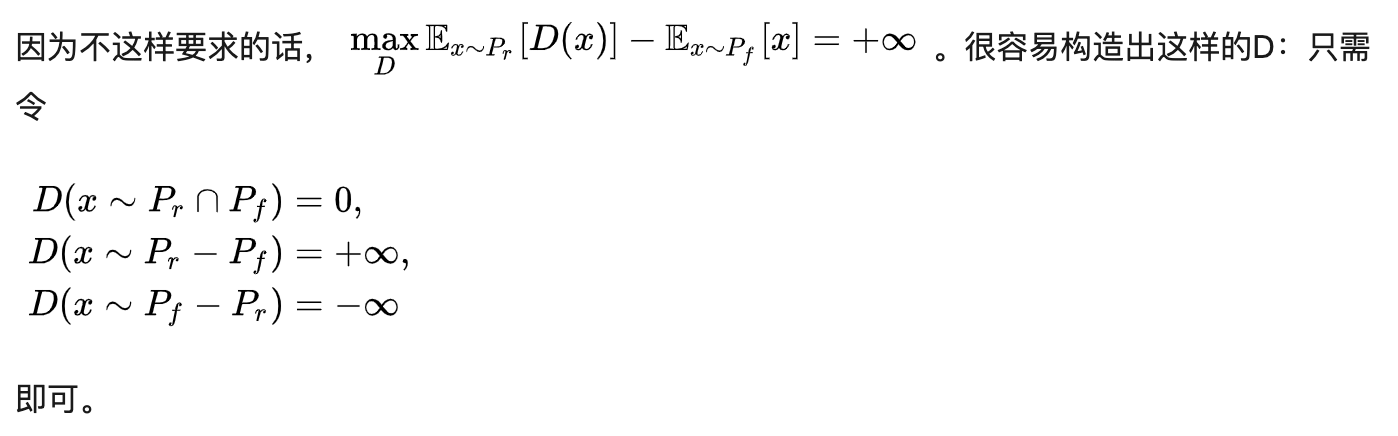GAN 论文阅读笔记!共六篇,本文为第二篇。
来源:https://zhuanlan.zhihu.com/p/56968792
作者:林小北上文《GAN论文阅读笔记1:从零推导GAN》提到,标准GAN虽然看上去很美,但是训练起来却往往难以得心应手,常常会有梯度消失的情况出现。为此,WGAN给出了非常漂亮的解释。
0. 符号定义
按照惯例,先简要介绍一下符号定义和必要的概念。
注意KL散度是不对称的,对KL散度稍加修改即可得到其对称形式,也就是JS散度(Jensen-Shannon divergence):
W距离(Wasserstein distance),俗称推土机距离(Earth-Mover distance),定义为:
这个定义比较不直观,本文将从另一个比较通俗易懂的角度去解释WGAN的形式。对于一般的读者,仅需要知道W距离跟JS散度一样都是用来描述两个概率分布的差异的一种测度即可。有兴趣深入研究的读者可以戳链接更好地理解W距离:《传说中的推土机距离基础,最优传输理论了解一下》。
Lipschitz性质:当函数f(x)满足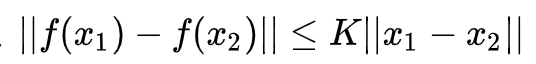
1. 原始GAN的问题
WGAN指出,《GAN论文阅读笔记1:从零推导GAN》中标准GAN的两种形式,都有问题。
此时的损失函数出现了KL散度和JS散度互相打架的情况,意见相左的两个散度将会影响整个网络的收敛。
2. W距离的优点
标准GAN的两种形式试图优化JS散度和KL散度,但这两种散度的表现不尽理想。那么,能否找到一个更加合适的测度来刻画两种概率分布的差异呢?
WGAN一文提出,W距离,正好满足我们的需求。所谓W距离,直观上理解,就是把一个分布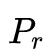
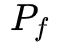
从定义上,距离是一个比散度更强的概念,需要满足对称性和三角不等式。更严格的定义带来的是更为优秀的性质,下面用一个简单的例子说明W距离的优越性:
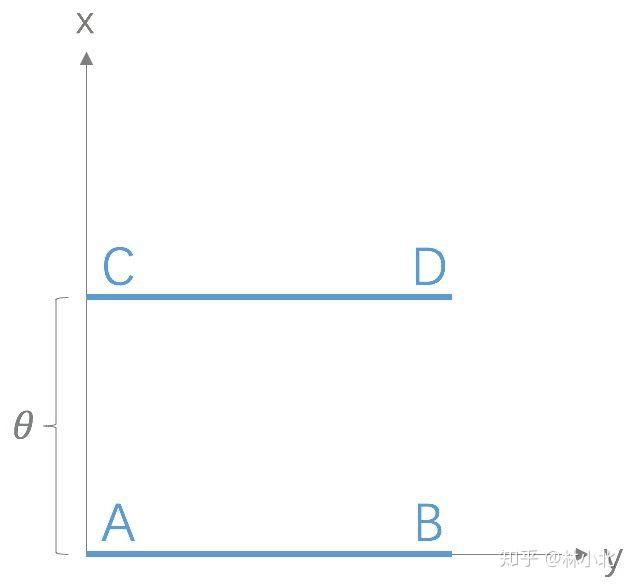
考虑如上图的两个分布,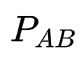
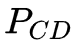
这么一对比,可以看出,W距离的优点有二:一是足够平滑;二是即便当两个分布没有交集的时候它的取值也是在变化的。此外,还有一个更为重要的优点在于:通过对GAN的判别器进行适当改造,即可得到W距离的近似。
3. 用判别器得到W距离
在标准GAN中,通过优化D来得到JS散度,再通过优化G来最小化JS散度。WGAN也是类似的思路。先通过优化D来得到W距离的近似,再通过优化G来最小化W距离。所以,WGAN的核心就在于如何改造D来得到W距离。
关于W距离,根据_Kantorovich-Rubinstein对偶性_,有这么一个酷炫的公式:
看到这个公式,叫人不禁眼前一亮!
如果我们不再局限判别器D(x)的值域为[0,1],并且令判别器D(x)满足1-Lipschitz,那么有
这样,我们就得到WGAN的表达式:
再回过头看看这两个限制条件:
(1)不再局限判别器 D(x)的值域为[0,1],也就意味着D(x)描述的不再是x为真的概率,而描述的是x为真的程度,这个操作可以通过去掉判别器最后的sigmoid层就能得到。
(2)令判别器 D(x)满足1-Lipschitz,这里WGAN的操作很简单粗暴,直接强行把D的所有参数直接clip到[-1, 1]区间,这样D(x)的每个子操作都满足1-Lipschitz,也就保证了D(x)的1-Lipschitz性质。这种处理手段显然不够优雅,为此也引发了后面WGAN-GP,SNGAN为代表的广泛讨论,这个我们回头再说。
4. 另一个角度理解WGAN
前面提到,其实不理解W距离的定义和那个酷炫的公式不要紧,可以从另一个角度去理解WGAN。
这个公式和WGAN的唯一区别在于,WGAN要求D是Lipschitz的。
那么为什么要这么要求呢?
如果不限制D的结构,那这个取值就可以是任意大的了。
所以:Lipschitz是为了保证D的优化目标有界。
5. 总结
WGAN告诉我们:
(1) D(x) 可以不刻画x为真的概率,改成刻画x为真的程度也ok,也就是说D(x)的值域没有必要是[0,1]
(2)为了保证脱掉“概率”约束的D(x)有的放矢,需要对D的函数性质进行限制。WGAN限制了D必须是Lipschitz的。
此外,总结GAN和WGAN,我们发现GAN的套路为:
(1 ) 通过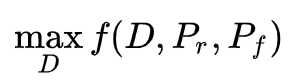
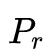
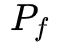
(2)通过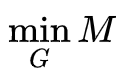
对于WGAN,我们也应该抱有这样的疑惑:
(1)是不是有更优雅的Lipschitz的手段?
(2)按照第4部分的分析,Lipschitz是为了保证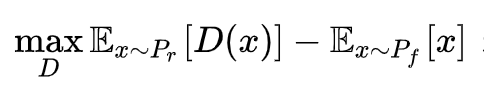
阅读完后续的笔记,我们将能找到答案~
参考论文:Wasserstein GANarxiv.org
参考链接:郑华滨:令人拍案叫绝的Wasserstein GAN
更多阅读
更多深度学习,GAN相关论文阅读笔记请关注深度学习论文阅读笔记专栏。
关于作者林小北:毕业于清华大学自动化系,京东算法工程师。
欢迎关注知乎专栏:https://zhuanlan.zhihu.com/c_1080771046889623552