导语
ICML (International Conference on Machine Learning) 是机器学习领域的顶级会议,由国际机器学习学会(ICML)举办,一般在每年的7-8月召开。在ICML 2020上,百度的收录论文中有三篇与梯度下降、反向传播相关,它们进一步阐释和改进了作为深度学习基础的梯度下降与反向传播技术,分别是:
1)RIFLE: Backpropagation in Depth for Deep Transfer Learning through Re-Initializing the Fully-connected LayEr
2)On the Noisy Gradient Descent that Generalizes as SGD
3)Scalable Differential Privacy with Certified Robustness in Adversarial Learning
随着深度学习在大数据时代的应用场景越来越广泛,研究者和使用者对于神经网络的准确率有越来越高的要求,这就离不开对训练神经网络中梯度下降算法(Gradient Descent, GD)与反向传播算法(Backpropagation)的理解与演进。在今年被收录的RIFLE: Backpropagation in Depth for Deep Transfer Learning through Re-Initializing the Fully-connected LayEr 一文中,百度基于传统的反向传播方法提出了可以应用于深度迁移学习的RIFLE(Re-Initializing the Fully-connected LayEr)算法,使得神经网络模型的训练更充分;在On the Noisy Gradient Descent that Generalizes as SGD一文中, 作者发现不同类别SGD梯度噪音在正则化模型训练的表现相当,并提出一种新颖的乘法噪音的理解,衍化成亦可适用于大批量SGD优化的算法;Scalable Differential Privacy with Certified Robustness in Adversarial Learning则应用梯度下降算法建立了差分隐私(Differential Privacy, DP)保护,对抗学习和认证稳健性之间的连结。
RIFLE算法:全连接层的再初始化,简洁有效提升准确度的新算法
传统的迁移学习中,使用预先训练的模型对深层卷积神经网络(CNN)进行微调有助于将从较大的数据集中学到的知识迁移到目标任务中。尽管目标训练数据集时常很小,迁移学习后模型的准确性也可以大大提高,但迁移学习后的模型权重通常和预训练模型权重接近,这个限制导致网络中部分参数在迭代中更新较少。为了解决这个问题,RIFLE算法应运而生。
RIFLE即Re-Initializing the Fully-connected LayEr,全连接层的再初始化。RIFLE为CNN的深层权重带来了有意义的更新,并改善了低层级的特征学习。实验表明,使用RIFLE可以显着提高深度迁移学习的准确性。在相同的场景下,RIFLE比其他已知的方法(dropout, dropconnect,stochastic depth, disturb label, cyclic learning rate等)的表现更好,测试精度可以提高0.5%–2%。经验案例和消融研究(ablation studies)进一步证实了RIFLE对于准确率的提升。

图1:使用SGD优化器的RIFLE算法
研究人员通过实验比较了RIFLE与已知方法的表现,以下是具体阐述。
1. 总体比较
研究人员用两种常见的精调算法,L^2和L^2-SP,测试了深度迁移学习算法。
1.1 与迁移学习的显式正则器的比较
实验发现,RIFLE稳定且显著地提升了L^2和L^2 -SP两种精调算法的表现。这证明了使用RIFLE在现有显式正则器上改善深度转移学习的可行性。
1.2 与算法+显式正则器的比较
在与dropout, dropconnect, cyclic learning rate和disturb label等方法的比较下,RIFLE的表现均更好。其中dropout和disturb label也表现较好,但在多数情况下不敌RIFLE。
2. 消融研究
为了研究哪部分对RIFLE最为关键,研究人员进行了消融研究。分析研究结果得知,算法的核心基础在于再初始化全连接层,而非周期学习率(cyclic learning rate)。
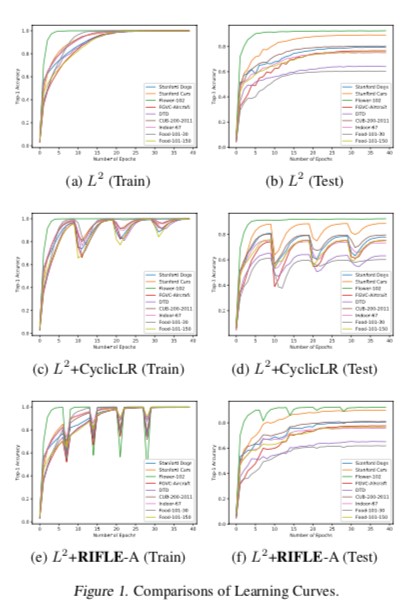
3. 学习曲线的比较
通过图2的学习曲线结果,可以看到,相比于周期学习率或传统训练程序,RIFLE导致模型的训练曲线震荡更大,表明训练过程中权重有较多调整。此外,通常通过模型测试曲线的趋势来评估它的泛化能力,观察图2中各个方法在测试集上的表现,研究人员发现RIFLE这种调整可以提升深度迁移学习的泛化能力。
图2:学习曲线的比较结果
总结来说,百度新提出的RIFLE算法通过在精调时随机训练的方式间歇性再初始化全连接层,使深度迁移学习的模型得到更充分的训练,从而提升准确率。
MSGD算法:建构对于梯度下降泛化性的行为的深层次理解
在反向传播中,梯度下降算法(Gradient Descent, GD)扮演了十分重要的角色。梯度下降(Gradient Descent, GD)是常常用于求解机器学习模型的参数的优化算法。使用梯度下降算法时,先定义损失函数,然后随机给定函数中参数的初始值,计算损失值,然后通过不断迭代的方式优化参数,在有限步数内,期望使损失函数取到最小值。对于一般的梯度下降来说,损失函数会涉及到模型中的每一个样本,导致计算量很大,于是产生了随机梯度下降(Stochastic Gradient Descent, SGD)和小批量梯度下降(Mini-batch Gradient Descent)、大批量梯度下降(Large-batch Gradient Descent)等方法。
随机梯度下降的损失函数每次只会随机选取到一个样本,这就大大简化了计算流程,同时加快了运算速度。但是每次随机选取一个样本可能会造成比较大的偏差,小批量梯度下降则是从全部样本中选取一定数量的样本计算损失值来减小偏差。严格意义上,随机梯度下降,即SGD每次迭代只选取一个样本,广义来说,小批量梯度下降也有时被当作SGD的一种。
近期研究发现,SGD事实上催生了一种正则化(regularization)效果。通过比较GD、SGD、小批量SGD、大批量SGD和GLD (Gradient Langevin Dynamic)之间的泛化能力,研究人员发现SGD的泛化能力强于GD,小批量SGD的泛化能力强于大批量SGD,GLD的泛化能力无法与SGD比较。为什么会产生这些现象呢?
第一,SGD每次选取的样本有一定的随机性,这个过程会造成噪音(noise),可以将SGD看作一种每次迭代有不偏(unbiased)噪音的确定算法[1],这种噪音可以称为梯度噪音(gradient noise);第二,小批量SGD的梯度噪声要比大批量SGD的梯度噪声振幅(magnitude)更广2;第三,即使调整到相同振幅,SGD噪音具有非平凡协方差结构,而不像GLD只是白噪声。
从以上讨论中可知,特定噪音可以有效对GD进行正则化。
因此可以说,SGD的梯度噪音对深度学习的泛化能力至关重要,过去的研究证实了振幅(magnitude)和协方差结构对梯度噪音的正则化有关键意义,但是对于噪音分布(distribution)的具体情况研究人员仍然没有一个清晰的了解。百度近期的研究提出一种新的结构:使用梯度矩阵与小批量抽样产生的抽样噪音相乘,来拟合梯度噪音。最新的研究成果主要有四大贡献:
- 提出了一种新颖的方式来模拟SGD噪音,即MSGD,使用梯度矩阵与小批量抽样产生的抽样噪音相乘。有噪音的梯度下降的类别则基于抽样噪音的类别。
- 探究了梯度噪音种类对正则化的影响:如果有合适的噪音振幅和协方差矩阵,研究人员通过理论和实验展示了噪音种类对正则化没有关键影响。
- 修正了两种基于高斯分布的梯度正则化噪音,一种使用了(缩放后)费希尔(Fisher)协方差,另一种使用了SGD的梯度协方差作为梯度噪音的协方差。通过分析其抽样噪音发现,两种情况等价。
- 由以上研究结果可知,噪音的类别对泛化能力的影响有限,研究人员提出了一种新的算法。这种算法针对不同类别的噪音都可以进行具有泛化能力的梯度下降。这种算法对大批量SGD的训练也同样适用,且不会对模型泛化能力造成负面影响。

图3:MSGD算法

图4:小批量MSGD算法

图5:MSGD的泛化能力
在图5中,横轴是迭代次数,纵轴是测试准确性。图5(a)中研究人员使用FashionMNIST作为训练集,随机抽去了1000个样本,随后训练了一个小型的卷积型网络;图5(b)中研究人员使用SVHN的25000个样本作为训练集,在没有批量标准化(batch normalization)的情况下训练了VGG-11;图5(c)中研究人员在没有应用数据增强(data augmentation)和权重衰减的情况下在CIFAR-10上面训练了ResNet-18。
为便于叙述,先介绍一些缩写:
- MSGD-Fisher:协方差是(缩放后)费希尔的高斯梯度噪音MSGD。
- MSGD-Cov:协方差是SGD协方差的高斯梯度噪音MSGD。
- MSGD-Bernoulli:伯努利(Bernoulli)抽样噪音的MSGD。
- MSGD-[Fisher-B]:使用费希尔估计的小批量样本数为B的MSGD-Fisher。
图4显示了MSGD-Cov在不同数据集和模型上的结果,这些结果表明即使分布类别不同,MSGD-Cov和传统SGD的泛化能力一样良好。更有趣的是,研究人员发现MSGD-Cov比vanilla SGD收敛得更快。
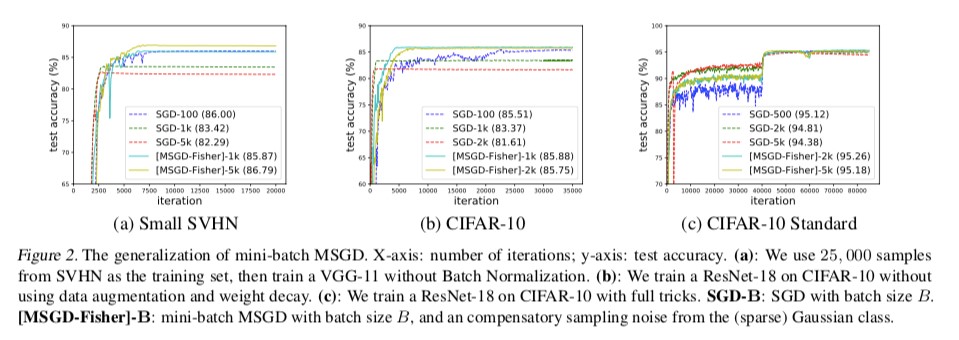
图6:小批量MSGD的泛化能力
在图6中,横轴是迭代次数,纵轴是测试准确性。图6(a)中研究人员使用SVHN的25000个样本作为训练集,在没有批量标准化的情况下训练了VGG-11;图6(b)中研究人员在没有应用数据增强(data augmentation)和权重衰减的情况下在CIFAR-10上面训练了ResNet-18;图6(c)中研究人员用全套方法在CIFAR-10上训练了ResNet-18。
从图6(a)(b)中看出,采取样本量为B的大批量数据集相比大批量样本有更好的泛化能力,且收敛速度更快。即使在CIFAR-10训练ResNet-18的实际过程中,大批量MSGD-Fisher有和小批量SGD一样的泛化能力,虽然大批量SGD的表现较差一些。由此,图6中的实证结果展现出小批量MSGD在实际应用中的广阔前景。
总结来看,在百度的最新研究成果改变了传统观念中认为SGD是GD增加特定类别噪音的想法,且提出MSGD的新算法,使得其泛化性和SGD同样良好,有助于更好地理解了梯度下降的泛化性及其行为。
此外,梯度下降法在保护数据安全的领域也有应用,在百度新的研究中使用梯度下降法建立了差分隐私(Differential Privacy, DP)保护,对抗学习和认证稳健性之间的连结。
参考文献
[1]Bottou, L. Stochastic gradient learning in neural networks. Proceedings of Neuro-Nımes, 91(8), 1991.
[2]Hochreiter, S. and Schmidhuber, J. Flat minima. Neural Computation, 9(1):1–42, 1997.
[3]Jastrze ̨bski, S., Kenton, Z., Arpit, D., Ballas, N., Fischer, A., Bengio, Y., and Storkey, A. Three factors influencing minima in sgd. arXiv preprint arXiv:1711.04623, 2017.
推荐阅读
欢迎转载,转载请说明作者及出处链接。更多AI相关技术欢迎关注嵌入式AI专栏。