【项目实践】从零开始学习Deep SORT+YOLO V3进行多目标跟踪（附注释项目代码）

转载自：AI人工智能初学者
作者：ChaucerG

1、跟踪基础知识简介

首先要说明一点，现在多目标跟踪算法的效果，与目标检测的结果息息相关，因为主流的多目标跟踪算法都是TBD（Tracking-by-Detecton）策略，SORT同样使用的是TBD，也就是说先检测，再跟踪。这也是跟踪领域的主流方法。所以，检测器的好坏将决定跟踪的效果。

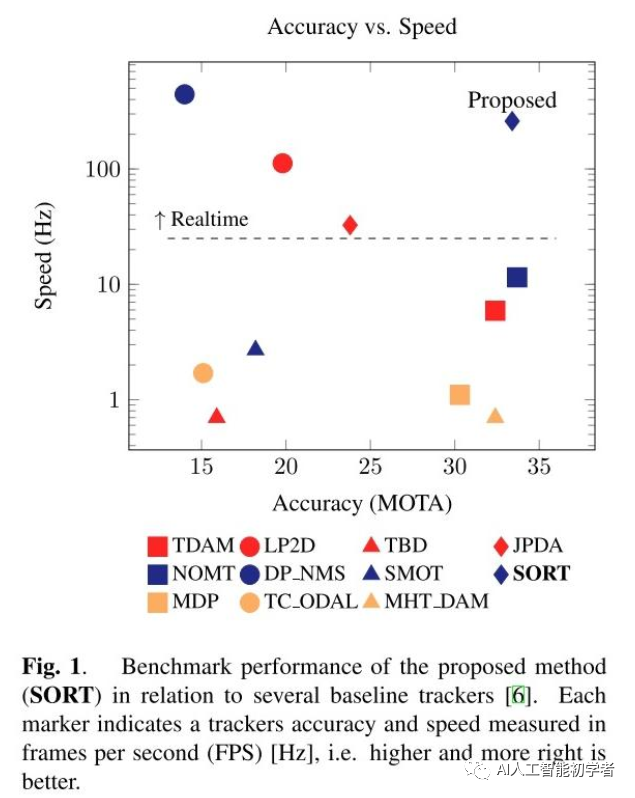
本文抛开目标检测（YOLO V3）不谈，主要看SORT的跟踪思路。SORT采用的是在线跟踪的方式，不使用未来帧的信息。在保持100fps以上的帧率的同时，也获得了较高的MOTA（在当时16年的结果中）。

1.1、SORT的3个主要贡献

利用强大的CNN检测器的检测结果来进行多目标跟踪；
使用基于卡尔曼滤波（Kalman filter）与匈牙利算法（Hungarian algorithm）的方法来进行跟踪；
开源了代码，为MOT领域提供一个新的baseline。

1.2、SORT算法的简单理解

跟踪之前，对所有目标已经完成检测；
第一帧进来时，以检测到的目标初始化并创建新的跟踪器，标注id；
后面帧进来时，先到卡尔曼滤波器（Kalman Filter）中得到由前面帧box产生的状态预测和协方差预测。求跟踪器所有目标状态与本帧检测的Box的IOU，通过匈牙利算法（Hungarian Algorithm），得到IOU最大的唯一匹配（数据关联部分），在去掉匹配值小于IOU\_threshold的匹配对；
用本帧中匹配到的目标检测Box去更新卡尔曼跟踪器，计算卡尔曼增益，状态更新和协方差更新。并将状态更新值输出，作为本帧的跟踪Box。对于本帧中没有匹配到的目标重新初始化跟踪器，卡尔曼跟踪器联合了历史跟踪记录，调节历史Box与本帧Box的残差，更好地匹配跟踪id。
其中卡尔曼滤波（Kalman filter）与匈牙利算法（Hungarian algorithm）对于大家来说可能是两个新名词。先简单解释一下，匈牙利算法是一种寻找二分图的最大匹配的算法，在多目标跟踪问题中可以简单理解为寻找前后两帧的若干目标的匹配最优解的一种算法。而卡尔曼滤波可以看作是一种运动模型，用来对目标的轨迹进行预测，并且使用确信度较高的跟踪结果进行预测结果的修正，是控制领域常用的一种算法。

1.3、卡尔曼滤波

1.3.1、卡尔曼滤波算法有两个基本假设

(1)、信息过程的足够精确的模型，是由白噪声所激发的线性(也可以是时变的) 动态系统;
(2)、每次的测量信号都包含着附加的白噪声分量。
当满足以上假设时，可以应用卡尔曼滤波算法。

1.3.2、问题描述与定义

定义一个随机离散时间过程的状态向量，该过程用一个离散随机差分方程描述：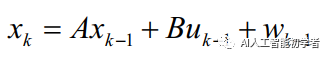
其中n维向量为k时刻的系统状态变量，n维向量是k-1时刻的系统状态变量。A是状态转移矩阵或者过程增益矩阵，是n×n阶方阵，它将k-1时刻状态和当前的k时刻状态联系起来。B是可选的控制输入 u∈Rl的增益，在大多数实际情况下并没有控制增益，所以这一项很愉快的变成零了。是n维向量，代表过程激励噪声，它对应了中每个分量的噪声，是期望为0，协方差为Q的高斯白噪声，。
再定义一个观测变量，得到观测方程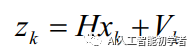：其中观测值是m阶向量，状态变量是n阶向量。H是m×n阶矩阵，代表状态变量对测量变量的增益。观测噪声是期望为0，协方差为R的高斯白噪声，~N(0,R)。

1.3.3、卡尔曼滤波算法步骤

卡尔曼滤波器可以分为时间更新方程和测量更新方程。时间更新方程（即预测阶段）根据前一时刻的状态估计值推算当前时刻的状态变量先验估计值和误差协方差先验估计值；测量更新方程（即更新阶段）负责将先验估计和新的测量变量结合起来构造改进的后验估计。时间更新方程和测量更新方程也被称为预测方程和校正方程。因此卡尔曼算法是一个递归的预测——校正方法。
(1)、预测(Prediction)：根据上一时刻(k-1时刻)的后验估计值来估计当前时刻(k时刻)的状态，得到k时刻的先验估计值，卡尔曼滤波器时间更新方程：

(2)、 更新(Update)：使用当前时刻的测量值来更正预测阶段估计值，得到当前时刻的后验估计值，卡尔曼滤波器状态更新方程：下面来一个个详细剖析每个参数：
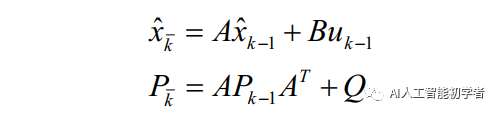
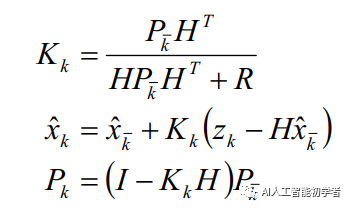
1、和 ：分别表示k-1时刻和k时刻的后验状态估计值，是滤波的结果之一，即更新后的结果，也叫最优估计(估计的状态，根据理论，我们不可能知道每时刻状态的确切结果所以叫估计)。
2、：k时刻的先验状态估计值，是滤波的中间计算结果，即根据上一时刻(k-1时刻)的最优估计预测的k时刻的结果，是预测方程的结果。
3、和：分别表示k-1时刻和k时刻的后验估计协方差(即和的协方差，表示状态的不确定度)，是滤波的结果之一。
4、:k时刻的先验估计协方差(的协方差)，是滤波的中间计算结果。
5、H：是状态变量到测量(观测)的转换矩阵，表示将状态和观测连接起来的关系，卡尔曼滤波里为线性关系，它负责将m维的测量值转换到n维，使之符合状态变量的数学形式，是滤波的前提条件之一。
6、：测量值(观测值)，是滤波的输入。
7、：滤波增益矩阵，是滤波的中间计算结果，卡尔曼增益，或卡尔曼系数。
8、A：状态转移矩阵，实际上是对目标状态转换的一种猜想模型。例如在机动目标跟踪中，状态转移矩阵常常用来对目标的运动建模，其模型可能为匀速直线运动或者匀加速运动。当状态转移矩阵不符合目标的状态转换模型时，滤波会很快发散。
9、Q：过程激励噪声协方差(系统过程的协方差)。该参数被用来表示状态转换矩阵与实际过程之间的误差。因为我们无法直接观测到过程信号，所以Q的取值是很难确定的。一般有两种思路：一是在某些稳定的过程可以假定它是固定的矩阵，通过寻找最优的Q值使滤波器获得更好的性能，这是调整滤波器参数的主要手段，Q一般是对角阵，且对角线上的值很小，便于快速收敛；二是在自适应卡尔曼滤波（AKF）中Q矩阵是随时间变化的。
10、R：表示测量噪声协方差，它是一个数值，这是和仪器相关的一个特性，作为已知条件输入滤波器。需要注意的是这个值过大过小都会使滤波效果变差，且R取值越小收敛越快，所以可以通过实验手段寻找合适的R值再利用它进行真实的滤波。
11、B：是将输入转换为状态的矩阵。
12、：实际观测和预测观测的残差，和卡尔曼增益一起修正先验(预测)，得到后验。

1.4、卡尔曼滤波的推导

更详细文末见文档，文档笔记中已经进行推导

1.5、卡尔曼滤波波代码注释

import numpy as np  
import scipy.linalg  
  
chi2inv95 = {  
            1: 3.8415,  
            2: 5.9915,  
            3: 7.8147,  
            4: 9.4877,  
            5: 11.070,  
            6: 12.592,  
            7: 14.067,  
            8: 15.507,  
            9: 16.919  
            }  
  
  
class KalmanFilter(object):  
    def __init__(self):  
        ndim, dt = 4, 1.  
  
        # 构建Kalman Filter的矩阵model,并初始化初始状态  
        self._motion_mat = np.eye(2 * ndim, 2 * ndim)  
        for i in range(ndim):  
            self._motion_mat[i, ndim + i] = dt  
              
        self._update_mat = np.eye(ndim, 2 * ndim)  
        self._std_weight_position = 1. / 20  
        self._std_weight_velocity = 1. / 160  
  
    def initiate(self, measurement):  
        mean_pos = measurement  
        mean_vel = np.zeros_like(mean_pos)  
        mean = np.r_[mean_pos, mean_vel]  
  
        std = [  
                2 * self._std_weight_position * measurement[3],  
                2 * self._std_weight_position * measurement[3],  
                1e-2,  
                2 * self._std_weight_position * measurement[3],  
                10 * self._std_weight_velocity * measurement[3],  
                10 * self._std_weight_velocity * measurement[3],  
                1e-5,  
                10 * self._std_weight_velocity * measurement[3]  
              ]  
  
        covariance = np.diag(np.square(std))  
        return mean, covariance  
  
    def predict(self, mean, covariance):  
        # 相当于得到t时刻估计值  
        # Q 预测过程中噪声协方差  
        std_pos = [  
                    self._std_weight_position * mean[3],  
                    self._std_weight_position * mean[3],  
                    1e-2,  
                    self._std_weight_position * mean[3]  
                  ]  
        std_vel = [  
                    self._std_weight_velocity * mean[3],  
                    self._std_weight_velocity * mean[3],  
                    1e-5,  
                    self._std_weight_velocity * mean[3]  
                  ]  
        # np.r_ 按列连接两个矩阵  
        # 初始化噪声矩阵Q  
        motion_cov = np.diag(np.square(np.r_[std_pos, std_vel]))  
        # x' = Fx  
        mean = np.dot(self._motion_mat, mean)  
        # P' = FPF^T+Q  
        covariance = np.linalg.multi_dot((self._motion_mat, covariance, self._motion_mat.T)) + motion_cov  
  
        return mean, covariance  
  
    def project(self, mean, covariance):  
        # 将状态分布投影到测量空间  
        std = [  
            self._std_weight_position * mean[3],  
            self._std_weight_position * mean[3],  
            1e-1,  
            self._std_weight_position * mean[3]  
             ]  
        # 初始化噪声矩阵R  
        innovation_cov = np.diag(np.square(std))  
        # 将均值向量映射到检测空间，即Hx'  
        mean = np.dot(self._update_mat, mean)  
        # 将协方差矩阵映射到检测空间，即HP'H^T  
        covariance = np.linalg.multi_dot((self._update_mat, covariance, self._update_mat.T))  
        return mean, covariance + innovation_cov  
  
    def update(self, mean, covariance, measurement):  
        # 计算 Kalman Filter的Correction Step==>Update Step  
        # 将mean和covariance映射到检测空间，得到Hx'和S  
        projected_mean, projected_cov = self.project(mean, covariance)  
        # 矩阵分解  
        chol_factor, lower = scipy.linalg.cho_factor(projected_cov, lower=True, check_finite=False)  
        # 计算卡尔曼增益K  
        kalman_gain = scipy.linalg.cho_solve((chol_factor, lower), np.dot(covariance, self._update_mat.T).T, check_finite=False).T  
        # z - Hx'  
        innovation = measurement - projected_mean  
        # x = x' + Ky  
        new_mean = mean + np.dot(innovation, kalman_gain.T)  
        # P = (I - KH)P'  
        new_covariance = covariance - np.linalg.multi_dot((kalman_gain, projected_cov, kalman_gain.T))  
        return new_mean, new_covariance  
  
    def gating_distance(self, mean, covariance, measurements, only_position=False):  
        # 计算系统的预测优化值  
        mean, covariance = self.project(mean, covariance)  
        if only_position:  
            mean, covariance = mean[:2], covariance[:2, :2]  
            measurements = measurements[:, :2]  
  
        cholesky_factor = np.linalg.cholesky(covariance)  
        d = measurements - mean  
        z = scipy.linalg.solve_triangular(cholesky_factor, d.T, lower=True, check_finite=False, overwrite_b=True)  
        squared_maha = np.sum(z * z, axis=0)  
        return squared_maha

1.6、匈牙利算法

匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法，并推动了后来的原始对偶方法。美国数学家哈罗德·库恩于 1955 年提出该算法。此算法之所以被称作匈牙利算法，是因为算法很大一部分是基于以前匈牙利数学家 Dénes Kőnig 和 Jenő Egerváry 的工作之上创建起来的。
说明一下匈牙利算法的流程：

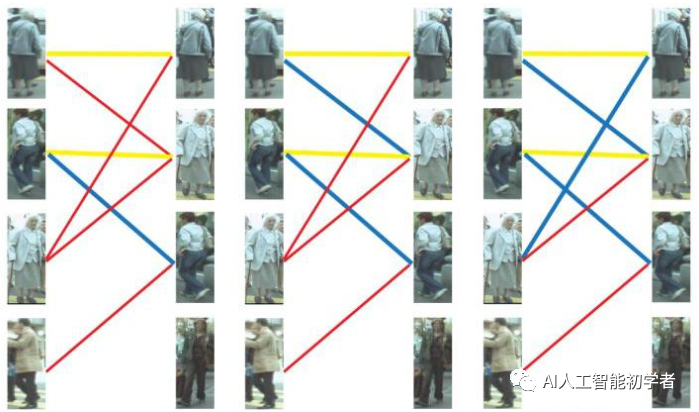
以上图为例，假设左边的四张图是我们在第N帧检测到的目标(U)，右边四张图是我们在第N+1帧检测到的目标(V)。红线连起来的图，是我们的算法认为是同一行人可能性较大的目标。由于算法并不是绝对理想的，因此并不一定会保证每张图都有一对一的匹配，一对二甚至一对多，再甚至多对多的情况都时有发生。这时我们怎么获得最终的一对一跟踪结果呢？我们来看匈牙利算法是怎么做的。
第一步：
首先给左1进行匹配，发现第一个与其相连的右1还未匹配，将其配对，连上一条蓝线。

第二步：
接着匹配左2，发现与其相连的第一个目标右2还未匹配，将其配对。

第三步：
接下来是左3，发现最优先的目标右1已经匹配完成了，怎么办呢？我们给之前右1的匹配对象左1分配另一个对象(黄色表示这条边被临时拆掉)

可以与左1匹配的第二个目标是右2，但右2也已经有了匹配对象，怎么办呢？我们再给之前右2的匹配对象左2分配另一个对象（注意这个步骤和上面是一样的，这是一个递归的过程）。

此时发现左2还能匹配右3，那么之前的问题迎刃而解了，回溯回去。左2对右3，左1对右2，左3对右1。

所以第三步最后的结果就是：

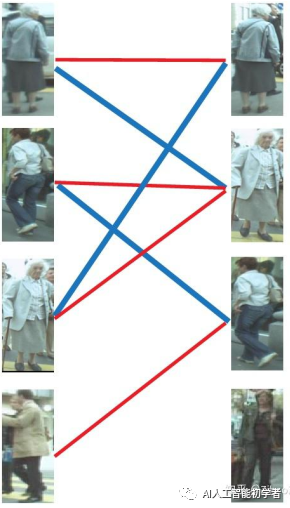
第四步：最后是左4，很遗憾，按照第三步的节奏我们没法给左4腾出来一个匹配对象，只能放弃对左4的匹配，匈牙利算法流程至此结束。蓝线就是我们最后的匹配结果。至此我们找到了这个二分图的一个最大匹配。
最终的结果是我们匹配出了三对目标，由于候选的匹配目标中包含了许多错误的匹配红线（边），所以匹配准确率并不高。可见匈牙利算法对红线连接的准确率要求很高，也就是要求我们运动模型、外观模型等部件必须进行较为精准的预测，或者预设较高的阈值，只将置信度较高的边才送入匈牙利算法进行匹配，这样才能得到较好的结果。
匈牙利算法的流程大家看到了，有一个很明显的问题相信大家也发现了，按这个思路找到的最大匹配往往不是我们心中的最优。匈牙利算法将每个匹配对象的地位视为相同，在这个前提下求解最大匹配。这个和我们研究的多目标跟踪问题有些不合，因为每个匹配对象不可能是同等地位的，总有一个真实目标是我们要找的最佳匹配，而这个真实目标应该拥有更高的权重，在此基础上匹配的结果才能更贴近真实情况。

2、Deep SORT 目标跟踪算法

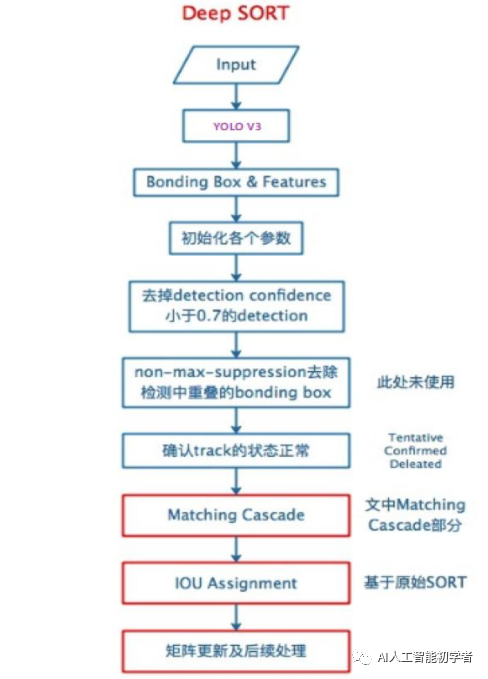
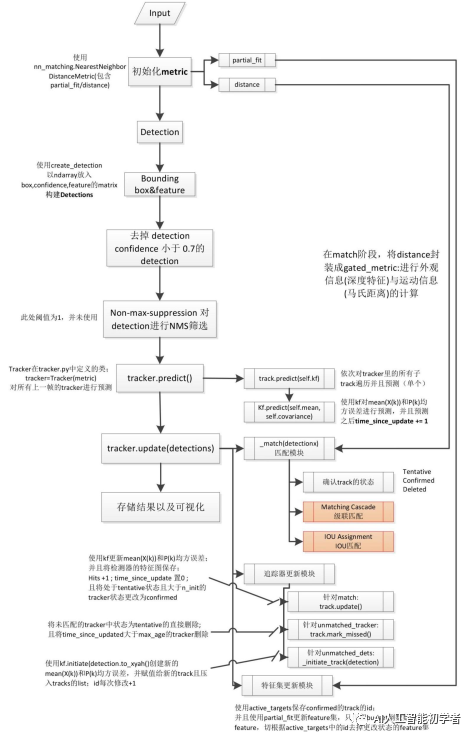
DeepSort中最大的特点是加入外观信息，借用了ReID领域模型来提取特征，减少了ID switch的次数。整体流程图如下：

可以看出，Deep SORT算法在SORT算法的基础上增加了级联匹配(Matching Cascade)+新轨迹的确认(confirmed)。总体流程就是：

卡尔曼滤波器预测轨迹 Tracks；
使用匈牙利算法将预测得到的轨迹 Tracks 和当前帧中的 detections 进行匹配(级联匹配和 IOU 匹配)；
卡尔曼滤波更新。

2.1、Deep SORT相对于SORT的改进

整体框架没有大改，还是延续了卡尔曼滤波加匈牙利算法的思路，在这个基础上增加了Deep Association Metric。Deep Association Metric其实就是在大型行人重识别网络上学习的一个行人鉴别网络。目的是区分出不同的行人。个人感觉很类似于典型的行人重识别网络。输出行人图片，输出一组向量，通过比对两个向量之间的距离，来判断两副输入图片是否是同一个行人。

2.2、级联匹配

级联匹配的目的：当一个目标长时间被遮挡之后，kalman滤波预测的不确定性就会大大增加，状态空间内的可观察性就会大大降低。假如此时两个追踪器竞争同一个检测结果的匹配权，往往遮挡时间较长的那条轨迹的马氏距离更小，使得检测结果更可能和遮挡时间较长的那条轨迹相关联，这种不理想的效果往往会破坏追踪的持续性。这么理解吧，假设本来协方差矩阵是一个正态分布，那么连续的预测不更新就会导致这个正态分布的方差越来越大，那么离均值欧氏距离远的点可能和之前分布中离得较近的点获得同样的马氏距离值。所以，作者使用了级联匹配来对更加频繁出现的目标赋予优先权。当然同样也有弊端：可能导致一些新产生的轨迹被连接到了一些旧的轨迹上。但这种情况较少。

上图非常清晰地解释了如何进行级联匹配，首先使用外观模型(ReID)和运动模型(马氏距离)来计算相似度矩阵，得到cost矩阵以及门控矩阵，用于限制代价矩阵中过大的值。然后则是级联匹配的数据关联步骤，匹配过程是一个循环(max age个迭代，默认为70)，也就是从missing age=0到missing age=70的轨迹和Detections进行匹配，没有丢失过的轨迹优先匹配，丢失较为久远的就靠后匹配。通过这部分处理，可以重新将被遮挡目标找回，降低被遮挡然后再出现的目标发生的ID Switch 次数。
将Detection和Track进行匹配，所以出现几种情况：

Detection和Track匹配，也就是 Matched Tracks。普通连续跟踪的目标都属于这种情况，前后两帧都有目标，能够匹配上。
Detection 没有找到匹配的Track，也就是Unmatched Detections。图像中突然出现新的目标的时候，Detection无法在之前的Track找到匹配的目标。
Track 没有找到匹配的Detection，也就是Unmatched Tracks。连续追踪的目标超出图像区域，Track无法与当前任意一个 Detection 匹配。
以上没有涉及一种特殊的情况，就是两个目标遮挡的情况。刚刚被遮挡的目标的Track也无法匹配Detection，目标暂时从图像中消失。之后被遮挡目标再次出现的时候，应该尽量让被遮挡目标分配的ID不发生变动，减少IDSwitch 出现的次数，这就需要用到级联匹配了。

2.3、IOU Assignment

这个方法是在SORT中被提出的。又是比较陌生的名词。实际上匈牙利算法可以理解成“尽量多”的一种思路，比如说A检测器可以和a，c跟踪器完成匹配（与a匹配置信度更高），但是B检测器只能和a跟踪器完成匹配。那在算法中，就会让A与c完成匹配，B 与a完成匹配，而降低对于置信度的考虑。所以算法的根本目的并不是在于匹配的准不准，而是在于尽量多的匹配上，这也就是在deepsort中作者添加级联匹配与马氏距离与余弦距离的根本目的，因为仅仅使用匈牙利算法进行匹配特别容易造成 ID switch，就是一个检测框id不停地进行更换，缺乏准确性与鲁棒性。那什么是匹配的置信度高呢，其实在这里，作者使用的是 IOU 进行衡量，计算检测器与跟踪器的IOU，将这个作为置信度的高低（比较粗糙）。

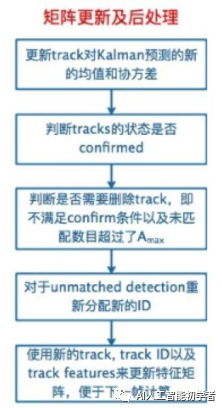
2.4、矩阵更新后续处理

2.5、代码流程图

3、 Deep SORT代码解析

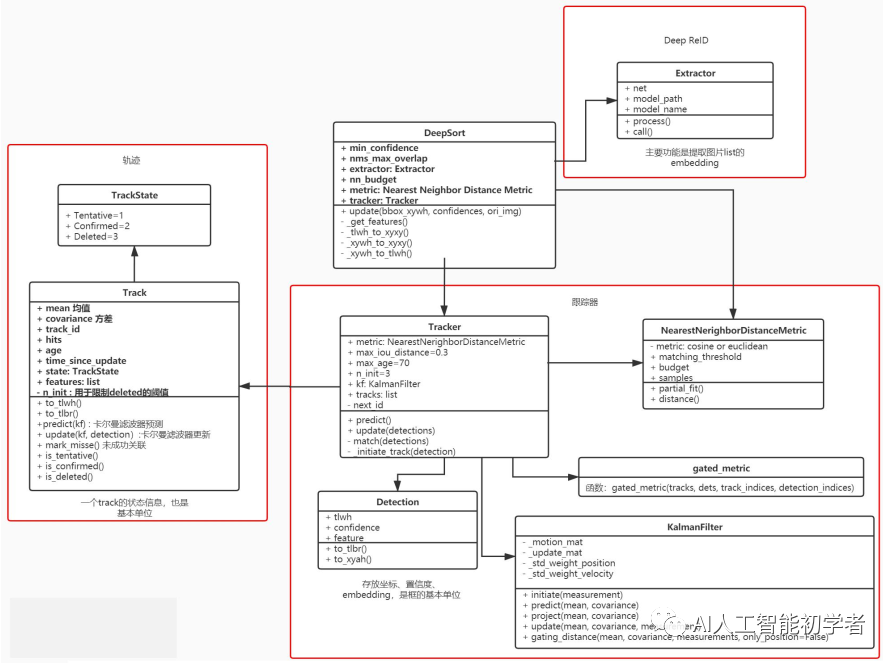
DeepSort 是核心类，调用其他模块，大体上可以分为三个模块：

ReID 模块，用于提取表观特征，原论文中是生成了128维的embedding。
Track 模块，轨迹类，用于保存一个Track的状态信息，是一个基本单位。
Tracker 模块，Tracker模块掌握最核心的算法，卡尔曼滤波和匈牙利算法都是通过调用这个模块来完成的。

3.1、核心模块

3.1.1、Detection类

import numpy as np  
  
class Detection(object):  
    #This class represents a bounding box detection in a single image.  
    def __init__(self, tlwh, confidence, feature):  
        self.tlwh = np.asarray(tlwh, dtype=np.float)  
        self.confidence = float(confidence)  
        self.feature = np.asarray(feature, dtype=np.float32)  
  
    def to_tlbr(self):  
        ret = self.tlwh.copy()  
        ret[2:] += ret[:2]  
        return ret  
  
    def to_xyah(self):  
        ret = self.tlwh.copy()  
        ret[:2] += ret[2:] / 2  
        ret[2] /= ret[3]  
        return ret

Detection 类用于保存通过目标检测器得到的一个检测框，包含 top left 坐标+框的宽和高，以及该 bbox 的置信度还有通过 reid 获取得到的对应的 embedding。除此以外提供了不同 bbox 位置格式的转换方法：

tlwh: 代表左上角坐标+宽高
tlbr: 代表左上角坐标+右下角坐标
xyah: 代表中心坐标+宽高比+高

3.1.2、Track类

class Track:  
    # 一个轨迹的信息，包含(x,y,a,h) & v  
    """  
    A single target track with state space `(x, y, a, h)` and associated  
    velocities, where `(x, y)` is the center of the bounding box, `a` is the  
    aspect ratio and `h` is the height.  
    """  
  
    def __init__(self, mean, covariance, track_id, n_init, max_age,  
                 feature=None):  
        # max age是一个存活期限，默认为70帧,在  
        self.mean = mean  
        self.covariance = covariance  
        self.track_id = track_id  
        self.hits = 1   
        # hits和n_init进行比较  
        # hits每次update的时候进行一次更新（只有match的时候才进行update）  
        # hits代表匹配上了多少次，匹配次数超过n_init就会设置为confirmed状态  
        self.age = 1 # 没有用到，和time_since_update功能重复  
        self.time_since_update = 0  
        # 每次调用predict函数的时候就会+1  
        # 每次调用update函数的时候就会设置为0  
  
        self.state = TrackState.Tentative  
        self.features = []  
        # 每个track对应多个features, 每次更新都将最新的feature添加到列表中  
        if feature is not None:  
            self.features.append(feature)  
  
        self._n_init = n_init  # 如果连续n_init帧都没有出现失配，设置为deleted状态  
        self._max_age = max_age  # 上限

Track类主要存储的是轨迹信息，mean和covariance是保存的框的位置和速度信息，track\_id代表分配给这个轨迹的ID。state代表框的状态，有三种：

Tentative：不确定态，这种状态会在初始化一个Track的时候分配，并且只有在连续匹配上n\_init帧才会转变为确定态。如果在处于不确定态的情况下没有匹配上任何detection，那将转变为删除态；
Confirmed：确定态，代表该Track确实处于匹配状态。如果当前Track属于确定态，但是失配连续达到max age次数的时候，就会被转变为删除态；
Deleted：删除态，说明该Track已经失效。
max\_age：代表一个Track存活期限，他需要和time\_since\_update变量进行比对。time\_since\_update是每次轨迹调用predict函数的时候就会+1，每次调用predict的时候就会重置为0，也就是说如果一个轨迹长时间没有update(没有匹配上)的时候，就会不断增加，直到time\_since\_update超过max age(默认70)，将这个Track从Tracker中的列表删除。
Hits：代表连续确认多少次，用在从不确定态转为确定态的时候。每次Track进行update的时候，hits就会+1, 如果hits>n\_init(默认为3)，也就是连续三帧的该轨迹都得到了匹配，这时候才将不确定态转为确定态。

3.1.3、ReID特征提取部分

ReID网络是独立于目标检测和跟踪器的模块，功能是提取对应bounding box中的feature,得到一个固定维度的embedding作为该bbox的代表，供计算相似度时使用。

class Extractor(object):  
    def __init__(self, model_name, model_path, use_cuda=True):  
        self.net = build_model(name=model_name,  
                               num_classes=96)  
        self.device = "cuda" if torch.cuda.is_available(  
        ) and use_cuda else "cpu"  
        state_dict = torch.load(model_path)['net_dict']  
        self.net.load_state_dict(state_dict)  
        print("Loading weights from {}... Done!".format(model_path))  
        self.net.to(self.device)  
        self.size = (128,128)  
        self.norm = transforms.Compose([  
            transforms.ToTensor(),  
            transforms.Normalize([0.3568, 0.3141, 0.2781],  
                                 [0.1752, 0.1857, 0.1879])  
        ])  
  
    def _preprocess(self, im_crops):  
  
        def _resize(im, size):  
            return cv2.resize(im.astype(np.float32) / 255., size)  
  
        im_batch = torch.cat([  
            self.norm(_resize(im, self.size)).unsqueeze(0) for im in im_crops  
        ],dim=0).float()  
        return im_batch  
  
    def __call__(self, im_crops):  
        im_batch = self._preprocess(im_crops)  
        with torch.no_grad():  
            im_batch = im_batch.to(self.device)  
            features = self.net(im_batch)  
        return features.cpu().numpy()

3.1.4、NearestNeighborDistanceMetric类

计算欧氏距离

def _pdist(a, b):  
    # 用于计算成对的平方距离  
    # a NxM 代表N个对象，每个对象有M个数值作为embedding进行比较  
    # b LxM 代表L个对象，每个对象有M个数值作为embedding进行比较  
    # 返回的是NxL的矩阵，比如dist[i][j]代表a[i]和b[j]之间的平方和距离  
    # 实现见：https://blog.csdn.net/frankzd/article/details/80251042  
    a, b = np.asarray(a), np.asarray(b)  # 拷贝一份数据  
    if len(a) == 0 or len(b) == 0:  
        return np.zeros((len(a), len(b)))  
    a2, b2 = np.square(a).sum(axis=1), np.square(  
        b).sum(axis=1)  # 求每个embedding的平方和  
    # sum(N) + sum(L) -2 x [NxM]x[MxL] = [NxL]  
    r2 = -2. * np.dot(a, b.T) + a2[:, None] + b2[None, :]  
    r2 = np.clip(r2, 0., float(np.inf))  
    return r2

计算余弦距离

def _cosine_distance(a, b, data_is_normalized=False):  
    # a和b之间的余弦距离  
    # a : [NxM] b : [LxM]  
    # 余弦距离 = 1 - 余弦相似度  
    # https://blog.csdn.net/u013749540/article/details/51813922  
    if not data_is_normalized:  
        # 需要将余弦相似度转化成类似欧氏距离的余弦距离。  
        a = np.asarray(a) / np.linalg.norm(a, axis=1, keepdims=True)  
        #  np.linalg.norm 操作是求向量的范式，默认是L2范式，等同于求向量的欧式距离。  
        b = np.asarray(b) / np.linalg.norm(b, axis=1, keepdims=True)  
    return 1. - np.dot(a, b.T)

3.1.6、Tracker类

Tracker类是最核心的类，Tracker中保存了所有的轨迹信息，负责初始化第一帧的轨迹、卡尔曼滤波的预测和更新、负责级联匹配、IOU匹配等等核心工作。

class Tracker:  
    def __init__(self, metric, max_iou_distance=0.7, max_age=30, n_init=3):  
        self.metric = metric  
        self.max_iou_distance = max_iou_distance  
        self.max_age = max_age  
        self.n_init = n_init  
  
        self.kf = kalman_filter.KalmanFilter()  
        self.tracks = []  
        self._next_id = 1  
  
    def predict(self):  
        for track in self.tracks:  
            track.predict(self.kf)  
  
    def update(self, detections):  
        # Run matching cascade.  
        matches, unmatched_tracks, unmatched_detections = \  
            self._match(detections)  
  
        # Update track set.  
        for track_idx, detection_idx in matches:  
            self.tracks[track_idx].update(  
                self.kf, detections[detection_idx])  
        for track_idx in unmatched_tracks:  
            self.tracks[track_idx].mark_missed()  
        for detection_idx in unmatched_detections:  
            self._initiate_track(detections[detection_idx])  
        self.tracks = [t for t in self.tracks if not t.is_deleted()]  
  
        # Update distance metric.  
        active_targets = [t.track_id for t in self.tracks if t.is_confirmed()]  
        features, targets = [], []  
        for track in self.tracks:  
            if not track.is_confirmed():  
                continue  
            features += track.features  
            targets += [track.track_id for _ in track.features]  
            track.features = []  
        self.metric.partial_fit(  
            np.asarray(features), np.asarray(targets), active_targets)  
  
    def _match(self, detections):  
        # 主要功能是进行匹配，找到匹配的，未匹配的部分  
        def gated_metric(tracks, dets, track_indices, detection_indices):  
            # 功能： 用于计算track和detection之间的距离，代价函数，需要使用在KM算法之前  
            features = np.array([dets[i].feature for i in detection_indices])  
            targets = np.array([tracks[i].track_id for i in track_indices])  
            # 1. 通过最近邻计算出代价矩阵 cosine distance  
            cost_matrix = self.metric.distance(features, targets)  
            # 2. 计算马氏距离,得到新的状态矩阵  
            cost_matrix = linear_assignment.gate_cost_matrix(self.kf, cost_matrix, tracks, dets, track_indices, detection_indices)  
  
            return cost_matrix  
  
        # 划分不同轨迹的状态  
        confirmed_tracks = [i for i, t in enumerate(self.tracks) if t.is_confirmed()]  
        unconfirmed_tracks = [i for i, t in enumerate(self.tracks) if not t.is_confirmed()]  
  
        # 进行级联匹配，得到匹配的track、不匹配的track、不匹配的detection  
        '''  
        !!!!!!!!!!!  
        级联匹配  
        !!!!!!!!!!!  
        '''  
        # gated_metric->cosine distance  
        # 仅仅对确定态的轨迹进行级联匹配  
        matches_a, unmatched_tracks_a, unmatched_detections = \  
            linear_assignment.matching_cascade(  
                gated_metric, self.metric.matching_threshold, self.max_age,  
                self.tracks, detections, confirmed_tracks)  
  
        # 将所有状态为未确定态的轨迹和刚刚没有匹配上的轨迹组合为iou_track_candidates，  
        # 进行IoU的匹配  
        iou_track_candidates = unconfirmed_tracks + [  
            k for k in unmatched_tracks_a if  
            self.tracks[k].time_since_update == 1]  
        # 未匹配  
        unmatched_tracks_a = [  
            k for k in unmatched_tracks_a if  
            self.tracks[k].time_since_update != 1]  
        '''  
        !!!!!!!!!!!  
        IOU 匹配  
        对级联匹配中还没有匹配成功的目标再进行IoU匹配  
        !!!!!!!!!!!  
        '''  
        # 虽然和级联匹配中使用的都是min_cost_matching作为核心，  
        # 这里使用的metric是iou cost和以上不同  
        matches_b, unmatched_tracks_b, unmatched_detections = \  
            linear_assignment.min_cost_matching(  
                iou_matching.iou_cost, self.max_iou_distance, self.tracks,  
                detections, iou_track_candidates, unmatched_detections)  
  
        matches = matches_a + matches_b  
        unmatched_tracks = list(set(unmatched_tracks_a + unmatched_tracks_b))  
        return matches, unmatched_tracks, unmatched_detections  
  
    def _initiate_track(self, detection):  
        mean, covariance = self.kf.initiate(detection.to_xyah())  
        self.tracks.append(Track(  
            mean, covariance, self._next_id, self.n_init, self.max_age,  
            detection.feature))  
        self._next_id += 1

4、项目结果展示

视频可见：【项目实践】从零开始学习Deep SORT+YOLO V3进行多目标跟踪（附注释项目代码）

当前的目标检车算法是yolo v3，后期会更新yolo v4、yolo v5以及Center Net的方法；这里的测试视频是小编在马路边用手机录制的，有点抖动，真么辛苦看完给个转发呗！！！！

参考：

https://blog.csdn.net/wccsu1994/article/details/84643221
https://blog.csdn.net/u013453604/article/details/50301477
https://zhuanlan.zhihu.com/p/62981901
https://blog.csdn.net/yiran103/article/details/89421140
https://zhuanlan.zhihu.com/p/133678626
https://blog.csdn.net/weixin\_40802676/article/details/97240063
https://zhuanlan.zhihu.com/p/62858357
SORT官方代码：https://github.com/abewley/sort
DeepSORT官方代码：https://github.com/nwojke/deep\_sort
奇点大佬keras实现DeepSORT: https://github.com/Qidian213/deep\_sort\_yolov3
CenterNet作检测器的DeepSORT: https://github.com/xingyizhou/CenterTrack
JDE Github地址: https://github.com/Zhongdao/Towards-Realtime-MOT
https://github.com/pprp/deep\_sort\_yolov3\_pytorch
https://github.com/kimyoonyoung/centerNet-deep-sort
https://arxiv.org/abs/1703.07402
https://github.com/pprp/SimpleCVReproduction/tree/master/deep\_sort-master
GiantPandaCV公众号：多目标跟踪快速入门教程

声明：转载请说明出处

推荐专栏文章

更多嵌入式AI算法部署等请关注极术嵌入式AI专栏。