HDLBits：在线学习 Verilog （二十四 · Problem 115-119） - 极术社区

转载自：知乎
作者：ljgibbs

Problem 115 Rule90

牛刀小试

Rule90 是一道根据一些有趣的规则来生成一维序列的题目。
规则很简单。一维序列中元素有 1,0 两种状态，分别对应开，关状态。
在每个时钟边沿到来时刻，元素的下一个状态为元素相邻两个元素的异或。
下表更详细地给出了跳变的规则，（可以视为状态转移表），元素下一个状态可以视作输出，输入为元素本身的状态与相应两个相邻元素的当前状态。

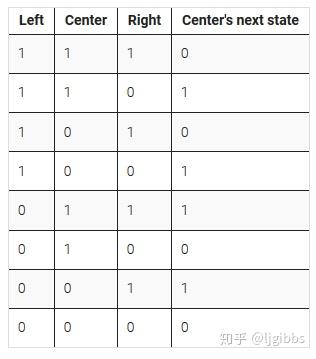
by the way,本题题目中的 Rule90 来自于上表中的 next state 这一列: 01011010 = 8'd90。
对于需要实现的电路，创建一个拥有 512 个元素的序列 (q[511:0])，每个时钟周期按照上述规则变换。load 信号有效时，序列更新 data 信号值为初始值。另外假设所有边界的值为 0 (q[-1] 以及 q[512])

解答与分析

module top_module(
    input clk,
    input load,
    input [511:0] data,
    output reg[511:0] q ); 
    
    int i;
    always @(posedge clk ) begin
        if(load)
            q <= data;
        else begin
            q[0]        <=  q[1] ^ 0;
            q[511]      <=  0 ^ q[510];
            for(i = 1; i<511;i=i+1)
                q[i] <= q[i - 1] ^ q[i + 1]; 
        end
    end
endmodule

解答中单列了两种特殊情况，q[0] 以及 q[511] ,因为他们的左侧或者右侧元素并不存在，题目中将其设定为 0.
除此之外的情况，使用 for 循环，状态转移当前状态左右邻居值的异或结果，其中左邻居指的是高位，右邻居指的是低位，是一种大端格式。
其实也可以不单列出特殊情况，比如本题的参考解答（原作者实在厉害，在下佩服）

module top_module(
    input clk,
    input load,
    input [511:0] data,
    output reg [511:0] q);
    
    always @(posedge clk) begin
        if (load)
            q <= data;    // Load the DFFs with a value.
        else begin
            // At each clock, the DFF storing each bit position becomes the XOR of its left neighbour
            // and its right neighbour. Since the operation is the same for every
            // bit position, it can be written as a single operation on vectors.
            // The shifts are accomplished using part select and concatenation operators.
            
            //     left           right
            //  neighbour       neighbour
            q <= q[511:1] ^ {q[510:0], 1'b0} ;
        end
    end
endmodule

异或左右邻居矩阵，左右邻居矩阵分别是原矩阵右移或者左移并补零得到，十分简练。

Problem 116 Rule110

牛刀小试

Rule110 还是一道根据有趣的规则来生成一维序列的题目，比如用于：

https://en.wikipedia.org/wiki/Turing\_completenessen.wikipedia.org

规则：一维序列中元素有 1,0 两种状态，分别对应开，关状态。

在每个时钟边沿到来时刻，元素的下一个状态取决于元素本身的状态与前后两个相邻元素的当前状态。下表详细地给出了跳变的规则。

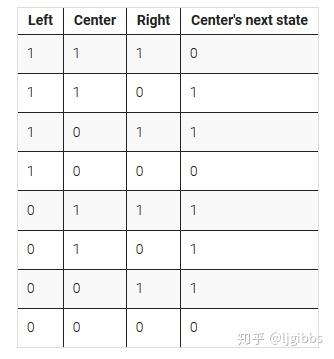
题目中的 Rule110 来自于上表中的 next state 这一列: 01101110= 8'd110。

对于需要实现的电路，创建一个拥有 512 个元素的序列 (q[511:0])，每个时钟周期按照上述规则变换。load 信号有效时，序列更新 data 信号值为初始值。另外假设所有边界的值为 0 (q[-1] q[512])

解答与分析

本题与上一题的区别在于没有给出具体的此态生成关系，比如上一题中的异或。所以我们首先需要找出状态转移规则。我们把上述的状态转移表转换为一个真值表来寻找转换规则，真值表对应的是三个输入信号：left，center，right，一个输出信号：next\_state。

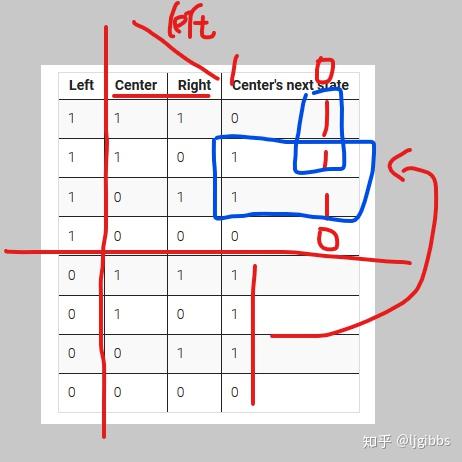
根据卡诺图可以得到:OUT = Center ^ Right + (Center · ~Left )
找到转移关系后，后续的解答就和上一题相同。

module top_module(
    input clk,
    input load,
    input [511:0] data,
    output reg[511:0] q
); 
    int i;
    always @(posedge clk ) begin
        if(load)
            q <= data;
        else begin
            q[0]        <=  q[0];
            q[511]      <=  (q[511] ^ q[510] )|| ( q[510] );
            for(i = 1; i<511;i=i+1)
                q[i] <= (q[i] ^ q[i - 1] )|| (!q[i+1] & q[i-1]); 
        end
    end
endmodule

Problem 117 Conwaylift/conway's game of life 16x16

牛刀小试

作为前两题的升级版，本题的变换工作在一个二维矩阵上，是一个二维序列生成器。
游戏规则如下：元素的下一个状态取决于当前状态九宫格中的 8 个邻居元素中 1 的个数，当邻居有 n 个 1 时：

0-1 ，元素变为 0
2 ，元素保持不变
3 ，元素变为 1
4+ ，元素变为 0

方便做题起见，本题中的这个二维矩阵设定为 16x16，广义上可以是无限的。
为了让事情变得更加有趣，这个16x16 矩阵的边界进行循环处理，回卷到对边，打个比方，上边界的上一行为下边界，左边界的左一列为右边界。

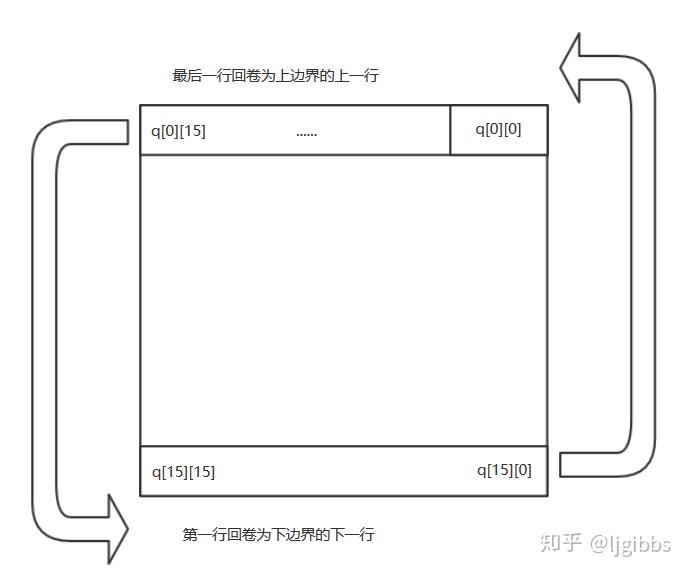
上下边界回卷示意，左右边界同理
所以对元素 (0,0) 来说，共有 8 个邻居 : (15,1), (15,0), (15,15), (0,1), (0,15), (1,1), (1,0) 以及 (1,15)。
这个 16x16 矩阵表示为 256bit 长度的向量 q，其中 q[15:0] 代表第一行，q[31:16] 代表第二行，以此类推。
HDLBit 支持使用 SystemVerilog，所以你也可以使用二维向量表示这个矩阵。load 信号有效时，更新 q 信号值为初始值 data, q 每个周期变换一次。

解答与分析

module top_module(
    input clk,
    input load,
    input [255:0] data,
    output [255:0] q ); 

    reg [15:0] q_2d [15:0]; //2-d q
    wire [2:0] nghbr_num [255:0];
    int idx_i_d,idx_i_u,idx_j_r,idx_j_l,i,j;

    //count num of neighbours
    always@(*) begin
        for(i = 0 ; i < 16 ; i = i + 1) begin
            for(j = 0 ; j < 16 ; j = j + 1) begin
                idx_i_u = (i == 0) ? i-1+16 :i-1; //up idx
                idx_i_d = (i == 15)? i+1-16 :i+1; //down idx
                idx_j_l = (j == 0) ? j-1+16 :j-1; //left idx
                idx_j_r = (j == 15)? j+1-16 :j+1; //right idx
                nghbr_num[i*16+j] = q_2d[idx_i_u][idx_j_l] + q_2d[idx_i_u][j  ] + q_2d[idx_i_u][idx_j_r]
                                +   q_2d[i      ][idx_j_l]                      + q_2d[i      ][idx_j_r]
                                +   q_2d[idx_i_d][idx_j_l] + q_2d[idx_i_d][j  ] + q_2d[idx_i_d][idx_j_r];
            end
        end
    end

    //next state transform base on num of neighbours
    always @(posedge clk) begin
        if(load) begin:init
            for(i = 0 ; i < 16 ; i = i + 1) begin
                for(j = 0 ; j < 16 ; j = j + 1) begin
                    q_2d[i][j]    <=  data[i*16+j];
                end
            end
        end
        else begin:set_val
            for(i = 0 ; i < 16 ; i = i + 1) begin
                for(j = 0 ; j < 16 ; j = j + 1) begin
                    if(nghbr_num[i*16+j] < 2)
                        q_2d[i][j]      <=  1'b0;
                    else if (nghbr_num[i*16+j] > 3)
                        q_2d[i][j]      <=  1'b0;
                    else if (nghbr_num[i*16+j] == 3)
                        q_2d[i][j]      <=  1'b1;
                    else
                        q_2d[i][j]      <=  q_2d[i][j];
                end
            end
        end
    end

    //output
    always@(*) begin
        for(i = 0 ; i < 16 ; i = i + 1) begin
            for(j = 0 ; j < 16 ; j = j + 1) begin
                q[i*16+j] = q_2d[i][j];
            end
        end
    end

endmodule

本题笔者采用一分为 2 的思路：

统计矩阵中每个元素的 8 -相邻元素中 1 的个数
根据相邻元素中的 1 的个数，决定元素下一状态的值

使用组合逻辑，采用相加的方式计算相邻元素中 1 的个数，使用一个 256 长的序列来记录每个元素相邻元素中 1 的个数，最大为 8 个，所以每个元素使用 3 bit 来记录。

wire [2:0] nghbr\_num [255:0];

在统计时，需要处理边界绕回的的特殊情况。对于边界上的元素，根据绕回的规则确立边界。需要特殊处理的是第一/最后一行/列。在编写 Verilog 代码时，可以对这几种情况分别确立边界。
因为不想代表显得太冗长，这里引入了 4 个整形变量 idx\_i\_d, idx\_i\_u, idx\_j\_r, idx\_j\_l ，在不同的情况下，来确立四条边界。

idx_i_u = (i == 0) ? i-1+16 :i-1; //up idx
idx_i_d = (i == 15)? i+1-16 :i+1; //down idx
idx_j_l = (j == 0) ? j-1+16 :j-1; //left idx
idx_j_r = (j == 15)? j+1-16 :j+1; //right idx

使用时序逻辑，根据统计的结果，决定下一周期元素的值。
输出最终结果时，将二维信号重新转换为一维信号，Verilog 不支持直接在一维/二维信号之间赋值。
从下一题开始将进入一个漫长的状态机栏目，我们将讨论多道学习状态机的题目。

Problem 118 Simple FSM1 / Fsm1

牛刀小试

图中是一个有两个状态的摩尔型状态机。有一个输入信号与一个输出信号。本题中需要实现图中的状态机，注意复位后状态为 B，复位采用异步复位。

解答与分析

module top_module (
    input clk,
    input in,
    input areset,
    output out
);

        // -----实现状态机
endmodule

这里我们学习标准答案中的表示，采用三段式的写法来描述这个简单的状态机。三段式状态机虽然代码会长一些，但能够更方便地修改，并更清晰地表达状态机的跳变与输出规则。
使用参数来表示每个状态。

    // Give state names and assignments. I'm lazy, so I like to use decimal numbers.
    // It doesn't really matter what assignment is used, as long as they're unique.
    parameter A=0, B=1;
    reg state;        // Ensure state and next are big enough to hold the state encoding.
    reg next;

    // A finite state machine is usually coded in three parts:
    //   State transition logic
    //   State flip-flops
    //   Output logic
    // It is sometimes possible to combine one or more of these blobs of code
    // together, but be careful: Some blobs are combinational circuits, while some
    // are clocked (DFFs).

三段式分别指

状态跳转逻辑
状态触发器实现
输出逻辑

状态跳转逻辑，根据输入信号以及当前状态确定状态的次态。

    // Combinational always block for state transition logic. Given the current state and inputs,
    // what should be next state be?
    // Combinational always block: Use blocking assignments.
    always@(*) begin
    case (state)
        A: next = in ? A : B;
        B: next = in ? B : A;
    endcase
    end

状态触发器实现，在时钟边沿实现状态寄存器的跳变以及状态复位

    // Edge-triggered always block (DFFs) for state flip-flops. Asynchronous reset.
    always @(posedge clk, posedge areset) begin
    if (areset) state <= B;        // Reset to state B
        else state <= next;            // Otherwise, cause the state to transition
    end

输出逻辑，根据当前状态实现输出

    // Combinational output logic. In this problem, an assign statement is the simplest.
    // In more complex circuits, a combinational always block may be more suitable.
    assign out = (state==B);

Problem 119 Simple FSM1 / Fsm1s

牛刀小试

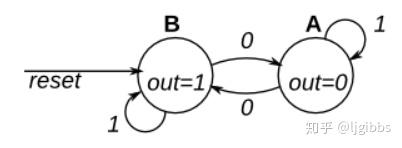
实现一个和上一题相同，但采用同步复位的状态机。

和上一题只是复位的方式不同，这里不再赘述实现代码了。

HDLBits：在线学习 Verilog （二十四 · Problem 115-119）

Problem 115 Rule90

Problem 116 Rule110

Problem 117 Conwaylift/conway's game of life 16x16

Problem 118 Simple FSM1 / Fsm1

Problem 119 Simple FSM1 / Fsm1s

推荐阅读

推荐阅读

目录