文章转载于微信公众号:GiantPandaCV
作者:史开杰
【GiantPandaCV导语】在CNN的训练中,权重初始化是一个比较关键的点。好的权重初始化可以让网络的训练过程更加稳定和高效。本文为大家介绍了kaiming初始化以及详细的推导过程,希望可以让大家更好的理解CNN初始化。
1.为什么需要好的权重初始化
网络训练的过程中, 容易出现梯度消失(梯度特别的接近0)和梯度爆炸(梯度特别的大)的情况,导致大部分反向传播得到的梯度不起作用或者起反作用. 研究人员希望能够有一种好的权重初始化方法: 让网络前向传播或者反向传播的时候, 卷积的输出和前传的梯度比较稳定. 合理的方差既保证了数值一定的不同, 又保证了数值一定的稳定.(通过卷积权重的合理初始化, 让计算过程中的数值分布稳定)
2.kaiming初始化的两个方法
2.1先来个结论
- 前向传播的时候, 每一层的卷积计算结果的方差为1.
- 反向传播的时候, 每一 层的继续往前传的梯度方差为1(因为每层会有两个梯度的计算, 一个用来更新当前层的权重, 一个继续传播, 用于前面层的梯度的计算.)
2.2再来个源码
方差的计算需要两个值:gain和fan. gain值由激活函数决定. fan值由权重参数的数量和传播的方向决定. fan\_in表示前向传播, fan\_out表示反向传播.
`def kaiming_normal_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu'):
fan = _calculate_correct_fan(tensor, mode)
# 通过mode判断是前向传播还是反向传播, 生成不同的一个fan值.
gain = calculate_gain(nonlinearity, a)
# 通过判断是哪种激活函数生成一个gain值
std = gain / math.sqrt(fan) # 通过fan值和gain值进行标准差的计算
with torch.no_grad():
return tensor.normal_(0, std)
`
下面的代码根据网络设计时卷积权重的形状和前向传播还是反向传播, 进行fan值的计算.
`def _calculate_fan_in_and_fan_out(tensor):
dimensions = tensor.dim() # 返回的是维度
if dimensions < 2:
raise ValueError("Fan in and fan out can not be computed for tensor with fewer than 2 dimensions")
if dimensions == 2: # Linear
fan_in = tensor.size(1)
fan_out = tensor.size(0)
else:
num_input_fmaps = tensor.size(1) # 卷积的输入通道大小
num_output_fmaps = tensor.size(0) # 卷积的输出通道大小
receptive_field_size = 1
if tensor.dim() > 2:
receptive_field_size = tensor0.numel() # 卷积核的大小:k*k
fan_in = num_input_fmaps receptive_field_size # 输入通道数量卷积核的大小. 用于前向传播
fan_out = num_output_fmaps receptive_field_size # 输出通道数量卷积核的大小. 用于反向传播
return fan_in, fan_out
def _calculate_correct_fan(tensor, mode):
mode = mode.lower()
valid_modes = ['fan_in', 'fan_out']
if mode not in valid_modes:
raise ValueError("Mode {} not supported, please use one of {}".format(mode, valid_modes))
fan_in, fan_out = _calculate_fan_in_and_fan_out(tensor)
return fan_in if mode == 'fan_in' else fan_out
`
下面是通过不同的激活函数返回一个gain值, 当然也说明了是recommend. 可以自己修改.
``def calculate_gain(nonlinearity, param=None):
r"""Return the recommended gain value for the given nonlinearity function.
The values are as follows:
================= ====================================================
nonlinearity gain
================= ====================================================
Linear / Identity :math:1
Conv{1,2,3}D :math:1
Sigmoid :math:1
Tanh :math:\frac{5}{3}
ReLU :math:\sqrt{2}
Leaky Relu :math:\sqrt{\frac{2}{1 + \text{negative\_slope}^2}}
================= ====================================================
Args:
nonlinearity: the non-linear function (nn.functional name)
param: optional parameter for the non-linear function
Examples:
>>> gain = nn.init.calculate_gain('leaky_relu', 0.2) # leaky_relu with negative_slope=0.2
"""
linear_fns = ['linear', 'conv1d', 'conv2d', 'conv3d', 'conv_transpose1d', 'conv_transpose2d', 'conv_transpose3d']
if nonlinearity in linear_fns or nonlinearity == 'sigmoid':
return 1
elif nonlinearity == 'tanh':
return 5.0 / 3
elif nonlinearity == 'relu':
return math.sqrt(2.0)
elif nonlinearity == 'leaky_relu':
if param is None:
negative_slope = 0.01
elif not isinstance(param, bool) and isinstance(param, int) or isinstance(param, float):
# True/False are instances of int, hence check above
negative_slope = param
else:
raise ValueError("negative_slope {} not a valid number".format(param))
return math.sqrt(2.0 / (1 + negative_slope ** 2))
else:
raise ValueError("Unsupported nonlinearity {}".format(nonlinearity))
``
下面是kaiming初始化均匀分布的计算. 为啥还有个均匀分布? 权重初始化推导的只是一个方差, 并没有限定是正态分布, 均匀分布也是有方差的, 并且均值为0的时候, 可以通过方差算出均匀分布的最小值和最大值.
`def kaiming_uniform_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu'):
fan = _calculate_correct_fan(tensor, mode)
gain = calculate_gain(nonlinearity, a)
std = gain / math.sqrt(fan)
bound = math.sqrt(3.0) * std # Calculate uniform bounds from standard deviation
with torch.no_grad():
return tensor.uniform_(-bound, bound)
`
3.推导的先验知识
3.1用变量来看待问题
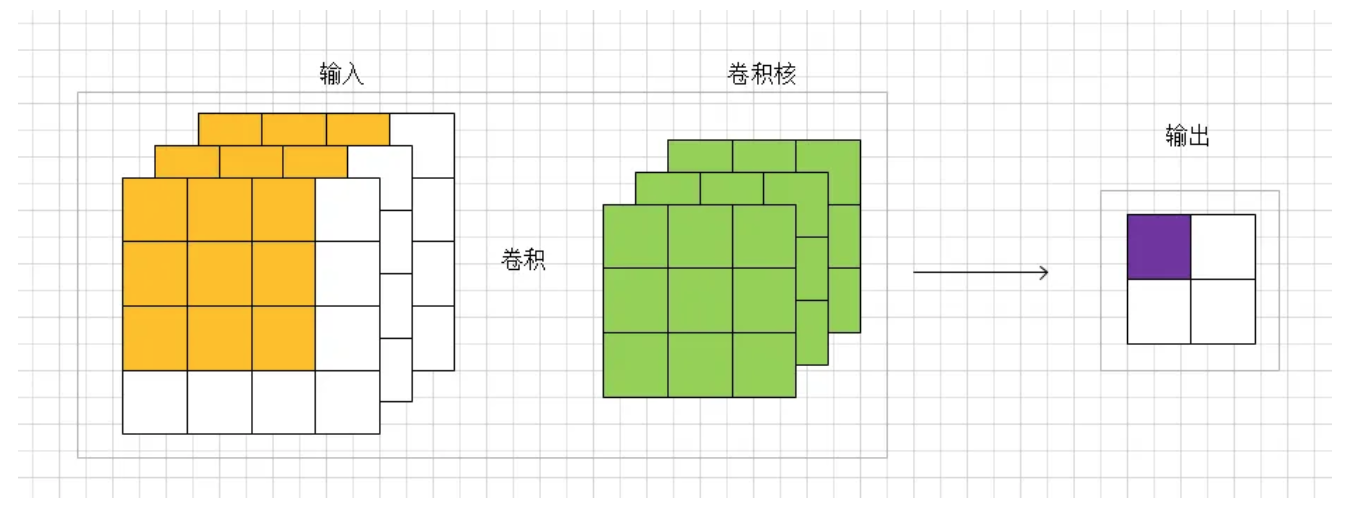
参照上面的卷积图, 对输入的特征图进行的卷积. 具体要研究的是输出的一个点的方差(紫色点). 所以是通过黄色的输入(个)和绿色的卷积参数(个)去计算一个输出值(紫色输出)的方差. 一个点对应于原论文里面的说法为a response. 感觉这个是理解权重初始化的重点. 基于独立同分布的强假设: 输入的每个值都是独立同分布的, 所以和独立同分布的参数进行卷积得到结果的分布也是相同的. 所以其他的3个输出点的方差也是一样的. 进一步说, 虽然输入是个不同的值. 但是我们可以这样认为: 有一个满足某分布的随机变量, 然后随机抽样48次, 这48个值就可以组成了输入, 且独立同分布(也可称输入的每个像素点是独立同分布的). 卷积的参数也可以这么认为. 那么我们可以用一个随机变量表示48个输入, 也可以用一个随机变量表示27个卷积参数, 亦可以用一个随机变量表示4个输出值.
3.2几个公式
4.kaiming初始化
4.1前向传播时每层的方差都是1
4.2反向传播时梯度的方差都是1
推荐阅读
更多嵌入式AI技术干货请关注嵌入式AI专栏。