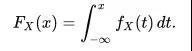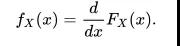论STA：SOCV / POCV 开篇

题记：继续STA 部分的陈诉，跟本篇相关的文章请看《绿蚁新醅酒，红泥小火炉：STA之OCV》《晚来天欲雪，能饮一杯无：STA之AOCV》，POCV 相对来说要复杂一点，期望可以用几篇说得明白。

工艺偏差自集成电路诞生之日起，就是一个无法规避的因素，芯片制造过程不比生个娃简单，且每一个过程都极其精细，即使极尽所能地控制制造过程的偏差，但随着工艺进步，工艺偏差对芯片性能的影响却日渐凸现。为了模拟工艺偏差对芯片性能的影响，引入了On chip variation模型，40nm 之前简单的flat derate模型基本可以覆盖大部分情况，且不过于悲观到不能接受。

但进入40 nm 之后flat derate 已不再是一个『经济』的模型，所以引入了更复杂的AOCV (Advanced OCV) 模型，考虑depth 跟 distance的影响，此时AOCV table的背后已有『统计学』的支撑，即所谓的SSTA (statistical staic timing analysis). 但限于runtime 当今STA 默认都是基于GBA (Graph Based Analysis) 进行timing 分析，这就使得Depth 的计算并不精确，从而导致过于悲观，如果用PBA (Path Based Analysis) 方式来计算Depth runtime又不能接受。

于是进入16nm 之后，一种新的OCV 模型开始被广泛使用，C家称之为SOCV (statistical OCV), S家称之为POCV (Parametric OCV), 除了名字的差别，背后都是统计学都是正态分布，背后的算法也基本一致。因为SOCV / POCV 不再是简单的设一个derate 值或查一个表格，而是要做一系列计算，正是因为这看似复杂的一系列计算，经常让习惯于查表的老硅农晕头转向。其实这就是概率论中最基本的一些概念跟计算，难道你们忘了当年高分拿下概率论这事儿了吗？

概率论中涉及到的随机变量分离散随机变量和连续随机变量，芯片制造过程中的工艺偏差属于连续随机变量范畴，所以在进入SOCV / POCV 之前，先来捋清除几个概念：随机变量、概率函数、累积分布函数、概率密度函数、均值、方差。温习了这些概念之后，再看SOCV / POCV 一切只是套公式，并没想象中那么庞大复杂。

随机变量 (Random Variable)：在现实世界中，许多量是无法准确预测的，故经常使用随机变量来表示。在学数字集成电路时，涉及最多的一个跟随机变量相关的概念应该是管子的阈值电压。

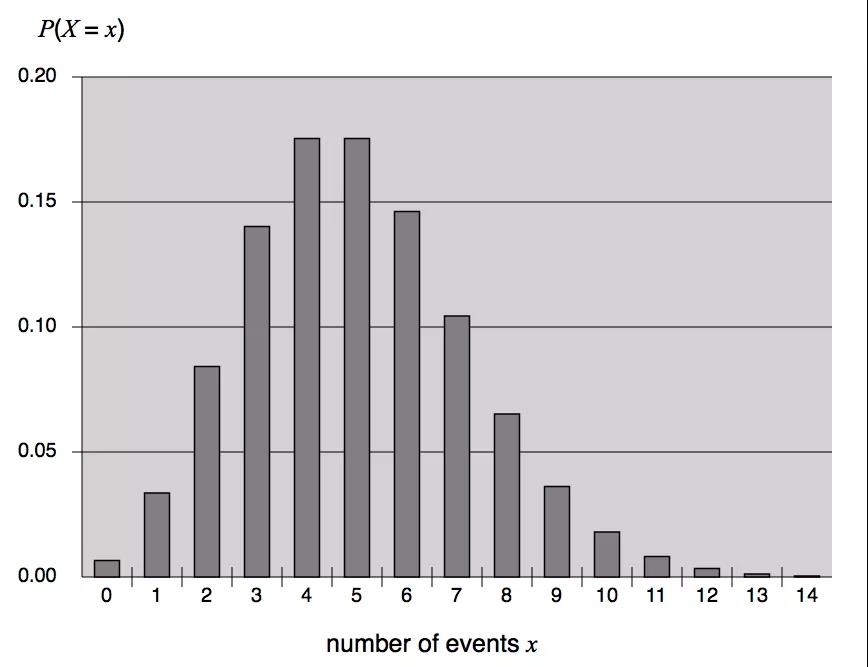
概率函数 (Probability)：如果运行大量测试，会发现随机变量的值通常遵循一定规律。随机变量处于x的可能性称为概率，通常用P(x) 表示。

累积分布函数(Cumulative Distribution Function)：又叫分布函数，用于描述一个实随机变量X的概率分布，是概率密度函数的积分。它就是概率函数取值的累加结果。

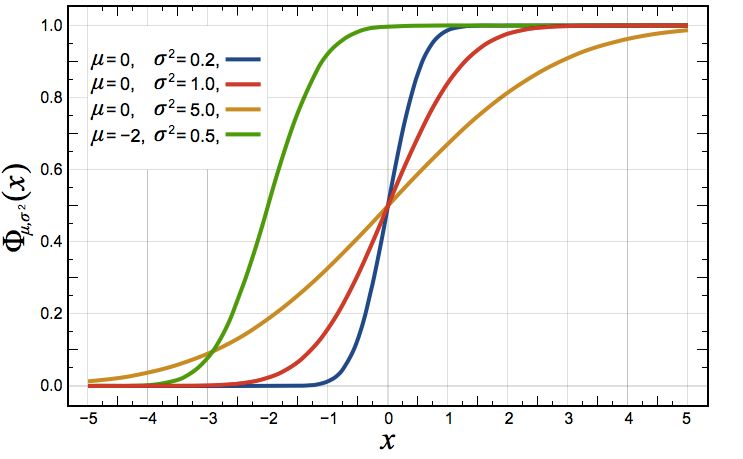
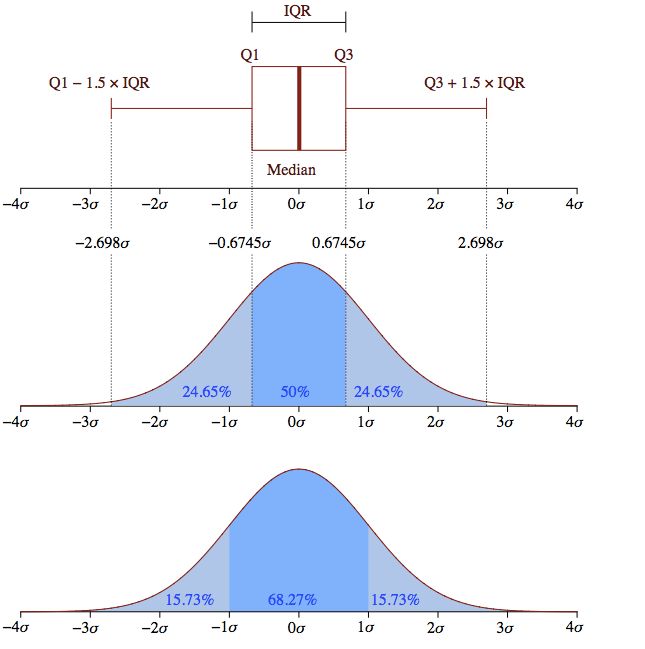
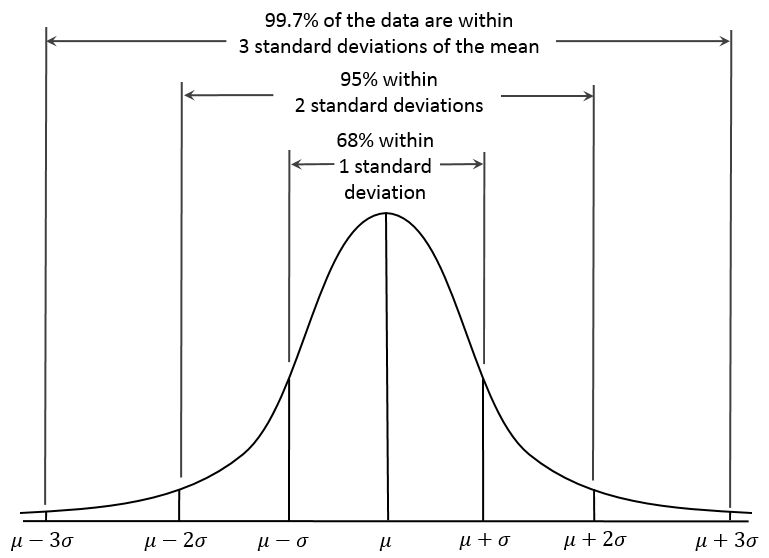
概率密度函数 (ProbabilityDensity Function)：用于描述随机变量落在特定值范围内的概率，这个概率为概率密度函数在这个区域上的积分。如下图，该随机变量落在-1σ \~ 1σ间的概率是68.27%。SOCV / POCV 中sigma的取值，就是根据这个概率得来，所取sigma 的值需要保证大部分情况可以被覆盖到。

均值 (mean)：用于表示概率分布或以该分布为特征的随机变量的集中趋势的一种度量。是随机试验在同样的机会下重复多次的结果计算出的等同“期望”的平均值。

方差 (Sigma σ)：用于描述随机变量与平均值的偏差程度。方差在统计描述和概率分布中各有不同的定义，并有不同的公式。在统计描述中，方差用来计算每一个变量（观察值）与总体均数之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。

正态分布 (Normal distribution) 也称高斯分布 (Gaussian distribution); 对于正态分布，随机变量落在-1σ \~ 1σ间的概率是68.27%，落在-2σ \~ 2σ间的概率是95.45%，落在-3σ \~ 3σ间的概率是99.73%。这也是为什么SOCV / POCV 取3σ 的原因所在。

跋：SOCV / POCV就是一个基于正态分布的OCV 模型，本篇先捋基本概念，概念清除了之后再细看这一模型在STA 中的应用。

作者：陌上风骑驴
来源：https://mp.weixin.qq.com/s/qi0ExFP2B9Au0qDUVK7E9Q
作者微信公众号

相关文章推荐

• 论功耗 | 如何计算toggle rate
• 述职场 | C 记三周年记

更多IC设计技术干货请关注IC设计技术专栏。