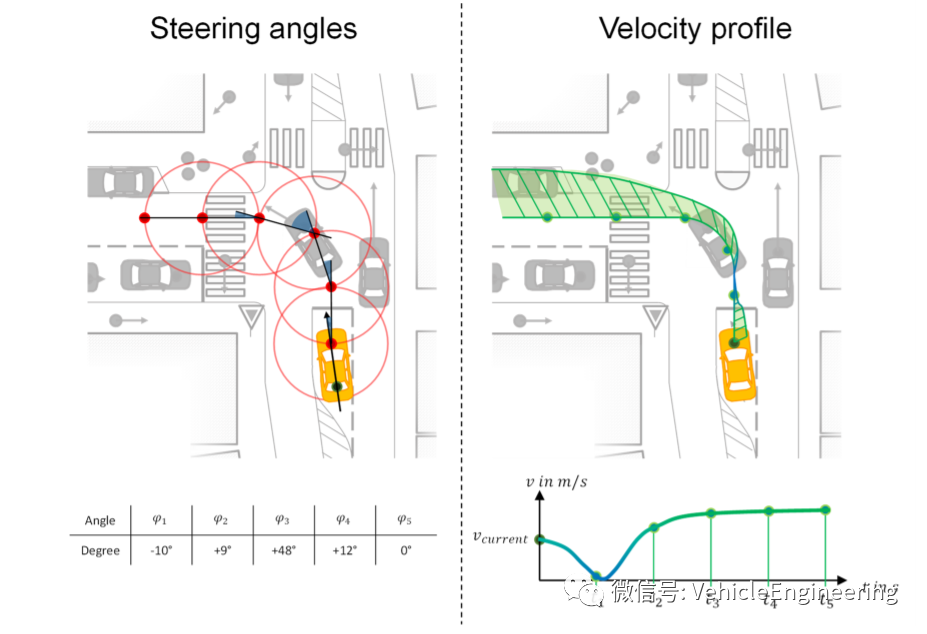
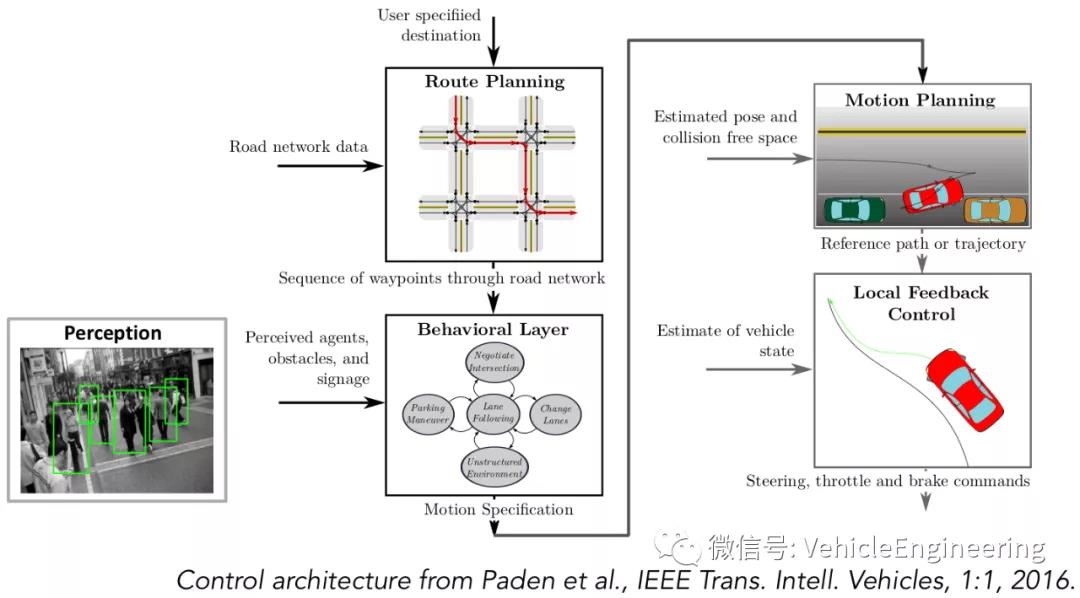
自动驾驶在找到要遵循的最佳路径(自动驾驶实时路径规划算法简介(RRT 和Lattice Planner))和进行的最佳操纵(自动驾驶机动动作规划和决策)之后,必须生成满足运动模型或状态约束的轨迹,并保证乘客的舒适性和旅途的平稳性。根据所选择的路径和机动动作,生成轨迹的问题主要通过选择一条几何曲线来解决,以保证在道路网络中的平稳运动。然后根据动态模型和/或该轨迹上是否存在障碍物,使用成本函数对该轨迹进行优化。
本文将介绍几种轨迹生成算法和方法
轨迹的几何表示包括圆弧(如Sun等人,2014)、回旋体(如Broggi等人,2012)、纳尔逊多项式(如Xiu和chen,2010)、多项式缓和曲线(如McNaughton等人,2011;Gu等人,2013)、样条曲线(如Wang等人,2011;Hardy和Campbell,2013;Kala和Warwick,2013)和Bezier曲线(例如。Zhao等人,2011年;Ma等人,2012年)。
在这类规划问题中,所使用的几何曲线仅限于某种类型(如样条曲线、Bezier曲线、多项式或回旋曲面),并通过求解每个时刻的两点边值问题来构造分段路径。
Delsart等人(2009)提出了一种轨迹生成算法(TiJi),该算法根据当前状态与最终状态之间的误差对二阶多项式轨迹进行优化。采用包含二维位置、方位、转向角和速度的车辆模型,计算每个点的速度和加速度分布。当收敛点远离最终状态时,不考虑障碍物,计算复杂度增加。
Sawodny等人。(2010)使用四阶多项式和具有平坦性的动态单车模型9来描述车辆的运动。约束适用于车辆的最大加速度和最大驱动力。该方法还考虑了超车和跟车情况,每种情况下的成本函数不同,基于对向车道上车辆存在的概率和安全距离约束。在模拟实验中,假设车辆采用恒定速度;这可能不适用于实际情况。
Ma等人提出了一种更平滑、更可控的轨迹。(2012),作者使用三次贝塞尔曲线进行轨迹规划。它们的成本函数包括轨迹长度、平滑度和与用作参考路径的车道中心线的偏移量的权重。障碍物被视为圆形,并通过碰撞轨迹进行碰撞检查,这可能导致过度计算。Perez等人(2013)中也使用了10立方贝塞尔曲线来生成环形交叉路口情况下自主车辆的轨迹;但是,碰撞检查、侧向加速度和曲率约束被省略。
Bae等人提出的三阶和五阶Bezier曲线在变道机动中的比较。(2013)表明,五阶曲线为动态道路环境构建了更平滑、更可行的路径。该方法使用小型车辆进行测试,但在这种测试中不考虑实际车辆动力学(什么是车辆动力学点击干货 | 整车敏捷性Agility 开发101)。
冈萨雷斯等人使用四阶贝塞尔曲线来获得更好的结果。(2014年)。除了反映路径规划者指示的路径的车道约束外,还考虑了道路约束。如果存在障碍物,这项工作还包括曲线的变形。虽然在舒适性问题上对速度和加速度进行了限制,但作者假设速度较低,只考虑静态障碍物。
Wang等人提出了一种更完整的方法,即考虑的操纵和交通规则。(2011),其中Akima样条插值用于生成符合路径规划模块、停车标志、红绿灯、转弯、车道变更、交叉口、让路标志、反向行驶和死角的检查点的轨迹。根据到达下一个检查点的距离和时间以及与障碍物的碰撞来评估轨迹。演示是在模拟环境和真实世界的车辆中演示的,并且声称对于真实世界的自动驾驶来说已经足够了,尽管没有提供大量的结果。
Gu and Dolan (2014) 开始学习人类驾驶轨迹模式,并应用于在线轨迹生成。用样条曲线表示轨迹,以便在上级规划模块给出的航路点之间进行插值。轨迹受曲率、速度和加速度的限制。然而,环境应该是没有交通的,法规或天气状况等外部因素都没有考虑在内;更不用说,必须使用大量的自然驾驶数据来学习人类驾驶模式。
宝马自主车Bertha的轨迹规划在驾驶通道内进行,这限制了车辆的行动空间(Ziegler等人,2014a)。成本函数的权重与原始路径的偏移量、速度和加速度以及车辆的期望性能有关。此外,车辆的运动学和动力学约束了给定轨迹的曲率和轮胎的允许摩擦力。当新的信息到达传感器时,通过圆近似来考虑障碍物,并遵循重新规划方案。主要缺点是计算复杂性(对于驾驶走廊的构建)和该方法的普遍适用性。
轨迹规划的另一种方法是模型预测控制(MPC),它结合了规划模块中控制工程的各个方面。在MPC中,使用了车辆的动态模型,并通过该模型,对来自控制器的输入进行采样,以了解车辆运动的未来演变。根据动力学模型和控制器输入,解决了车辆最优轨迹的寻优问题。MPC在Madas等人的驾驶走廊内使用。(2013)使用具有线性轮胎特性的线性自行车模型,该模型还考虑了横向和偏航动力学。推导了预测和控制范围、侧滑角和转向角、转向角速率和横向位置的约束条件。结果表明,侧向加速度较小;因此,对潜在乘客来说更舒适,但与样条法和格点法相比,它需要更大的挺力。该技术的一个弱点在于,用于建模车辆的变量越多,优化其轨迹就越困难。然而,由于它是在行车走廊内进行的,因此它更适用于结构化领域(如高速公路),其性能不依赖于障碍物数量的增加或减少。
Li等人也提出了MPC轨迹方法。(2014)使用参考路径和车辆模型,描述其位置坐标、航向和路径曲率。采用三次样条函数表示轨迹,通过优化到障碍物的距离、与参考路径的距离、轨迹平滑度和前瞻距离的函数来选择最佳轨迹。除了MPC对所考虑变量的敏感性外,上述工作仅用于静态避障。
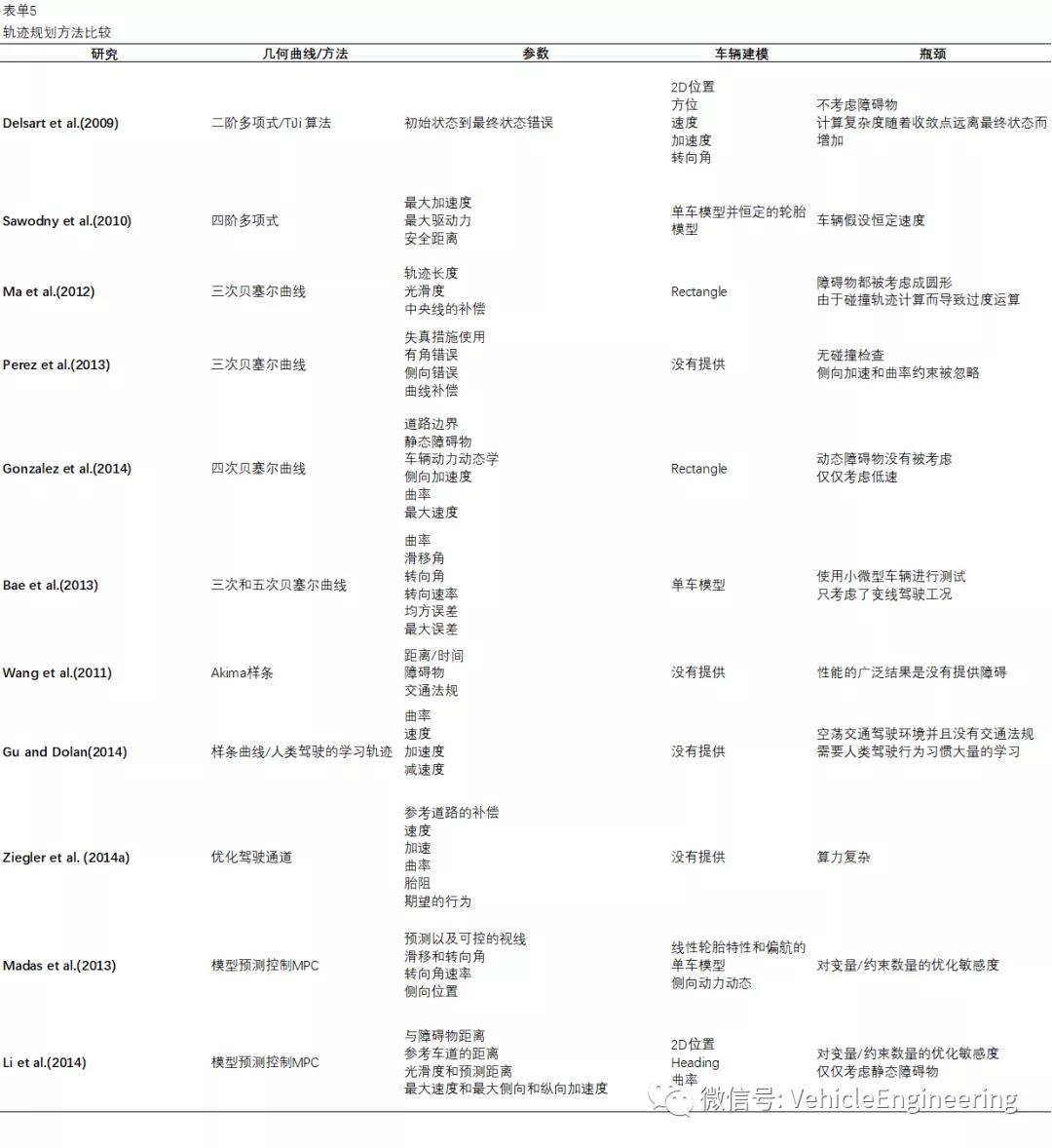
轨迹规划方法在表5中进行了比较
综上所述,可以得出这样的结论:在最低层次的规划中,给定较高层次的路径和行为,最终的轨迹是在每个时间段制定的。然后根据实时运动学和运动模型约束以及道路上障碍物的位置对几何曲线进行优化。曲线的选择通常与路径的平滑度和曲率、它为乘客提供的舒适度以及用于建模车辆的动态方法和计算时间有关。
自动驾驶规划方法的总结
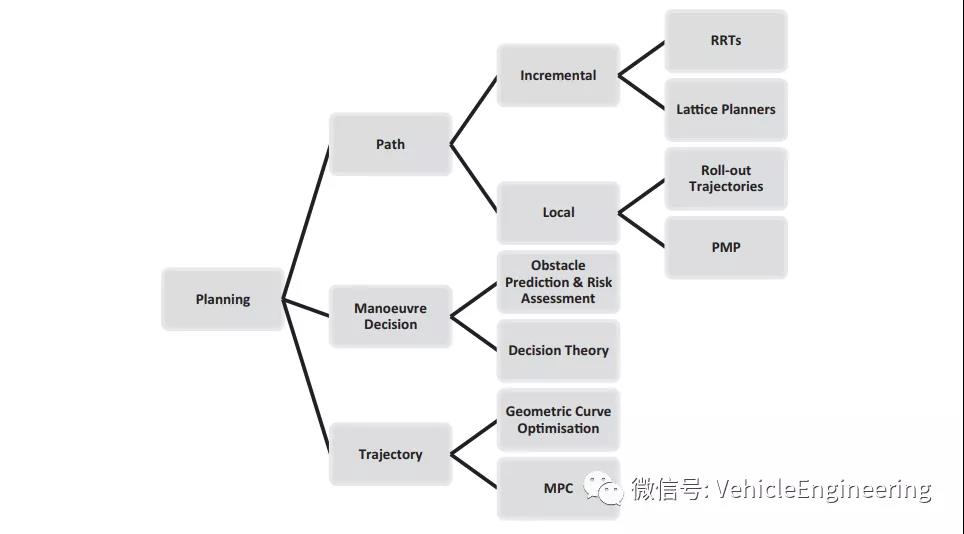
如前所述,自动驾驶车辆的规划可分为三个主要层次:
搜索最佳路径、
搜索最佳机动动作,
搜索最佳轨迹。
寻找最佳路径可以进一步分为寻找朝向目标的最佳路径序列和在有限的“局部”时间和空间范围内搜索。
在机动规划方面,障碍物预测和风险评估被应用,而决策理论方法(如马尔可夫决策过程和博弈论)最近出现,以解释交通环境中的相互作用。
最后,在轨迹规划中,所选的几何路径受运动学和运动模型约束,并进一步优化,以保证沿该路径的平稳可行。这种优化要么基于几何曲线来表示路径,要么基于模型预测控制。
上图总结了这些方法及其子类。应注意的是,在当前的研究中,这些方法很少被单独处理;相反,它们通常被组合起来,以便为车辆提供一个完整的计划。
参考文献:
1,Real-time motion planning methods for autonomous on-road driving: State-of-the-art and future research directions -Christos Katrakazas a , Mohammed Quddus a,⇑ , Wen-Hua Chen b,1 , Lipika Deka a
2,Partial Motion Planning Framework for Reactive Planning Within Dynamic Environments
3,AI-based movement planning for autonomous and teleoperated vehicles including the development of a simulation environment and an intelligent agent
文中部分图片版权归其所有
*未经准许严禁转载和摘录
作者:Pirate Jack
来源:https://mp.weixin.qq.com/s/fWFDw\_oMxu6G0i7jGyGT5Q
Vehicle微信公众号
相关文章推荐
更多汽车行业干货请关注Vehicle专栏。