接上篇,在3月25日的MegEngine Meetup中,旷视研究院周亦庄讲师分享了《利用 MegEngine 分布式通信算子实现复杂的并行训练》。
分享内容主要分为四个部分:
1、 介绍 MegEngine 的分布式通信算子;
2、 简单参数并行,用于熟悉模型并行的一些基本概念;
3、 层内模型并行;
4、 层间模型并行和流水线并行,同时介绍了如何实现一个简单的 GPipe。
本文为该分享实录的下篇,主要包含:层内模型并行、层间模型并行和流水线并行,以及如何实现简单的GPipe。继续Enjoy~
层内模型并行
层内模型并行在原理上更加复杂。我们刚才讲的参数并行,它其实是一种层内模型并行的一种特例,因为它非常的简单,只需要对参数进行 AllGather。实际上我们的层内模型并行还有多种不一样的实现。
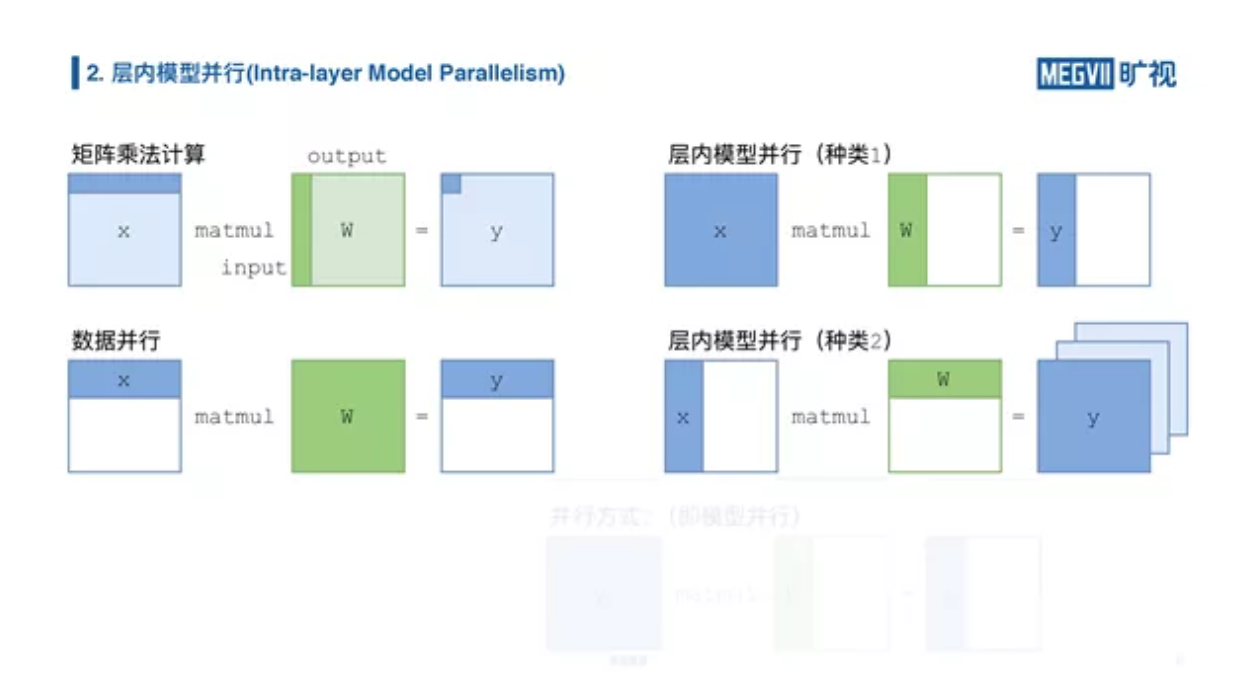
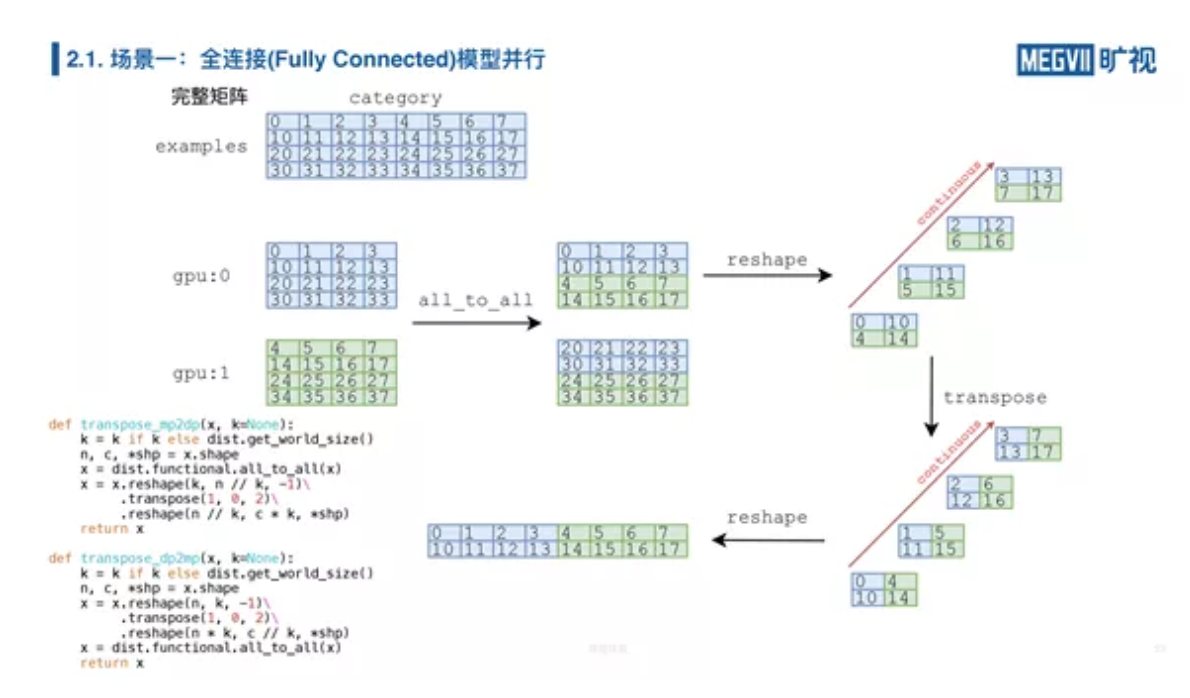
上图给出了完整的矩阵乘法、数据并行和两种模型并行的实现。
我们知道矩阵乘和卷积神经网络中的卷积层(卷积层可以视为对 channel 维度进行的矩阵乘),都天然具有并行的特性。我们在数学意义上的矩阵乘法,每一行每一列的运算都可以独立进行,数据并行就充分的利用了这个特性,我们把数据进行平均切分,各自放在不同的设备上各自做矩阵乘法,最后可以合并起来得到完整结果。
在层内模型并行当中,我们是把每层(全连接/卷积层)的参数矩阵 W 进行切分。一种方式是按输出维度进行切分(纵切)。第二种种类是按输入维度进行切分(横切)。前者在每张卡上得到部分输出维度的对应结果;后者利用了矩阵的低秩特性(Low Rank),每张卡的结果是最终结果的低秩分量,后续须通过 AllReduce 或者 ReduceScatter 将其求和。
接下来我们在多层神经网络中应用层内模型并行——我们实现纯粹的层内模型并行,或者和数据并行搭配使用,完成混合并行。
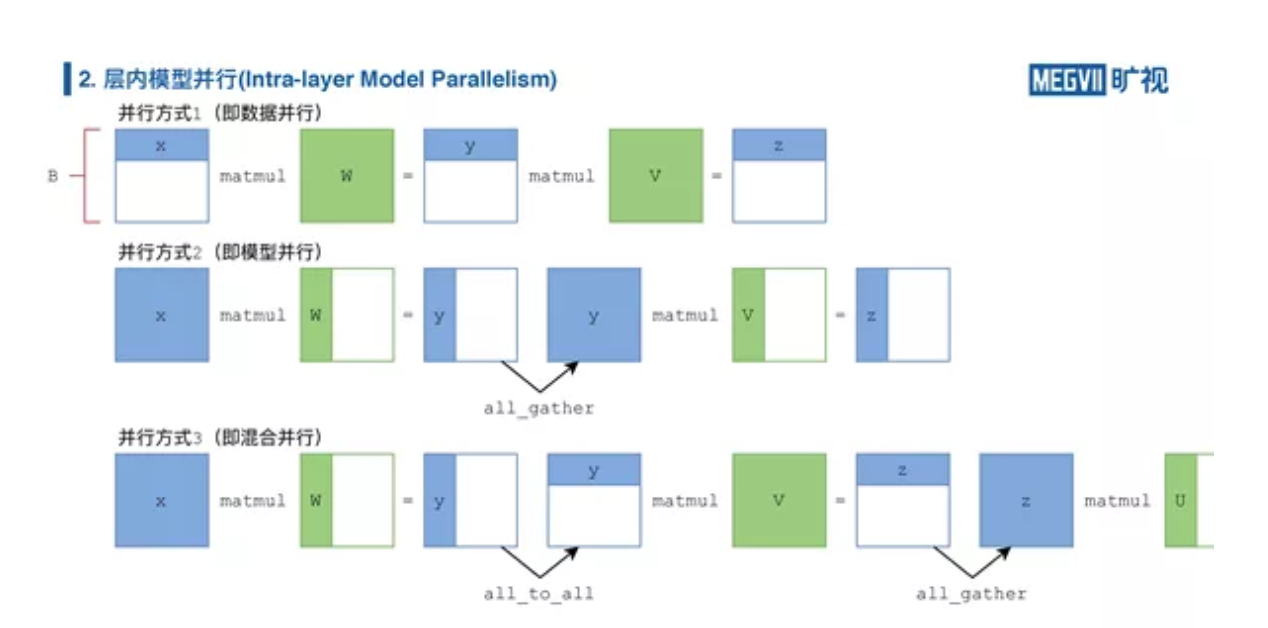
上图第一行是纯数据并行。数据在一开始就被切分到各张卡上,之后不需要进行交换或信息交流,因此数据并行后接数据并行不需要进行特殊操作。
第二种纯层内模型并行。首先你需要完整样本数(batch)的输入特征“X”,最后矩阵乘出来它是完整样本数但部分输出通道数(channel)的特征“Y”,为了后续继续进行模型并行的矩阵乘法,我必须做一次 AllGather,把“Y”沿着通道(channel)收集起来,把它再变成样本数和通道数皆完整的“Y”,再与模型并行的“V”相乘。如果网络继续加深,那么每次矩阵乘结束都要进行 AllGather 操作。
第三种混合并行混合了数据并行与层内模型并行。我们还是以模型并行开始,模型并行的全连接层输出一个纵切的“Y”(即沿输出通道切分的特征 Tensor),但是我们数据并行要的是横切的“Y”(即沿样本数维度切分的特征 Tensor),应该怎么操作?
在介绍 MegEngine 通信算子的时候我们提到一个转置操作叫 AllToAll,它可以直接把这个纵切的“Y”变成了横切的“Y”。接下来我们就可以恢复数据并行了,进行一次数据并行的矩阵乘法后,我们还想进行一次模型并行的矩阵乘法,那就再做一次 AllGather,得到全部样本数且全部通道数的完整特征 Tensor。掌握了利用 AllToAll 和 AllGather 实现的“切换”以后,你就可以自己设计与训练混合并行的模型。
接下来我们举例两个应用场景。
场景一:全连接的层内模型并行
我们来进入一个具体场景,在人脸识别任务中应用全连接的层内模型并行。
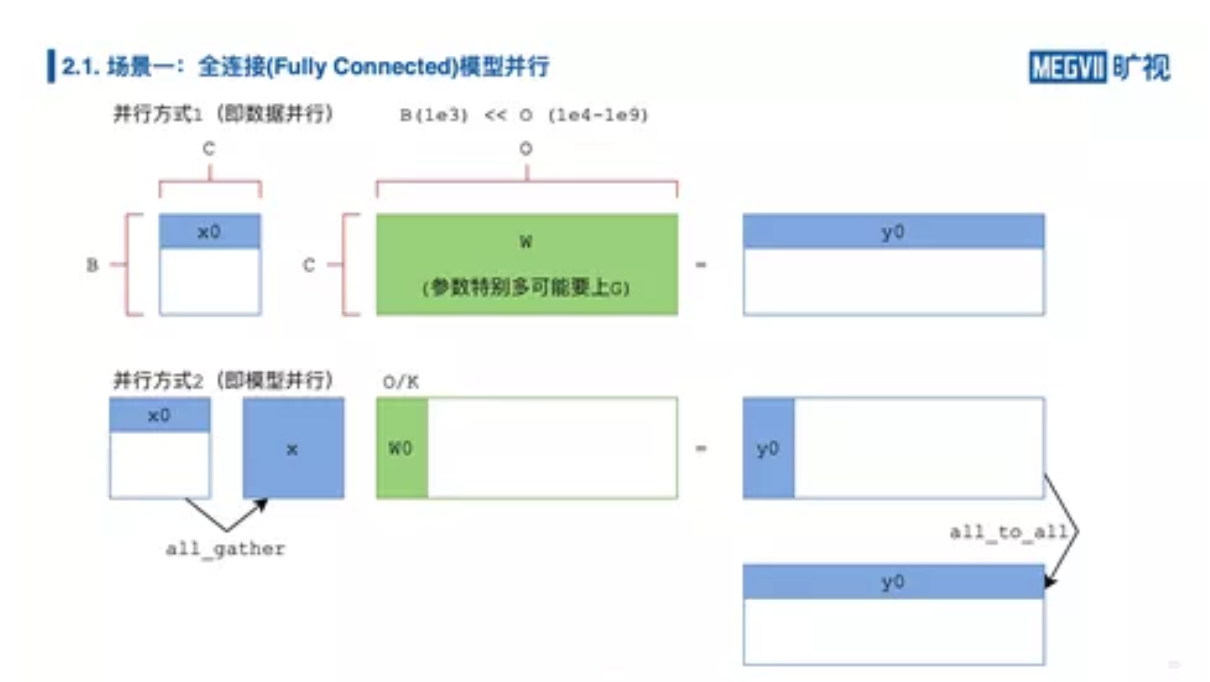
在人脸识别任务当中,可能有百万、千万的 ID(Identity,同一个人为一个 ID),相当于要去做一个输出维度为百万/千万的分类任务,所以,最后这一层,分类的这一层 FC 层(全连接层)它可能参数特别大,比如说我们有一百万(1 million)的 ID,提取的人脸特征是一个 1024 维的向量,它们乘起来就会占用 4 个 G 显存,我们刚才提到 4G 参数的模型在实际训练中会固定占用 3 倍显存,就是 12G,一般的显卡装不下。我只能把这个全连接给放到各张卡上,如果我们有 8 张卡,每张卡就只会分到 1.5G,那么还是可以接受的。这个场景的特点是什么?就是人脸特征维度相比于我的参数矩阵其实非常小的,所以我们对数据进行通信(AllGather),它的代价要比对权重进行通信(AllReduce)它的代价小得多,所以在这个场景下特别适合做模型并行。
在模型并行下分类器 W 输出的结果 Y 的具体含义是什么?我们知道 Y 是竖着切分的,竖着这一维是样本(batch)维,就是它有多少个训练的样本,横着的这一维其实是 ID 维度,就是类别维,表示样本属于各个 ID 的概率,而模型并行下它只输出了一部分标签的概率。求损失函数的时候我们往往用交叉熵(CrossEntropy),交叉熵需要全部的类别概率。没错,利用之前我们介绍的 AllToAll 算子,我们把输出的模型并行的概率矩阵给进行 AllToAll 转置,它就变回了数据并行的格式。(讲师注:实际上你并不需要进行 AllToAll,在分类任务的特殊场景下,你并不需要 AllToAll,因为通信代价很大,你可以籍由两次极低代价的通信来实现交叉熵的计算,但是这个超纲了,但不是很困难,留给大家当思考题。)
我们直接上代码。
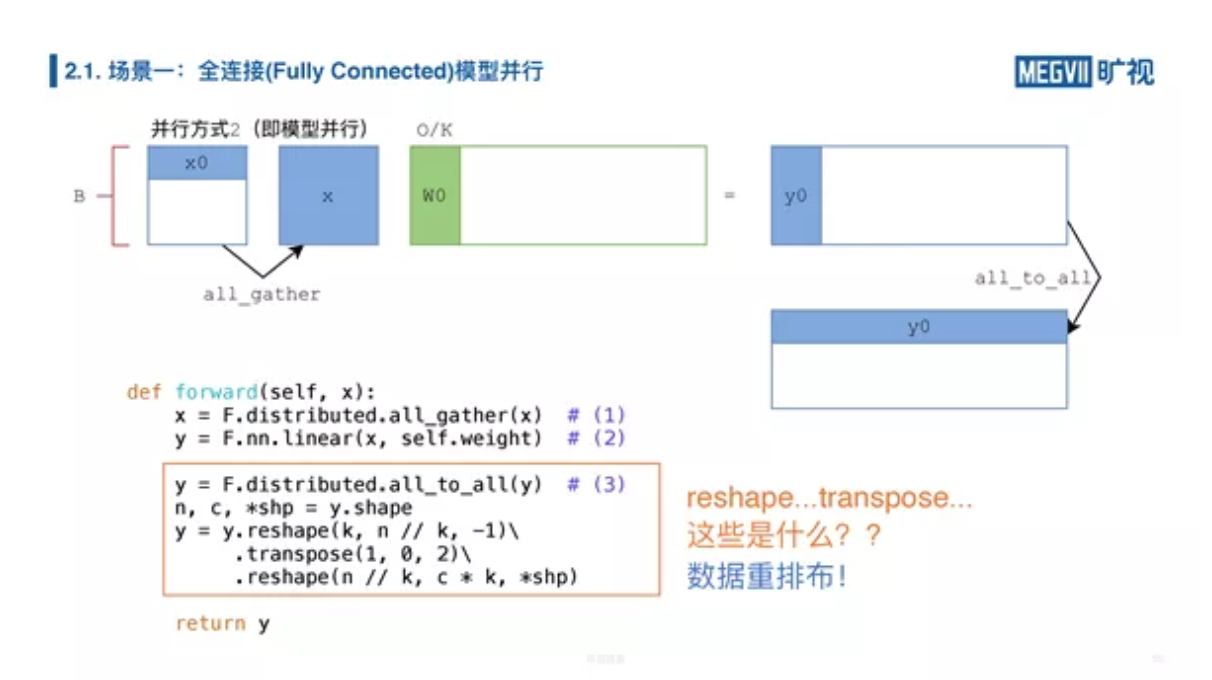
整个过程中有三步,第一步是 AllGather,第二步进行矩阵乘,第三步进行 AllToAll。
那么上图框起来的这段代码是什么东西呢?我们做了这么多 reshape,什么 transpose——这叫数据重排布,我们再花 5 分钟的时间来讲一下数据重排布是什么。
我们 AllToAll 做完以后,得到的其实并不是我们想要的部分数据加上全部分类的一个结果,它其实在底层的数据排布(layout)上面它不是我们期望的。上图是 1 个简化版本的例子,它的分类从 0-7 总共有 8 类,它的样本是 4 张人脸图片。经过模型并行,在卡 0 上面我们得到的输出是 0-3 类的结果,卡 1 上面得到的是 4-7 类的结果。我们做完 AllToAll 以后它变成的矩阵(0,1,2,3,10,11,12,13)并不是我们想要的,我们最后想要的就是 0,1,2,3,4,5,6,7,下面是 10-17,所以的话我们必须先做一次 reshape,沿着这个方向是最里面维 0,1,2,3 数据是连续的,我们把这外面两维(0,10,4,14)个给进行一次转置,就是转过来,最后 reshape 为想要的结果。为了以后使用方便,我简单进行了以下两个封装,上面封装叫 mp2dp,就是从模型并行变成数据并行(Data Parallelism)的一个封装,下面这个是 dp2mp,有了这两个封装以后,我们上面的前传代码就变得简单了。
场景二:组卷积模型并行
讲完了全连接,接下来我们再讲组卷积(Group Convolution)。
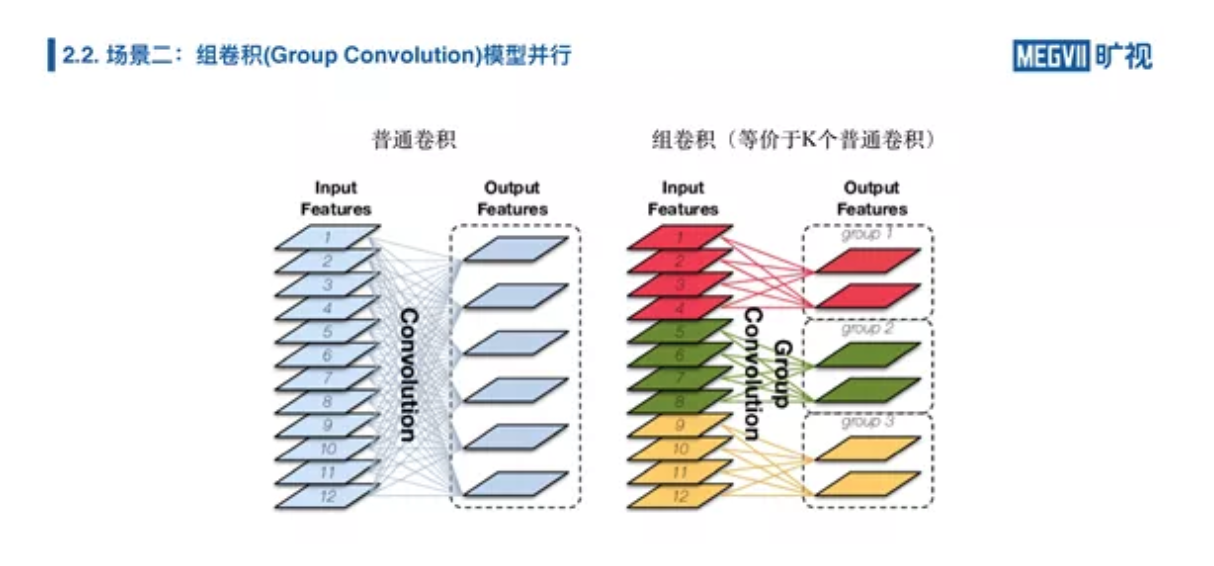
Group Convolution 在我们的移动端模型上面特别常见,组卷积和普通卷积它的区别就在于组卷积相当于 K 个普通卷积。比如说你有三组,就相当于三个普通卷积,但是每个普通卷积都比自己的小,你们也可以发现这个是天然并行的,上图红色的、绿色的、黄色其实可以各自做,在不同的设备上做。
下图用之前二维的表示抽象一下卷积和组卷积的不同——组卷积的模型,它和卷积不一样,组卷积相当于一个稀疏的矩阵乘法,它不是一个稠密的的矩阵(dense matrix)。
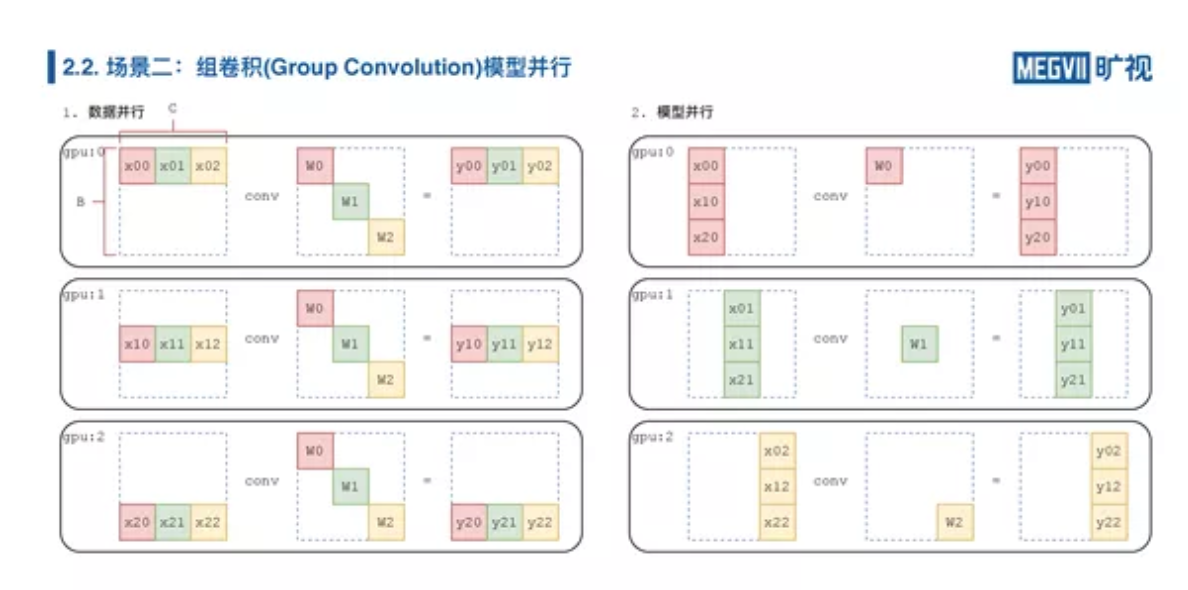
数据并行情况下和普通卷积一样,我们把数据进行切分;模型并行我们可以直接按颜色把这三个组分开,我们第一块卡上做第一个组,第二块卡上做第二个组,第三块卡上做第三个组,对于每块卡来说,原本的组卷积计算都变成了普通的卷积操作。
如果我们前面是普通卷积,中间要插入一组模型并行的组卷积,我们应该怎么样从这两种数据排布之间切换?
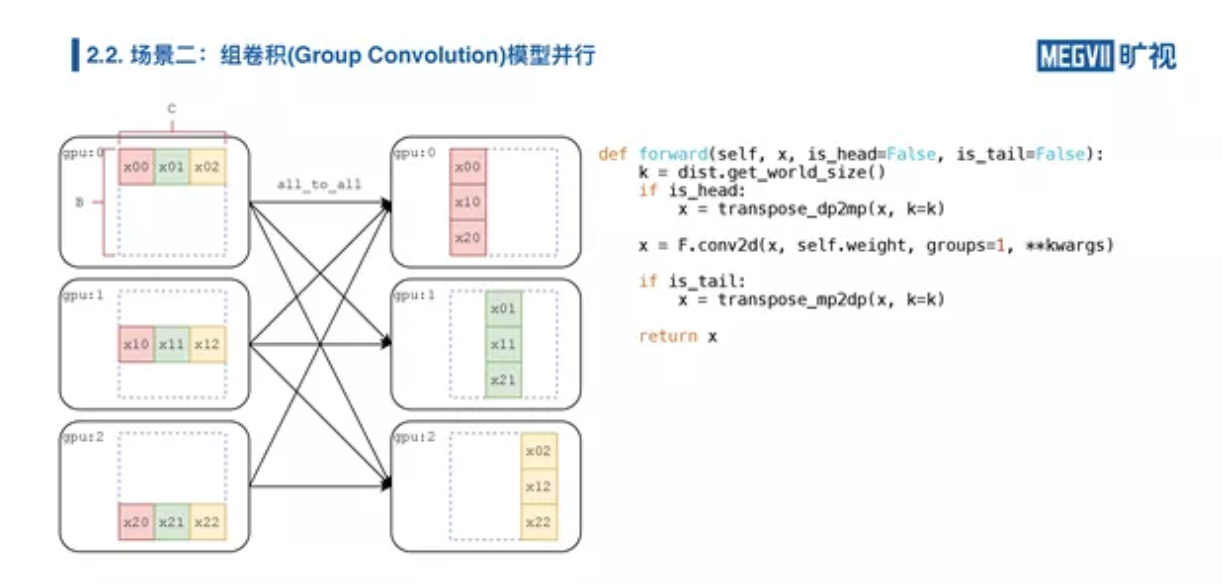
很简单,我们就做一次数据重排布(即 AllToAll),由于是数据并行到模型并行,所以我们调用transpose\_dp2mp。
如果我们有多个组卷积,他们连在一起,实际上我们并不需要反复地在数据和模型并行间切换,我们只需要关注头和尾。所以,我们的组卷积在前传函数里面有一个叫 is\_head 和 is\_tail,我们 is\_head 的时候,我们做一次通信, is\_tail 的时候再做一次通信,我们中间就完全不需要通信了。
层间模型并行
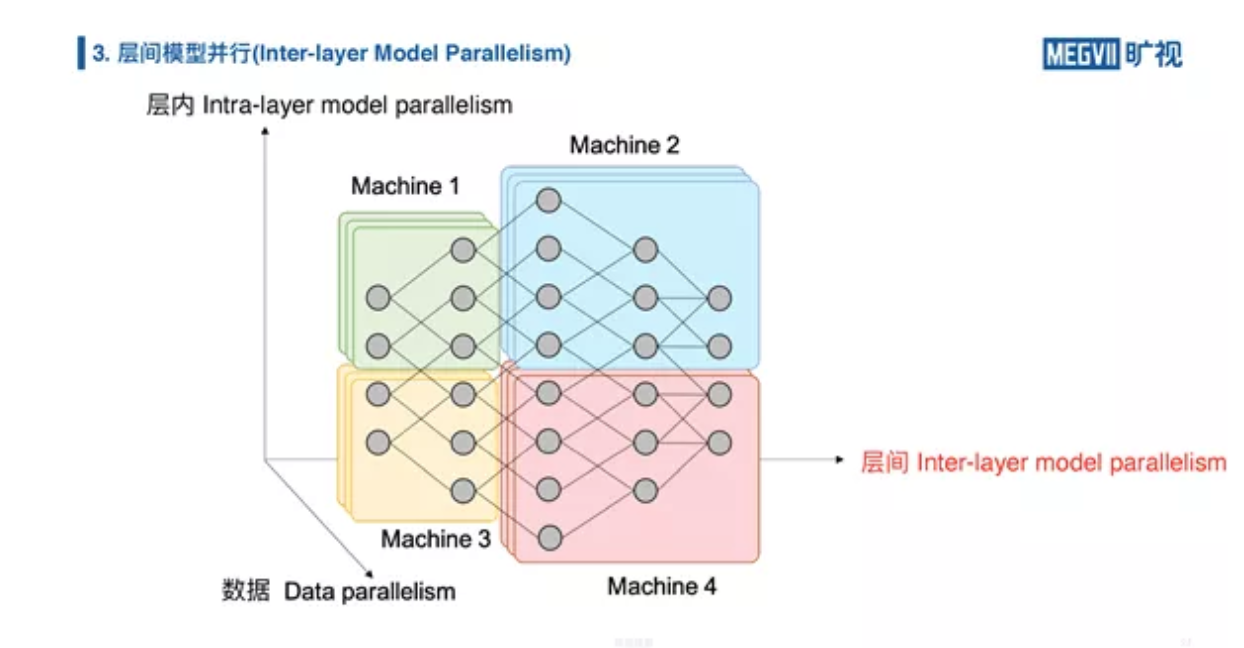
我们进入层间模型并行,刚才的层内模型并行我们介绍了相关原理和应用(全连接和组卷积)。层间模型并行和层内模型并行很不一样,主要就是简单模型并行和流水线并行。层间模型并行简单来说就是把网络的前半部分、中间部分和后半部分分开(甚至分成更多份),就像一条鱼,鱼头、鱼中和鱼尾。
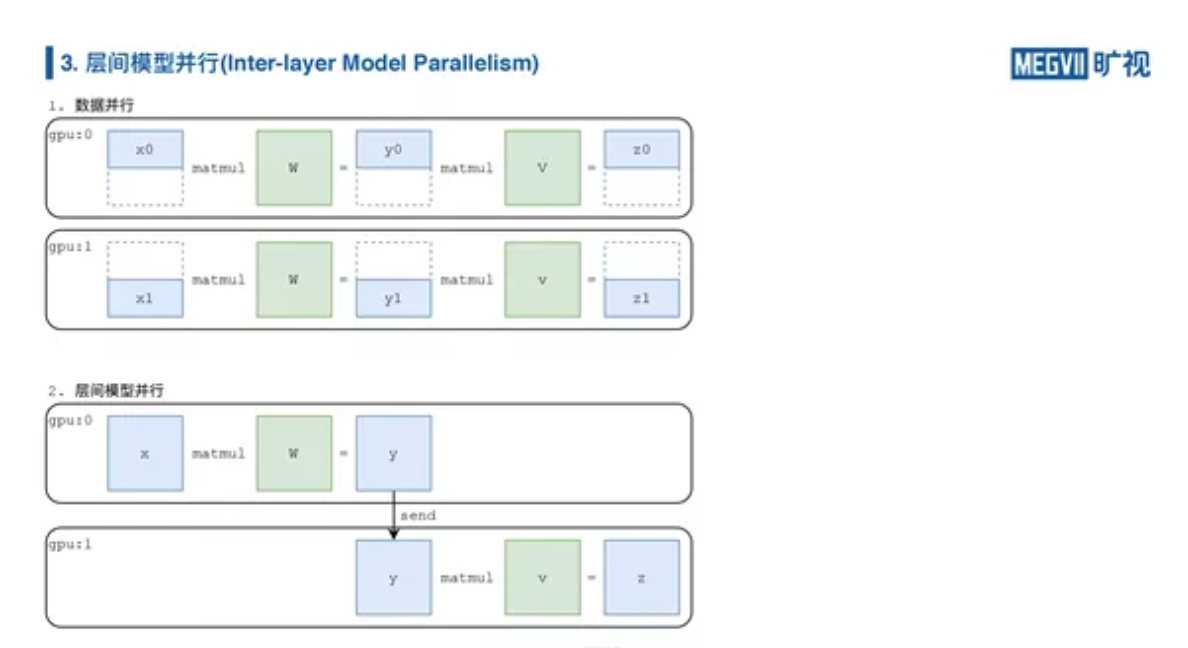
我们简单来看一下数据并行和层间模型并行的对比示意图。
数据并行就是把数据切开,层间模型并行不切数据,而是把模型的前半部分和后半部分给拆分到不同的 GPU 上,这边就涉及到一个问题,怎么把“Y”第一块 GPU 的输出结果,给“放”到第二块 GPU 上,这里面就需要 send 操作。MegEngine 提供了八个集合通信算子,加上两个点对点通信算子——一个就是 send,一个就是 receive。这两个算子组成了层间模型并行的核心操作,接下来主要讲 send receive。
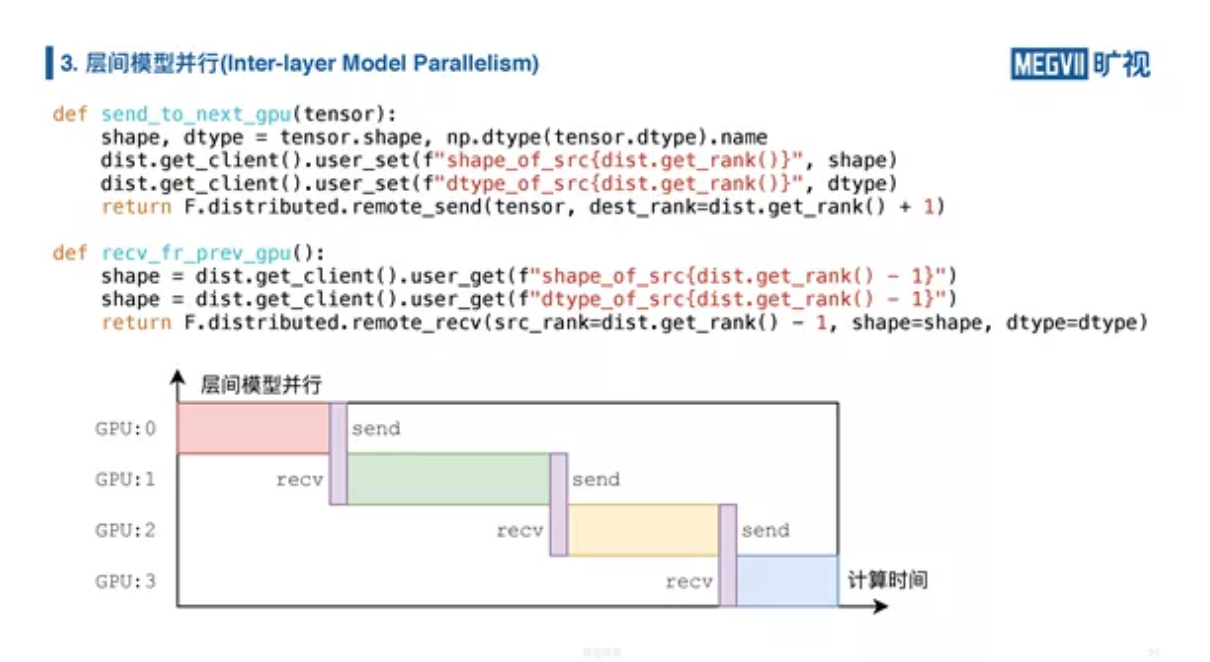
如果层间模型并行,我们用一个图表来抽象的话(如上图下半部分),横轴是计算时间,随着计算推进,纵轴是我们的计算设备(GPU),我们发现任务之间存在依赖关系,所以 GPU 0 算完后必须做 send 操作,同时卡 1 做 receive 接收卡 0 的结果,然后进行自己的计算,算完再 send,卡 2 receive……这样才能做完一个流程。
为了方便起见,我们这边又做了一次封装,第一个函数是把我们出来的计算结果给发到下一个 GPU,这个函数是下一块 CPU 调用的,就是它从上一个 GPU 去给它拿出去,MegEngine 自带的 recv 不带自动的形状和类型推导(讲师注:在 MegEngine 的下个版本即将支持),因此封装的时候我也简单实现了一下。
简单模型并行
我们直接看代码,在普通的数据并行里面,这是一个简单的 ResNet 18的模型,它总共有 17 层卷积加上一层全连接,在简单模型并行里面,如果它是第 1 块 GPU,它就负责第一部分的 5 层卷积,第2第 3 块各负责 4 层卷积,最后一块 GPU 负责 4 层卷积和最后的一层全链接。
在前传的时候先进行判断——当我们如果不是第 1 块 GPU 的话,我们就从前面一块卡拿数据。之后进行自己负责的卷积计算。得到结果后再次进行判断——如果不是最后一块 GPU,我们要把我的数据给送到下一块 GPU 上,如果是最后一块,就直接 return。
我们可以用代码来展示简单模型并行的推理和训练的结果:
在推理过程中,输入一张组(32张) 224分 辨率的图片,前三块 GPU 输出的都是网络的中间特征,最后的 GPU 输出的是网络的预测值。在训练当中值得一提的:
第一,因为是模型并行,所以我们不需要进行 AllReduce;
第二,前三块 GPU 在调用 gm.backward 时传入了一个 None,其实我们在设计 API 的时候,backward 任何东西都可以,backward None 在这里会发生什么?由于前传有一个 send,所以自动微分的时候就会插入一个 recv,它会先等待来自下游的梯度,然后进行正常的反传。
流水线并行
我们接下来讲流水线并行。简单的模型并行需要算完同一批次的全部的数据再给下一个批次的数据,实际上每一张卡都会有很长时间的空闲期,它要么在等上一块卡跑完,要么完成了自己这一批的任务,在等待下一批次的数据。
如果我们把一个批次的数据给分成很多小份的话,我们可以让第 0 块卡先算一小份,算完以后立马送给下一块卡,然后再计算下一小份,这样子的话这个时刻卡 0 和卡 1 可以同时算,空置率就下去了。
这就是流水线并行的一个核心思想,我们看一下它代码怎么实现。
比如在这个里面,我们想要把一份数据给拆成 4 份,我们用 F.split 将它拆成 4 分,然后遍历一遍这 4 份数据,如果它是第一块卡,它就拿那个数据,不然的话它会等,等着接收前一块卡的计算结果。不管怎么样拿到数据以后的事情就是进行计算,计算完以后我们要处理计算结果——和简单模型并行一样,如果他不是最后一块 GPU,我要把它送到下一块,如果它是最后一块 GPU 的话,就直接出来返回结果。
这就是流水线并行。当然到实际场景中流水线并行的代码需要考虑执行效率,没有这么简单,比如说会引入异步 send/recv,以降低等待时间。
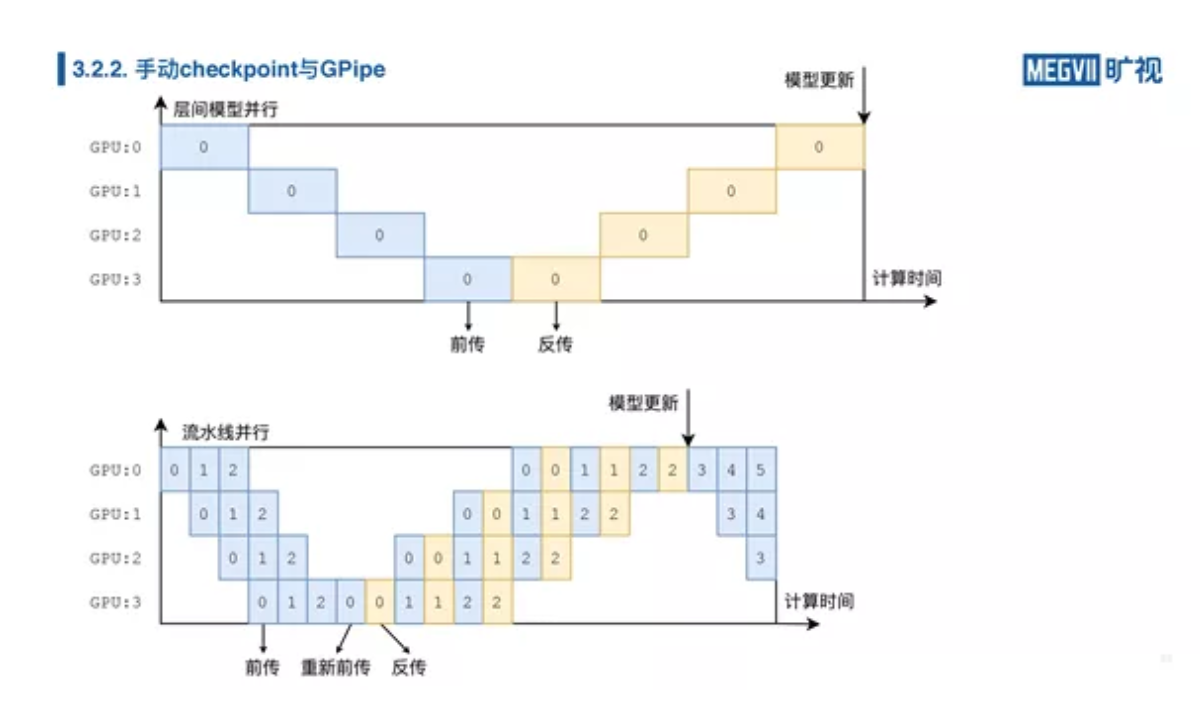
我们不光要推理,我们还要训练,训练的话就涉及到一个反传,在普通的模型并行当中,我们的反传和前传时间轴是如下图所示:
我们先前传完,再依次反传。但是在我们流水线并行里面,其实反传也是一个流水线的过程。但是这里面有个特殊的地方,注意一下重新前传(或重算)。如果我们不重新前传的话,意味着我们前面的这些中间结果都要保留着等待反传结束后才能丢弃/释放,这意味着我的宝贵的显存又要被浪费了,这样子的话我们还不如算完就全部扔掉,因为我已经把结果交给下一块 GPU 了,暂时就不需要了。而反传时我们还需要中间结果的时候,我大不了再重算一次(换句话说每张卡只要保留自己的输入就可以了)。重算后我们可以正常做反传,得到关于输入的梯度,然后把这份梯度传给上一张卡。上一张卡同样执行重算、反传和发送梯度,直到所有卡都完成了梯度计算。
重新前传的操作叫做 checkpoint 或 sublinear,在 PyTorch 里面有 checkpoint,在 MegEngine 里也有 sublinear,我们目前实现的是非常粗粒度的 sublinear,它不是中间保留几个结果重算部分就可以了,它其实是全部都重算了,这就是GPipe。
前传还是一样的代码,如上图左侧给大家做一个参考。
反传是精妙的地方,我们拿到 label,loss 以后看一下,第一就是我们 GradManager,这是 MegEngine 一个非常重要的特性,就是 GradManager 可以对中间的 feature(就是中间结果)进行求导,所以我们可以在计算过程中对中间变量进行 attach,在 GPipe 的场景下,我们需要的是对输入的导数,所以我们在一开始就 attach 输入数据 x,然后进行前传(或者称为重算)。如果它是最后一张卡的话,我们就计算相应的损失,并把梯度算出来。通过 grad\_to\_prev\_gpu,我们把关于输入的梯度传给了上一张 GPU。后一块卡关于输入的梯度即前一块卡输出的梯度 dy。我们通过 gm.backward(dy=grad)手动指定梯度,从而完成中间 GPU 的求导过程。这就是一个简单的 GPipe。
如果大家想试着玩一下这个 GPipe 的话,在 GitHub 上面 MegEngine Parallel Tutorial(https://github.com/zhouyizhua... 是我写的,大家可以去跑一下玩一下。
专栏文章推荐
- 分享实录上篇:利用 MegEngine 分布式通信算子实现复杂的并行训练
- CVPR 2021 | 大幅涨点!新型动态激活函数ACON和轻量级网络TFNet
- Python 和 C/C++ 拓展程序的性能优化
欢迎关注旷视研究院极术社区专栏,定期更新最新旷视研究院成果
加入旷视:career@megvii.com