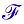引言
LFSR(线性反馈移位寄存器)用于产生可重复的伪随机序列PRBS,该电路由n级触发器和一些异或门组成。在每个时钟周期内,新的输入值会被反馈到LFSR内部各个触发器的输入端,输人值中的一部分来源于LFSR的输出端,另一部分由LFSR各输出端进行异或运算得到。
该电路具有以下特点:
- 如果初始状态相同,则最终会得到相同的输出序列(即输出序列是确定的);
- 输出序列趋向于随机序列(伪随机);
- 经过一定次数的迭代后,你将得到与初始状态相同的状态值;(最大重复间隔可由(2^n- 1)计算,其中n为移位寄存器的数目)
由于上述特性,LFSR主要用于生成PN序列(伪噪声序列)。
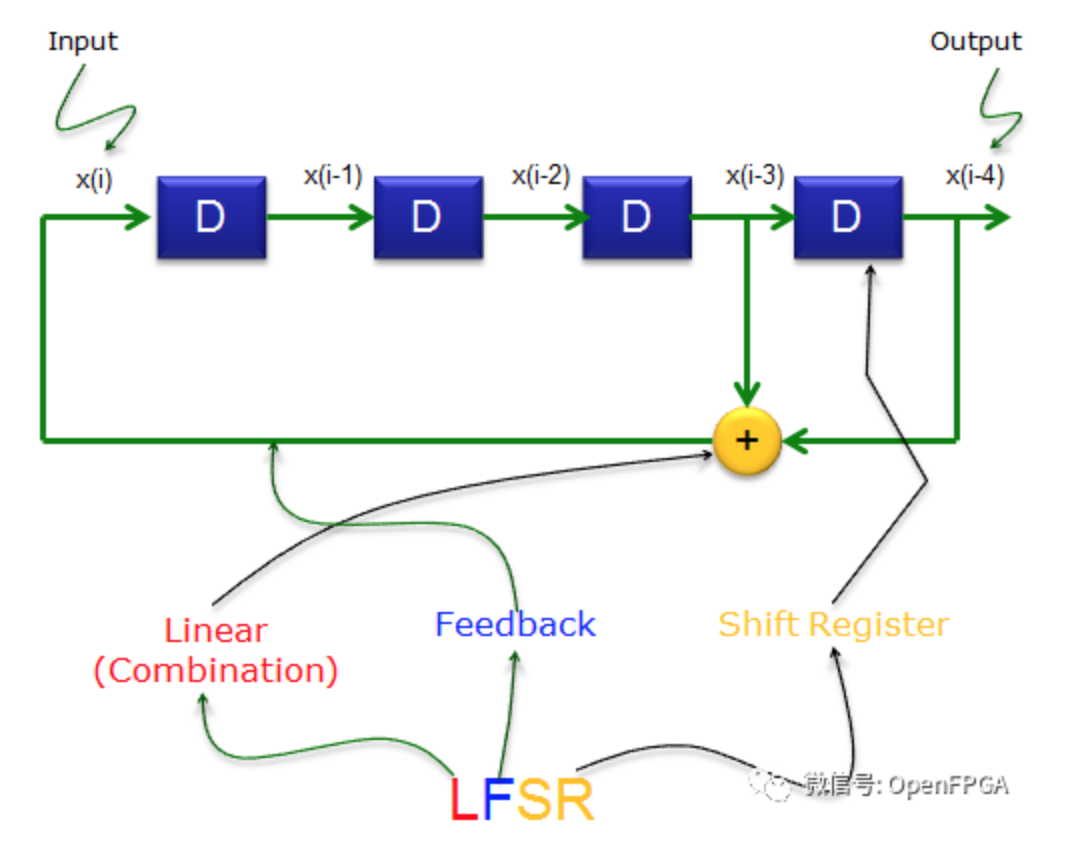
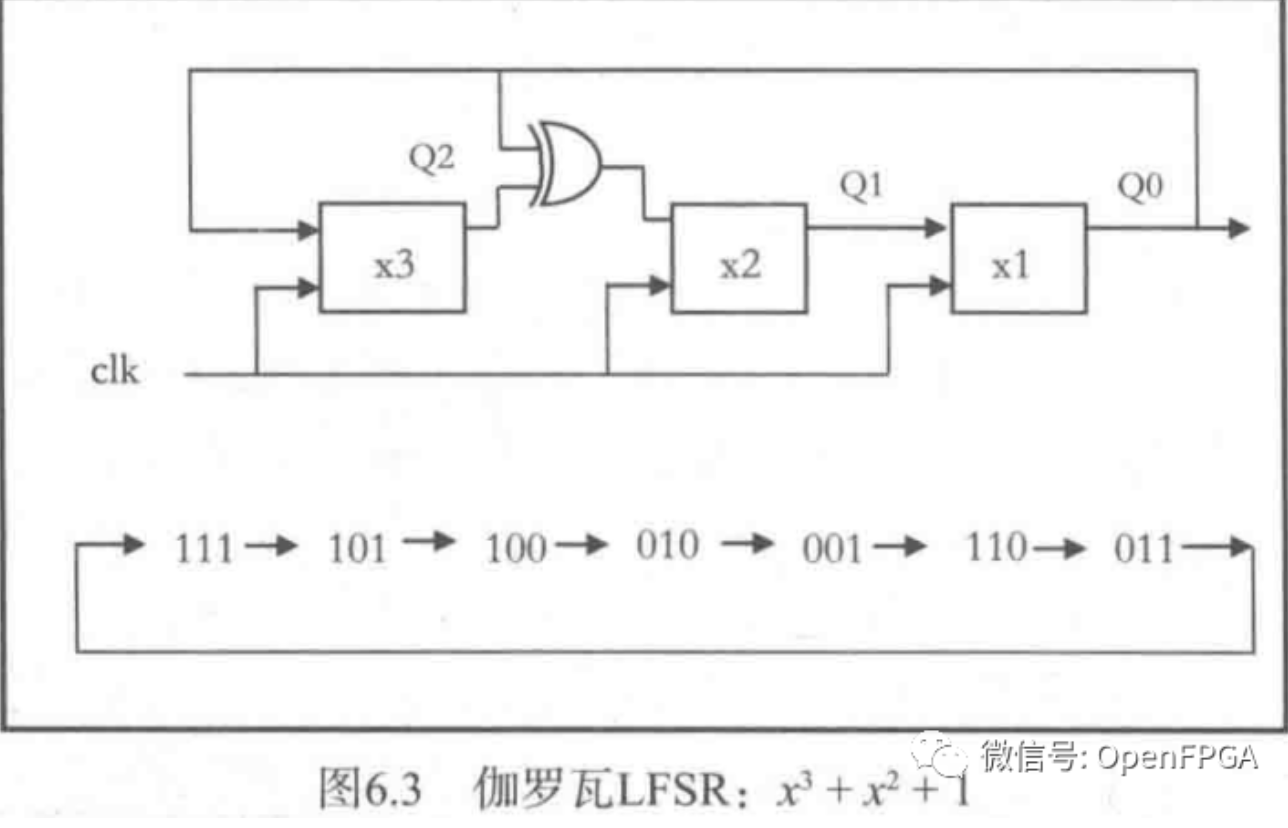
LFSR的初始值被称为伪随机序列的种子,其最后一个触发器输出的就是一个周期性重复的伪随机序列。由n个触发器构成的LFSR电路可以产生一个周期为2^n-1的序列。以3比特LFSR为例,触发器依次重复出现111,101,100,010,001,110及011这7种组合,最后一个触发器输出的就是一个周期为7的伪随机序列。目前有两类常用的LFSR电路:斐波那契LFSR与伽罗瓦LFSR下面分别进行介绍。
斐波那契LFSR与伽罗瓦LFSR
斐波那契LFSR也可称为多到一型LFSR,即多个触发器的输出通过异或逻辑来驱动一个触发器的输入。
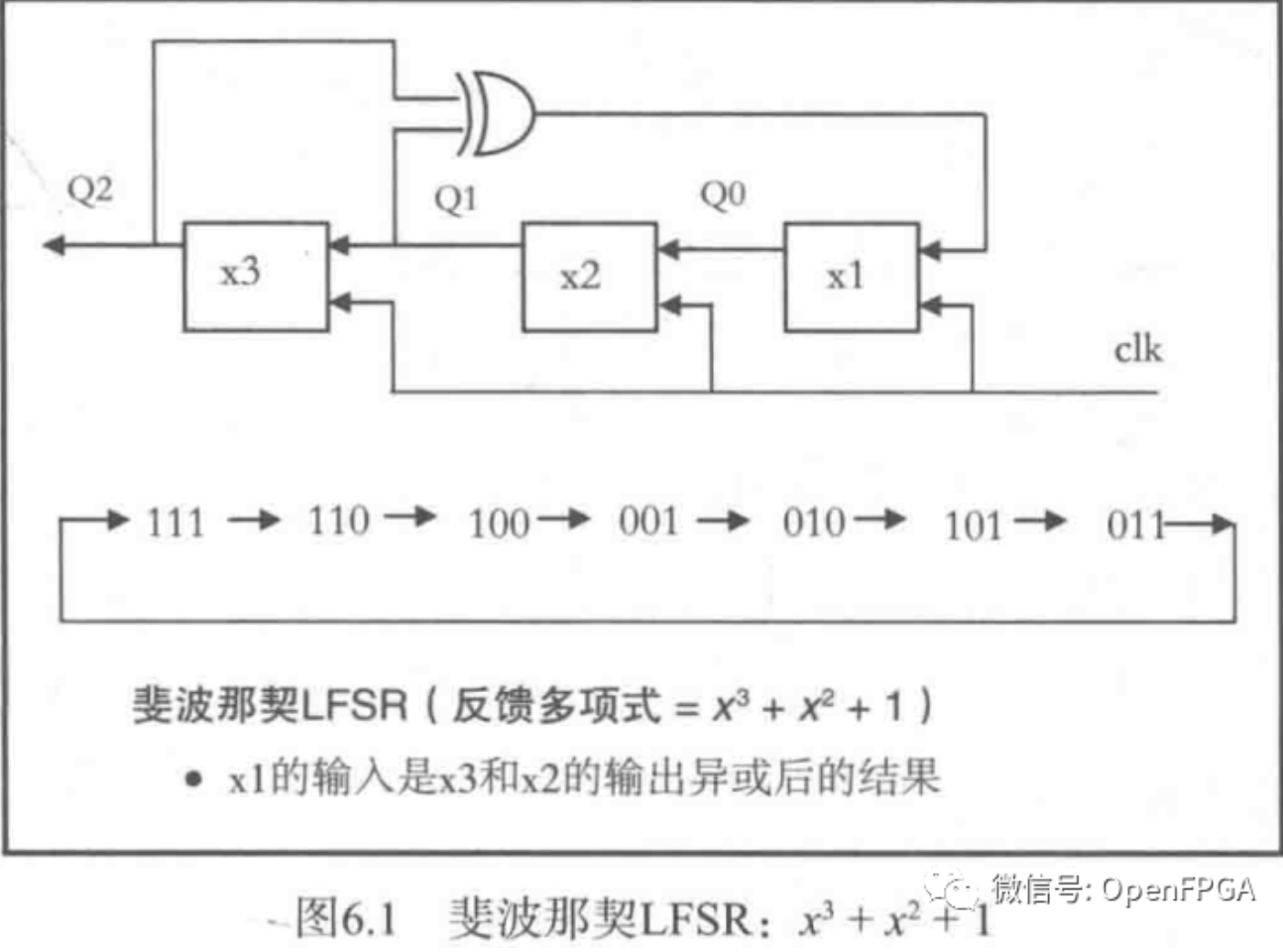
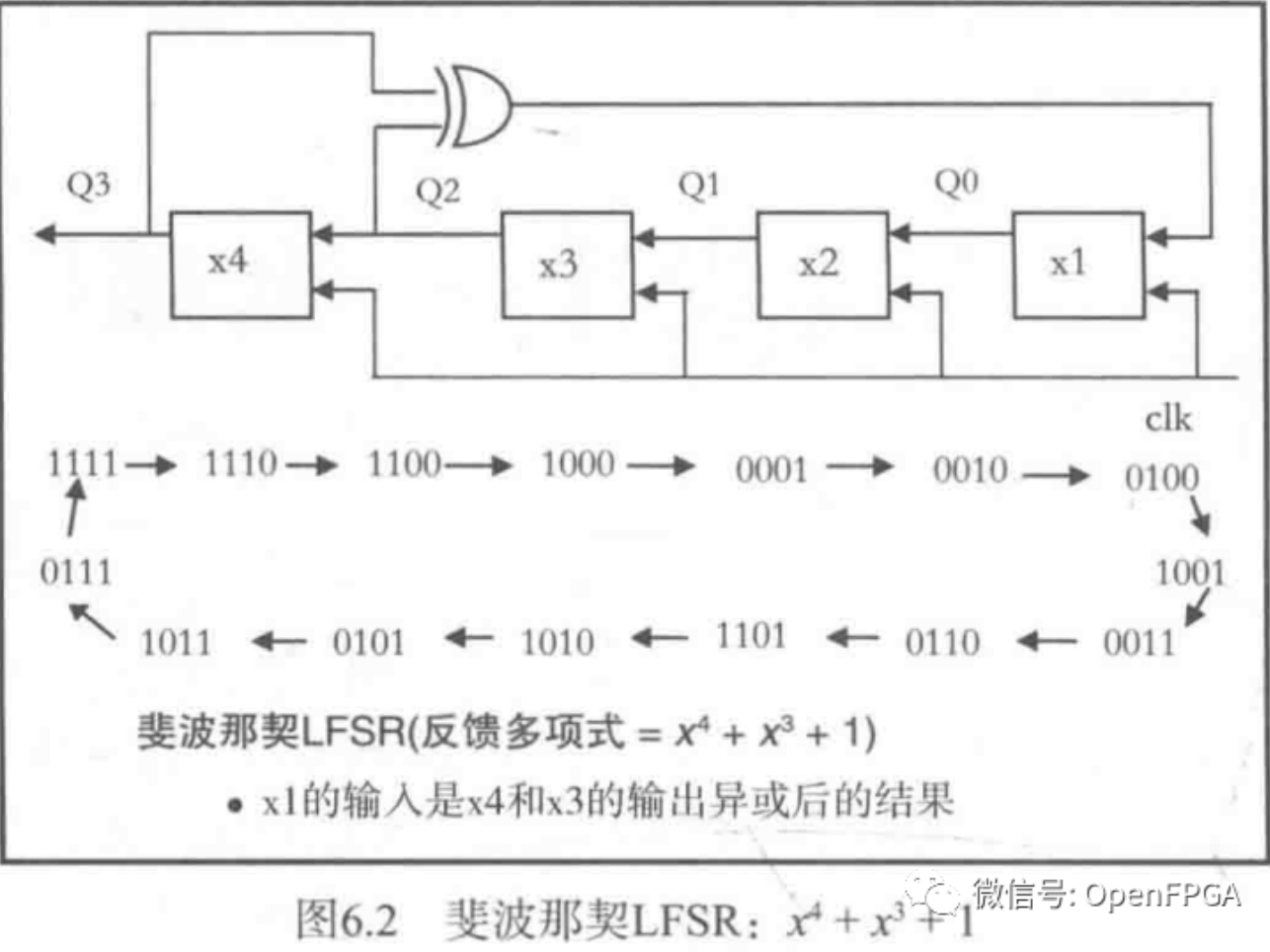
与此相反,伽罗瓦LFSR为一到多型LFSR,即一个触发器的输出通过异或逻辑驱动多个触发器的输入。这两种电路都产生(2^n-1)序列,但是一到多型LFSR具有更高的速度,因为它的两个触发器之间仅使用一个异或门。图6.1至图6.3是3比特和4比特LFSR的具体电路。
伽罗瓦LFSR(反馈多项式为x^3+x^2+1):
- 触发器xl的输入通常来自于触发器x2的输出;
- x3(最高项)的输入通常来自于xl的输出;
- 此多项式中剩余触发器的输入是xl的输出与其前级输出异或的结果;
- x2的输人由x1的输出与x3的输出通过异或运算得到。
LFSR电路可用于构建高速计数器,LFSR计数器与二进制计数器有何不同呢?二进制计数器产生重复且规整的输出序列,而LFSR计数器产生的序列是近似随机的。我们是否可以从LFSR链中任意位置取值并且通过异或逻辑产生伪随机序列呢?答案是肯定的,这样可以产生伪随机序列,但此时序列的长度可能不是最长的。换言之,对于由n个触发器构成的LFSR而言,选择合适的反馈多项式不仅可以产生伪随机序列,而且可以产生最大长度的伪随机序列。
LFSR反馈多项式
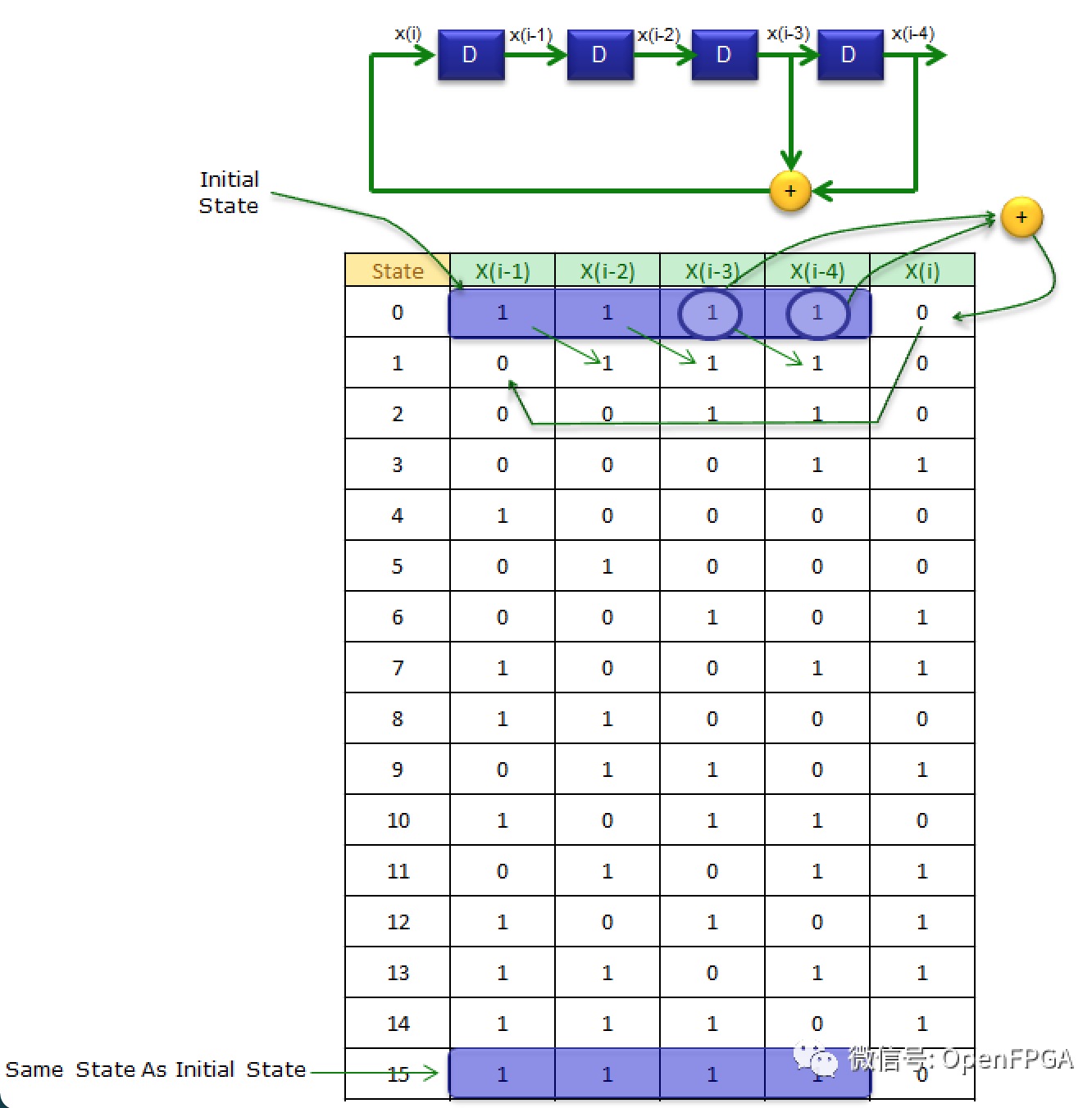
本电路中每次迭代的状态转换如下表所示,在这个表中,你会发现到上面列出的所有属性。
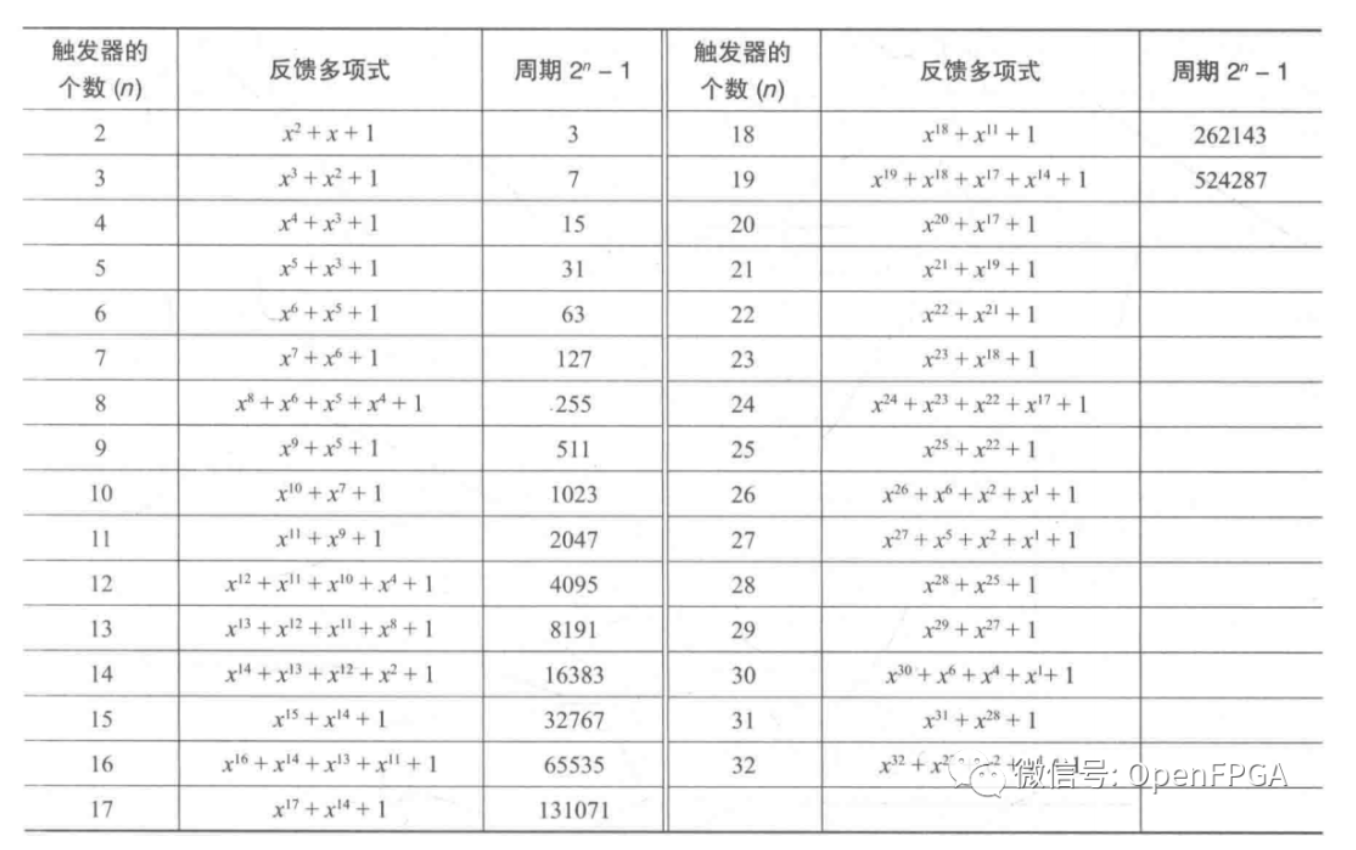
产生最大长度伪随机序列的反馈多项式如下表所示。表中给出了n取不同值时产生最大长度伪随机序列的反馈多项式。需要注意的是,对于任意给定的移位寄存器长度n,可能存在不止一个产生最大长度伪随机序列的反馈多项式。
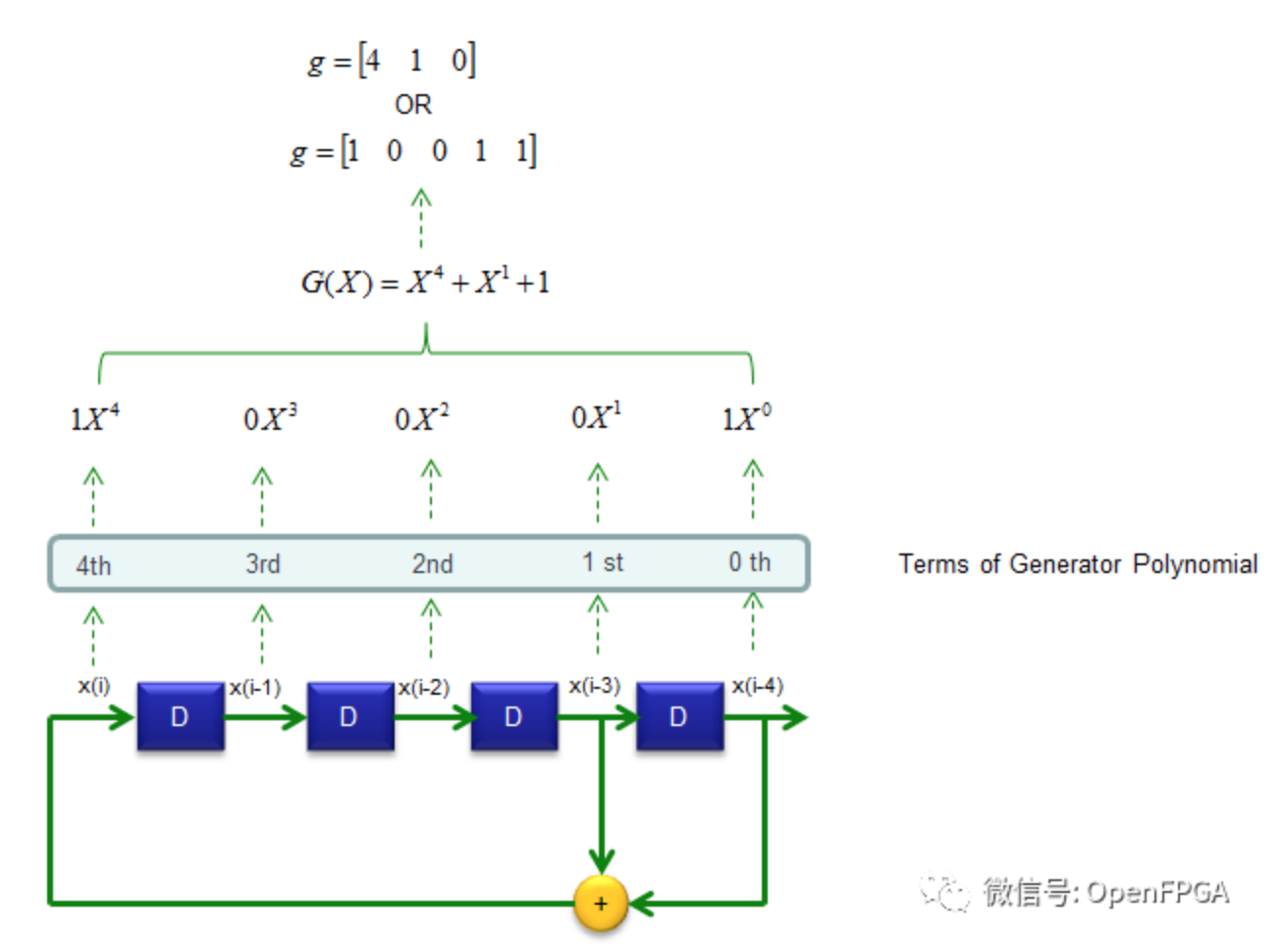
在上面表述中这个电路被表示为一个多项式,但是你会发现很难把真实的电路和生成的多项式联系起来,下面的插图将帮助你理解生成的多项式的含义。
//上图中,原作者可能存在一个错误,应该是1X^1, 而不是0X^1
//理解:反馈路径存在,取1;反之,取0。x^4 、x和x^0存在,x^3和x^2不存在,所以是【1 0 0 1 1】
LFSR的用法
LFSR具有广泛的应用, 下面对其中的一些典型应用进行介绍。
LFSR计数器
LFSR可用于构建通过随机序列状态进行计数的计数器。与常见的计数器相比, LFSR计数器具有速度快 、 消耗逻辑门少的特点。
扰码器/解扰器
LFSR可用作扰码器来产生重复的比特图案。当重复间隔较大时, 该比特图案看上去就像一个随机的比特序列。用户数据发送前和扰码器生成的序列进行异或, 然后发出, 此时发送的数据就是经过扰码的数据。接收电路与发送电路采用相同的多项式, 这样, 解扰器就可以将发送端原始的用户数据恢复出来。
LFSR还可应用于其他领域, 如密码系统 、 BIST ( 内建自测试)、 快速以太网及吉比特以太网等。
扩展:m序列
m Sequence (MLS : Maximum Length Sequence)
m序列是一类特殊的LFSR序列,为了更好的理解m序列,首先你需要理解LFSR序列的概念。
与典型的LFSR相比,m序列有什么特别之处?
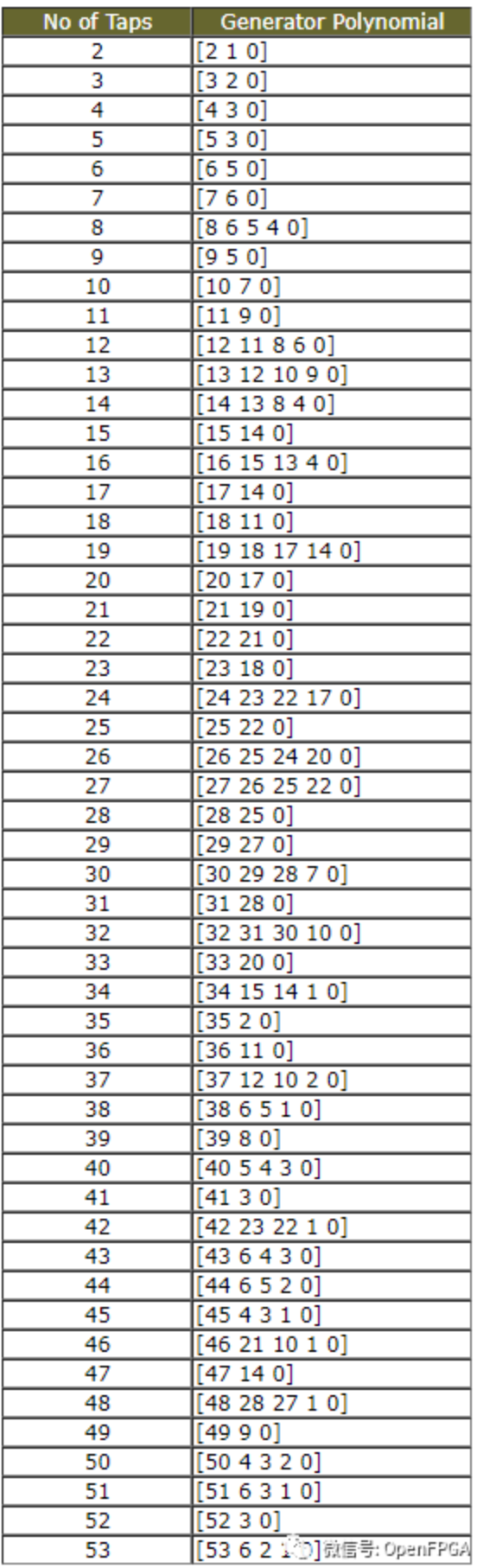
如果使用LFSR生成一个序列,输出最终会重复它自己,但是在大多数应用程序中,其目的是使用给定数目的移位寄存器(后续用taps表示这些寄存器)生成尽可能长的非重复序列。m-Squence 是一种特殊类型的LFSR,它为每个给定的taps提供了最长的非重复序列。
下表显示了各种taps的已知m序列:
参考链接:http://mail.sharetechnote.com...\_Communication\_LFSR.html
原出处:FPGA 的逻辑
作者:碎碎思
相关文章推荐
更多FPGA技术干货请关注FPGA 的逻辑技术专栏。