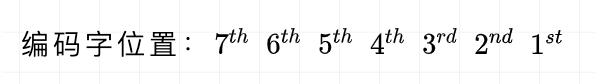在过去的50到60年中,检错与纠错技术有了长足的发展。现今我们对检错和纠错理论有了更好的理解,并且该理论还在不断的发展。编码理论已经成为一个特殊的技术领域,主要研究检错与纠错技术及其背后的数学理论。这里我们将从应用角度讨论不同的检错与纠错技术,不过多地涉及数学细节。
在通信中,错误检测是第一步,错误纠正是第二步。在进行点对点数据传输或数据存储时可能发生错误。由于信道噪声的影响,当数据通过无线或有线通信媒介传输时,数据中会出现比特错误。接收到数据时,接收设备应检查数据是否在传输过程中发生了错误(如何检错将在后面进行探讨)。另外,当数据存储在CD硬盘、DRAM存储器或闪存中时,部分比特会由于不同原因而发生跳变,当我们读出这些数据时,应检测数据是否存在错误。
数据错误可能不会造成什么影响,也可能会导致严重的后果。如果我们听CD上的音乐,当出现比特错误时,会影响音乐质量。然而,如果列车的信号数据出错,后果将会是致命的。考虑到严谨性与重要性,我们会采用不同的检错及纠正方法。
检错
数据以0、1比特序列的方式进行传输,为了能够发现错误比特,我们需要额外添加一些数据与原始数据一起传输,这些额外比特通常称为冗余比特。就净荷而言,这些比特是冗余的,因为它们不是真正的用户数据,然而它们对于检错与纠错来说却是至关重要的。这些冗余比特不是完全随机的,它们与数据比特之间具有数学相关性。如果一些比特出错(1变 为0,0变为1),我们可以通过这些冗余比特及其与数据比特的数学相关性判断出是否发生了错误。如果冗余比特数量达到一定程度,我们就不仅可以发现错误,还可以纠正这些错误。
奇偶校验是我们通常使用的一种检错方式,它是通过添加1个奇偶校验位来实现的。例如,我们可以为每7个数据比特添加1个奇偶校验比特,构成一个8比特组。如果采用偶校验方式,那么每个8比特组中1的个数为偶数,对于奇校验方式,每个8比特组中1的个数为奇数。在接收端,接收电路针对每个8比特组计算1的个数,如果1的数量不符合规则,则可以 确定其中出现了错误。这种编码方式可以发现奇数个比特错误,不能发现偶数个比特错误。奇偶校验可以发现奇数个比特错误,但不能找出发生错误的具体位置,因此不能实现纠错功能。
CRC校验是数据包传输中常用的检错机制。在PCIe以太网或者SATA中的数据帧被传输之前,CRC校验模块针对数据帧中的原始数据计算一个校验结果并与数据帧一同传输。接收电路重新计算CRC值,并且将其与接收到的CRC值进行比较。如果二者不匹配,就认为数据包中出现了错误,否则认为数据帧正确。在这些协议中,CRC校验用于发现错误。对于大多 数应用来说,发现错误即可,不必对错误进行纠正。当接收电路发现CRC错误时,可以通过上层协议进行数据帧的重传。
错误纠正
对于一些应用,仅仅发现错误是不够的。它们需要既可以发现错误,又可以纠正错误。对于存储设备来说,在没有纠错手段的情况下,如果一些比特位发生了错误,那么就不会有其他的方法(如重传)来纠正这些错误,无论读多少遍都不会实现纠错。在一些通信系统中,纠错也是十分重要的。在过去的半个多世纪中,大量的研究工作都集中于纠错编码技 术。在此,让我们先对通信系统有个基本的理解,并且清楚哪些方面是需要纠错技术的。
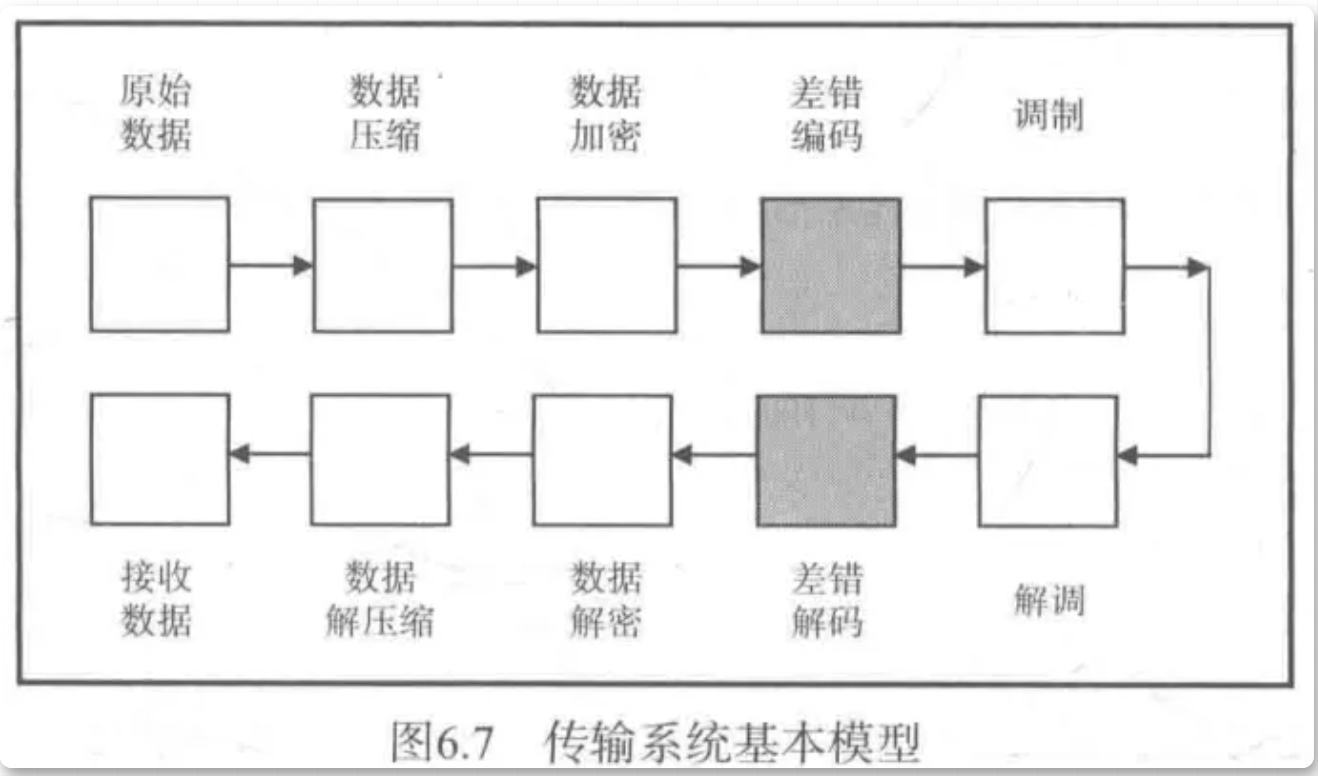
图6.7中的数据压缩部分用于对原始的用户数据进行压缩,减少需要传输或存储的数据量。数据加密单元可以对用户信息进行加密,避免非法用户截获数据后恢复出原始的用户信息。差错编码单元通过增加冗余数据对加密后的数据进行检错或纠错编码。调制器将基带数据调制为适合信道传输的线路信号,在有线或无线介质中传输,传输过程中会由于噪声等原因W引入错误。
接收端以相反的方式处理接收到的信号。解凋器负责将模拟信号转换成数据比特流。差错解码单元会检查数据中是否出现了错误,如果是纠错编码,那么还可以进行纠错。需要说明的是,差错解码单元的纠错和检错能力与其具体编码方式和错误本身的特点(如单个错误还是连续突发错误)都有直接关系。解密和解压缩单元对接收的数据进行解密和解压缩处理,并最终得到接收数据。下面我们将重点讨论检错和纠错技术。
纠错编码
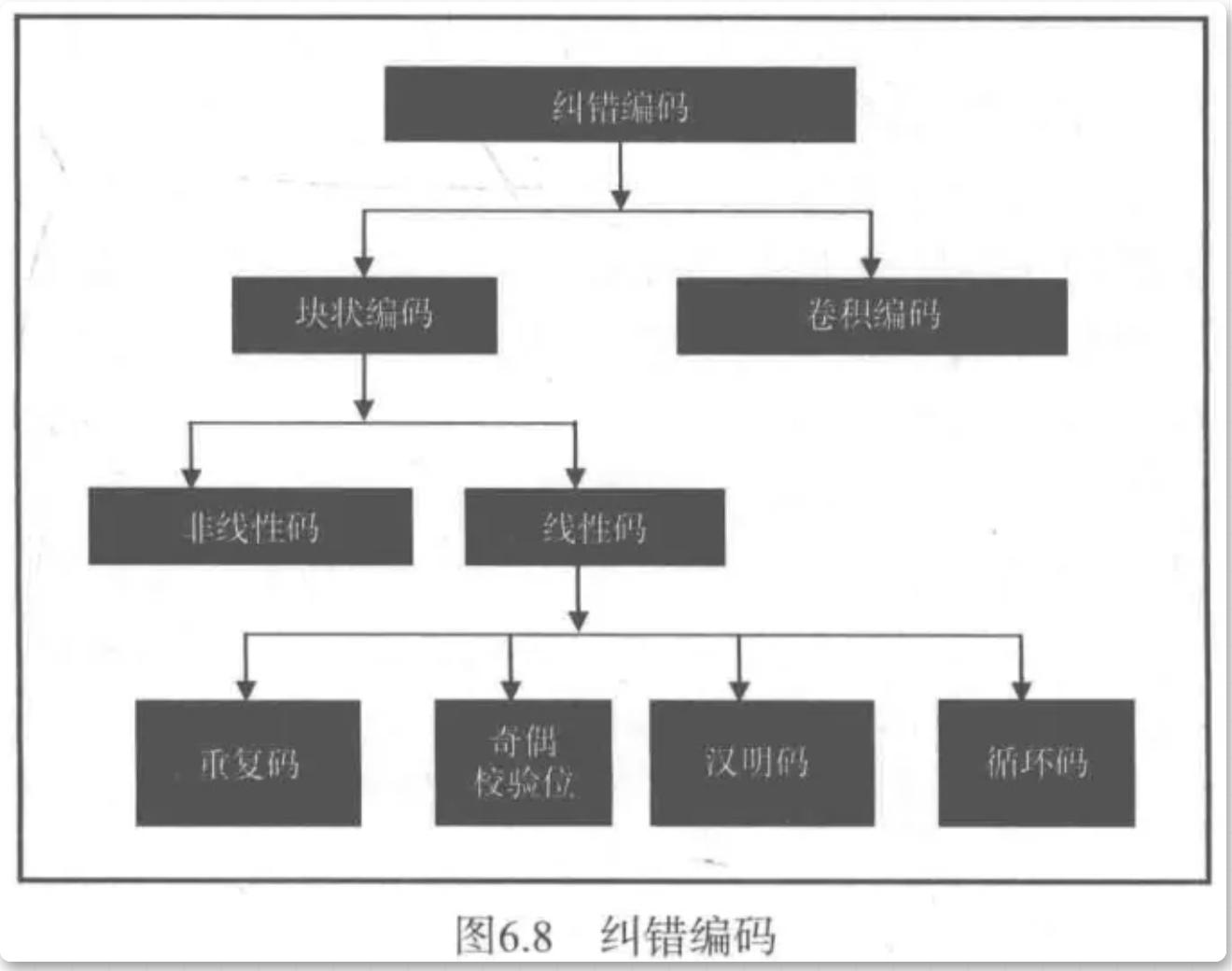
纠错编码分为两种,如图6.8所示,一种是块状编码(简称为块状码或分组码),一种是卷积编码(简称为卷积码)。
块状码
进行块状编码时, 需要将用户数据埘分成固定长度的组, 针对每一组计算并添加冗余比特。我们以Flash ( 闪存 ) 为例, 其内部的数据被划分为512比特( 每一块数据的比特数n = 512 ) 的块, 针对每个块有k个按照一定算法生成的冗余比特。这些冗余比特是根据n比特数据产生的奇偶校验比特。数据比特(n) 及冗余比特(k)共同构成编码字, 这 n+k 比特被存储在闪存中。从闪存中读出数据时,n+k比特被读出, 此后需要根据编码规则进行错误纠正。在块状码中, 两个编码块之间不存在相互关联, 每个数据块独立地进行错误纠正,与其他数据块无关。
卷积码
与块状码不同, 卷积编码的当前编码输出不仅与当前输入有关, 还与此前的输入有关。
线性编码
它是块状码的一种, 两个编码字的线性组合可以构成另外的编码字,汉明码是线性码的一种,下面将对此进行讨论。
汉明码
汉明码是一种线性码,对于一个长度为比特的编码块,有n个冗余比特,其余的为数据比特。常用的汉明码有(7,5)和15,11)。(7,5)汉明码表示编码块长度为7,其中包括4个数据比特和3个冗余比特。每个冗余比特都是部分数据比特按照一定方式进行异或运算(等效于选择部分比特进行奇偶校验运算)得到的。汉明码是一个线性编码集合,每个编码块都可以检测岀两个以内的比特错误,可以纠正单比特错误。
汉明间距(d):两个编码块中对应位不同的比特数量。下面是一些例子:
- 000与111的d为3,即这两串比特间不同比特的个数为3。
- 0000与1111的d为4,即这两串比特间不同比特的个数为4。
- 最小汉明间距(d\_min))是所有编码字中汉明距离最小的那个汉明间距。
对于最小汉明距离为d的编码,可以检测岀1个比特错误,可以纠正(d\_min-l)/2个比特的错误。例如,000变为110,101,011,可以判断岀编码中有错误发生。如果000变为010或001,那么可以判断出哪个比特发生了错误。
例如,我们的目标是发送4个数据比特,要求接收电路可以纠正任何单比特错误。对于4个比特,共有16种有效的比特组合方式,0000,0001,…,1111。接下来,根据编码规则,需要为每个比特组合增加3个冗余校验位构成长度为7的编码字。对于普通的7比特编码,共有128种组合方式,但对于汉明码来说,仍然只有16种有效的编码,这些编码之间的最小汉明距离为3,此时接收端可以纠正任何单比特错误。
为了形成长度为7比特的汉明码编码字,先放置校验比特,它们占据位置(2^0,2^1和2^2),即为第一个、第二个和第四个比特位置。数据比特依次占据其他比特位置构成完整的代码字。
编码字位置:
数据/校验比特:d3 d2 d1 p2 d0 p1 p0
在上表中, d表示数据比特, p表示校验比特。校验比特应满足下面的式子。
校验比特p0的计算公式:
p0+d0+d1+d3=0(应该得到偶校验结果)
校验比特p1的计算公式:
p1+d0+d2+d3=0
校验比特p2的计算公式:
p2+d1+d2+d3=0
根据所给出的三个公式,可以计算岀汉明码的全部编码字。下表为汉明距离为3的7比特编码字列表,编码字中加粗显示的是数据比特,剩下的是校验比特。通过观察,我们可以发现所有编码字的最小汉明距离都为3。
可以看出,为了纠正错误,编码字中需要有相对较多数量的校验比特和相对较少的数据比特。对于(7,4)汉明码,其有效净荷占4/7=57%;对于(15,11)汉明码,其有效净荷占11/15=73%。
在纠正单比特错误时,校验比特数量p和数据长度之间的关系为:p=log(2)D+1。
我们以闪存中使用的512比特的数据块的校验为例,令d=512,则p=log(2)512+1=10。编码字中的数据长度越大,则编码效率越高(512/522=98%)。然而,这会造成成错误纠正能力的降低。此时可以在512比特中纠正单比特错误。错误纠正能力越强,有效负荷所占的比例就会越低。在实际应用中,在冗余度可接受的情况下,错误纠正能力越强越好。
自1950年汉明码被一个美国数学家理查德•汉明发明后,还有很多种块状码方式被发明出来。需要注意的是,在实际应用中,编码技术和解码技术是同时需要的,并且解码技术通常更为复杂一些。下一部分将讨论汉明码在DDR存储器中的应用。
汉明码应用举例—DDR ECC
DDR存储器中使用了(72,64)汉明码作为纠错码,DDR存储器由多个宽度为8比特的存储芯片(DIMM)构成。DDR存储器的数据位宽通常为64比特(由8个DIMM并行实现)。为了发现并纠正单比特错误,我们需要7个冗余的ECC(Error Correction Code,纠错编码)比特。ECC比特被存储在独立的DIMM中。ECC比特产生于编码阶段,与数据一同被写入存储器中。当从存储器中读取数据时,ECC比特一同被读出,并被译码器用来发现两个比特的错误,纠正一个比特的错误。
编码
对于一组数据比特,发送电路产生校验比特(CB)并将其与数据比特一同发送。
- 每个时钟周期DDR控制器将64位比特数据写人外部存储器(DIMM)中;
- 对于64位比特数据,我们需要生成7位校验比特;
- 通常这些CB被写入一个独立的DIMM中(因为DIMM可以存储8比特,因此产生8个CB而不是7个);
- 这些CB称为CB0、CB1、CB2、CB3、CB4、CB5、CB6及CB7;
- 存储CB的DIMM中的冗余比特不是用户数据,它们可以被用来发现2比特的错误和纠正单比特的错误;
- 每个周期,存储控制器持续产生CB并与对应的数据比特同时写人DIMM中。
解码
- 当存储控制器从DIMM中读取数据时,也同时读取存储在独立DIMM中的8比特CB。
- 用于读取数据的地址同样被用来读取CB这样读出的CB和所读出的数据就是一一对应的;
BCH编码
- BCH编码是循环码的一种,由Hocquenghem在1959年发明;
- BCH编码可以纠正编码块中的多个比特错误;
- 二进制BCH编码的首次译码由Peterson在1960年实现,其所使用的译码算法目前已经被其他算法优化和改进(Berlekamp,Massey,Chien,Forney等),分别被称为Berlekamp-Massey算法、Chien查找算法、Forney算法等。
- BCH编码广泛地用于存储设备,如硬盘、固态盘、CD及DVD中。
BCH编码用BCH ( n,k,t ) 表示,n为编码字长度, k 为数据比特个数, t是可被纠正的错误比特数。
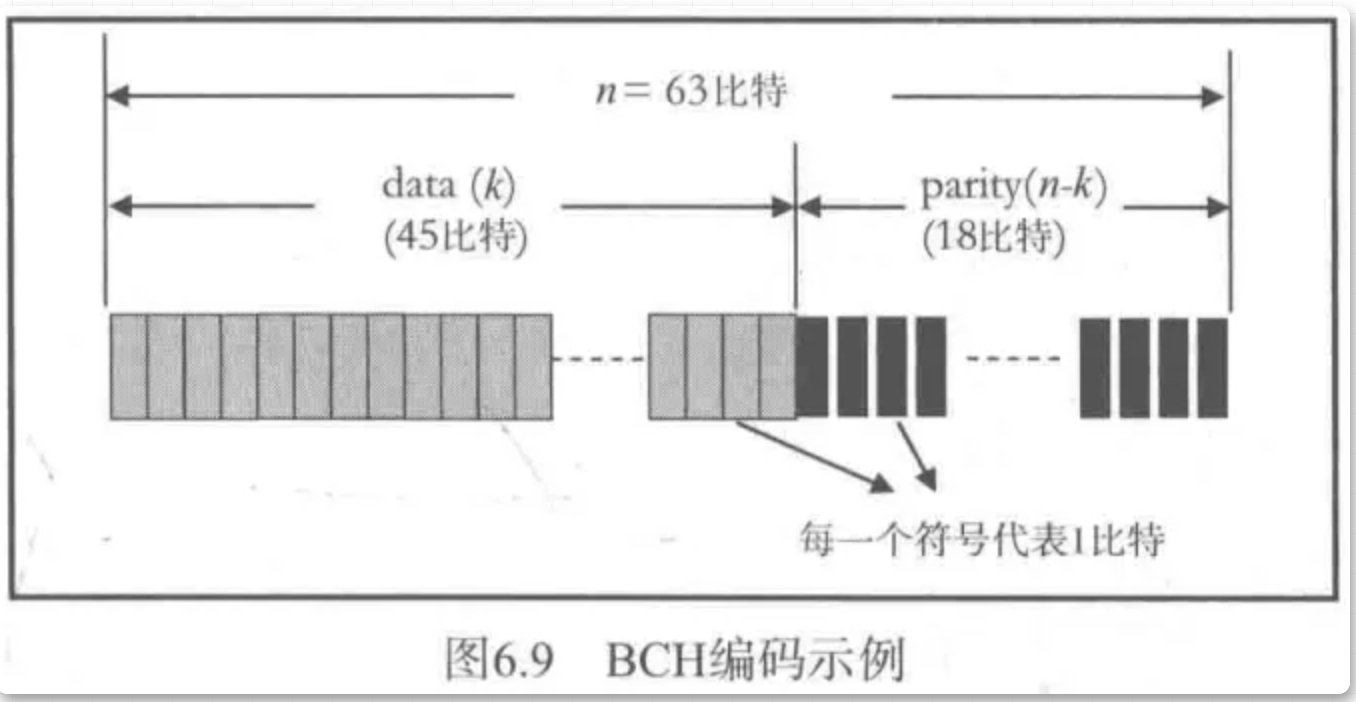
例子:BCH ( 63, 45, 3 )
这意味着对于45个数据比特的码块, 如果我们希望能够纠正任何3个及以内的比特错误, 此时需要18个校验位, 最终编码字的长度为63比特。如果我们需要牺牲纠错能力, 提高数据比特所占的比例, 可以选择BCH ( 63, 51, 2 )。此时, 编码字段长度为63时, 数据长度为51比特, 可以纠正2比特的错误。也就是说, 根据特定的需要( 纠错能力 、 编码字段中数据所占的比例 、 编码块长度 ), 我们可以设计出所需要的编码。BCH ( 63, 45, 3 ) 编码示例如图6.9所示。
里德-所罗门编码
- 里德-所罗门编码(R-S编码)由伊万斯-里德及古斯塔夫-所罗门在1960年发明,如图6.10所示;
- R-S编码可以发现多个符号(symbol)错误,这与BCH编码能够发现多个比特错误是不同的;
- R-S编码不是二进制循环码,它所面对的不是比特,而是由多个比特构成的符号;
- 由于它能够纠正多个错误符号(每个符号可以涵盖多个连续的比特),因此适用于纠正突发错误;
- R-S编码被用到CD,DVD,及WiMAX等领域;
- R-S编码被表示为RS(n,k),n为编码字总个数(包括数据符号及校验符号),k为数据符号个数,这意味着有n-k个校验符号;
- 以一个比较流行的R-S编码RS(255,223)为例:
■ 译码器能纠正编码字中任何位置上出现的16个符号错误,通常为校验符号数的一半;
■ 其中包括32个校验符号,译码器可以纠正任意16个符号错误(可以是数据符号、校验符号或各占一部分);
■ 当一个符号中有一个比特、全部比特或任意比特发生错误时,我们说一个符号发生了错误。
软判决与硬判决.
通信系统中,数字比特流调制成模拟信号后进行传输。在接收端,通过对模拟输入采样来决定在每个周期它是1还是0。采用硬判决时,接收的模拟电平与固定的阈值进行比较,判断接收的是1或0。例如,将阈值设定为0.5V,那么大于0.5V时判决为逻辑1,低于0.5V时判决为逻辑0。如果对接收的电平采样后得到的电平值与0.5V偏差较远,那么这种判决方式是可行的,例如,采样电平为0.8V,那么可以将其判断为1,如果采样电平为0.2V,可以将其判断为0,此时这种硬判决方式得到的判决结果是可信的。
但如果采样电平在阈值附近(如0.55V),我们就很难确定其是1还是0了,此时再采用上述判决方式就有可能带来较大的误码率。上述这种判决方式被称为硬判决,此时对电平的判决仅仅依靠其自身的电平,没有利用接收的比特流之间的相关性(编码方式带来的接收数据之间的相关性)对其进行综合判断。
软判决就是除电平信息之外,还要结合接收信号所采用的编码方式,对接收的采样信号进行综合判断,得出最有可能的判决结果,这种方式被称为软判决。目前软判决得到了广泛的应用,通常可以采用DSP实现,以提高系统的纠错能力。
原出处:IC设计
作者:碎碎思
相关文章推荐
更多FPGA技术干货请关注IC设计技术专栏。