概念介绍
在介绍算法之前,我们回顾下基本概念:
- |X|:X的度数,(无向图中)节点的邻居个数。
- CFG:控制流图。
- successor:本文指CFG中基本块的后继。
- 四元式:(op,result,arg1,arg2),比如常见的
a=b+c就可以看作四元式(+,a,b,c)。 - SSA(Static Single Assignment):静态单赋值。
- use/def:举个例子,对于指令
n: c <- c+b来说 use[n]={c,b},def[n]={c}。 - live-in:当以下任一条件满足时,则称变量a在节点n中是live-in的,写作a∈in[n]。节点n本文中代表指令。
- a∈use[n];
- 存在从节点n到其他节点的路径使用了a且不包括a的def。
- live-out: 变量a在节点n的任一后继的live-in集合中。写作a∈out[n]
- 干涉:在某一时刻,两个变量在同一
live-in集合中。 - RIG(Register Interfere Graph): 无向图,其点集和边集构成如下:
- 节点:变量
- 边:如果两节点存在干涉,那么这两节点之间就有一条干涉边
- k-着色:给定无向图G=(V,E),其中V为顶点集合,E为边集合。将V分为k个组,每组中没有相邻顶点,可称该图G是k着色的。当然可着色前提下,k越小越好。
需要注意的是,我们后续的算法会作用在最普通的四元式上,而不是SSA。在介绍寄存器分配算法之前,我们需要活跃变量分析来构建干涉图。
活跃变量分析与图着色算法
活跃变量分析
简单来说,就是计算每个点上有哪些变量被使用。
算法描述如下[1]:
`input: CFG = (N, E, Entry, Exit)
begin
// init
for each basic block B in CFG
in[B] = ∅
// iterate
do{
for each basic block B other than Exit{
out[B] = ∪(in[s]),for all successors s of B
in[B] = use[B]∪(out[B]-def[B])
}
}until all in[] do't change`活跃变量分析还有孪生兄弟叫Reaching Definitions,不过实现功能类似,不再赘述。
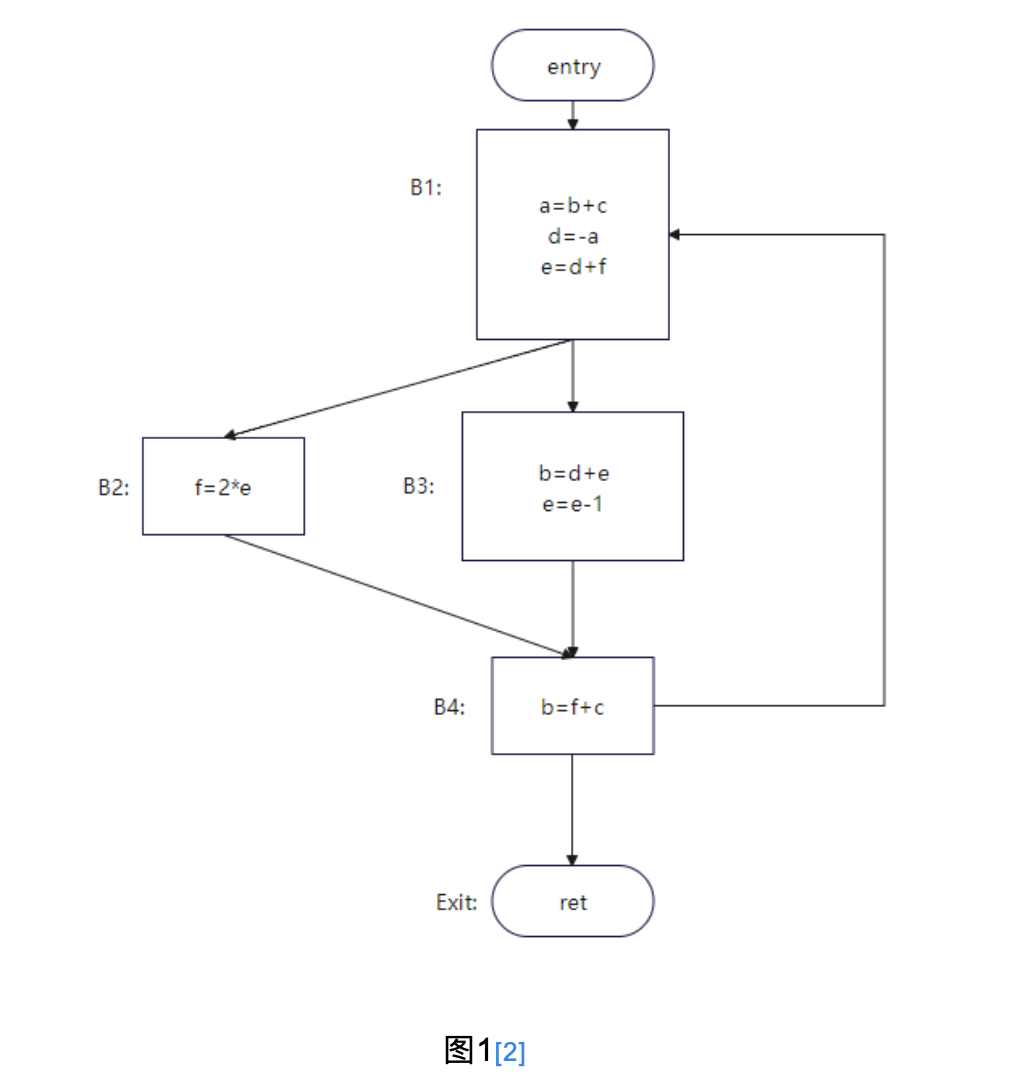
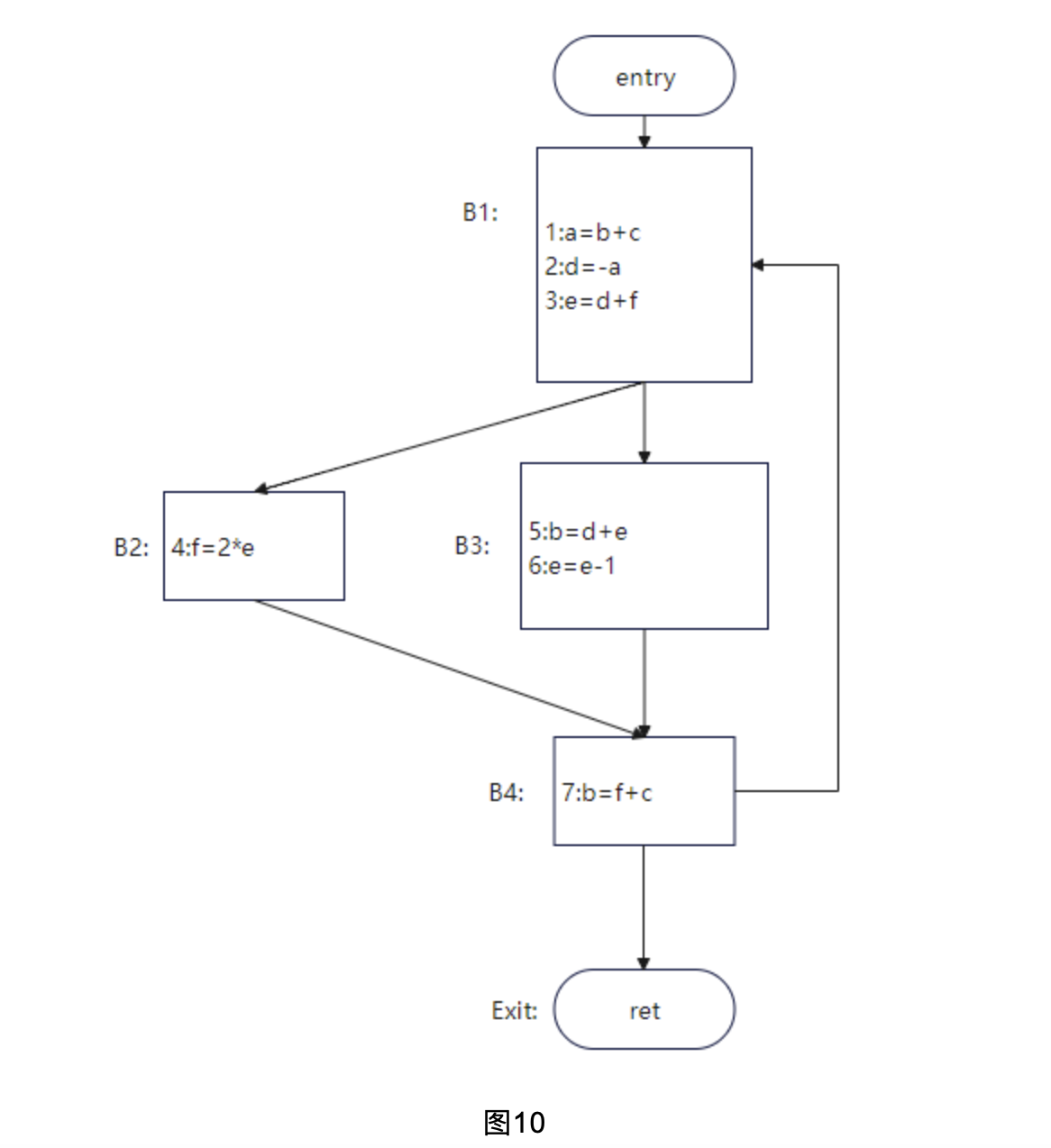
举个例子:对图1的代码进行活跃变量分析
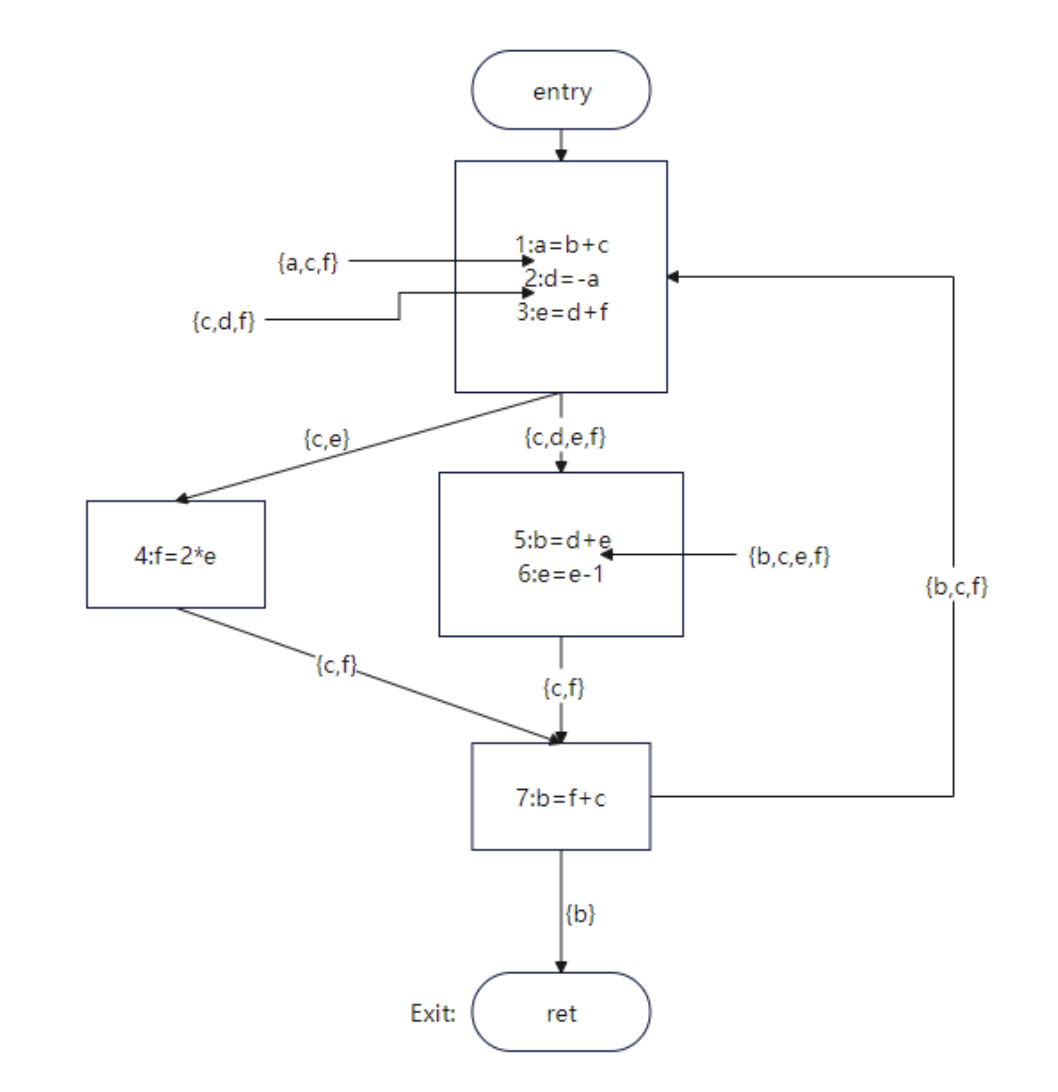
可以得到每个点的活跃变量如图2所示:
过程呢?限于篇幅,仅仅计算第一轮指令1的结果,剩余部分读者可自行计算。
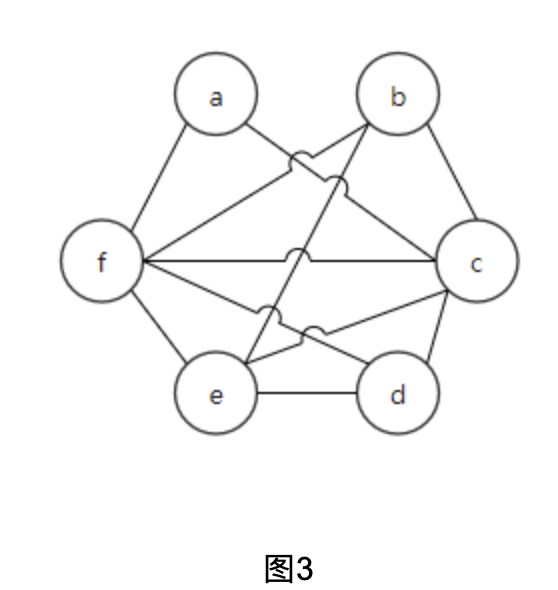
可画出RIG如图3:
图着色
经过上文的活跃变量分析,我们得到了干涉图,下一步对其进行上色。
但是图着色是一个NP问题,我们会采用启发式算法对干涉图进行着色。基本思路是:
- 找到度小于k的节点;
- 从图中删除;
- 判断是否为可着色的图;
- 迭代运行前3步直到着色完成。
算法描述[3]:
`input: RIG, k
// init
stack = {}
// iterate
while RIG != {} {
t := pick a node with fewer than k neighbors from RIG // 这里RIG可以先按度数排序节点再返回
stack.push(t)
RIG.remove(t)
}
// coloring
while stack != {} {
t := stack.pop()
t.color = a color different from t's assigned colored neighbors
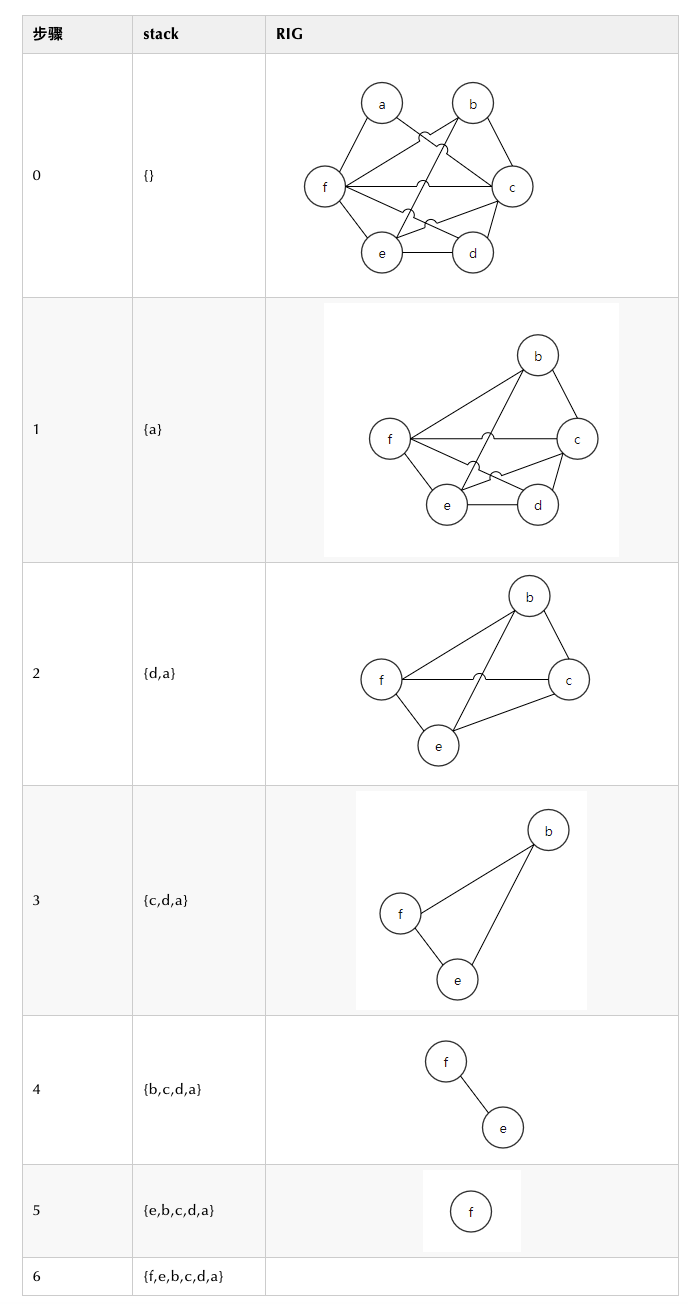
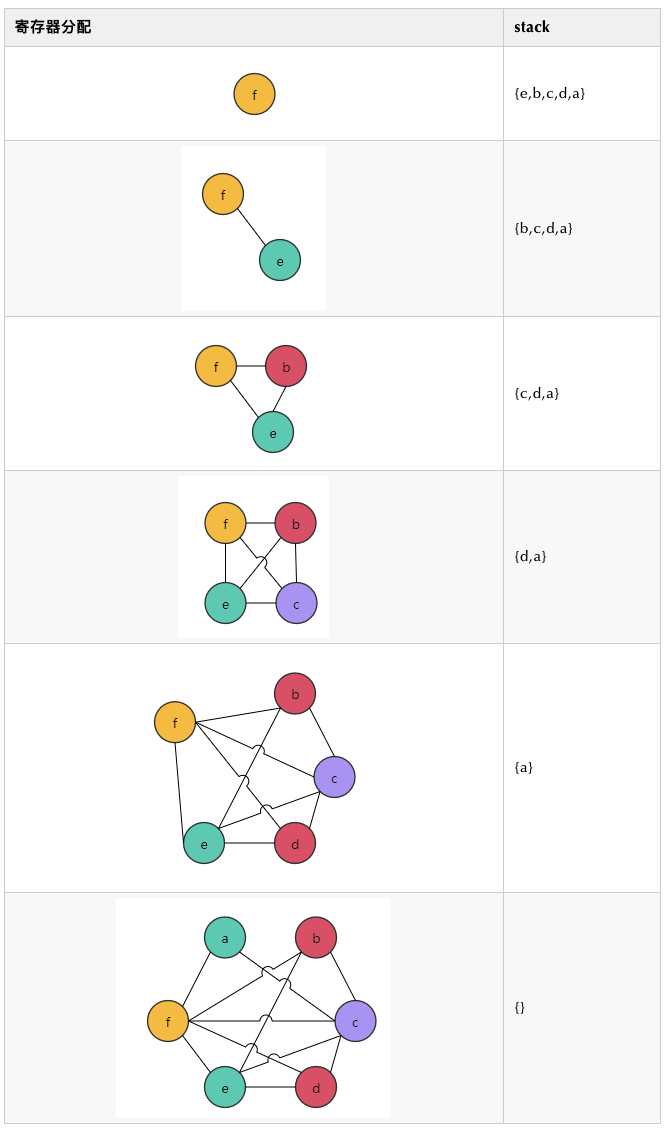
}`对于例子1,假设有4个寄存器r1、r2、r3、r4可供分配。
寄存器分配
所以图3中的RIG是4-着色的。但如果只有三种颜色可用,怎么办呢?
没关系,我们还有大容量的内存,虽然速度慢了那么一点点。着色失败就把变量放在内存里,用的时候再取出来。
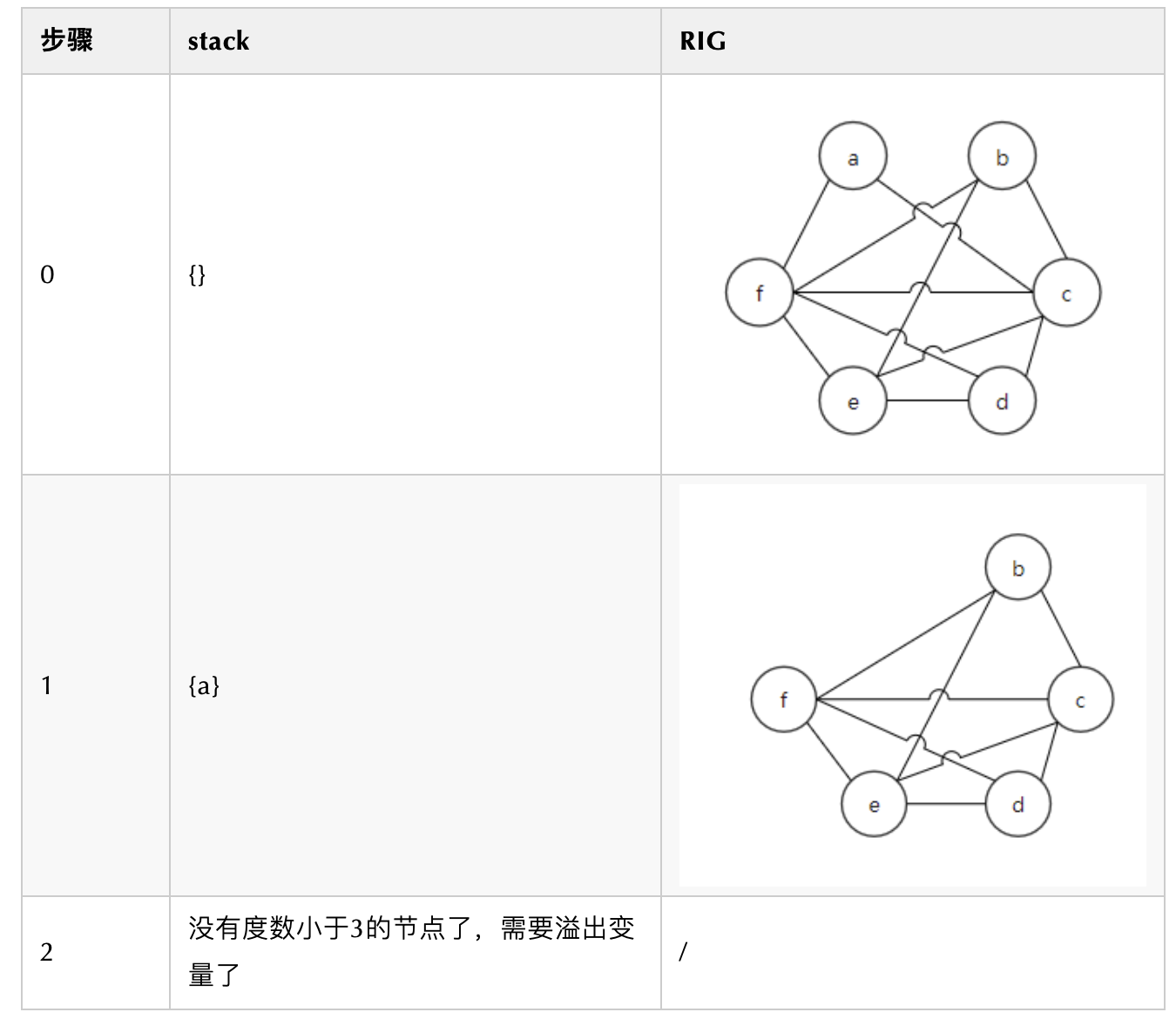
依然是上例,但是k=3,只有三个颜色。
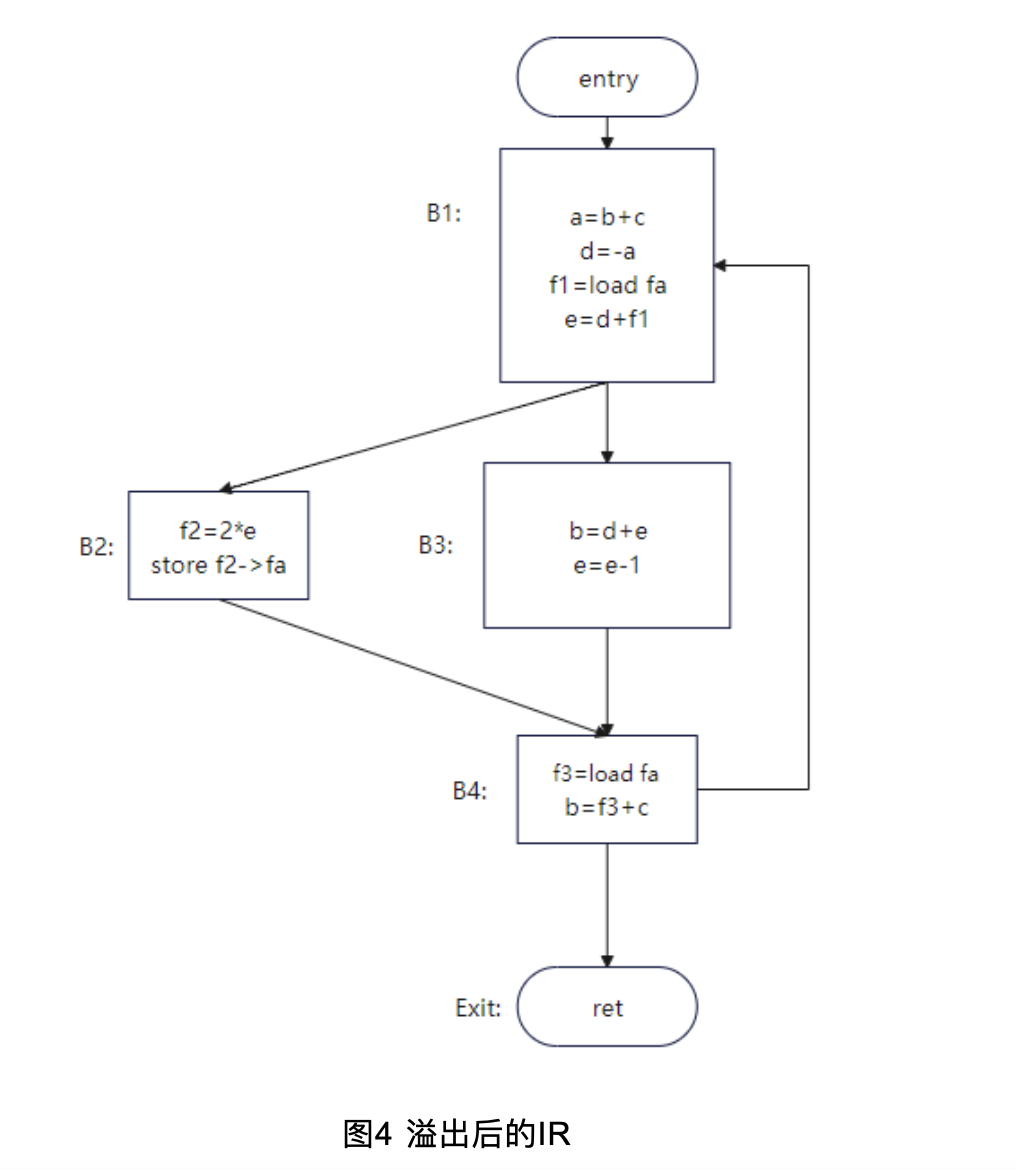
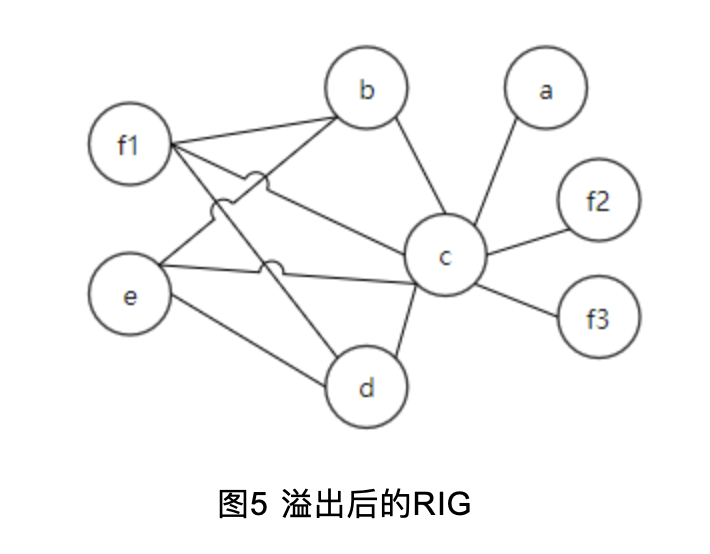
如果f的邻居是2-着色的就好了,但不是。那就只能选一个变量存入内存了。这里我们选择将变量f溢出至内存。溢出后的IR和RIG如图:
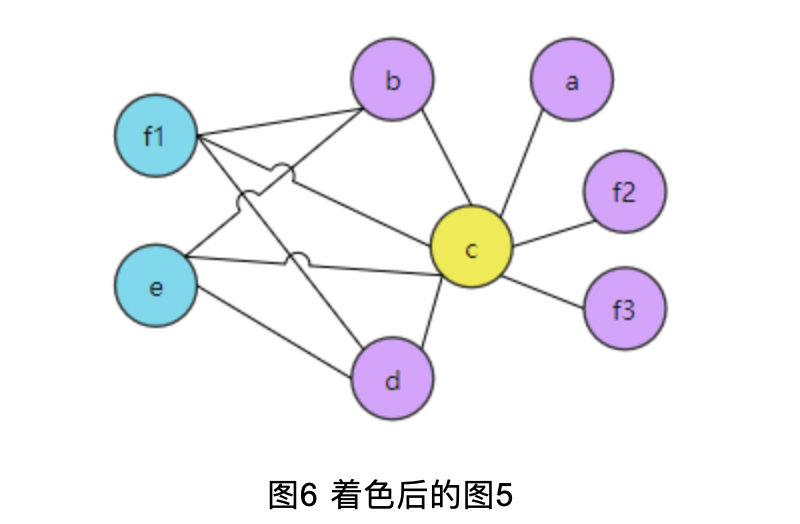
所以,溢出其实是分割了变量的生命周期以降低被溢出节点的邻居数量。溢出后的着色图如图6:
这里溢出变量f并不是明智的选择,关于如何优化溢出变量读者可自行查阅资料。
至此,图着色算法基本介绍完毕。不过,如果代码中的复制指令,应该怎么处理呢?
寄存器分配之前会有Copy Propagation和Dead Code Elimination优化掉部分复制指令,但是两者并不是全能的。
比如:代码段1中,我们可以合并Y和X。但是代码段2中Copy Propagation就无能为力了,因为分支会导致不同的Y值。
`// 代码段1
X = ...
A = 10
Y = X
Z = Y + A
return Z
// 代码段2
X= A + B
Y = C
if (...) {Y = X}
Z = Y + 4`所以,寄存器分配算法也需要对复制指令进行处理。如何处理?给复制指令的源和目标分配同一寄存器。
那么如何在RIG中表示呢?如果把复制指令的源和目标看作RIG中相同的节点,自然会分配同一寄存器。
- 相同节点?可以扩展RIG:新增虚线边,代表合并候选人。
- 成为合并候选人的条件是:如果X和Y的生命周期不重合,那么对于
Y=X指令中的X和Y是可合并的。 - 为了保证合并合法且不造成溢出:合并后局部的度数<k
那么如何计算局部的度数?介绍三种算法:
- 简单算法
- Brigg's 算法
- George's 算法
简单算法:
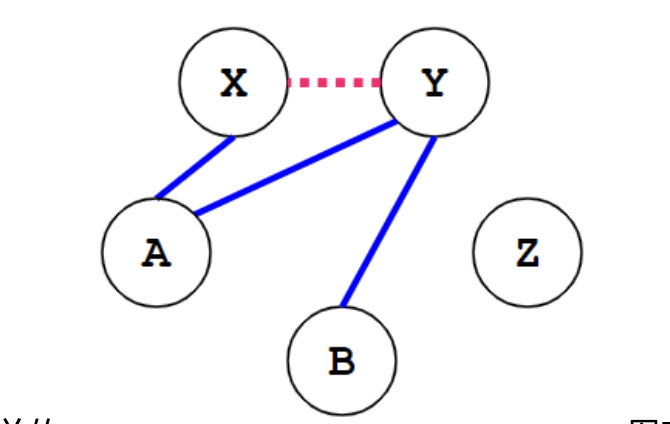
(|X|+|Y|)<k,很保守的算法但是可能会错过一些场景比如k=2时,图7应用简单算法是没办法合并的
图7\[3\]
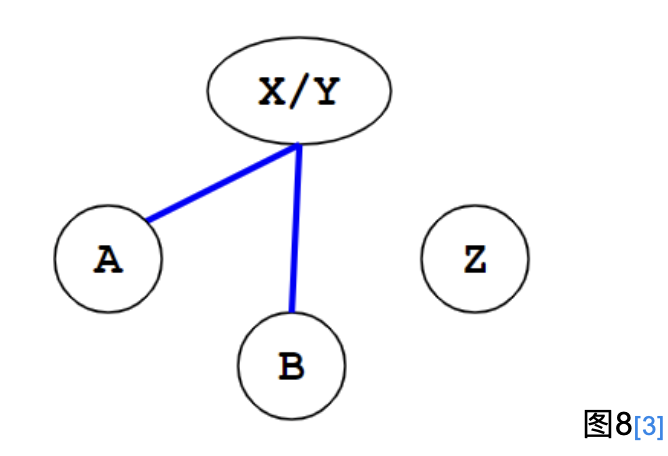
但明显图7可以合并成图8:
图8\[3\]
- Brigg's 算法:X和Y可合并,如果X和Y中度数≥k的邻居个数<k。但是如果X的度数很大,算法效率就不高
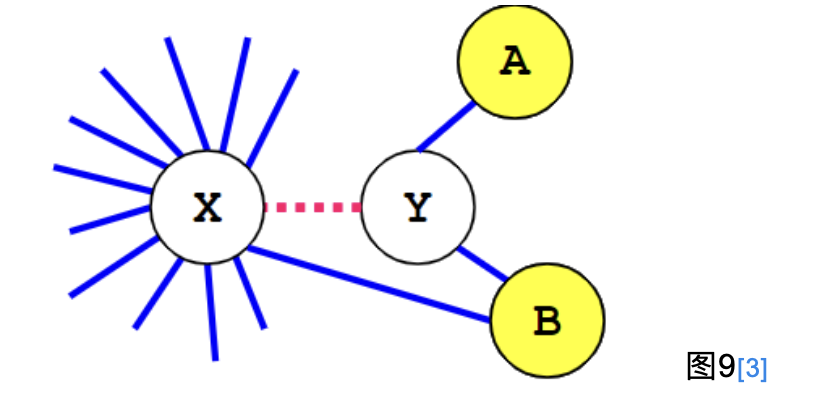
George's算法:X和Y可合并,如果对Y的每个邻居T,|T|<k或者T和X冲突。
比如k=2时,图9就可以合并X和Y。
相对于Brigg算法、George算法不用遍历节点的邻居。注意,图着色时可以按节点度数从小到大依次访问。
到此,图着色算法介绍完毕。
线性扫描
接下来介绍一种不同思路的算法:线性扫描。算法描述如下[4]:
`LinearScanRegisterAllocation:
active := {}
for i in live interval in order of increasing start point
ExpireOldIntervals(i)
if length(avtive) == R
SpillAtInterval(i)
else
register[i] := a regsiter removed from pool of free registers
add i to active, sorted by increasing end point
ExpireOldInterval(i)
for interval j in active, in order of increaing end point
if endpoint[j] >= startpoint[i]
return
remove j from active
add register[j] to pool of free registers
SpillAtInterval(i)
spill := last interval in active
if endpoint[spill] > endpoint[i]
register[i] := register[spill]
location[spill] := new stack location
remove spill from active
add i to active, sorted by increasing end point
else
location[i] := new stack location`
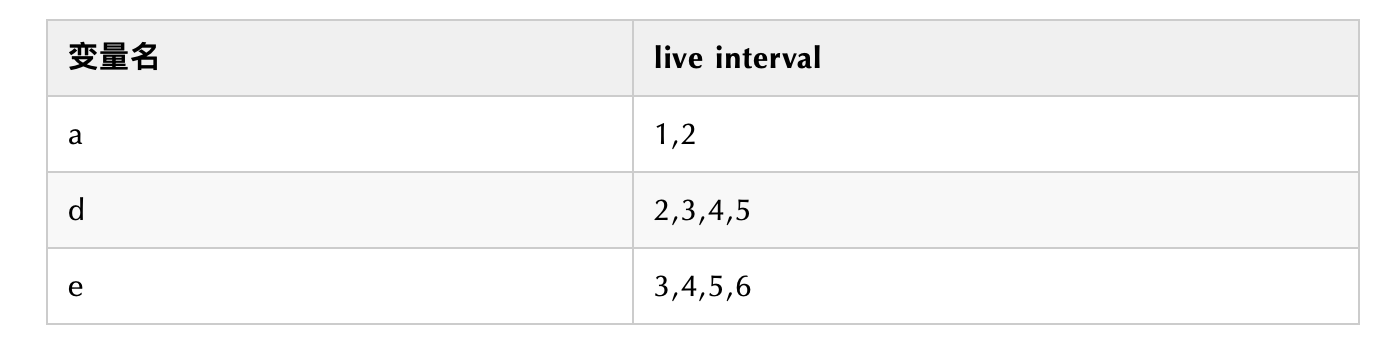
live interval其实就是变量的生命期,用活跃变量分析可以算出来。不过需要标识第一次出现和最后一次出现的时间点。
举个例子:
llvm中实现
在上文中介绍的算法都是作用在最普通的四元式上,但LLVM-IR是SSA形式,有PHI节点,但PHI节点没有机器指令表示,所以在寄存器分配前需要把PHI节点干掉,消除PHI节点的算法限于篇幅不展开,如感兴趣的话请后台留言。
llvm作为工业级编译器,有多种分配算法,可以通过llc的命令行选项-regalloc=pbqp|greedy|basic|fast来手动控制分配算法。
不同优化等级默认使用算法也不同:O2和O3默认使用greedy,其他默认使用fast。
fast算法的策略很简单,扫描代码并为出现的变量分配寄存器,寄存器不够用就溢出到内存。用途主要是调试。
basic算法以linearscan为基础并对life interval设置了溢出权重而且用优先队列来存储life interval。
greedy算法也使用优先队列,但特点是先为生命期长的变量分配寄存器,而短生命期的变量可以放在间隙中,详情可以参考[5]。
pbqp算法全称是Partitioned Boolean Quadratic Programming,限于篇幅,感兴趣的读者请查阅[6]。
至于具体实现,自顶向下依次是:
TargetPassConfig::addMachinePasses含有寄存器分配和其他优化addOptimizedRegAlloc中是与寄存器分配密切相关的pass,比如上文提到的消除PHI节点addRegAssignAndRewriteOptimized是实际的寄存器分配算法- 寄存器分配相关文件在lib/CodeGen下的RegAllocBase.cpp、RegAllocGreedy.cpp、RegAllocFast.cpp、RegAllocBasic.cpp和RegAllocPBQP.cpp等。
- RegAllocBase类定义了一系列接口,重点是selectOrSplit和enqueue/dequeue方法,数据结构的重点是priority queue。selectOrSplit方法可以类比上文中提到的SpillAtInterval。priority queue类比active list。简要代码如下:
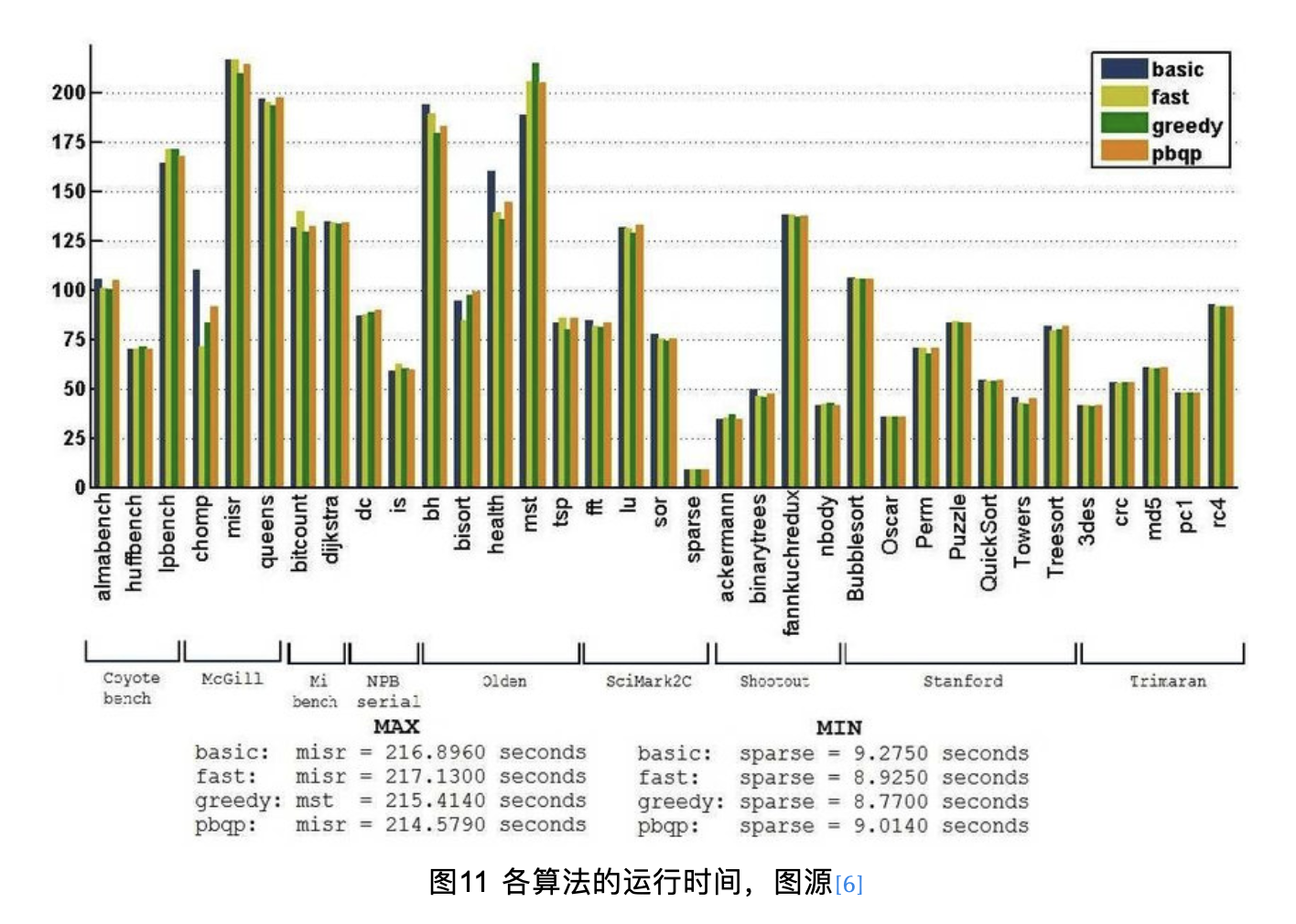
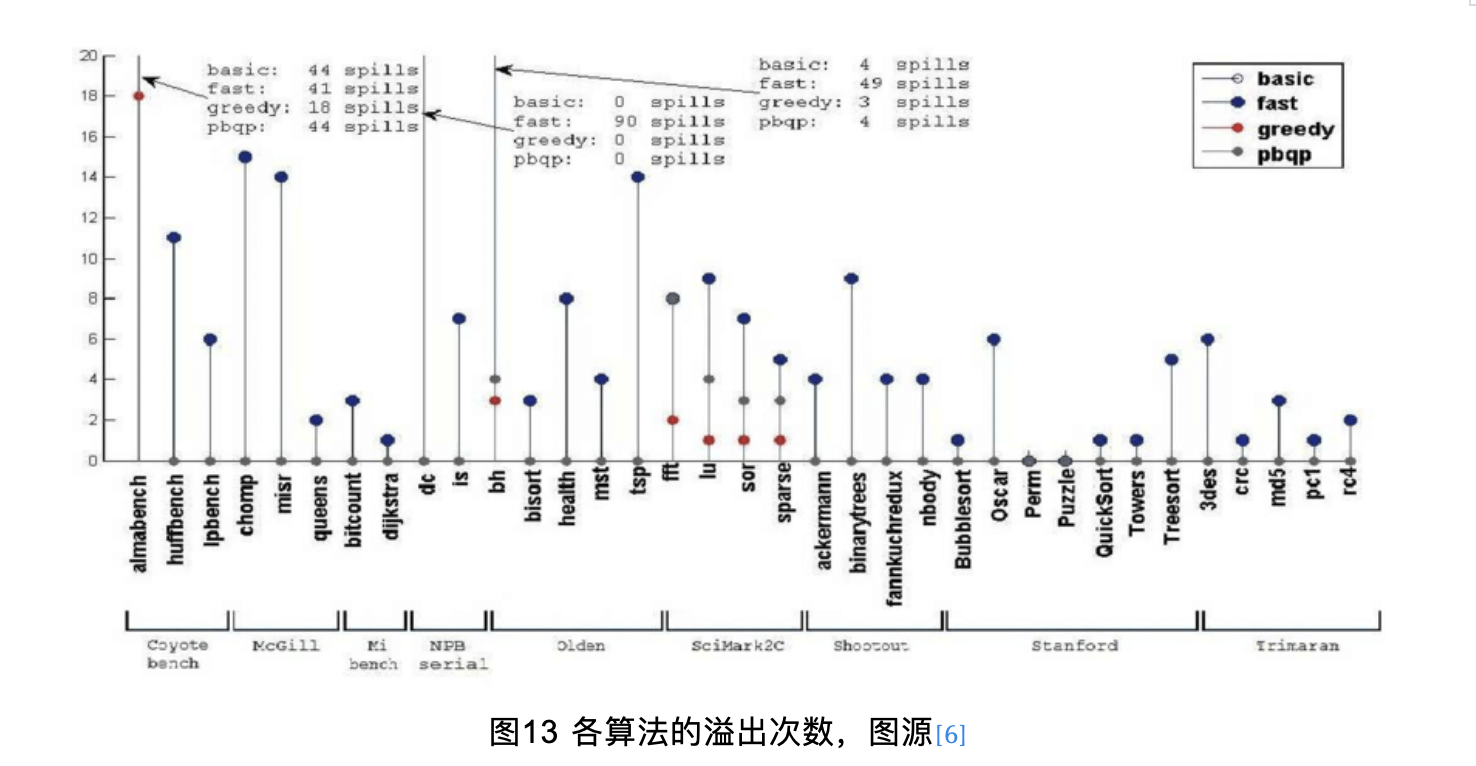
void RegAllocBase::allocatePhysRegs() { // 1. virtual reg其实就是变量 while (LiveInterval *VirtReg = dequeue()) { // 2.selectOrSplit 会返回一个可用的物理寄存器然后返回新的live intervals列表 using VirtRegVec = SmallVector<Register, 4>; VirtRegVec SplitVRegs; MCRegister AvailablePhysReg = selectOrSplit(*VirtReg, SplitVRegs); // 3.分配失败检查 if (AvailablePhysReg == ~0u) { ... } // 4.正式分配 if (AvailablePhysReg) Matrix->assign(*VirtReg, AvailablePhysReg); for (Register Reg : SplitVRegs) { // 5.入队分割后的liver interval LiveInterval *SplitVirtReg = &LIS->getInterval(Reg); enqueue(SplitVirtReg); } }}至于这四种算法的性能对比,我们主要考虑三个指标:运行时间、编译时间和溢出次数。
横坐标是测试集,纵坐标是以秒为单位的运行时间
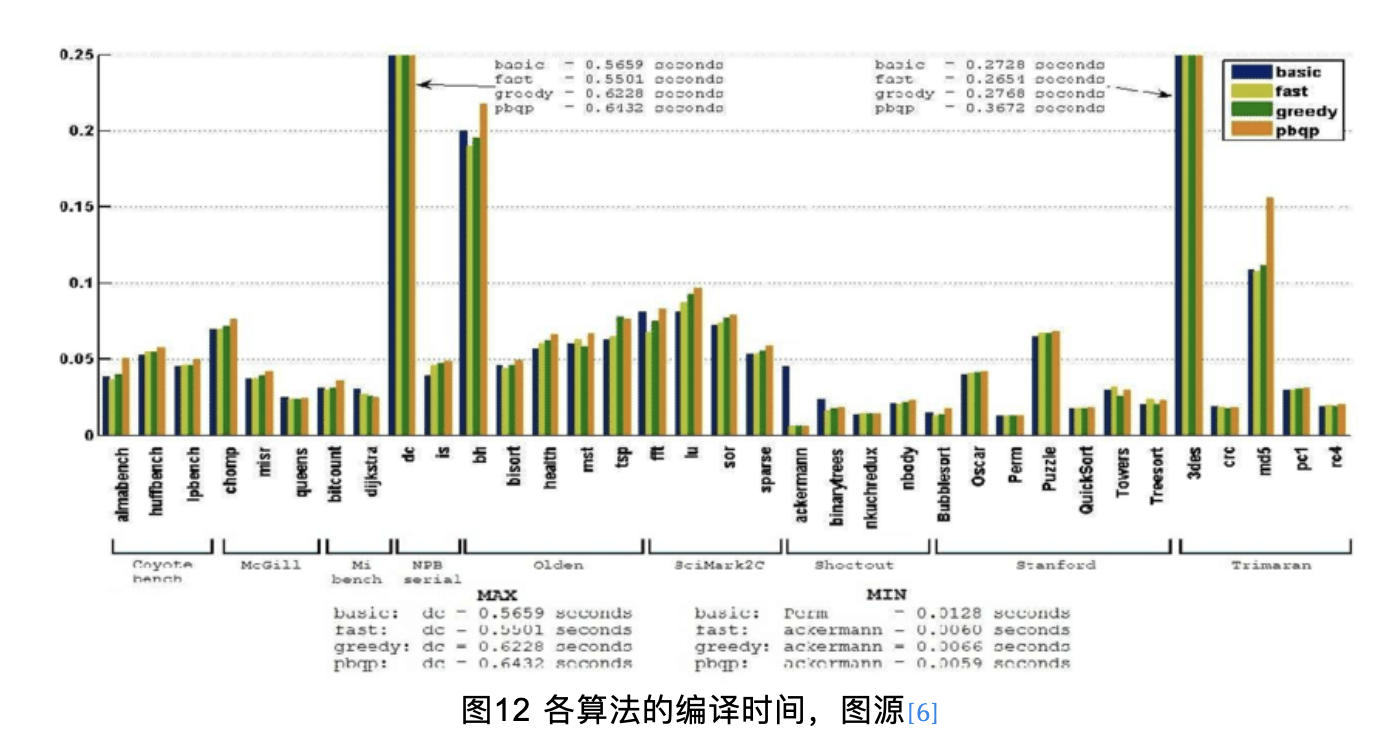
横坐标是测试集,纵坐标是编译时间
从这三幅图可以看出greedy算法在大多数测试集上都优于其他算法,因此greedy作为默认分配器是可行的。
小结
我们通过一个例子介绍了活跃变量分析和图着色算法。借助活跃变量分析,我们知道了变量的生命期,有了变量生命期建立干涉图,对干涉图进行着色。如果着色失败,可以选择某个变量溢出到内存中。之后在RIG的基础上介绍了寄存器合并这一变换。
然后我们简单介绍了不同思路的寄存器分配算法:linearscan。最后介绍了llvm12中算法的实现并对比了llvm中四种算法的性能差异。
作者:王博洋
文章来源:毕昇编译
推荐阅读
欢迎大家点赞留言,更多Arm技术文章动态请关注极术社区嵌入式客栈专栏欢迎添加极术小姐姐微信(id:aijishu20)加入技术交流群,请备注研究方向。