AI加速器 Kernel Computation 计算优化方式

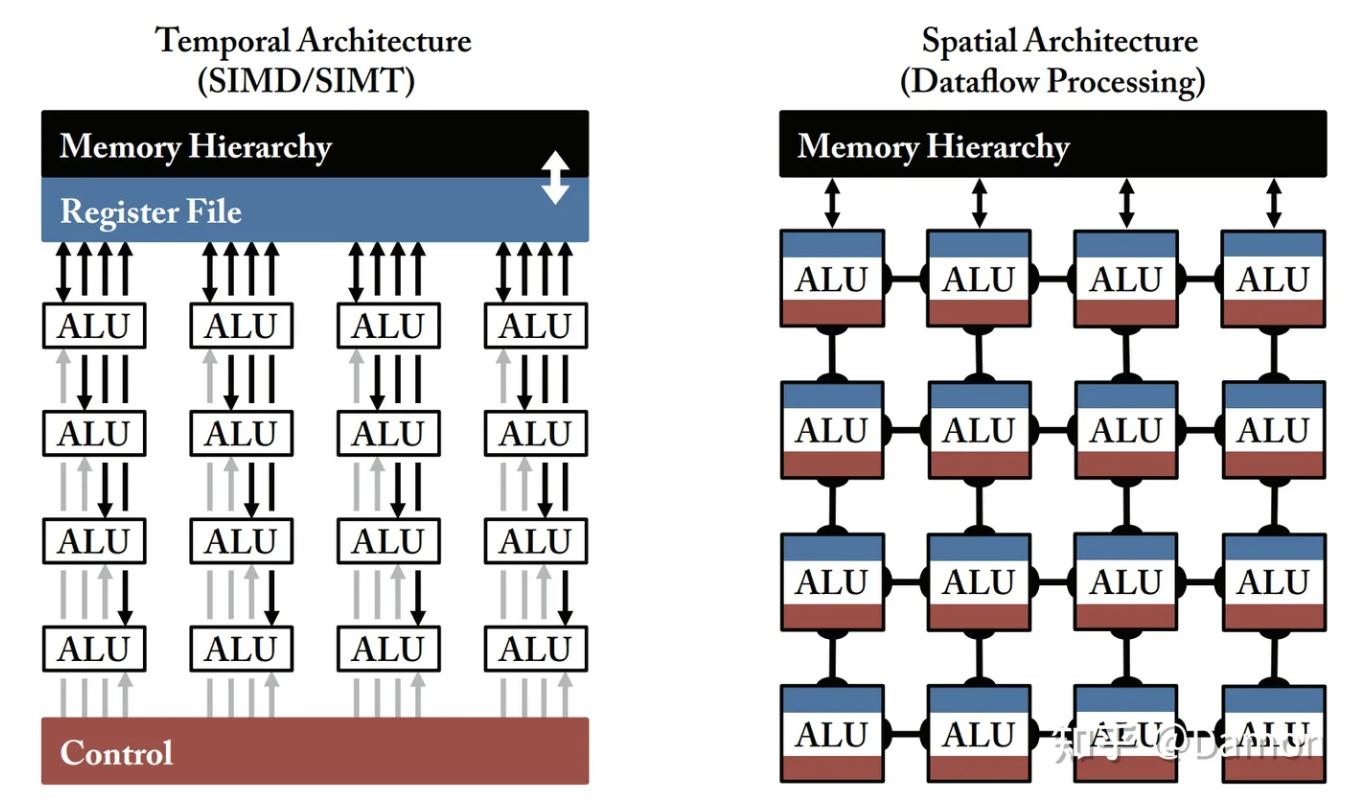
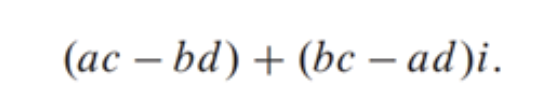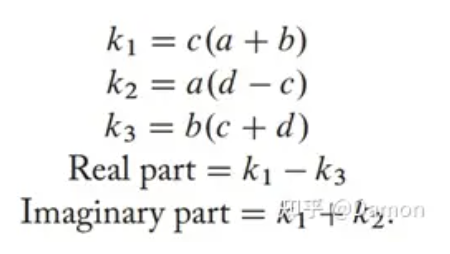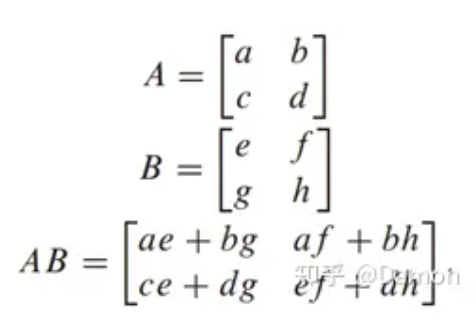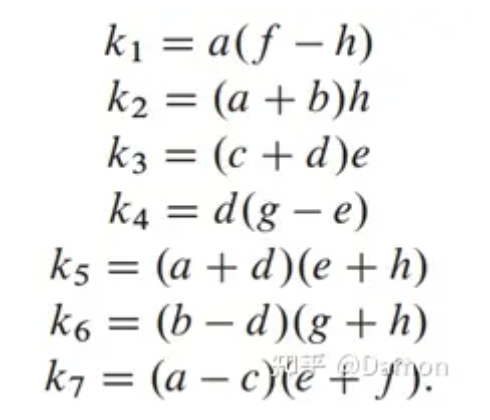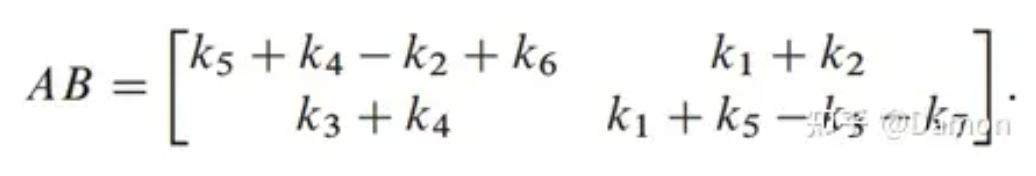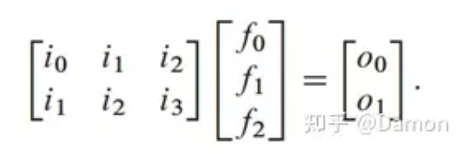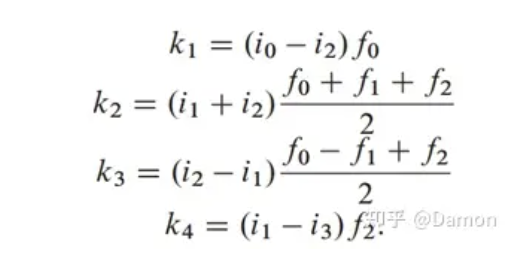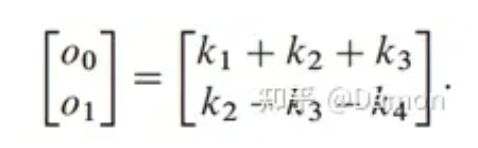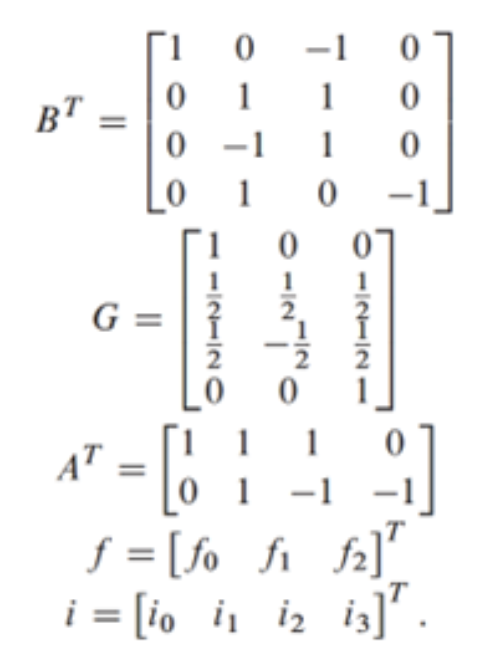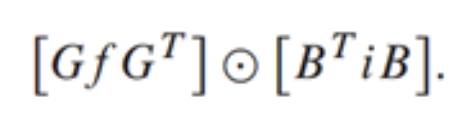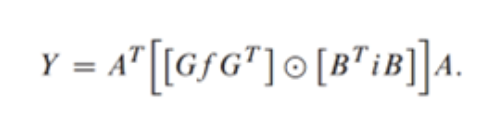第2章描述的CONV层和FC层的基本计算都是乘法累加(MAC)操作。因为这些操作之间的依赖关系可以忽略不计，而且累积是可交换的，所以在调度MAC的顺序上有相当大的灵活性，并且这些计算可以很容易地并行化。因此，为了实现深度神经网络的高性能，高度并行计算范式被广泛使用。这些架构范例可以分为时间的或空间的，如图4.1所示。

图4.1 高度并行计算示意

时序体系结构对大量算术逻辑单元(ALU)中控制。这些ALU通常只能从内存层次中获取数据，不能直接相互通信。这种架构主要出现在CPU或GPU中，采用各种技术来提高并行性，如向量指令(例如SIMD)或并行线程(例如SIMT)。相比之下，空间体系结构允许ALU之间通信，并使用数据流处理(即ALU形成一个处理链，以便它们可以直接在彼此之间传递数据)。有时每个ALU可以有自己的控制逻辑和local memory，称为scratchpad或register file。我们把有local memory的ALU称为处理引擎(processing engine, PE)。在基于ASIC和FPGA的设计中，空间架构通常用于处理深度神经网络。

随着DNN的普及，许多可编程时态系统(即CPU和GPU)开始添加针对DNN处理的feature。例如，英特尔Knights Landing CPU具有用于深度学习的特殊向量指令，可执行多次融合乘累加操作；Nvidia PASCAL GP100 GPU支持16位浮点(fp16)计算，可以在单个精度核心上执行两个fp16操作，以更快地进行深度学习计算。如4.1节所述，DNN计算通常可以转换为矩阵乘法。因此，Nvidia VOLTA GV100 GPU提供了一个特殊的计算单元，用于执行矩阵乘法和累加。该单元上的活动由执行许多MAC操作的单个指令调用。

我们还看到了专门为DNN处理而构建的系统，如Facebook的Big Basin自定义DNN服务器[125]和Nvidia的DGX-1。DNN模型推理也逐渐的出现在端侧设备的SOC上，如苹果的处理器，nvidia的Tegra以及高通、MTK、三星的Exynos等手机芯片。

在本章和第5章中，我们将讨论在这些不同平台上进行高效处理的不同设计策略，同时不会对accuracy产生任何影响（即，本章中的所有方法都会产生逐位相同的结果），尤其是：

对于诸如CPU和GPU这样的时序体系结构，我们将讨论如何在这些平台上映射和优化DNN算法，如何在内核上进行计算转换以减少乘法数量以提高吞吐量，以及如何对计算(例如MAC)进行排序(即平摊)以改善内存子系统的行为(本章)；
对于AI加速器中使用的空间架构，我们将讨论数据流如何提高内存中的数据重用以降低能耗，以及其他架构特性如何帮助优化数据移动(第5章)。

4.1 用Toeplitz进行矩阵乘法

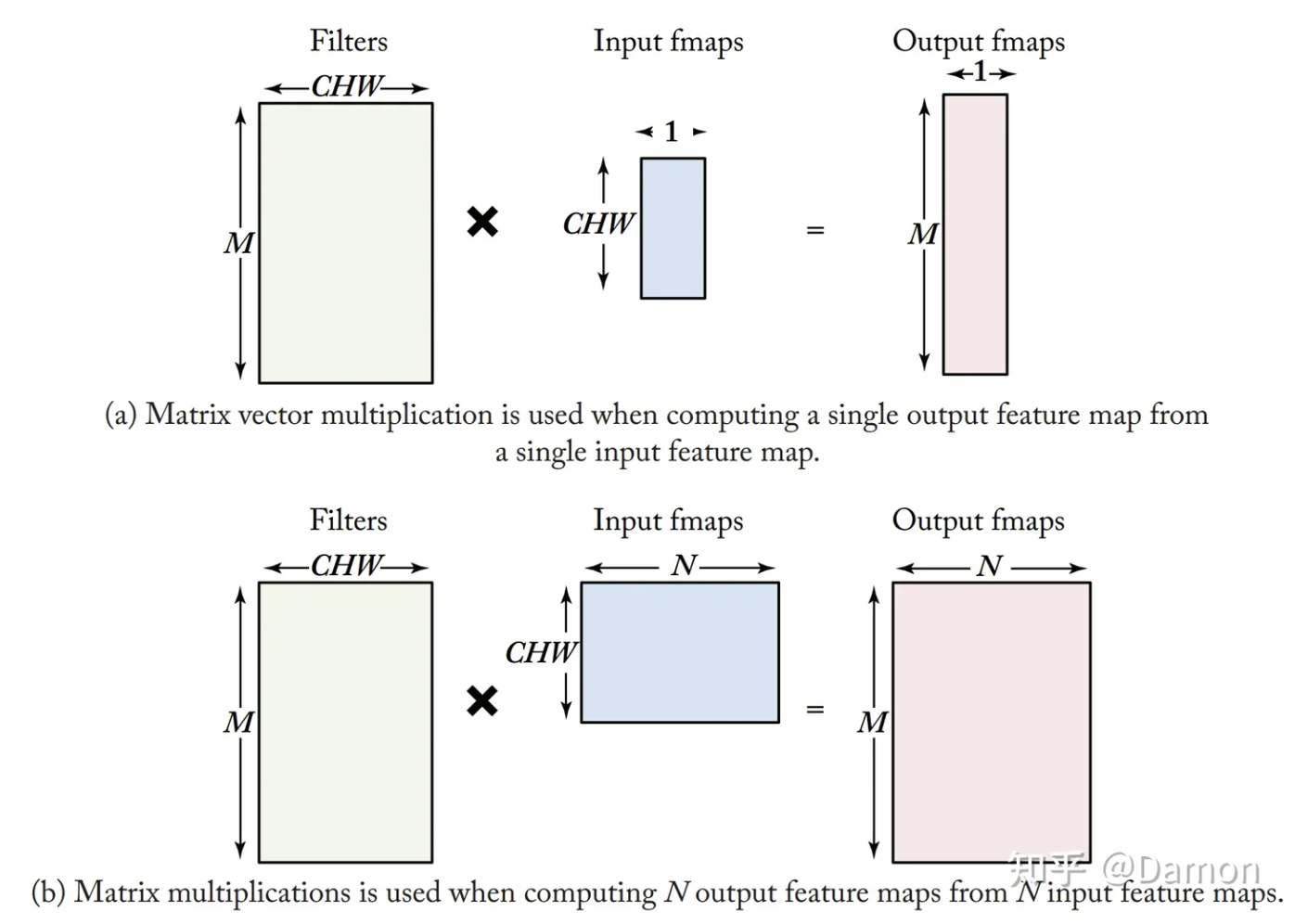
CPU和GPU使用硬件并行化技术(如SIMD或SIMT)并行执行MAC。所有ALU共享相同的控制和内存(register file)。这样的方案自然适合于执行matrix-matrix或matrix-vector乘法中的许多常规并行乘法，因此，FC layer和CONV layer的kernel计算通常映射为矩阵乘法。图4-2展示了如何在FC layer使用矩阵乘法。Filter matrix的height是3-D filter的数量 (M)，宽度是每个 3-D 滤波器的权重数量（输入通道(C) 高度(H) 宽度(W )，因为滤波器高度 ( FC层中R)等于H，滤波器宽度(S)等于W)；输入特征图矩阵的高度是每个3-D输入特征图(CHW)的激活数，宽度是3-D输入特征图的数量，也称为batch size(图 4.2a 中为 1，图 4.2b 中为 N)；最后，输出特征图矩阵的高度是输出特征图中的通道数(M)，宽度是3-D输出特征图的数量/batch size (N)，其中FC层的每个输出特征图的维度为11个输出通道数(M)。

图4.2 映射到FC层的矩阵乘法(其中filter大小等于输入特征映射大小，如R=H和S=W);换句话说，图中的CHW与CRS相同。当batch size的N=1时，结果为matrix-vector乘法，而当batch size的N>1时)结果为matrix-matrix乘法。

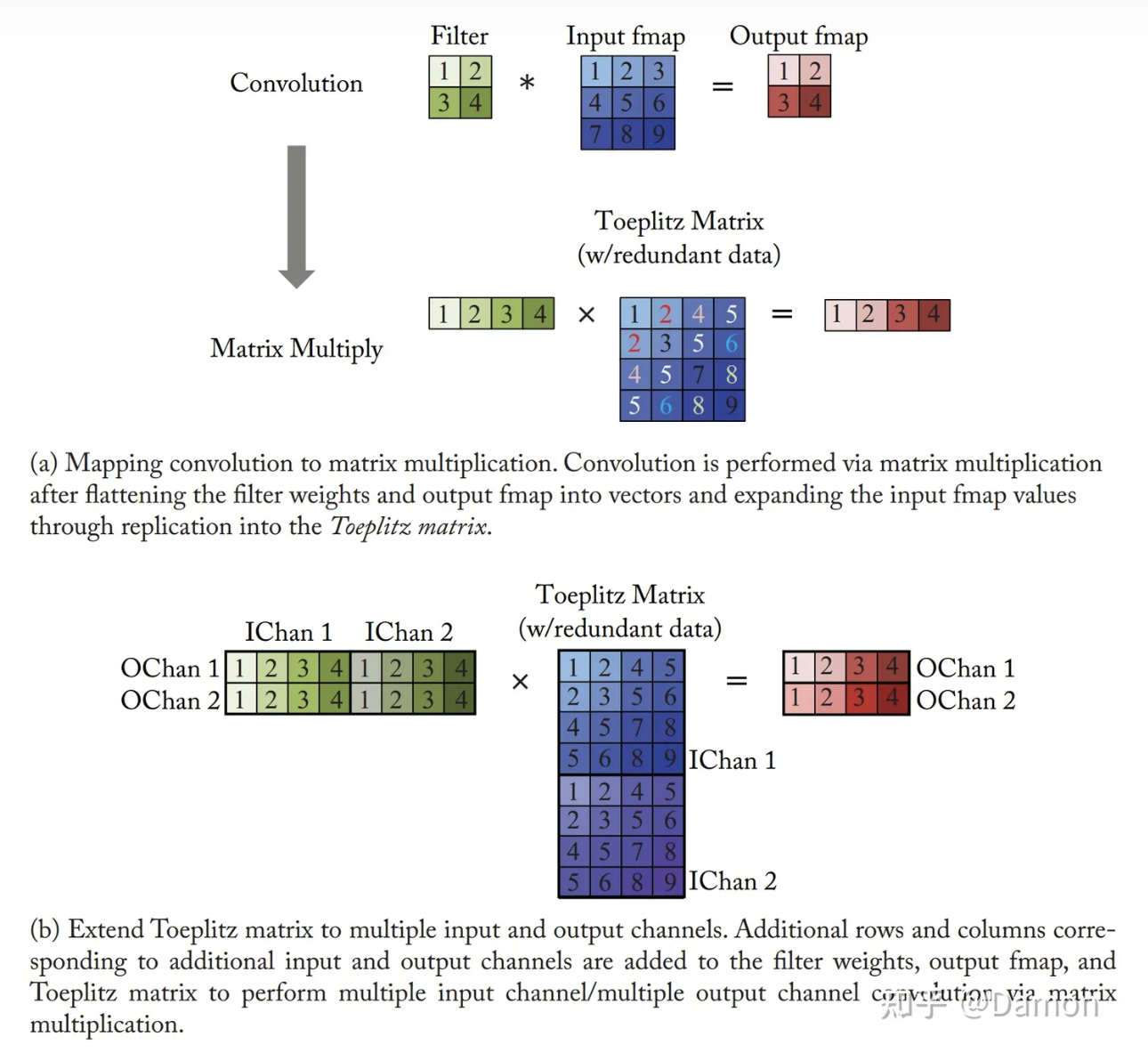
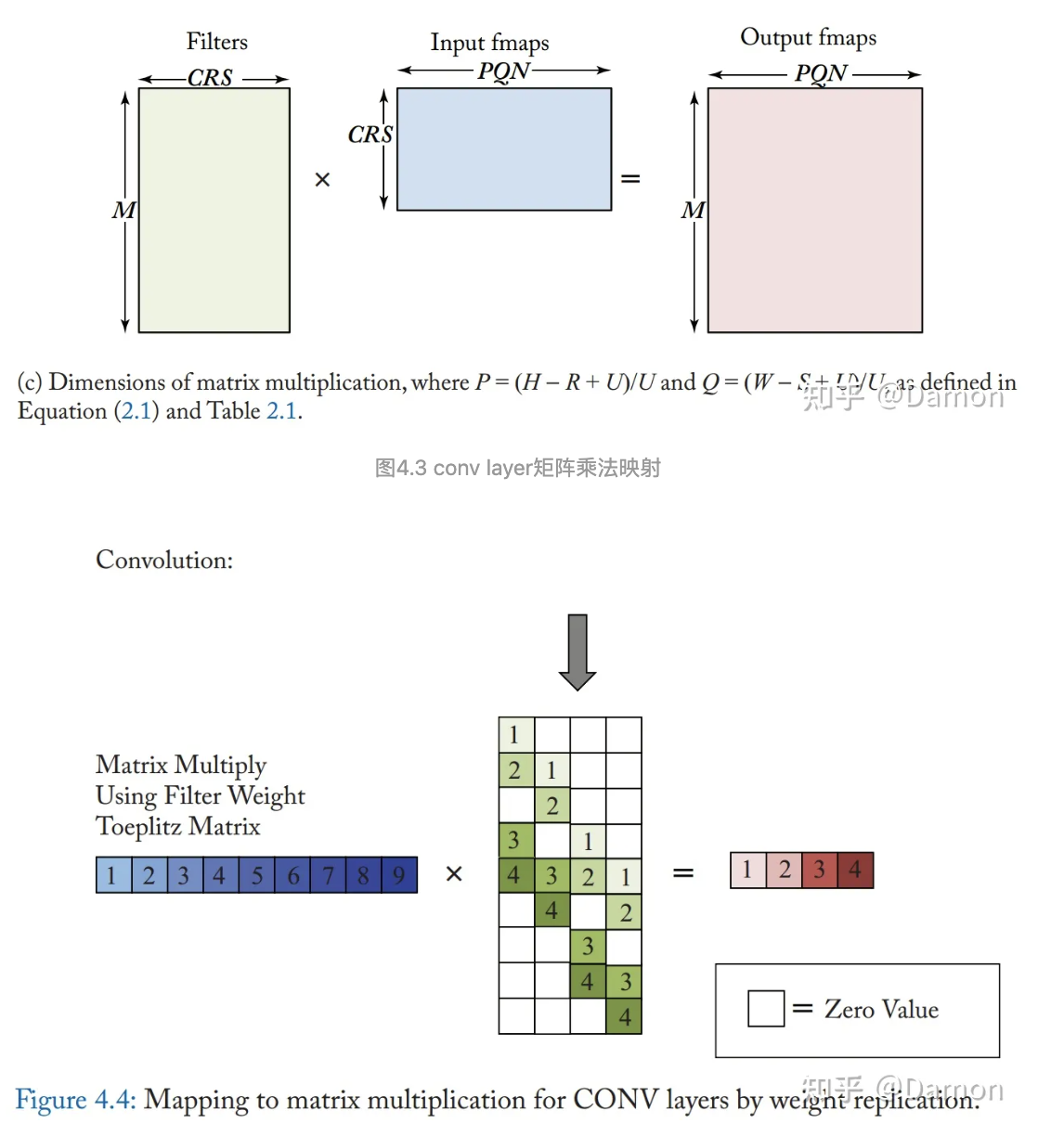
DNN中的卷积层也可以映射为使用松弛形式的Toeplitz矩阵进行矩阵乘法，如图4-3所示。在这种形式中，输入特征映射中的输入激活被复制，以对应于输入激活卷积的重用。对CONV层使用矩阵乘法的缺点是在输入特征映射矩阵中有冗余数据，如图4-3a所示。这要么导致存储效率低下，要么导致复杂的内存访问模式。

图4.4 通过权值复制映射到CONV层的矩阵乘法

4.2 Tiling 性能优化

如前一节所述，许多DNN计算可以表述为矩阵乘法。为了有效地执行这些计算，有许多为CPU(例如，OpenBLAS, Intel MKL等)和GPU(例如，cuBLAS, cuDNN等)设计的软件库，它们优化了矩阵乘法的实现。这些库的一个关键特征是它们努力优化内存子系统的行为。具体来说，考虑到传统的内存子系统组织将越来越小、更快和更低能耗的内存放置在靠近计算单元的地方，库试图最大限度地重用保存在更小、更快、更节能的内存中的值。

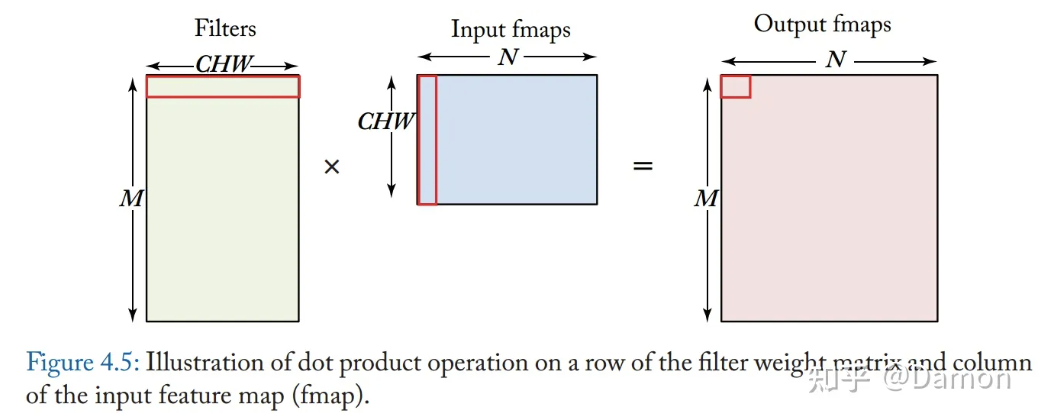
为了理解如何最大限度地重用离计算单元最近的内存中的值，请考虑一个在全连接计算中使用的矩阵乘法的简单实现，如图4-5所示。该图显示了滤波器权重矩阵的行如何与输入特征图的列相结合。这种组合涉及对来自过filter行的值和input fmaps列的值进行元素相乘，以及对结果向量的所有元素进行最终求和(即进行内积)。每个这样的内积产生输出特征映射矩阵中一个元素的值。这种计算风格被称为矩阵乘法的内积(inner product)方法。

图4.5 输入特征映射(fmap)的滤波器weight矩阵的一行与列的点积运算说明

如果内积计算是有序的，使得滤波器矩阵的一行与输入特征映射的每一列依次组合，那么显然可以很好地重用滤波器矩阵的行元素。然而，filter矩阵的一行通常需要比较大的存储空间，而最靠近计算单元的buffer通常小于这个值，因此weight的值无法保存足够长的时间，从而无法通过对input fmap的下一列进行计算来重用他们，必须从内存层次的下一层重新加载weight行值，这就会导致计算效率显著降低。

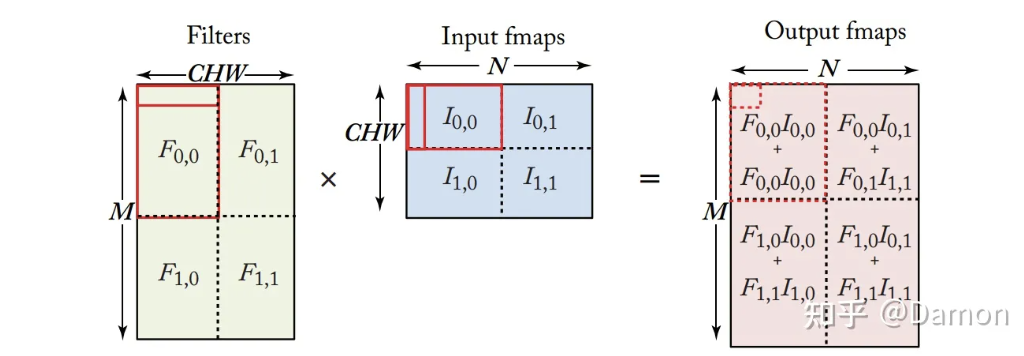
为了改善由于一次性计算矩阵乘法的全部行和列的内积而导致的内存效率低下，库总是将计算做partition或tile以适应存储层次的不同层次。tiling背后的原理如图4-6所示，其中的内积是对整个矩阵进行2-D partition(或称tile)。对于矩阵中的每一对tile，可以对输入特征映射矩阵中的滤波器权重的部分行和部分列采用相同的内积方法，以在输出特征映射中创建部分结果的tile。随着对所有图像tiles的计算完成，后续的部分结果将添加到输出特征图中先前部分结果计算的部分结果中。如果重复使用单个过滤器权重块来创建一系列的局部结果，并且如果该tile足够小，可以保存在离计算单元最近的内存中，那么该内存中的重用率将会更高。

矩阵乘法的tile可以递归地应用，以提高存储层次的每一层的效率。tile也可以应用于跨多个CPU或GPU的多个线程的并行计算。因此，通过根据存储层次中每一层缓存的大小和并行计算单元的拓扑结构等特征，为每个相匹配的体系结构适当地分配计算，对用于矩阵乘法的CPU和GPU库进行了优化。

图4.6 滤波器weight矩阵的平铺行和输入特征映射(fmap)的平铺列上的点积运算的插图。请注意，输出用虚线突出显示，因为只计算了部分值(来自图块F0,0和I0,0)。为了完成输出的计算，需要对tiles F0,0和I0,0执行点积操作，并与之前的结果进行累积。

tiling算法要求相当复杂。例如，由于集合关联缓存有一个策略来确定在需要添加新数据时（即缓存未命中时）保留哪些数据，因此会出现额外的复杂性。这些策略是通过复杂的基于硬件的替换算法实现的(例如，最近最少使用(LRU)或动态重新引用间隔预测(DRRIP)[126])。因此，库还必须尝试准确地考虑如何保留tiles以实现最佳性能。为了处理各种各样的硬件平台和layer shape，这些库通常具有针对特定硬件平台和layer shape进行优化的算法的不同实现，例如矩阵乘法。这种优化总是包括平铺策略。因此，当调用库时，它将动态选择并运行最合适的实现。

除了现有的库可以动态地从实现菜单中选择外，还在编译器上进行了大量工作，以优化用户编写的分块程序，例如，[127]。这项工作的一部分依赖于创建计算的多面体模型，并使用布尔可满足性(SAT)求解器来优化平铺和调度程序[128]。这些技术已经被添加到流行的GCC和LLVM编译器框架中。Halide[129]是另一种方法的例子，它将算法的基本表达式与用户提供的描述所需调度和算法分块的注释解耦。TVM[130]是一个编译器，它为不同的硬件后端提供了DNN工作负载的graph-level和operator-level优化。除了tiling以隐藏内存延迟外，TVM还执行诸如高级算子融合(例如，在一次通过内存的情况下执行CONV层和ReLU)以及映射到任意硬件原语的优化。

第5章将讨论tiling的概念，tiling的概念也适用于执行矩阵乘法或直接执行卷积的特定DNN架构。在这样的体系结构中，tiling也是为了最大化内存层次和并行计算单元中的数据重用。但是，tiling不是在缓存(即隐式数据编排单元)中完成的，而是在更专门的缓冲区(即显式数据编排单元)中完成的，后者的数据保持特征更直接地由程序控制，这些会在5.8节中描述。

（待更新）

4.3 计算转换优化

网络模型的一些计算有时候可以通过计算形式的转换来减少乘法的次数，同时仍然提供相同的按位结果。目标是提高性能或减少能耗，尽管这可能会引起更多的中间结果需要缓存、更多的额外数据和更不规则的数据访问模式。

4.3.1 Gauss 复杂乘法变换

可以把这些变换看作是高斯复数相乘的更复杂版本。在复数乘法的标准方法中，计算(a+ bi)(c + di)是通过一系列交叉项乘法来完成的，如下所示:

在这个例子中，计算需要4次乘法和3次加法。不过，我们可以将上述操作重新关联起来，计算3个中间项，然后通过中间项的和与差(kj)计算结果的实部和虚部，如下所示:

在变换后的形式中，计算简化为3次乘法和5次加法。在以下几节中，我们将讨论更复杂的矩阵乘法和直接卷积计算的重新关联，这些计算可以减少乘法的数量。

4.3.2 Strassen 矩阵乘法变换

对于矩阵乘法，一个著名的变换方法是Strassen算法，该算法已被探索用于减少DNNs中的乘法数量[131]。Strassen算法用递归的方式重新排列矩阵乘法的计算，将乘法的次数从O(N^3)减少到O(N^2.807)。Strassen算法在2x2矩阵乘法上的应用示例如下:

在这个例子中，8次乘法和4次加法被转换为7次乘法和18次加法，并创建了7个中间值(kj):

最终输出AB由中间值(ki)构成，如下所示:

注意，当用于DNN计算时，其中一个矩阵将包含filter weight，该权重在不同的输入中是恒定的。在这个例子中，使用常数B矩阵进行预计算，将加法次数减少到13次。总之，Strassen可用于减少乘法次数，但其好处是以增加中间结果的存储需求为代价的，有时还会降低数值稳定性[132]。此外，对于比DNN中通常使用的矩阵更大的矩阵，Strassen的好处主要表现出来。

4.3.3 Winograd 变换

Winograd的算法[133,134]对特征映射和过滤器应用算术操作的重新关联，以减少卷积所需的乘法数量，而不是由之前描述的转换处理的通用矩阵乘法。

Winograd变换允许使用相同的滤波器权重高效地计算多个卷积。例如，计算两个输入激活(ij)和滤波器权重(fj)的1x3卷积，通常需要6次乘法和4次加法，如下所示:

然而，使用Winograd重新关联，这减少到使用4个中间值（kj）的4次乘法和12次加法以及2次移位（以实现除以2），如下所示：

最终输出（oj）由中间值（ki）构成，如下所示：

使用恒定的滤波器权重，这将减少到4次乘法和8次加法。需要注意的是，每个Winograd转换应用只对少量输入激活(即输入激活的tile)进行卷积。因此，为一个输入特征图做整个卷积集需要在tile by tile的基础上应用Winograd；所以需要使用输入激活的滑动窗口生成一系列独立的输出tile (即，输入在输出tile中重用)。Winograd变换可以通过重复应用变换应用于2-D卷积。

Winograd实现的乘法减少程度取决于滤波器和tile大小。更大的tile可以在更大程度上减少乘法，但代价是更高的变换复杂度。常用的filter尺寸是3x3，在计算一个2x2输出大小的tile时，可以减少2.25x乘法。注意Winograd需要根据tile和filter的大小进行特殊处理，因此Winograd硬件通常只支持特定大小的tile和filter，例如nvidia只支持3x3filter。

Winograd的矩阵线性代数公式如下所示：

在这个公式中，计算的第一步是变换filter weight (fj)和输入激活(ij)，，通过将这些矩阵分别夹在常数矩阵GfGT和BTiB的矩阵乘法链中。得到的值可以被认为存在于“Winograd”空间中，在该空间中，可以通过将这些矩阵与计算高效的逐元素乘法相结合来执行卷积，如下所示:

最后，“Winograd”空间的反向变换是通过再次将元素乘法的结果夹在常数矩阵AT和A的矩阵乘法链中来执行的。

4.3.4 快速傅立叶变换

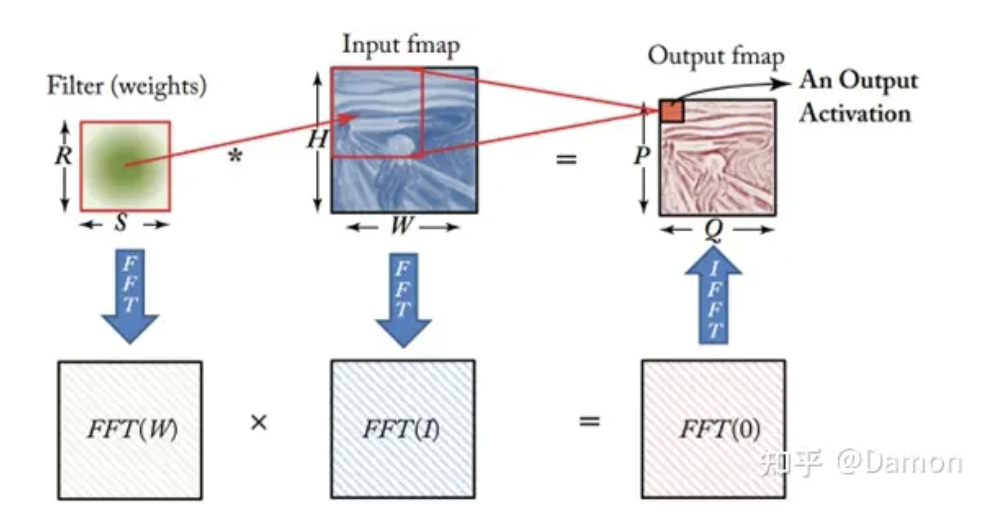
快速傅里叶变换(FFT)[19,136]遵循与Winograd变换相似的模式，将卷积转换为新的空间，使得卷积的计算效率更高。如图4.7所示，将每个输入通道的乘法次数从O(RSPQ)减少到O(PQlog2PQ)，其中输出大小为PxQ，filter大小为RxS。为了执行卷积，我们取filter和输入特征映射的FFT，然后在频域中执行element-wise乘法；然后对结果乘积应用逆FFT以恢复空间域中的输出特征映射。然而，使用FFT有几个缺点：(1)FFT的好处随着filter的大小而减少（取决于filter大小RxS和输出大小PxQ之间的比率。在考虑了常数项之后，需要RS>log2PQ才能有优势）；(2) FFT的大小取决于输出特征映射的大小，通常比filter大得多;(3)频域系数为复系数。因此，虽然FFT减少了计算，但它需要更大的存储容量和带宽。而降低复杂性的一种常用方法是使权重稀疏，这将在8.1.2节中讨论；使用FFT使得这种稀疏性很难被利用。

图4.7: FFT to accelerate DNN

可以对FFT进行一些优化使其对DNN更有效。为了减少运算次数，可以预先计算并存储filter的FFT。此外，输入特征图的FFT可以计算一次，并用于在输出特征图中生成多个通道。由于图像只包含实数，其傅里叶变换是对称的，这可以用来减少存储和计算成本。

4.3.5 选择一种变换方式

在实践中，不同的算法可能用于不同的图层形状和大小(例如，FFT用于大于5x5的filter，Winograd用于filter3x3及以下)。现有的平台库，如MKL和cuDNN，可以针对给定的形状和大小动态选择合适的算法[138,139]。

4.4 总结

在本章中讨论了在CPU/GPU等平台上实现高效运算处理的不同方法。目标是重构计算以提高效率而不影响精度(本章中的所有方法都产生接近按位相同的结果)。这些方法的目标是减少内存带宽(例如tiling)；重塑计算以提高效率；或者减少高成本操作。重塑计算的一个重要例子是Toeplitz变换，它被广泛应用于CPU/GPU。Toeplitz变换通过复制值将卷积转换为矩阵乘法，这允许应用任何高度优化的矩阵乘法库中的例程。最后，各种其他转换旨在通过代数重新关联减少高成本操作(即乘法)的数量，包括Strassen, Winograd和FFT转换。

作者：Damon
文章来源：知乎

更多嵌入式AI干货请关注嵌入式AI专栏。欢迎添加极术小姐姐微信（id:aijishu20)加入技术交流群，请备注研究方向。